一种用于短猝发通信的LDPC短码设计

陈远友

(中国电子科技集团公司第五十四研究所，河北石家庄050081)

0 引言

LDPC码是Gallager在1962年提出的利用稀疏校验矩阵的信道编码方案［1］，是一种可以接近Shannon限的“非常好”的分组码［2］，为了追求优异的性能，采用随机化方法构造的校验矩阵［1－3］使得编码器的设计十分困难，译码器的存储复杂度也高，实现困难。为了构造易于实现、性能优良的编码方法，人们提出了很多改进方法［4－11］，针对具体应用的文献也很多［12－15］。

一般来说，码字长度越长，LDPC的编码性能越好，因此，通常设计的LDPC的码字都较长，达到数千位。但在某些应用场合，如在短猝发隐蔽通信中，由于通信时间非常短，数据量较少，不可能采用码字较长的编码方案，必须设计针对这种特殊应用场合的短码。

1 LDPC短码设计

1.1 LDPC码的构造方法

准循环LDPC(quasi-cyclic LDPC)码是一种可以使用简单移位寄存器实现的结构化LDPC码，精心设计的准循环LDPC码在比特差错率、块差错率以及差错平底等方面可以达到计算机随机构造码的性能。

在给定长度和度分布对的情况下，通过随机连接二分图的变量节点和校验节点，就可以得到一个随机LDPC码集。由于LDPC码主要采用置信度传播(BP)迭代译码算法，在无短环情况下才能获得最佳性能。就长码而言，码集平均性能随码长增加，码集中的单个码性能趋近于平均性能。而对于短码，因为码长有限，二分图中的短环明显增多，特别容易出现四环，导致有限次迭代之后软信息出现相关，算法无法收敛或收敛速度减慢，造成性能下降。为此需要通过调整校验矩阵中环的分布情况，避免出现四和六环，增大短环的围长［9］，从而构造性能较好的LDPC码字。

1.2 PEG构造方法

PEG(Progressive Edge-Growth)［4］是随机构造LDPC码的一种相对简单但有效的算法，它按某种规则逐步向Tanner图添加连接变量节点和校验节点的边，选择合适的规则使Tanner图中的环最大。仿真显示使用PEG算法构造的短码长LDPC码比随机构造的码字有很大的性能提升［5］。

PEG算法通过展开Tanner图，按照逐节点的方式在校验节点和变量节点之间建立边的连接，在增加新边时尽可能减少对已有Tanner图围长的影响，充分考虑使Tanner图的围长达到最大以避免短环的存在，最终获得性能较好的LDPC码。

对给定的双向图参数，包括变量节点数N、校验节点数M、变量节点度序列Dv，常规PEG算法如下［4］:

令第i个变量节点为vi，第j个校验节点为cj;

对于第i个变量节点:i=0到 N－1;

增加第i个变量节点的第k条边:k=0到dvi－1;

其中，dvi表示第i个变量节点vi的度数。

如果 k=0，则边(vi，cj)→，其中是变量节点vi的第一条入射边，cj是在当前图集合Ev0∪Ev1∪…∪Evi－1中具有最低度数的校验节点之一。

否则，在当前图集合的基础上，将变量节点vi展开成深度为l的子图，直到集合的元素数目达到 M，或

然后，(vi，cj)→，其中是变量节点vi第k条入射的边，cj是集合中具有最低度数的校验节点。

第3步:对任意的若满足RSθ,η(Reduct{a},D)⟹RSθ,η(A,D),则转下一步;若中不存在a使得RSθ,η(Reduct{a},D)⟹RSθ,η(A,D),则算法结束,返回Reduct;

1.3 准循环短码设计

常规PEG算法需要对每一个变量节点都展开成树图结构，以逐点的次序添加边，这样不但耗费时间和内存资源，而且构造的矩阵也没有规律，给编译码的硬件实现带来困难。改进的QC-PEG-LDPC算法构造的准循环校验矩阵是由多个循环子矩阵构成，在构造时首先把变量节点和校验节点分成多个小组，然后对于每组变量节点，只需对其中第一个变量节点寻找最优边，最后根据循环矩阵的约束关系，同组其他节点相连的边也随之确定。

下面以构造一个码长为700，码率为3/7的准循环LDPC码字为例说明改进的PEG算法。

该准循环矩阵用HM×N表示，每个子矩阵用Ark表示，该校验矩阵的子矩阵维数为100×100，有28个循环子矩阵，M=b×c=100×4，N=b×t=100×7，0≤r＜c，0≤k＜t。矩阵的行重和列重分别为dc=5和dv=3，即校验节点的度为5，变量节点的度为3。

文献［9］专门研究了设计准循环LDPC码时如何避免短环问题与校验矩阵的行相关问题，提出了避免短环的准循环LDPC码的设计约束条件。

已证明构造的校验矩阵H所对应的LDPC码不包含长度为4的环的必要条件为［6］:

因此为了避免4环的出现，需要遍历准循环矩阵HM×N中的元素，对不满足条件的元素进行修正处理，使修正后的扩展矩阵中所有元素的值都小于LDPC码的扩展因子z。

2 性能仿真与测试

为了定量分析所设计的短码性能，以 LDPC(700，300)为例对其进行了性能仿真，并在通用调制解调器硬件平台上进行了性能测试。

2.1 性能仿真

仿真条件:

译码方式:修正最小和译码算法;迭代次数:50次;

信道条件:高斯白噪声，编码环。

如图1所示，仿真结果显示，基于QC-PEG-LDPC算法构造的准循环LDPC码性能优良，在归一化最小和译码算法下，Eb/N0值为 2.9 dB，BER≤10－5。且因为其具有准循环结构，译码器结构简单，便于硬件实现。

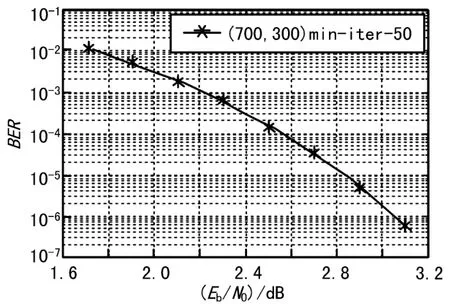
图1 LDPC(700，300)编码环仿真误码曲线

2.2 性能测试

测试条件:

信息帧长:300 bit;

LDPC(700，300):码率 3/7;

猝发调制方式:BPSK+扩频;

译码方式:修正最小和译码算法;

迭代次数:50次;

信道条件:高斯白噪声，中频环。

硬件资源需求情况如下:

逻辑单元:10 280;

寄存器:16 224;

存储器:1 693 234;

乘法器:71。

占用资源较少，具有很好的可实现性。

测试结果如图2所示，由此可见，Eb/N0值为4.3 dB，BER≤10－5。

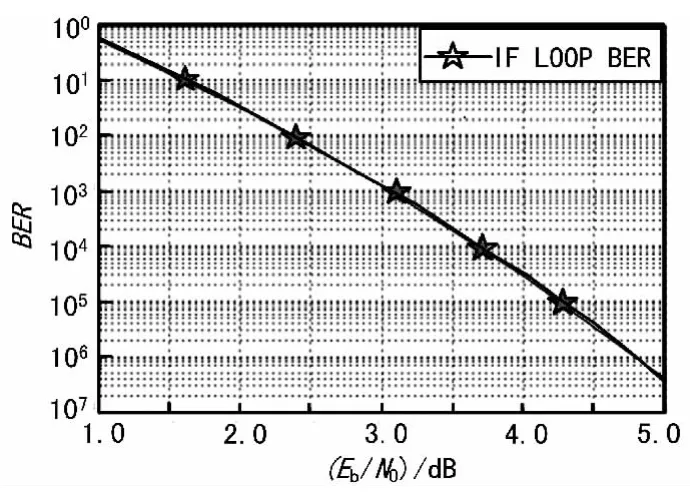
图2 LDPC(700，300)中频环测试误码曲线

3 结束语

针对短猝发隐蔽通信的通信时间非常短、数据量较少但对数据传输可靠性要求又很高的需求，提出了采用改进的PEG方法构建准循环LDPC短码的方法，计算机仿真和电路性能测试表明，构造的短码具有优良的性能，并且其电路实现复杂度较低，占用硬件资源较少，译码延时较小，便于工程实现。

［1］GALLAGER R G.Low Density Parity Check Codes［J］.IRETrans.Inf.Theory，1962，8(1)：21 － 28.

［2］MACKAY D J C.Good Error-correcting Codes Based on Very Sparse Matrices［J］.IEEE Trans.Inf.Theory，1999，45(2)：399 －431.

［3］PRABHAKAR A，NARAYANAN K.Pseudorandom Construction of Low-density Parity-check Codes Using Linear Congruential sequences［J］.IEEE Trans.on Commun.，2002，50(9)：1389 －1396.

［4］HU X Y，ELEFTHERIOU E，ARNOLD D M.Progressive Edge Growth Tanner Graphs［C］∥San Antonio，TX：GLOBECOM.01.IEEE，2001：995 －1001.

［5］HU X Y，ELEFTHERIOU E，ARNOLD D M.Regular and Irregular Progressive Edge-growth Tanner Graphs［J］.IEEE Trans.Inf.Theory，2005，51(1)：386 －398.

［6］傅婷婷，吴湛击，王文博.基于PEG算法的准循环LDPC码的编码构造方法［J］.数据采集与处理，2009(B10)：182 －186.

［7］敬龙江.低密度校验码的构造和设计研究［D］.成都：电子科技大学，2007：25 －85.

［8］焦治克.删除信道下的LDPC码与PEG算法研究［D］.西安：西安电子科技大学，2008：37 －59.

［9］肖扬，徐丹.准循环LDPC好码设计［J］.系统工程与电子技术，2009，31(5)：1011 －1017.

［10］范俊，肖扬.可快速编码的准循环LDPC码设计［J］.应用科学学报，2010，28(1)：1 －8.

［11］王启玮，战兴群，严凯.LDPC码的编译码设计与研究［J］.计算机测量与控制，2013，21(3)：728 －731.

［12］李志勇，李文铎.一种高速LDPC编译码器的设计与实现［J］.无线电工程，2009，39(7)：17 －19.

［13］刘波，李旭东.LDPC码在深空探测中的应用［J］.无线电工程，2009，39(10)：13 －15.

［14］魏瑞刚，陈晖，邱金蕙，等.高速数据传输中的LDPC码译码算法研究［J］.无线电工程，2011，41(3)：20 －22.

［15］赵建功，刘香玲.准循环LDPC码的部分并行译码算法［J］.无线电工程，2012，42(2)：55 －57.