基于QR分解的MIMO-OFDM检测算法的改进

陈 磊，张 敏，赵瑞弟，王可霞

（辽宁工业大学电子与信息工程学院，辽宁锦州121001）

0 引言

随着信息技术的发展，越来越多地需要高速率数据传输，无线通信技术也开始不断地向宽带无线传输方向转变，而MIMO技术[1]和OFDM技术[2]也已成为宽带无线传输的2个主体。将这2种技术结合的MIMO-OFDM系统可以实现很高的传输速率，并且能通过分集实现很强的可靠性，将会成为第4代通信发展的趋势。MIMO-OFDM系统信号检测算法的研究主要是在提高检测器性能和降低检测复杂度之间平衡。

1 系统模型

MIMO-OFDM系统[3]模型如图1所示。发射天线数为N，接收天线数为M。在发射机中，信源输出经串并变换和映射等处理后，形成N层并行数据流，每层数据再串并变换，然后进行IFFT，再经过并串变换和加循环前缀后送入发射天线，发射信号经频率选择性多径衰落信道到达M个接收天线，在接收端对各接收信号先去循环前缀，再经串并变换和FFT[4]等相反操作后将信号送入检测器检测并输出。

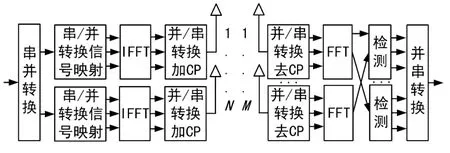
图1 MIMO-OFDM系统模型

接收机收到的信号矢量为:

式中，X=[X1…XN]T，Y=[Y1…YM]T和W=[W1…WM]T分别为发送信号矢量、接收信号矢量和高斯白噪声;H=[Hmn]为复数域上M×N矩阵，Hmn（n=1，…，N，m=1，…，M）表示从发射天线n到接收天线m间的信道频响系数。

2 基本算法原理

2.1 最大似然（ML）检测算法

最大似然检测算法[5]是最佳检测算法，其基本思想是:在所有可能的发送信号矢量集中遍历搜索，得到使似然函数最大的信号向量，将其作为估计。假设所有的未编码符号都是等概率发送的，那么ML检测算法为:

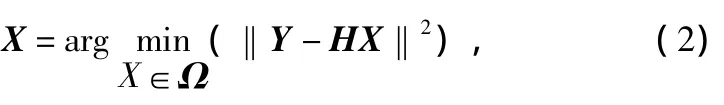
式中，Ω表示所有可能的发送信号矢量;‖Y－HX‖表示它的欧式距离。

2.2 迫零（ZF）检测算法

迫零检测算法的基本思想是:把信道矩阵H带来的干扰强制为零，所以被称作迫零算法[6]。它是空时信号处理接收算法中最简单的一个。ZF检测算法的加权矩阵为:

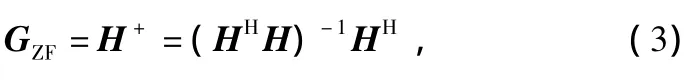
式中，（·）H表示矩阵的Hermitian矩阵;（·）+表示矩阵的广义逆矩阵。将加权矩阵GZF乘以式（1），可以得到:

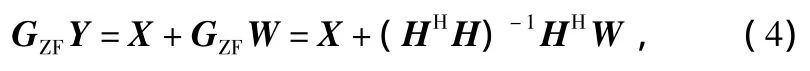
忽略噪声的影响，得到X的估计

2.3 最小均方误差（MMSE）检测算法

ZF检测算法在抑制信号干扰时忽略了噪声对系统性能的影响，而MMSE检测算法则不然。MMSE检测算法可使由噪声和同频信号相互干扰造成的错误达到最小。它虽然降低了信号分离的质量，但具有较好的抗噪性能。其基本思想是:使判决统计矢量和发送信号X之间的均方误差最小。MMSE检测算法的加权矩阵为:

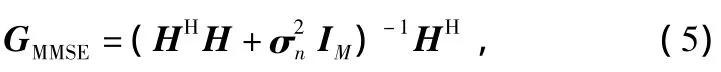
与式（1）相乘后得到:

2.4 串行干扰抵消（SIC）检测算法

干扰抵消算法是一个迭代过程。SIC检测算法[8]的思想是:采用一种复杂度不高的线性检测算法（ZF或MMSE），解调出一个天线上的数据，再消除解调出的符号在接收信号中对其他层的干扰，再用同样的方法，依次对其他天线上的发送符号进行线性检测和干扰抵消，直到估计出所有发送信号。

2.5 基本QR检测算法

将信道矩阵HN×M进行QR分解:

式中，QN×M是酉矩阵[9]，RM×M是一个上三角矩阵。通过将信道矩阵QR分解，得到接收向量的每一个分量，表示如下:

由于R具有上三角性质，因此可以从最底层开始得到各层发送信号的估计量，每层判决信号表示如下:

3 改进的QR算法

3.1 循环迭代QR算法

先对接收向量H进行一次QR分解，得到发射信号的估计向量。而最后检测层的分集增益最大，所以只判定输出性能最好的，其余各层的信息丢弃不用。接下来进行第2次检测，为了让第1次最后检测出的放到第1层检测，需要对信道矩阵H的列进行调整，然后再进行QR分解。因为检测时第1层的信息是第1次检测的结果，所以不用再判决。重复这个过程，直到检测出所有层的符号。循环迭代QR分解检测算法[10]的具体检测步骤如下:

①对H进行第1次QR分解，得到估计向量

③循环调整H的列向量:h1→hM→hM－1→…→h2→h1，即将第1列的向量移动到最后一列，其余各列依次往前移动一列。假设调整后新的信道矩阵为

④将进行QR分解并检测下面M－1层的信号，只保留最好检测层结果;

⑥通过新的检测，得到新的检测序列:

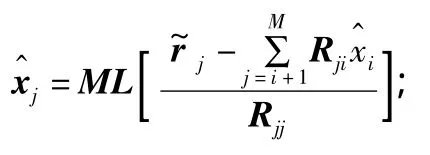
4发4收循环迭代QR检测的过程如表1所示。

表1 4发4收循环迭代QR检测过程

其中，H为信道增益矩阵;Y为接收端向量;X为发射端向量为第1次检测结果为最终检测结果。

3.2 IC_QR_LI算法

IC_QR_LI算法是在循环迭代QR检测算法的第1次QR算法之前先排序，无论是QR算法还是循环迭代QR算法，都有一个共同的缺点，就是有误差累计，即最先检测层产生的误差会影响到后续检测的准确度，现在在第1次QR分解之前先进行排序，使得在进行QR检测时最先检测层是信噪比最高的那一层，这样误差的累计就会有效地降低。本文只进行了一次排序，所以说算法复杂度几乎没有增加，而性能的提高相比于复杂度的增加却是相当可观的。

4 计算机仿真结果分析

仿真条件:MIMO系统的发送端天线数为4，接收端天线数也为4，收发均采用线性天线阵列，调制方式采用BPSK，收发之间存在理想的反馈信道。

采用循环迭代和不采用循环迭代的性能曲线如图2所示。采用循环迭代QR检测的性能比不采用循环迭代的性能要好很多。当然，性能的大幅提高也付出了算法复杂度增加的代价，4×4的MIMO系统采用循环迭代QR检测算法，要经过4次QR分解，复杂度是基本QR算法的4倍。采用预先排序和不采用预先排序的性能曲线如图3所示。采用了预先排序后检测的性能有了提高，而复杂度方面增加的运算量只有一次排序所需要的运算量。

图2 VBLAST系统QR检测算法采用循环迭代和不采用循环迭代的性能比较

图3 VBLAST系统QR检测算法采用排序和不采用排序的性能比较

5 结束语

提出了一种改进的QR检测算法，并利用MATLAB进行了仿真，比较了该算法与基本QR算法的性能。通过仿真可以看出，与基本QR算法和循环迭代QR检测算法相比，基于预先排序的循环迭代检测算法的性能是最好的，计算复杂度并没有增加很多，并且实现了检测性能和复杂度之间很好的平衡。

[1]GORVAJA R，ARMADA A G.Effect of Multipath and Antenna Diversity in MIMO-OFDM Systems with Imperfect Channel Estimation and Phase Noise Compensation[J].Physical Communication，2009，1（4）:288－297.

[2]胡茂凯，陈西宏，孙际哲，等.改进时变多径信道下OFDM系统性能分析[J].华中科技大学学报，2012，40（10）:2－3.

[3]饶文元，王军选.贝尔实验室分层空时结构和空时编码[J].电信快报，2004（3）:1－3.

[4]JIA Dan-ping，YUAN Zhuo，SAN Hong-li.The Study of Fluorescence Thermal Measurement Based on DSP [J].Procedia Engineering，2012，29:2864－2868.

[5]CHO Yongsoo，KIM Jaekwon，YANG Wonyoung，et al.MIMO－OFDM Wireless Communications with MATLAB[M].USA:John.Wiley ＆ Sons，2010.

[6]WANG Shi-liang，SUN Song-lin，JING Xiao-jun.Tree Pruning for MIMO Sphere Detection Based on MMSE Detection[J].The Journal of China Universities of Posts and Telecommunications，2012，19（4）:64－72.

[7]FENG Xing-le，ZHU Shi-hua，REN Pin-yi.Transmit Antenna Selection in V-BLAST System[J].Journal of Electronics，2005，23（4）:1－2.

[8]付翠竹.MIMO SIC检测合并技术[J].现代电信科技，2011（5）:1－2.

[9]CHENG Jing，HE Cheng-yuan.Some Properties of Generalized Unitary Matrices and Generalized Hermite Matrices[J].Journal of Chongqing Normal University，2010，27（3）:58－61.

[10]刘海涛，孙宇昊，李冬霞，等.基于QR分解的循环迭代检测算法[J].电波科学学报，2005，20（5）:2－3.