铁路既有线纵断面线形分段的优化算法

孟凡超，刘成龙，马洪磊，张 强，秦 宁

(西南交通大学地球科学与环境工程学院，四川成都 610031)

铁路既有线经过长期运营必然会产生变形，在纵断面上一般表现为沉降变形。由于离心力的影响，铁路竖曲线的沉降尤为严重。文献[1]指出，铁路提速后竖曲线地段轨道动态检测时常出现超限值，影响旅客乘坐舒适度。为及时获取既有线现状的线形参数并对既有线进行整正，需定期对既有线进行复测。可采用全站仪结合轨检小车对既有轨面进行三维坐标测量，依据复测数据对铁路纵断面参数进行优化。优化的首要步骤是要进行线形分段，传统方法是依据测点正矢或曲率的变化规律，人工识别出线形分段点。

人工方法进行既有线铁路线形分段灵活性较强，但在大量既有线线形外业观测数据中，由于测量误差的影响，分段精度较低。由于分段点的选择偏差对于纵断面圆曲线最小二乘法拟合结果敏感度较高[2]，较低的分段精度会影响后续工作。基于此，本文研究一种将正矢和最小二乘原理相结合的迭代算法。

1 纵断面线形及其性质

铁路纵断面一般包括直线坡段和竖曲线两种线形，二者是纵断面线形的基本要素。两纵坡线的交点称为变坡点，为保证列车经过变坡点时轨道的平顺性，当相邻两坡段坡度差大于一定限度时，需设置竖曲线连接。我国的铁路纵断面变坡点处一般设置圆曲线型竖曲线。

竖曲线按照凹凸性不同，可分为凹形、凸形两种，如图1，设变坡点相邻两纵坡的坡度分别为i1，i2，则坡度差w=i1－i2，w的正负与竖曲线的凹凸有关，w为正时称为凸形竖曲线;反之，称为凹形竖曲线。转向角α=±(arctani1－arctani2)，竖曲线半径R一般采用设计值或拟合值，由此可计算竖曲线诸要素，计算公式参见文献[3]。

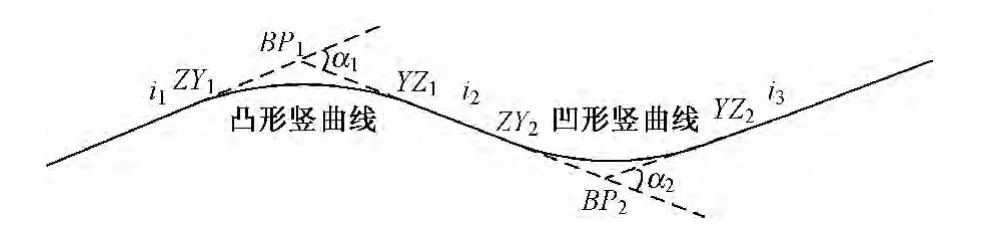
图1 道路纵断面线形示意

在铁路纵断面，分段点里程可通过变坡点里程按照公式(1)进行计算。

式中:LZY，LYZ为两分段点(直圆点ZY、圆直点YZ)里程，LBP为变坡点的里程，T为圆曲线切线长。

2 线形参数的最小二乘法拟合

线路线形测点的高程观测值是服从正态分布的随机变量，依据最小二乘原理来拟合直线坡段和圆曲线，可以使各观测点高程与拟合高程的偏差平方和达到最小。铁路纵断面上，观测的离散点可用里程和高程表示出来，进而可以依据最小二乘准则，确定线形参数。

纵断面线形参数主要包括直线坡段的斜率与截距和圆曲线的半径与圆心。根据轨道实测点坐标和优化线形可计算出测点中线里程，结合测点的高程数据，对于相应线形的测点可依据最小二乘原理来计算其线形参数。考虑到纵断面只需对高程进行平差计算，直线坡段的斜率与截距宜采用普通最小二乘法拟合，文献[4]中有详细的计算过程。圆曲线半径与圆心的最小二乘法拟合可按照下面的步骤进行。

首先由位于圆曲线两端和中部的3个点，求出圆曲线方程中的参数近似值X，Y，R0，这3点的里程和高程分别为 (X1，Y1)，(Xn/2，Yn/2)，(Xn，Yn)。设圆心坐标为(XO，YO)，半径为R，可得如下关系式:

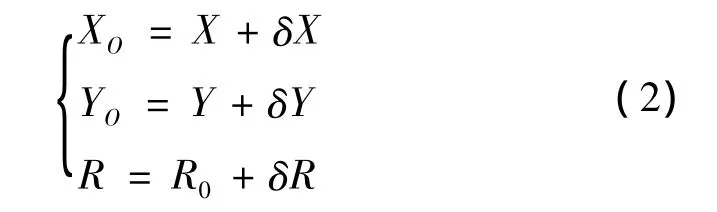
式(2)中，δX，δY，δR 为参数近似值改正数。依据最小二乘准则，若w为坡度差，则可得拟合圆曲线的误差方程

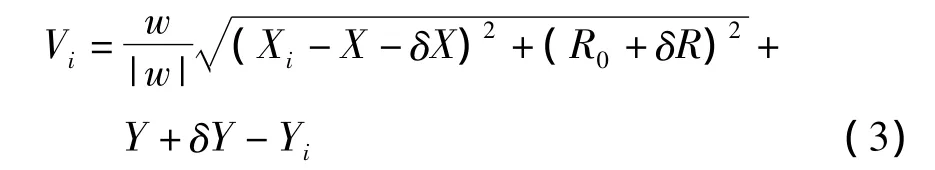
将式(3)用泰勒级数展开并线性化，通过间接平差计算即可得到拟合圆曲线圆心坐标和半径的最优解。

线形拟合完成后，可通过验后单位权中误差来对各线形的拟合效果进行分析，也可通过拟合残差平方和对线形整体拟合效果进行分析。验后单位权中误差越小，相应线形拟合效果越好。验后单位权中误差为

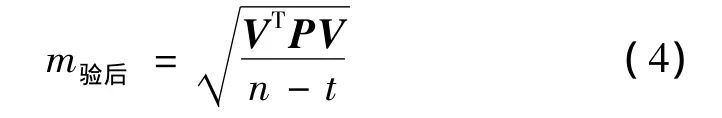
式中，V为改正数向量，P为权阵，n为拟合点个数，t为参数的个数。

3 改进的基于正矢的分段方法

3.1 计算正矢

正矢计算简图如图2所示，若以里程为横轴、高程为纵轴建立直角坐标系，任取铁路线上等间隔的3个测点，记为 j－ 1，j，j+1，则 3 点坐标为 (xj－1，yj－1)，(xj，yj)，(xj+1，yj+1)，x，y 分别表示测点的里程和高程。依据测点正矢的定义可得测点正矢fj的计算公式为

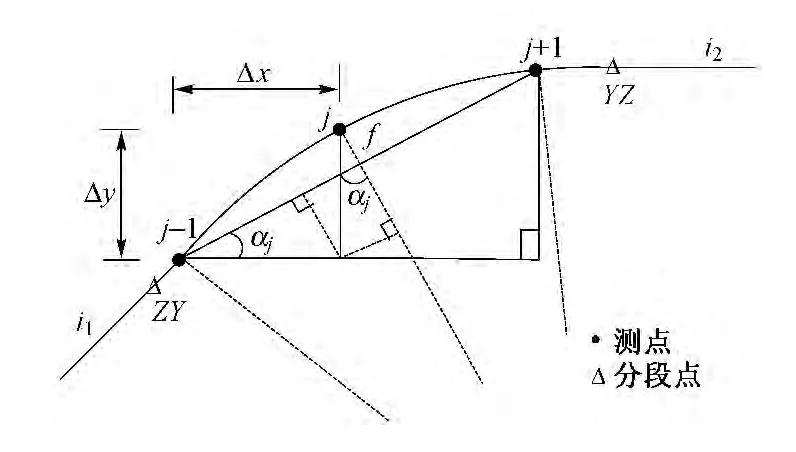
图2 正矢计算简图

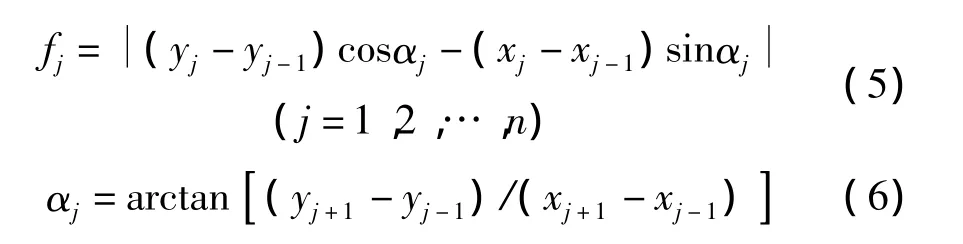
式中，αj为测点j对应弦长的倾角，也即转向角。

若不考虑测量误差和轨道变形的影响，理论上当正矢对应的弦线两端点都处于同一种线形时，线形分段较为简单，因为圆曲线上的测点在弦长一定时其正矢相等，直线坡段上的测点任何时候其正矢均为零;当计算正矢弦线的两端处于不同线形时，直线坡段和圆曲线连接处附近测点一定弦长的正矢呈线性变化，并且直圆点、圆直点位于测点时其正矢为圆曲线正矢(记为f)的1/2。纵断面线形一般为直线坡段—圆曲线—直线坡段的复合曲线，其测点正矢变化规律如图3所示。

图3 正矢变化规律

3.2 阈值与弦长的确定

实测数据由于受测量误差的影响波动较大，线形分段阈值应易于与测点高程中误差所引起的计算测点正矢误差相区分。为便于分段，线形分段阈值又分为直线坡段上测点正矢阈值fl和圆曲线上测点正矢阈值fO。由于不考虑里程误差的影响，且竖曲线转向角一般为一较小值，依据误差传播定律，测点正矢的中误差约为测点高程中误差的倍。为便于线形分段阈值与其误差进行区分，fl可取3倍的测点高程中误差;又因为圆直点、直圆点位于测点时其正矢为圆曲线正矢f的1/2，所以fO可取圆曲线正矢的一半。为与直线坡段测点进行区分，可设置fO为fl的2倍。阈值确定后，测点所属区段和阈值有如下关系:测点正矢＞fO时，测点位于圆曲线段上;测点正矢＜fl时，测点位于直线坡段上;其余测点位于分段点附近。fO确定后，进而大致确定圆曲线正矢f=2fO，再由式(7)确定弦长Lxc。

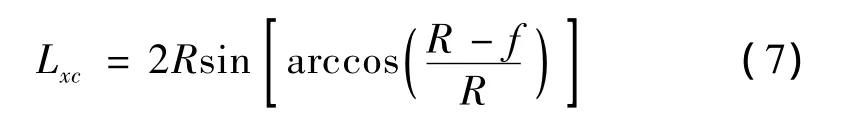
式中:R为圆曲线半径设计值，应根据设计文件或线路设备台账来确定。

计算每个测点以Lxc为弦长的正矢，进而可得测点正矢变化规律图。经试验得出:弦长适中(如图4中后两段竖曲线附近)，测点正矢呈梯形变化;弦长过大(如图4中前两段竖曲线附近)，测点正矢呈三角形变化;弦长过小时(如图5)，正矢变化杂乱无章。弦长适中或过大均可依据正矢实现分段，相比第一种情况分段效果更好，弦长过小时不能依据正矢进行分段。据此原则调整弦长，以便能够通过正矢正确分离出属于不同线形的测点。

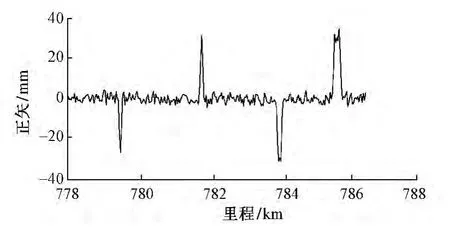
图4 易于分段的测点正矢图像

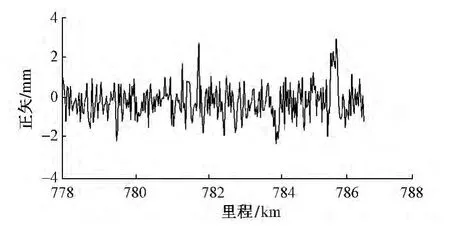
图5 不易分段的测点正矢图像

3.3 线形分段算法

铁路既有线经平面优化设计，根据轨道实测点坐标和优化线形可计算测点的中线里程，结合从外业观测数据中提取的测点高程，建立里程、高程直角坐标系，依据二者的函数关系即可进行纵断面的分段计算。算法步骤如下:

1)首先依据测量高程中误差推算阈值，再计算圆曲线正矢，由圆曲线正矢按公式(7)计算弦长，进而搜索每个测点所对应弦长两端的临近测点，按照公式(5)计算复测曲线上该测点的正矢(两端默认为直线坡段，测点正矢为0)，依据测点正矢图像通过改变弦长来对测点正矢进行调整，直到利用该弦长下的测点正矢易于实现分段为止。

2)考虑到测点中可能存在由于测量粗差而引起的测点正矢与相邻测点正矢相差较大的点，可通过比较差值是否超过了一定限值来判断该点观测值是否是粗差，并予以剔除。

3)依据测点正矢与线形的关系，分离出直线坡段上的测点，近似统计圆曲线上测点个数q，对直线坡段的测点进行最小二乘法拟合，由拟合出的线形参数计算变坡点和转向角。

4)搜索曲线上距离变坡点最近的点，易知该点一定位于圆曲线上。选出该测点大里程方向和小里程方向各p个测点，用这些测点来拟合圆曲线参数，进而计算圆曲线要素。

5)按照公式(1)计算分段点里程，依据分段点里程区分出属于直线坡段的测点和属于圆曲线的测点，再次拟合直线坡段和圆曲线，重新计算变坡点、切线长和分段点，直到分段点坐标稳定为止。

6)分段后，运用相应线形的参数对直线坡段、圆曲线测点进行重新计算，可得到拟合后的任一测点里程对应的高程，依据公式(4)计算验后单位权中误差，进而对拟合效果进行分析。由于圆曲线线形参数对参与最小二乘法拟合的测点个数比较敏感，初值p对拟合效果影响较大。可依次增加p的个数，重复步骤(4)，(5)，(6)，计算每一次拟合的残差平方和，取残差平方和最小时的分段点坐标作为最终结果。

纵断面分段计算流程如图6所示。

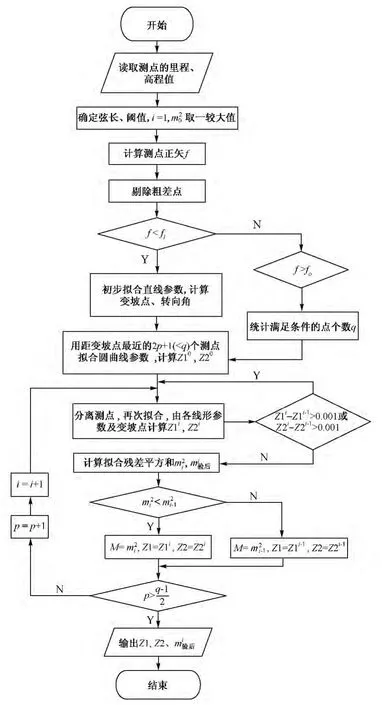
图6 纵断面分段计算流程

4 算例

按照上述算法，应用Visual C#语言编制铁路纵断面竖曲线分段拟合计算程序，以石武线的一段设计数据及其加上随机误差(±2，±3，±4 mm)后的3组仿真数据对算法进行验证，这段铁路纵断面是由5段直线坡段和4段圆曲线组成。基于以上算法，导入里程、高程数据后，输出分段点的里程和高程。表1为不同仿真误差下分段点里程设计值与计算值比较。可见，仿真误差为±2 mm时，分段误差绝对值最大为0.446 m，最小为0.033 m;仿真误差为±3 mm时，分段误差绝对值最大为0.453 m，最小为0.09 m;仿真误差为±4 mm时，分段误差绝对值最大为0.734 m，最小为0.025 m。而人工识别出的分段点误差一般在10 m左右且不易控制。表2是各线形拟合后的验后单位权中误差。可见，仿真误差为±2 mm时，验后单位权中误差最大值为1.212 mm;仿真误差为 ±3 mm时，验后单位权中误差最大值为1.81 mm;仿真误差为±4 mm时，验后单位权中误差最大值为2.352 mm。验后单位权中误差均小于仿真误差，表明各线形拟合达到了较好的效果。

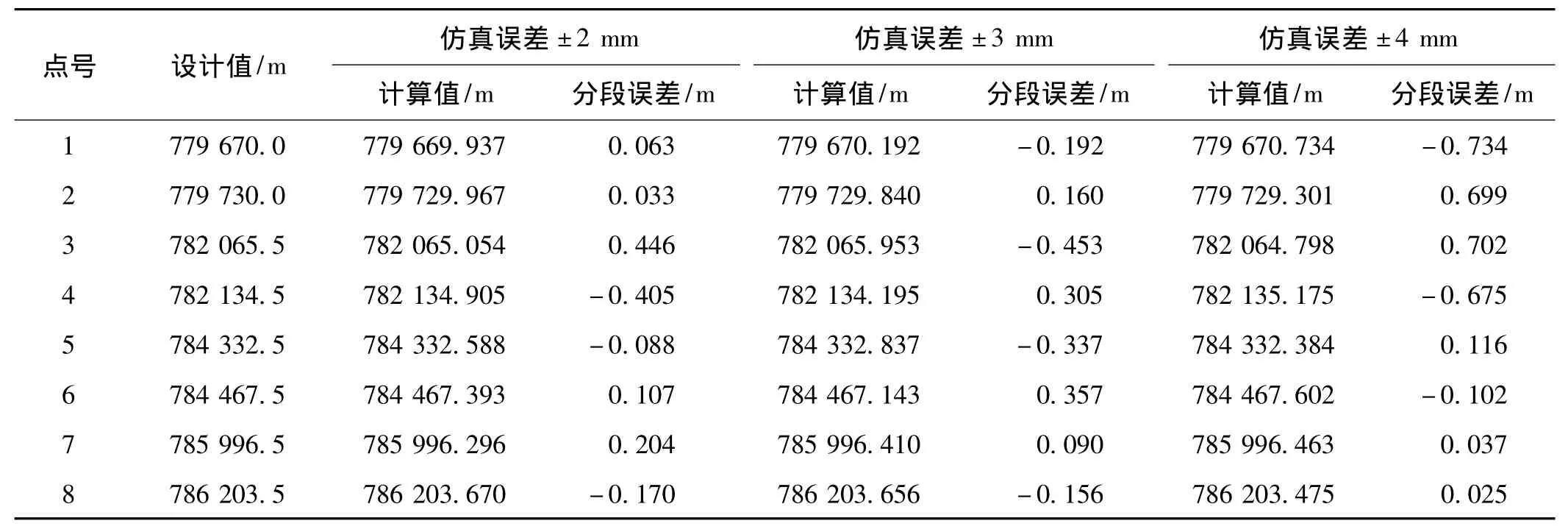
表1 不同仿真误差下分段点里程设计值与计算值的比较

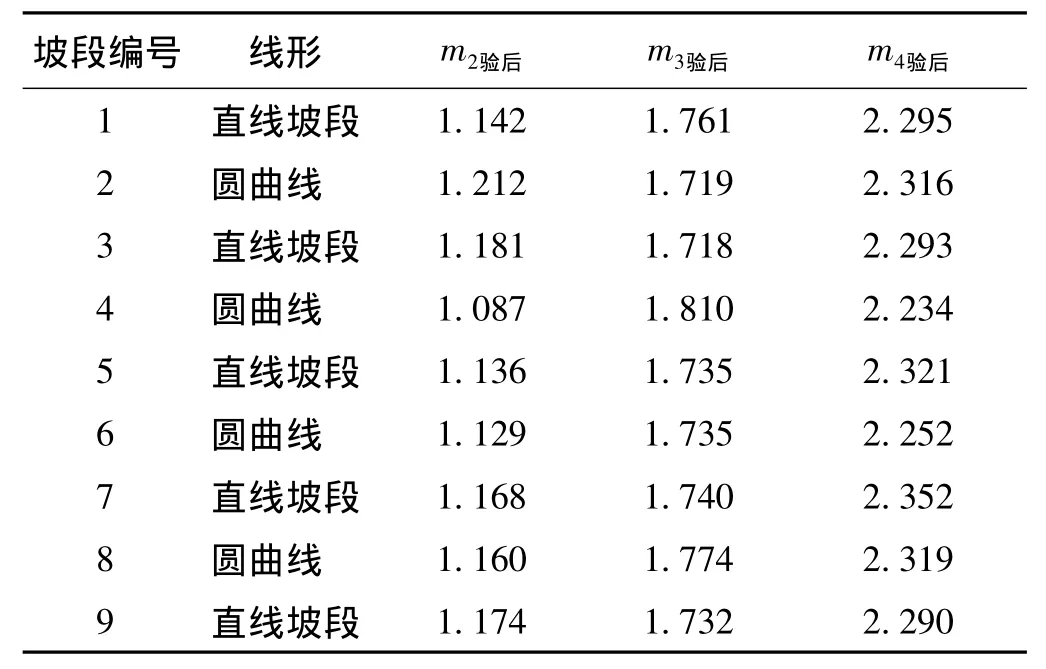
表2 各线形拟合验后单位权中误差 mm

5 结论

1)基于既有线的仿真数据，分析了纵断面线形的特点和测点正矢的变化规律，建立了依据最小二乘原理对线形参数进行拟合的模型。

2)根据所建立的计算模型，按照起落道量平方和最小的原则，实现了线形分段点的自动识别。铁路既有线纵断面线形分段采用正矢与最小二乘拟合相结合的方法，提高了分段点的精度，易于计算机编程实现。该方法克服了传统的基于曲率、正矢人工识别方法存在的分段点误差不能控制的缺点，为既有线纵断面的整正计算奠定了基础。

[1]孙贵存，胡建.铁路竖曲线整治方法的研究[C]//胶济客运专线相关技术研讨会论文集.山东:山东省科学技术协会，2009:105-108.

[2]陈锋，辜良瑶，杨岳，等.铁路既有线复测平面曲线优化方法[J].铁道科学与工程学报，2012，9(5):90-95.

[3]王兆祥.铁道工程测量[M].北京:中国铁道出版社，2000.

[4]丁克良，沈云中，欧吉坤.整体最小二乘法直线拟合[J].辽宁工程技术大学学报:自然科学版，2010，29(1):45-47.

[5]中华人民共和国铁道部.GB 50090—2006 铁路线路设计规范[S].北京:中国铁道出版社，2006.

[6]马文静.铁路轨道正矢计算新方法研究[J].铁道勘察，2012(6):1-3.

[7]丁克良，刘大杰，周全基.既有铁路曲线整正平差算法[J].测绘学报，2004，33(3):195-199.

[8]郑健，刘成龙，杨雪峰，等.轨道基准网高程测量及数据处理方法的探讨[J].铁道建筑，2011(8):121-124.

[9]李红艳，陈治亚，邢诚，等.铁路既有线曲线复测计算方法[J].中国铁道科学，2009，30(2):18-22.