圆形隧道围岩应力和位移的统一塑性解
张长安
(山东省交通规划设计院,山东济南 250031)
隧道开挖使围岩应力重分布,继而进入弹塑性变形状态。隧道处于平面应变状态,其纵向应力对其横断面内的应力和变形具有重要影响,即隧道存在中间主应力 σ2效应。目前多采用 M-C或 Hoek-Brown(H-B)强度准则对隧道进行弹塑性分析[1-3],没有考虑中间主应力σ2的影响。在岩(土)体工程中常用的还有M-N(又称广义空间滑动面 SMP)准则[4]和 D-P准则[5],这2种准则都不同程度地考虑了中间主应力σ2对材料强度的影响。本文针对M-C准则、广义M-N准则和外接圆D-P准则这3种强度准则,分析平面应变状态下其统一形式,进而建立圆形隧道围岩应力和位移的统一塑性解,研究隧道围岩分析的强度准则效应。
1 平面应变状态下3种强度准则
围岩概化为均匀、连续、各向同性的理想弹塑性材料,隧道沿纵向处于平面应变状态,其纵向应力为中间主应力。圆形隧道力学模型如图1所示。设圆形隧道内表面受支护力pi作用,无穷远处受等值地应力p0作用,图中ri和R分别为隧道半径和围岩塑性区半径。以下各准则表达式中材料强度参数均采用其抗剪强度参数,即围岩的黏聚力c和内摩擦角φ。
1.1 M-C准则
M-C准则是岩(土)体工程中应用最广泛的准则,其表达式为
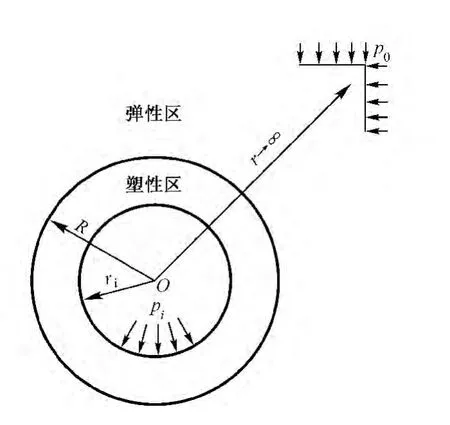
图1 圆形隧道力学模型
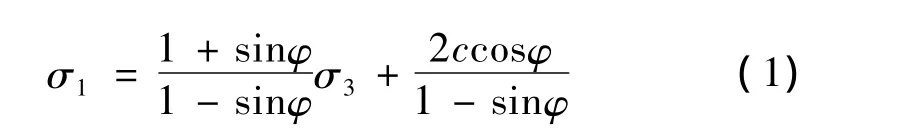
可见,M-C准则忽略了中间主应力σ2对材料强度的影响,其平面极限线为不等边六边形,如图2所示。

图2 强度准则的极限线
1.2 广义M-N(SMP)准则
广义M-N准则克服了M-C准则偏平面上的奇异性和D-P准则的拉压强度同性,并能在一定程度上反映中间主应力σ2效应,其平面极限线为曲边三角形(参见图2)。平面应变状态下广义M-N准则的表达式为[4]
式中:


1.3 外接圆D-P准则
外接圆D-P准则是广义Mises准则的一种线性形式,视中间主应力σ2与最小主应力σ3对强度的影响一样,其平面极限线为过3个广义压缩点的圆(参见图2)。平面应变状态下外接圆D-P准则的表达式为[5]

式中:
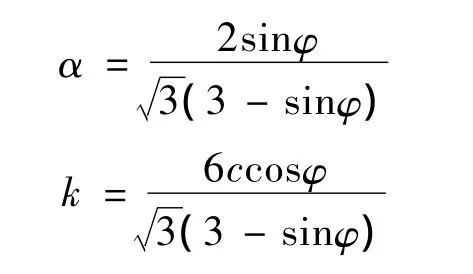
1.4 3种准则统一形式
综合比较式(1)—式(3),可以发现在平面应变状态下,这3种不同强度准则可统一写成

式中,参数M为围岩内摩擦角φ的单参数函数,参数Y为围岩黏聚力c和内摩擦角φ的双参数函数。这样就可以利用式(4)来建立圆形隧道围岩应力和位移的对应计算公式,选取不同的参数M和Y,就可以方便地得到对应不同强度准则的解。
2 围岩应力和位移
在围岩塑性区内,σ1=σθ,σ3=σr,由平衡微分方程和强度准则式(4),并以隧道内边界r=ri处σr=pi为应力边界条件,求得塑性区的应力σr,σθ分别为

围岩弹性区的应力、位移u分别为[2]

式中:E,ν分别为围岩的弹性模量、泊松比;py为围岩临界支护力。
在弹塑性交界r=R处,围岩弹性区的应力满足强度准则式(4),且r=R处的径向应力σr连续,则得围岩临界支护力py和塑性区半径R分别为

当支护力pi小于py时,围岩进入弹塑性变形状态。在围岩塑性区内,ε1= εθ,ε3= εr,假定塑性区体积应变为0,即
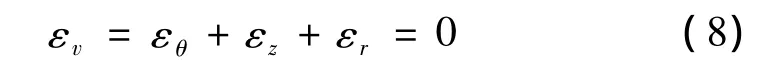
平面应变对应 εz=0,将 εr=du/dr,εθ=u/r代入式(8),并以围岩弹塑性交界r=R处的位移uR为边界条件,求得塑性区位移为

由式(6b)和式(9a)可以看出,此时塑性区和弹性区的位移表达式完全一样,只是式(6b)适用于r>R的弹性区,式(9a)适用于ri≤r<R的塑性区。
式(5)和式(9)即为圆形隧道围岩开挖时基于3种不同强度准则的应力和位移的统一塑性解。选取不同的参数M和Y,就可以得到不同的强度准则下隧道围岩应力和位移的具体计算式,应用非常方便。文献[3]的M-C准则解以及文献[4]的广义M-N准则解均是本文推导的统一塑性解的特例。
3 算例分析
主要探讨不同强度准则对隧道围岩应力和位移的影响,取隧道半径 ri=1.0 m,c=1.73 MPa,φ =25°,ν =0.3,E=1.0 GPa,初始地应力 p0=10 MPa。
不同强度准则的出发点不同,对中间主应力σ2影响的处理也不同,因而同一问题采用不同的强度准则计算,其对应结果常有差异。选取不同的参数M和Y,图3、图4分别对比了这3种准则计算的应力分布、塑性位移分布。
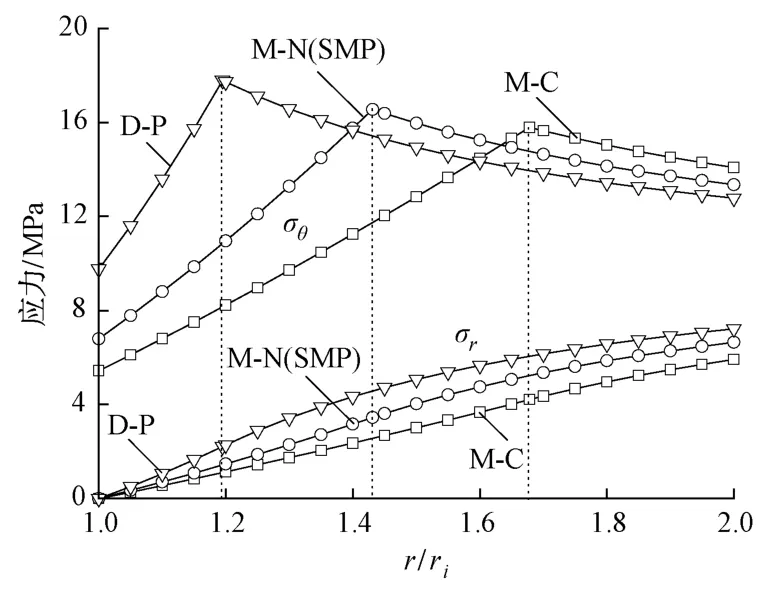
图3 应力分布

图4 塑性位移分布
由式(7)可以得出对应M-C准则、广义M-N准则和外接圆D-P准则的围岩塑性区半径R分别为1.68,1.43和1.19 m,反映在图3切向应力σθ的峰值位置以及图4塑性区位移终点的不断前移。这都说明不同强度准则对应明显不同的应力和位移分布,隧道围岩应力和位移的强度准则效应显著。同时,M-C准则对应的塑性区范围和位移最大,切向应力σθ峰值最小;外接圆D-P准则对应的塑性区范围和位移最小,切向应力σθ峰值最大;广义M-N准则的结果则处于二者之间。
上述不同强度准则计算结果间的差异实际反映的是不同准则对中间主应力σ2效应处理的差异,随着岩体中间主应力σ2效应的增加,岩体强度提高,对应的塑性区范围和位移减小,保持围岩稳定所能承受的切向应力增大。这说明不考虑中间主应力σ2影响的M-C准则过于保守,考虑中间主应力σ2可以充分发挥岩体的强度潜能和自承载能力。另外,中间主应力σ2对岩体强度的提高作用不如第三主应力σ3的作用明显。外接圆D-P准则视中间主应力σ2和第三主应力σ3的影响一样,高估了σ2的提高作用,同时也不能反映岩土材料拉压异性、应力Lode角效应等基本力学特性,因而在隧道围岩分析中应用外接圆D-P准则需谨慎,应优先选用合理考虑中间主应力σ2效应的广义M-N准则。
4 结论
1)分析可知平面应变状态下M-C准则、广义M-N准则和外接圆D-P准则具有统一的表达式,进而得到不同强度准则下圆形隧道围岩的应力和位移的统一塑性解。已有的M-C准则解以及广义M-N准则解均是本文推导的统一塑性解的特例。
2)围岩应力和位移的强度准则效应显著,本质是不同准则对中间主应力σ2效应的处理不同,考虑中间主应力σ2可以充分发挥岩体的强度潜能和自承载能力。M-C准则过于保守,外接圆D-P准则应用需谨慎,应优先选用广义M-N准则。
[1]BROWN E T,BRAY J W,LADANYI B,et al.Ground response curvesfor rock tunnels[J].JournalofGeotechnical Engineering,ASCE,1983,109(1):15-39.
[2]SHARAN S K.Analytical solutions for stresses and displacements around a circular opening in a generalized Hoek-Brown rock[J].International Journal of Rock Mechanics and Mining Sciences,2008,45(1):78-85.
[3]刘夕才,林韵梅.软岩扩容性对巷道围岩特征曲线的影响[J].煤炭学报,1996,21(6):596-601.
[4]朱建明,彭新坡,徐金海.基于SMP准则的衬砌隧道围岩抗力系数的计算[J].岩土工程学报,2011,33(5):700-704.
[5]姜福兴,刘金海,王平.基于Druker-Prager准则的煤层冲击失稳模型[J].煤炭学报,2011,36(5):727-731.

