一类含随机效应生长曲线模型的谱分解估计

崔伦建

(华北水利水电大学 数学系,河南 郑州 450000)

一类含随机效应生长曲线模型的谱分解估计

崔伦建

(华北水利水电大学 数学系,河南 郑州 450000)

对于含随机效应的生长曲线模型,当随机效应阵D和误差阵R为数乘单位矩阵时,利用向量化算法把模型转化为含两个方差分量的混合效应模型,利用谱分解法能够同时得到模型的固定效应和随机效应的谱分解估计,并给出了估计的性质.

随机效应;谱分解;方差分量

0 引言

生长曲线模型(growth curve models，GCM)是1938年WISHART在研究不同组间动植物的生长情况时引入的,该模型在计量经济、生物育种、医药研究以及流行病学等领域有着极为广泛的应用．由于研究的目的和样品取法不同,有时效应不能看成是固定的,而应该看成是随机的,即含随机效应的生长曲线模型,其定义如下，

(1)

其中Y为观察矩阵,X、A为已知设计矩阵,η为随机效应矩阵,η～(0,D,Im),E为误差阵,E～(0,R,Ip),从而Y～(XBA,XDX′+R≜∑,Ip),进一步假定η,E均服从多元正态分布,即η～Nq,n(0,D,Ip),E～Np,n(0,R,Ip),Y～Nn,p(XBA,XDX′+R≜∑,Ip).

对于含随机效应的生长曲线模型而言,∑的未知性和结构的特殊性使得回归参数估计以及协方差估计计算量大且复杂,处理过程中受到诸多因素限制.因此,需要对模型(1)作变形处理,把它化为一般的混合效应模型,通常利用向量化运算和Kroneker乘积把模型(1)转化为模型(2)，

y=Xβ+Uη+E.

(2)

对于模型(1)的研究主要集中在两个方面,一方面是有关随机效应的估计和这些估计的检验问题，另一方面是回归系数阵的估计与检验问题, 由于(1)中∑结构的特殊性和复杂性,对B的一些常见重要估计如MLE(maximum likelihood estimate)、BLUE(best linear unbiased estimate)产生了影响,文献[1]给出了B的BLUE估计.文献[2-3]研究了模型(1)在观察阵X,W,Y及D,R已知时, 回归参数阵的可B估函数KBL在非负定意义下的最佳线性无偏估计,同时给出了模型中随机效应和随机误差两种不同性质的随机变量的协方差阵D,R及其线性函数tr(CR+ΓD)的最小二乘估计,并讨论了估计的一些优良性.文献[4-5]在此基础上给出了回归参数θ的MLE,BLUE与LSE(least square estimate)相等的条件以及KBL两步估计及其无偏性.

对于模型(2),文献[6] 给出限制极大似然估计.文献[7]给出了非负的最小二乘估计.文献[8]在一元混合模型下提出了谱分解(spectral decomposition,SD)估计.文献[9]给出了一种确定互异特征根个数和协方差阵谱分解结构的简单方法.文献[10]得到非负改进的SD估计,并且较SD估计具有一致小的均方误差.文献[11]给出了含两个方差分量的多元混合效应模型方差分量矩阵的估计.文献[12]给出了多元线性混合模型方差分量矩阵的非负估计.文献[13]给出了具有异方差的线性和混合效应模型参数的谱分解估计.

1 谱分解估计基础

SD估计的基本思想是对协方差进行谱分解,对原模型进行适当变换,就可以获得若干个新的奇异模型,这些模型的协方差除了一个标量外,不含未知的方差分量.利用最小二乘统一理论,由每个模型都可以得到固定效应和特征值的一个估计,然后由这些特征值的估计便可推导出方差分量的估计.

引理1 设Ai,i=1,2,…,k为n阶实对称阵,那么当任意的Vi和Vj(i≠j)可交换,即ViVj=VjVi(i≠j)时,V1,V2,…,Vk可同时对角化.

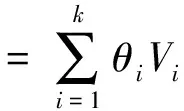
引理3 对于线性模型,可估函数c′β的一个无偏估计a′y为BLU估计,当且仅当它满足

Cov(a′y,b′y)=0,

这里b′y为零的任一无偏估计,即E(b′y)=0.

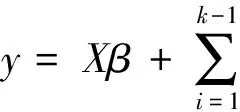
令Uk=I,ε=ηk,此时模型进一步变为如下形式，

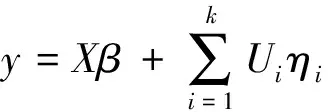
(3)

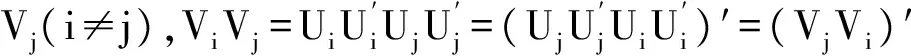
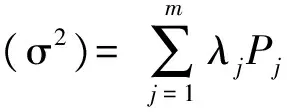
y(i)=Xiβ+ei,E(ei)=0,Cov(ei)=λiPi.

(4)

易知,Pi是奇异阵,所以该模型是奇异线性模型.注意到μ(Xi)=μ(PiX)⊂μ(Pi),由最小二乘统一理论[14]可知,模型的任一可估函数c′β的BLU估计以及λi的无偏估计分别为

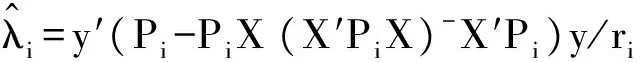
i=1,2,…,m,这里ri=tr(Pi-PiX(X′PiX)-X′Pi),称这些估计为C′β和λi的SD估计.

2 含随机效应生长曲线模型的谱分解估计

含随机效应生长曲线模型的误差阵和随机效应阵的联合矩阵∑结构的复杂性和未知性，使回归参数B估计以及协方差∑估计计算量大并且复杂,处理过程中受到诸多条件限制.因此,对含随机效应的生长曲线模型作变形处理,把它化为一般的线性混合效应模型,利用谱分解的方法同时得到其固定效应和混合效应.对于模型(1),利用向量化运算拉直运算和Kroneker乘积将其转化为如下形式，

Vec(Yn×p)=(Wp×q⊗Xn×m)Vec(Bm×q)+(Ip×p⊗Xn×m)Vec(ηm×p)+Vec(En×p)，

令H=(W⊗X),β=Vec(B),U1=Ip×p⊗Xn×m,η1=Vec(η),ε=Vec(E),此时,

y=Hβ+U1η1+ε，

(5)

其中E(ε)=0,Cov(ε)=Ip⊗R,Cov(η1)=Ip⊗(XDX′),E(η1)=0.

如果Ip⊗R=δ12Ipn,则Ip⊗(XDX′)=δ22Ipn,即模型(3)为只含有一个随机效应的生长曲线模型.令η2=ε,U2=Inp.此时把模型(1)化为一般的含两个方差分量的线性混合效应模型,即

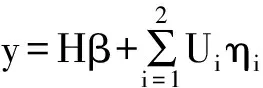
(6)

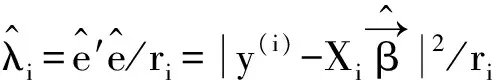
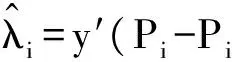
这里ri=tr(Pi-Pi(W⊗X)((W⊗X)′Pi(W⊗X))-(W⊗X)′Pi).

3 谱分解估计的性质

一般情况下，变换后所得新模型(4)的任意可估函数一定是原模型(3)的可估函数,反之不一定成立. 此外,方差分量SD估计和固定效应SD估计一般不唯一,结合线性混合效应模型有以下4个性质.

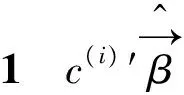
证明

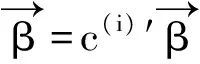
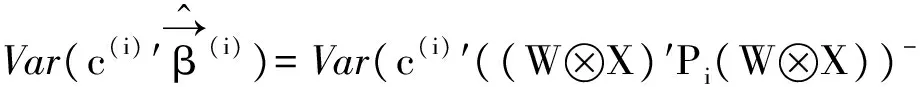
(W⊗X)′Var(Piy)(W⊗X)((W⊗X)′Pi(W⊗X))-c(i)=c(i)′((W⊗X)′Pi(W⊗X))-(W⊗X)′λiPi(W⊗X)·

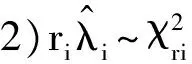
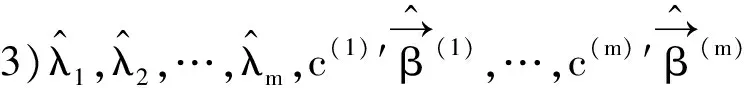
证明 结论1)参见定理1的证明,结论2)和3)参见文献[14]之定理9.22.

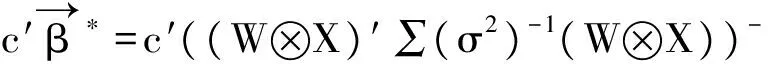
且

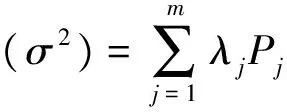
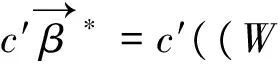
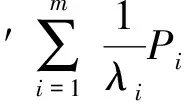
则

结论得证.

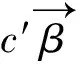
其中

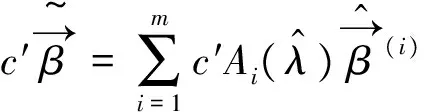
[1] 喻胜华,何灿芝.一般增长曲线模型参数阵的BLU估计[J].数学杂志,1988,18(4):439-444.

[2] 严国义,肖世永.含有随机效应的增长曲线模型回归系数阵的BLUE[J].武汉化工学院学报, 2006,28(2):79-81.

[3] 严国义.含有随机效应增长曲线模型回归系数阵与协方差阵的估计[D].武汉：华中师范大学,2011.

[4] 罗幼喜,李翰芳,李子强.含随机效应GCM中回归参数阵两步估计的计算及其无偏性[J].系统科学与数学,2008,28(12):1 545-1 554.

[5] 罗幼喜.含随机效应的增长曲线模型回归参数阵的估计[D].武汉：华中师范大学,2010.

[6] CALVIN J A, DYKSTRA R L. Maximum likelihood estimation of a set of covariance’s matrices under lower order restriction with applications to balanced multivariate variance components models[J].Ann Statist, 1991, 19(A):850-869

[7] CALVIN J A, DYKSTRA R L. Least squares estimation of covariance matrices in balanced multivariate variance components model[J].Statist Assoc,1991, 86(b):388-395.

[8] 王松桂,尹素菊.线性混合模型参数的一种新方法及应用[J].中国科学:A辑,32(5):434-443.

[9] SHI JIANHONG, WANG SONGGUI. The spectral decomposition of covariance matrices for the variance components models [J].Journal of Multivariate Analysis, 2006, 97:2 190-2 205.

[10]史建红, 王松桂.方差分量的非负估计[J].工程数学学报, 2004, 21(4):623-627.

[11]马铁丰,王松桂.含有两个方差分量的多元线性混合效应模型方差分量矩阵的估计[J].数学年刊,2009,30 (A):73-84.

[12]马铁丰,叶仁道,贾丽杰.多元线性混合模型方差分量矩阵的非负估计[J].数学学报:中文版, 2010, 53(2):349-362.

[13]李辉,崔文善,朱砾.具有异方差的线性和混合效应模型参数的谱分解估计[J].怀化学院学报,2006,25(5):5-9.

[14]吴密霞.线性混合效应模型引论[M].北京:科学出版社,2013.

The Spectral Decomposition Estimates for a Class ofGrowth Curve Models with Random Effects

CUI Lun-jian

(DepartmentofMathematics,NorthChinaUniversityofWaterResourcesandElectricPower,Zhengzhou450000,China)

For growth curve models with random effects, when the random effects matrixDand the error matrixRis a unit matrix multiple, the method of vectorization algorithm is applied to translate it into a linear mixed effects model with two variance components. Using the application of spectral decomposition to obtain the fixed effects and random effects spectral decomposition estimates at the same time, and are some natures of the estimates.

random effects; spectral decomposition; variance components

2014-05-06

崔伦建(1988—)，男，河南驻马店人，华北水利水电大学数学系在读硕士研究生.

10.3969/j.issn.1007-0834.2014.04.011

O212

A

1007-0834(2014)04-0042-05