一个带有潜伏感染和不完全治疗的肺结核模型研究

董 晶

(信阳职业技术学院 数学系，河南 信阳 464000)

一个带有潜伏感染和不完全治疗的肺结核模型研究

董 晶

(信阳职业技术学院 数学系，河南 信阳 464000)

介绍了一个带有潜伏感染和不完全治疗的肺结核传染病模型，结果表明，持续振荡不可能产生，地方病的大小趋于无病平衡点或某个地方病平衡点，得到了无病平衡态的全局渐近稳定性和地方病平衡点的局部渐近稳定性.

不完全治疗；基本再生数；基本置换率；局部渐近稳定；全局渐近稳定

0 引言

肺结核是由感染肺部的结核分支杆菌引起的一种传染性细菌疾病，在全世界持续引起发病和死亡.它通过患有活跃呼吸道疾病的人的咽喉与肺部溅出的飞沫在人与人之间传播.这些飞沫携带的结核杆菌只能在空气中短暂存活大约2 h，因此普遍认为，与患者的偶然接触极少导致感染[1].通常情况下，人体能抑制细菌增长，使其转入不活跃状态，但是它们仍然存活，可以再变活跃.刚感染肺结核的人不会感觉不舒服，没有任何症状，也不具有传染力，但是可以在将来某一时刻表现出肺结核病.肺结核病的症状是咳嗽(时常带痰或血)、胸痛、虚弱、体重减轻、发烧和夜间盗汗等.

据估计，全世界约有1/3的人口感染过结核分支杆菌，这是全球范围疾病与死亡的主要原因之一，亚洲与非洲尤甚[2].感染肺结核杆菌的每10个人中就有1人携带肺结核杆菌而患病，如果不治疗，每一个活跃肺结核患者平均每年传染10到15人.目前每年新发肺结核病人870万例，每年死于肺结核病的人数达200万例.

肺结核是可治疗的，全球肺结核控制进展可观，4 000多万人在“现代结核病控制策略”工程中被治愈(1995～2012年)，与此同时，多达1 000余万例的死亡因此被避免，87%的全球治疗成功率也早已超过了1991年定下的85%的目标.然而，肺结核杆菌能对治疗肺结核惯用的药物产生耐药性，这意味着药物不再能杀死病菌，多重抗药性肺结核治疗难度大、成本高，并且标准一线药物对其无效.广泛耐药性肺结核是由多重抗药性肺结核在对二线药物有抗药性时发展而成的，多种数据显示，全部肺结核病例的5%患有多重抗药性肺结核.

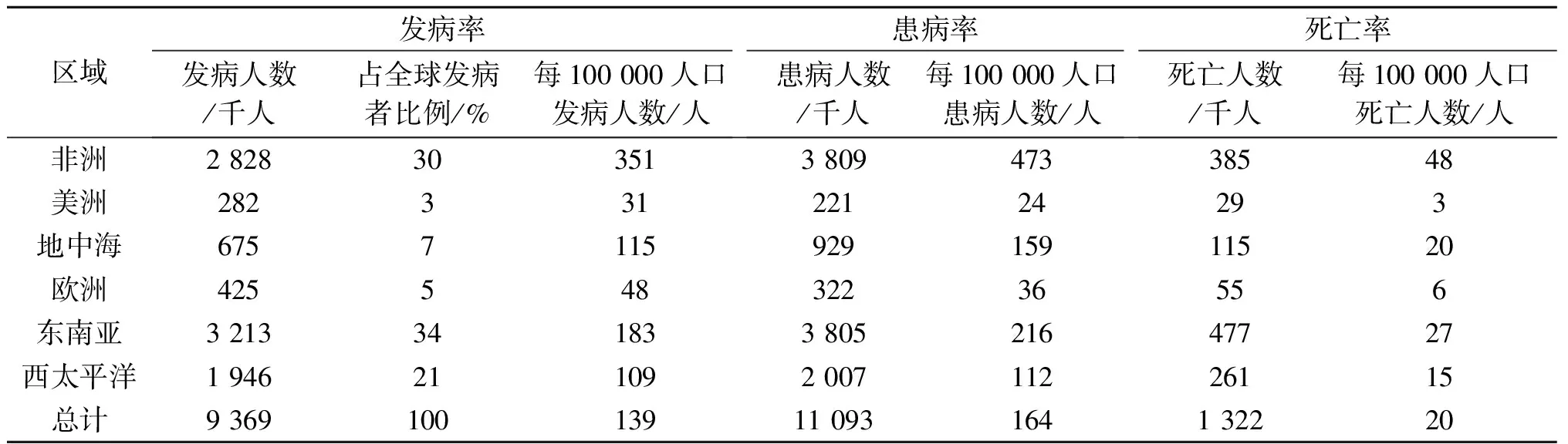
表1 2010年肺结核在不同区域的发生率、患病率和死亡率估计值

很长一段时间以来，肺结核传染病动力学受到了相当关注，不同的数学模型合并多方面因素都已经被建立，例如急慢性阶段治疗[3]、抗药病菌、再次感染、与HIV共同感染[4]、迁移、化学预防、旧病复发、外源性再感染、季节性和年龄依赖风险等.

然而上述大部分模型假设潜伏感染的个体既没有临床症状，也不能传染肺结核病，本文假设潜伏期的人也具有随疾病发展而体现出来的传染性，考虑潜伏期有较弱的感染性和不完全治疗，构建常微分方程模型.

1 模型的建立

本节从分析带有潜伏期感染性和不完全治疗的常微分方程模型开始.由于疾病发展缓慢，模型必须加入人口数量的人口统计学变化，即假定人口指数增长.记t时刻人口总大小为N(t)，分为3类：S(t)为易感者类；E(t)为疾病潜伏者类；I(t)为染病者类，可能在接受不完全治疗后再次进入潜伏者类E(t).事实上，疾病潜伏个体也可能接受治疗康复，而进入易感者类S(t)而非染病者类I(t).此外，假设潜伏个体具有相对患病者较弱的传染力,模型形式如下，

(1)

其中b为人口的出生/补充率，μ为人均自然死亡率，k为感染衰退系数，δ为潜伏的个体具有传染性的比率，a为E类中人均康复率，γ1为I类中人均康复率，γ2为人均不完全治愈率.

假设所有的参数非负，并且μ>0，总人口规模(N=S+E+I)的动力学人口方程由Nt=bN-μN给出，有N=N0exp(rt)，其中γ=b-μ.因此，γ给出人口增长率，如果γ>0，即b>μ时，人口指数增长；如果γ<0，即b<μ，人口指数减少.γ=0的情况意味着人口是固定的，这些阈值通常依据人口统计学的再生数来解释.

2 阈值

本节先考虑用地方平衡点的存在性推导阈值，也就是基本再生数，再分析各部分代表的意义.因为模型(1)是一次齐次的，考虑归一化的方程，令s=S/N，e=E/N，i=I/N，导出下列等价的非齐次系统，

(2)

其中s+e+i=1，显然系统(2)总有一个无病平衡点P0=(1，0,0).为得出地方病平衡点的存在性，定义基本再生数

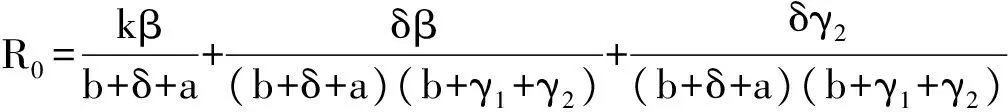
特别地，当R0>1时，有唯一地方病平衡点R*=(s*，e*，i*)，其中

(3)

及

易知R0是关于β和k的增函数，关于b，γ1和a单调递减.然而，R0与δ和γ2却有着更复杂的关系，通过计算导数得

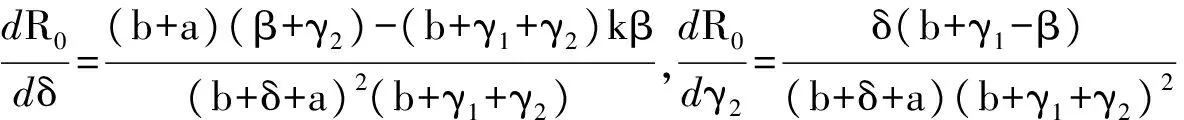
这说明当(b+a)(β+γ2)-(b+γ1+γ2)kβ>0时，R0是δ的单调递增函数；当(b+a)(β+γ2)-(b+γ1+γ2)kβ<0时，R0是δ的单调递减函数.同时，R0是γ2的单调递增函数；当b+γ1-β>0时，R0是γ2的单调递减函数；当b+γ1-β<0，由于s+e+i=1，系统(2)可以通过把s替换为1-e-i化简为等价系统(4)，

(4)

因此只需考察系统(4)的无病平衡点Q0=(0,0)和地方病平衡点Q*=(e*,i*)的性质，e*和i*已经在公式(3)中给出，分别与P0和P*对应一致.

3 无病平衡点的全局渐近稳定性

本节首先通过计算系统(4)在Q0处的雅可比行列式，证明当R0≤1时，无病平衡点是局部渐近稳定的(locally asymptotically stable, LAS)，然后选取合适的李雅普诺夫函数得到无病平衡点的全局渐近稳定性(globally asymptotically stable, GAS).

定理1 如果R0<1，无病平衡点Q0是局部渐近稳定的，如果R0=1，那么Q0是稳定的，如果R0>1，那么Q0是不稳定的.

证明 系统(4)在Q0处的雅可比矩阵为

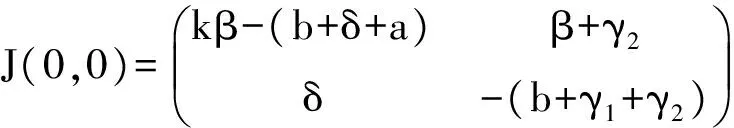
易知雅可比矩阵的两个特征值ω1和ω2满足

ω1+ω2=kβ-(b+δ+a)-(b+γ1+γ2),

ω1ω2=(b+δ+a)(b+γ1+γ2)(1-R0).

若R0<1，则ω1+ω2<0且ω1ω2>0，因此ω1和ω2均为负值，这说明Q0是局部渐近稳定的；若R0=1，其中一个特征值为0，另一个为负值，故Q0是局部稳定的；若R0>1，则矩阵存在一个正特征值，因此Q0不稳定.

定理2 如果R0≤1，则无病平衡点Q0是全局渐近稳定的.

证明 选取一个李雅普诺夫函数V=[δ+k(b+γ1+γ2)]e+(b+δ+a+kγ2)i，计算得

V′=[δ+k(b+γ1+γ2)]e′+(b+δ+a+kγ2)i′≤[δ+k(b+γ1+γ2)][λ-(b+δ+a)e+γ2i]+(b+δ+a+kγ2)[δe-(μ+γ1+γ2)i]=(b+δ+a)(b+γ1+γ2)(R0-1)(ke+i).

如果R0≤1，则V′≤0，且V′=0等价于e=i=0，故Q0全局吸引，结合定理1可以导出当R0≤1，Q0是全局渐近稳定的.

4 地方病平衡点的全局渐近稳定性

本节首先证明地方病平衡点一旦存在就是渐近稳定的.通过计算系统(4)在Q*处的雅可比行列式可得到结论，然后选取合适的杜拉克(Dulac)函数排除系统的周期解.

定理3 若R0>1，则地方病平衡点Q*局部渐近稳定.

证明 系统(4)在Q*处的雅可比矩阵为

其中l=ke*+i*，在系统(4)中令导数为0得出地方病平衡点，故雅可比矩阵第(1，1)位置的式子可以写为

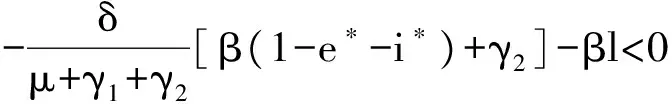
则易知两个特征值ω3和ω4满足ω3+ω4<0和ω3ω4=βl(b+γ1+γ2+δ)>0，说明两个特征值均为负值，因此断定Q*局部渐近稳定.

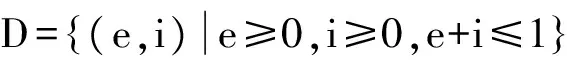
推论1 系统(4)在D内没有周期解、同宿环或者定向多边形.

由定理3和推论1，立即得到下列定理4：

定理4 若R0>1，地方病平衡点Q*全局渐近稳定.

5 基本置换率

地方病的比值可能达到地方病平衡点或者无病平衡点，无论哪种情况总人口大小的增加、减少或者不变都依赖于增长率r.类似地，比例的性质并不能充分反映出染病类总体I(t)的性质.特别地，如果感染者数量指数增长，但速度比总人口增长得慢，则二者的比值趋于0，也就是总人口的增长胜过患病者的增长，结果比值越来越小.可以想象相反的情况——染病者和总人口都趋于0，但二者的比例几乎始终是常数(并且非0).但这种情况下，只要人口存在，疾病就会在人群中存在.为了描述I(t)的性质，此时需要另外一个阈值参数.下列术语由Thieme引进，定义基本置换率

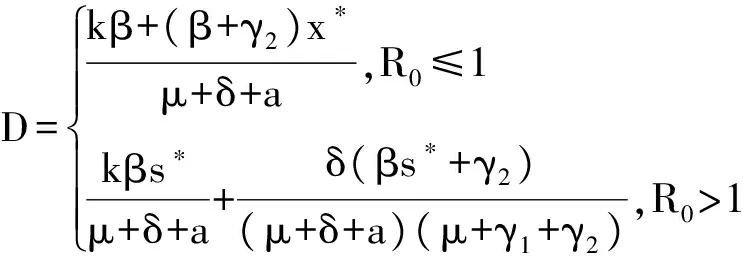
其中x*是方程的唯一正解，

(β+γ2)x*2+(kβ-δ-a+γ1+γ2)x*-δ=0.

基本置换率的有效性建立在推论2的基础上，推论2还给出了S(t),E(t),I(t)增加(减少)的指数比率.

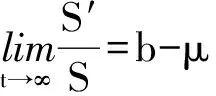
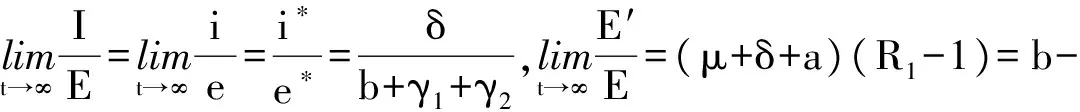
从系统(1)的第2个方程可得

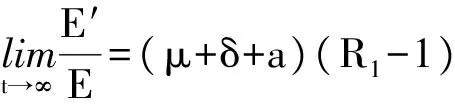
从系统(1)的第3个方程可得

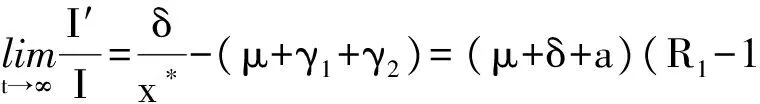
6 结论

本文建立了常见疾病肺结核的一个新模型，假设人口在潜伏阶段具有弱感染性，在潜伏阶段和染病阶段的所有人都可以接受成功或者不成功的治疗.介绍了一个简单的常微分方程模型，并证明由于地方病比例要么趋于无病平衡点，要么趋于地方病平衡点，持续振荡是不可能的.证明当R0≤1时，无病平衡点局部渐近稳定，R0>1时地方病平衡点全局渐近稳定.

[1] SONG B, Carlos C C, APARICIOJ P. Tuberculosis models with fast and slow dynamics: The role and casual contacts[J]. Math Biosci, 2002，180：187-205.

[2] DYE C, FLOYD K, UPLEKARM. World health report 2008: Global tuberculosis control: Surveillance, planning, financing[R]. World Health Organization, 2008:393.

[3] BHUNU C P, GARIRA W, MUKANDAVIRE Z. Modeling HIV/AIDS and Tuberculosis Coinfection[J]. Mathematical Biology,2009,71:1 745-1 780.

[4] LIH-LNG W R, FENG ZHILAN, CARLOS C C. Modeling TB and HIV coinfections[J]. Math Biosci Eng, 2009, 6:815-837.

A Tuberculosis Model withInfectivity in Latent Period and Imperfect Treatment

DONG Jing

(DepartmentofMathematics,XinyangVocationalandTechnicalCollege,Xinyang464000,China)

An epidemiological model of tuberculosis with infectivity in latent period and imperfect treatment are introduced. As is shown that sustained oscillations are not possible and the endemic proportions either approach the disease-free equilibrium or an endemic equilibrium. The global asymptotic stability of the infection-free state is established as well as local asymptotic stability of the endemic equilibrium.

imperfect treatment; basic reproduction number; basic replacement ratio; locally asymptotically stable; globally asymptotically stable

2014-06-10

董 晶(1983—)，男，河南信阳人，信阳职业技术学院数学系讲师.

10.3969/j.issn.1007-0834.2014.04.008

O29

A

1007-0834(2014)04-0030-05