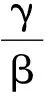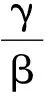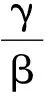差分方程在经济动态分析中的应用
欧阳瑞,王 满
(1.周口师范学院 数学与统计学院,河南 周口 466001; 2.南阳理工学院 数理学院,河南 南阳 473004)
差分方程在经济动态分析中的应用
欧阳瑞1,王 满2
(1.周口师范学院 数学与统计学院,河南 周口 466001; 2.南阳理工学院 数理学院,河南 南阳 473004)
运用差分方程的相关理论,对几个具体的经济模型进行了讨论,并结合经济动态分析的理论,展示了差分方程在经济动态分析中的应用.
经济动态分析;价格函数;蛛网模型
0 引言
经济动态分析,主要是比较相邻时期的经济发展和相近时刻的经济发展状态,并分析其发展变化的原因[1].这里所说的“相邻时期”和“相近时刻”的选择,通常依赖于经济发展变化的速度和研究经济活动手段及工具的现代化程度.比如,发达国家金融和股票市场分析是以“小时”为单位计算的,而宏观经济分析则大多是按照月份进行的.
经济动态分析关注的核心,是经济系统从一个状态转变到另一个状态时,经济变量是如何随时间变化的.这类增加了时间维度的经济模型,跟静态经济学比较而言,对于经济发展显然具有更为现实的指导意义.对于国民经济增长、国债积累、农产品供给、能源消费、人口增长等经济系统的动态分析,最终往往可以归结为一个自治方程或者自治方程组.如果以连续方式来描述时间,那么进行动态分析的结果通常是自治微分方程(组),如果以离散方式来描述时间的话,进行动态分析的结果通常是自治差分方程(组)[2].
在经济管理领域的大量实际问题中,经济数据的统计大多是按等间隔时间周期进行的,比如国内生产总值、国内人口数量等是按年统计的,而CPI、工业增加值增长速度和社会消费品零售总额等数据则是按照月份来统计的.因此,在经济动态分析中,很多经济变量的取值都是呈离散状态的[3].将时间视为离散变量进行经济动态分析的一个行之有效的工具便是差分方程及其相关理论[4].本文利用差分方程的有关理论,通过几个典型的经济问题模型,对差分方程在经济动态分析中的应用进行探讨.
1 差分方程在市场经济供求关系价格函数中的应用
1.1 供求关系中价格函数的微分方程
假设有一种商品,它的价格P是关于时间t的函数P=P(t),供给量和需求量都是价格P的函数,其中供给量S是由供给函数S=f(P)决定的,而需求量是D,由需求函数D=g(P)决定.经济学上可以假定f(P)是P的增函数,g(P)是P的减函数,且

(1)
其中a,b,c,d都是正的常数,也就是说,供给量S和需求量D都是关于价格P的函数,并且是线性的.假定S=D,则可以解得
(2)
这里的P称为均衡价格[5].显然,当S>D(即供给大于需求)时,价格将是负增长趋势,而当S (3) 其中α是正的比例系数.将(1)式代入(3)式得 (4) 其中k=α(b+d),h=α(a+c). 式(3)说明价格P是关于t的一阶常系数非齐次线性微分方程,容易求得其通解为 (5) 而满足初始条件P(0)=P0的特解为 (6) 1.2 价格函数差分方程 用差分运算代替微分运算,即 (7) 为方便起见,可以取Δt=1,则式(4)可以近似化为离散型一阶常系数差分方程, P(t+1)+(k-1)P(t)=h, (8) 利用一阶常系数差分方程的求解方法,可以求得该方程的通解为 (9) 其中c为任意常数. 满足初始条件P(0)=P0的特解为 (10) 1.3 解的稳定性及经济意义 差分方程建模的意义,不仅在于方便地对离散时间系统进行求解和计算,更在于能深入研究均衡点的稳定性条件. 1-k<1或者0 (11) 将k=α(b+d)代入式(11),可得 (12) 式(12)的经济学意义为:b是供给函数的斜率,表示价格P上涨一个单位时商品供应量将增加b个单位;d是需求函数的斜率的绝对值,表示价格上涨一个单位时商品需求量将减少d个单位.由式(12)可以看出,当供给函数f(P)固定时,即b固定时,d越小越有利于经济的稳定;当需求函数g(P)固定,即d固定时,b越小越有利于经济的稳定;而当b,d都很大时,将会导致经济发展出现不稳定因素[6]. 蛛网理论诞生于1930年,是由美国人舒尔茨等提出来的.它是一种动态分析的方法,因为价格与产量连续波动的图形与蛛网非常相似,因此命名为蛛网模型[7]. 2.1 模型的建立 蛛网模型可以用下面3个方程表示, (13) (14) (15) 其中α,β,δ,γ>0,方程(13)称为需求函数,方程(14)称为供给函数,方程(15)是均衡条件.将(13),(14)代入(15)式可得一阶线性差分方程 α-βPt=-δ+γPt-1, (16) 由(16)可得 (17) 假设市场均衡,均衡价格Pe=Pt=Pt-1,由(16)式可得均衡价格为 (18) 将(18)式代入(17)式,可得 (19) 2.2 模型分析 分析(19)式,可得以下3种情况: [1] 王潼.国民经济动态分析方法[J].数量经济技术经济研究,1988(6):9-14. [2] 董庆华.动态经济分析中自治方程的均衡解与收敛性[J].北京服装学院学报,2012,32(2):69-74. [3] 杨清霞.浅谈差分方程的应用[J].中央民族大学学报:自然科学版,2006,15(3):282-285. [4] 刘德龙.浅谈差分方程常数线性系统在动态经济分析中的应用[J].经济研究导刊,2011(31):5-12. [5] 陈放.均衡价格——动态市场价格的形成与变化趋势[J].财经问题研究,2002,222(5):11-13. [6] 李苏桓,杨凌.基于政府预算方程的希腊债务危机成因实证分析[J].财会金融,2013(5):45-47. [7] 吴光宇.基于数学模型的蛛网理论解析[J].内蒙古农业大学学报,2012,33(2):223-225. Application of Difference Equations in Economic Dynamic Analysis OUYANG Rui1, WANG Man2 (1.SchoolofMathematicsandStatistics,ZhoukouNormalUniversity,Zhoukou466001,China;2.SchoolofMathematicsandPhysics,NanyangInstituteofTechnology,Nanyang473004,China) Using the theory of difference equations, several specific economic models are simply discussed, and combined with the theory of economic dynamic analysis, the application of difference equations in the economic dynamic analysis is presented. economic dynamic analysis; price function; cobweb model 2014-07-30 河南省软科学研究计划项目(13240041102) 欧阳瑞(1979—),男,河南许昌人,周口师范学院数学与统计学院讲师. 10.3969/j.issn.1007-0834.2014.04.007 F22 A 1007-0834(2014)04-0027-03


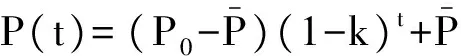
2 差分方程在蛛网模型中的应用