基于自适应超高斯混合模型的语音增强算法
赵改华 周 彬 张雄伟
(解放军理工大学指挥信息系统学院,南京,210007)
引 言
在语音通信过程中,语音信号不可避免地会受到噪声的干扰,影响通信质量和语音信号的后续处理,语音增强技术是从带噪语音中尽可能提取原始纯净语音的重要手段,在提高语音可懂度、改善语音通信质量等方面有重要的应用。在众多的增强技术中基于统计模型的短时谱估计法以其复杂度低和相对有效的特点,长期以来受到了广大研究者的广泛关注。
基于统计模型的短时谱估计语音增强算法,主要是在不同的语音和噪声先验分布模型假设条件下,依据一定的准则,如:最小均方误差(Minimum mean square error,MMSE)、最大后验概率(Maximum a prosteriori,MAP)、最大似然值(Maximum likelihood,ML),对语音信号的短时谱进行最优估计。经典的基于统计模型的短时谱估计法是由Ephraim和Malah提出的基于高斯模型的最小均方误差短时幅度谱(Short-time spectral amplitude-minimum mean square error,STSAMMSE)[1]估计算法。对语音信号统计模型的深入研究表明,超高斯模型更符合语音信号的实际分布[2],据此,研究者提出了许多改进算法,例如文献[3~6]提出的基于超高斯语音模型的短时谱估计算法,包括基于超高斯模型的复频谱MMSE估计算法、基于超高斯模型的幅度谱MAP估计算法、基于Gamma模型的DCT域MMSE估计算法和基于超高斯模型的对数谱MMSE估计算法,相对于基于高斯模型的增强算法增强效果有所提升。
上述增强算法都假设语音信号幅度谱服从单一的分布函数,而事实上,由于语音信号产生的复杂性及其非平稳性,其分布很难用单一的函数准确描述[7]。因此,研究者提出了一些利用较为复杂的混合模型为语音信号建模的新方法,如文献[8]提出的基于高斯混合模型复频谱MMSE估计算法,文献[9]提出的基于瑞利混合模型的幅度谱MMSE估计算法,近年来,研究者提出了一些高斯混合模型的改进模型来进一步提高增强效果,例如:文献[10]提出的基于高斯尺度混合模型的对数谱估计算法,文献[11]提出的基于超高斯混合模型的幅度谱MMSE估计算法。相对于采用单一模型的增强算法,增强效果有较大提高。然而,这些混合模型对每帧语音信号建模时所用的混合分量及其权重都是固定的,而事实上,语音信号幅度谱的实际分布是动态变化的,每个混合分量与当前语音信号的相似度也是变化的,因此,固定的权重并不合理。同时,有些混合分量与当前语音信号相差较大的,将其引入混合模型不利于逼近当前语音信号的实际分布[12]。
针对上述算法存在的问题,本文提出了一种基于超高斯混合模型的语音增强算法。首先,采用EM算法将语音信号分为多个分量;然后,在增强过程中选择与当前帧相似度较大的部分混合分量,并利用初始增强语音更新选中混合分量的概率密度函数(Probability density function,PDF);其次,估计对应每个选中混合分量的幅度谱最小均方误差估计式,并依据混合分量与当前帧的相似度更新对应的子类增强语音的权重;最终的增强语音由子类增强语音的加权和获得。
1 传统短时谱估计算法
假设s(n)表示纯净语音信号,x(n)表示加性噪声信号,那么时域带噪语音信号可表示为y(n)=s(n)+x(n),对时域带噪语音信号进行分帧、加窗和STFT变换,得到带噪语音信号在频域内的表示为
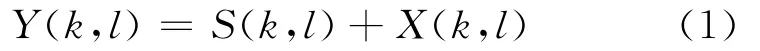
式中:l(l=0,1,2,…)表示帧序号;k(k=0,1,…)表示频带序号,用幅度和相位表示为

一般地,假设噪声复频域系数的实部和虚部分别服从高斯分布,则噪声幅度谱系数服从瑞利分布[8],表示为
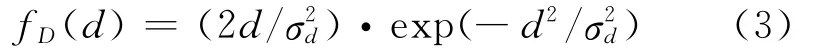
式中表示噪声系数方差。假设语音复频域系数的实部和虚部也分别服从高斯分布,则语音幅度谱系数服从瑞利分布,表示为

式中表示语音系数方差,纯净语音的MMSE估计式为[1]
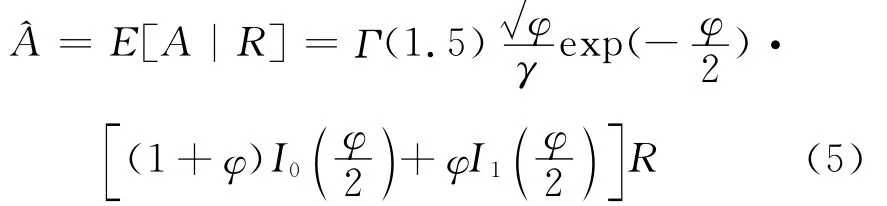
2 本文算法
如前文所述,语音信号的复杂性和非稳定性决定了用单一的函数描述语音信号幅度谱的分布是不准确的,据此,本文提出了基于自适应超高斯混合模型的语音增强算法,不仅可以更好地逼近当前语音信号的实际分布,而且可以跟踪语音信号幅度谱分布随帧移的动态变化。算法可分为3个模块:训练模块、预处理模块、增强模块,如图1所示。


图1 算法流程图Fig.1 Flowchart of the proposed algorithm
2.1 训练模块
训练模块作用是采用超高斯混合模型,将语音信号分为多个分量,并确定每个分量的初始PDF及权重。每个分量采用文献[4]推导的语音信号幅度谱的超高斯分布建模为
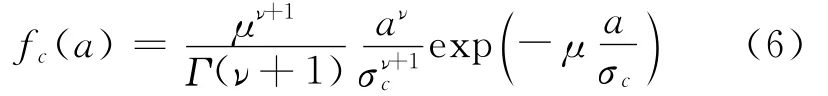
通过不同的参数(μ,ν)取值,式(6)可以非常精确地逼近对应的Gamma和Laplace分布。大量实验数据表明语音信号幅度谱的实际分布介于Gamma分布和Laplace分布之间,本文采用能够较为准确地逼近语音信号幅度谱实际分布的参数组:(μ=1.74,ν=0.126)[4]。语音信号幅度谱的超高斯混合分布表示为C个子分量的加权和,表示为

式中ωc表示每个分量的权重,且满足限制条件

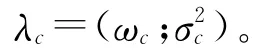
2.2 增强模块
增强模块是整个算法的核心部分。首先,选择与初始增强语音似然值最大的I个分量并更新其PDF;然后,利用更新之后的PDF计算对应选中分量的最小均方误差估计式,并利用初始增强语音与对应分量的似然值计算子类增强语音的权重;子类增强语音加权求和即得到最终的增强语音。
2.2.1 子类的选择及更新
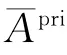
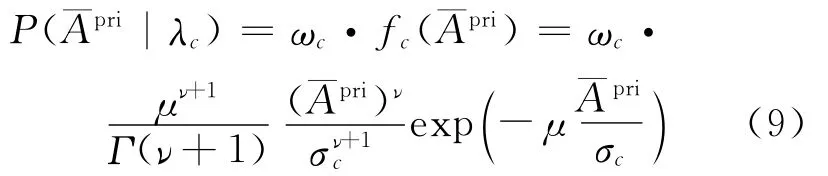

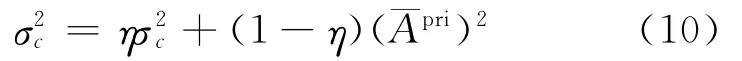
式中η表示模型更新的速度,在试验中观察到η=0.95较为合适。
2.2.2 子类增强语音及其权重的估计
假设噪声服从高斯分布,则语音信号的幅度谱的MMSE估计式表示为[1]

式(11)中零阶贝塞尔函数可以近似表示为[13]
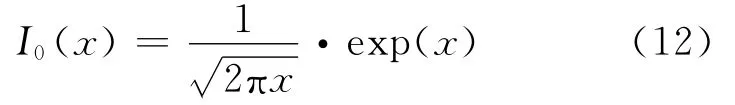
假设语音信号的幅度谱服从超高斯分布,将近似式(12,6)代入式(11),根据文献[13]中的公式3.462.1,求积分获得I类增强语音的幅度谱MMSE估计式为
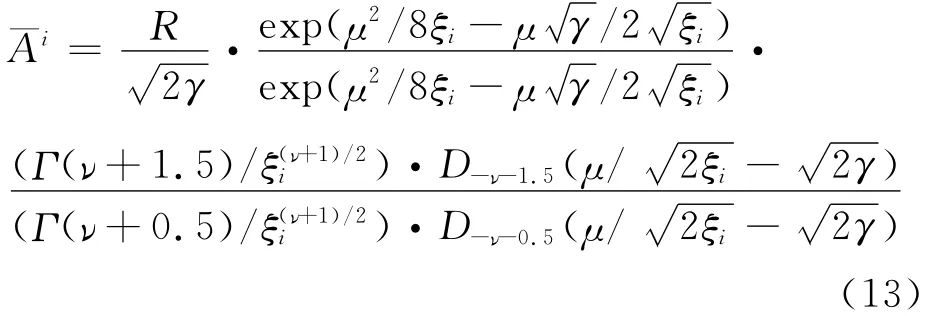
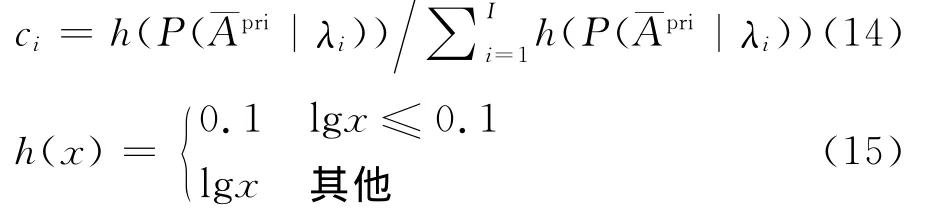

3 实验仿真
仿真实验在MATLAB环境下进行,将本文提出的增强算法与以下2种算法进行比较,包括:文献[6]提出的基于超高斯模型的MMSE对数谱估计法;文献[9]提出的基于瑞利混合模型的MMSE幅度谱估计法。为简化表示,这两种算法分别表示为Super-gauss,RMM。本文提出的算法表示为:SGMM。
采用标准语音库timit中的纯净语音对超高斯混合模型进行训练。原始噪声信号从标准噪声库Noisex92中选取,包括高斯白噪声、汽车噪声,并下采样为8kHz。纯净语音信号为标准语音库timit中的标准汉语语音信号,采用8kHz采样,时间长度约为8s,男女声各8句。利用MATLAB对噪声信号和纯净语音进行混和,信噪比分别定为0,5,10dB。噪声估计采用统计最小量跟踪算法[14],先验信噪比计算采用面向判决的方法[1]为

式中α=0.98,采用增强后和增强前语音分段信噪比提高量来衡量不同短时谱估计算法的噪声抑制性能,分段信噪比定义为

表1给出了在不同噪声和信噪比条件下3种算法的分段信噪比的提高量。从表中可以看出,相较于单一成分的Super-gauss短时谱估计算法,由于采用了多种成分加权叠加的方式来更为精确地逼近语音信号的实际分布,RMM算法和本文提出的SGMM算法在抑制噪声方面有更为显著的效果。

表1 3种算法的分段信噪比提高量 dBTable 1 Improved segmental SNR of three algorithms
采用对数频谱距离LSD衡量增强语音的失真度,对数谱距离定义为
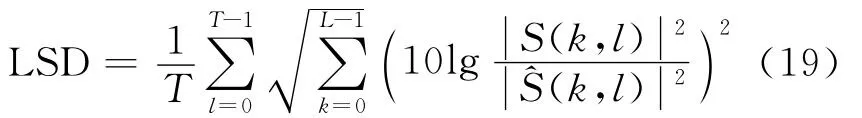
图2给出了在不同噪声和信噪比条件下的LSD改进曲线。LSD是一种语音信号失真测度,测度值越小表明语音信号谱失真越小,语音质量越接近原始语音。从图中可以看出,相较于固定模型的Super-gauss和RMM两种谱估计算法,本文提出的基于自适应超高斯混合模型的谱估计算法能够更好地描述原始语音的分布,增强语音的失真度更小。
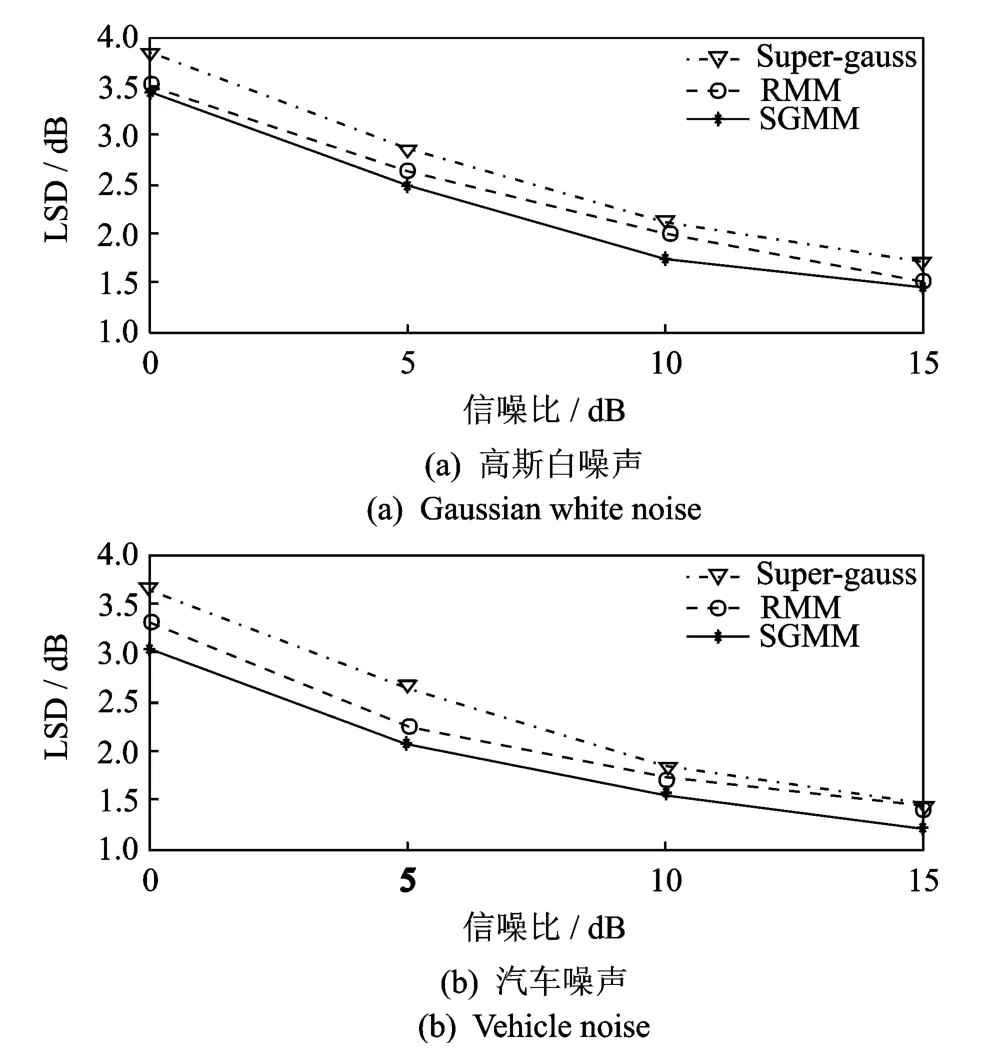
图2 对数频谱距离改进曲线Fig.2 Improved LSD curve
采用客观质量评估方法PESQ衡量增强语音的质量。表2给出了在不同噪声和信噪比条件下的PESQ评估结果,从表2中可以看出,本文算法的增强语音的PESQ得分都明显高于其他两种谱估计算法,说明其具有更好的感知质量,主观测试也验证了这一结论。
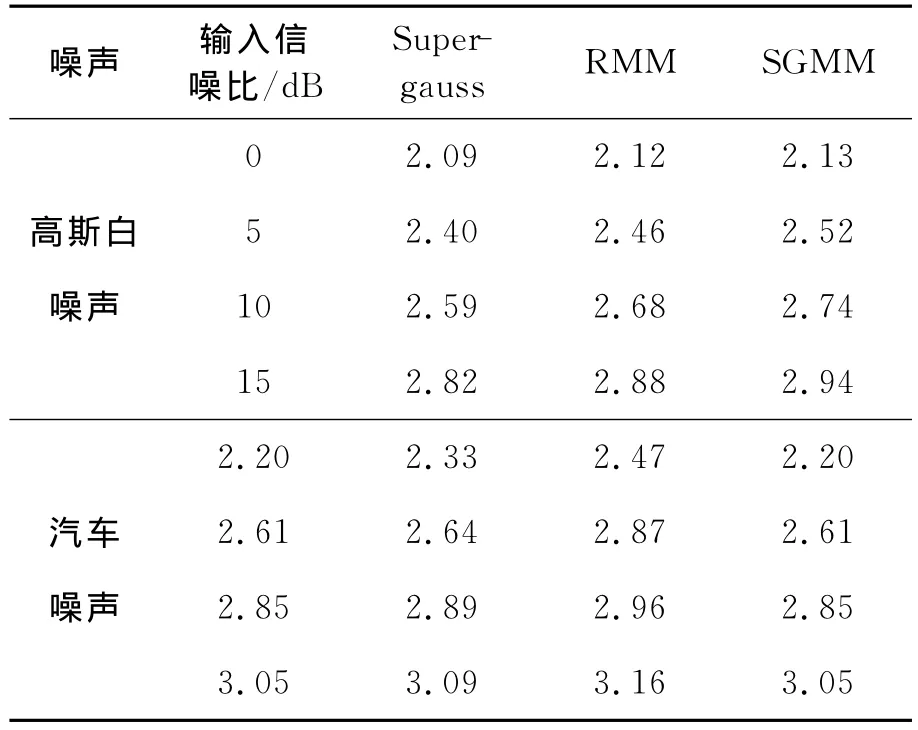
表2 四种算法PESQ评估得分Table 2 PESQ scores of four algorithms
由于在增强阶段,对于每帧语音信号都要重新选择混合分量并更新其权重,因此增强效果的提升是以计算量的增加为代价的。这也是许多类似自适应增强算法共同存在的情况[15]。
4 结束语
本文提出了一种新的基于自适应超高斯混合模型的语音增强算法,不仅将混合模型应用于超高斯幅度谱分布,且自适应更新模型参数,相对于传统的信号模型,本文提出的自适应超高斯混合模型能够更好地逼近语音信号的实际分布。仿真结果也验证了本文提出算法的优越性,不仅提高了噪声抑制性能,而且增强语音的失真度也有所下降。在下一步的工作中将针对噪声信号的非平稳性对噪声模型进行优化,有望提高算法的增强效果。
[1] Ephraim Y,Malah D.Speech enhancement using a minimum mean-square error short-time spectral amplitude estimator[J].IEEE Trans Acoust Speech,Signal Process,1984,32(6):1109-1121.
[2] Gazor S,Zhang W.Speech probability distribution[J].IEEE Signal Process Lett,2003,10(7):2042-207.
[3] Martin R.Speech enhancement based on minimum mean-square error estimation and super Gaussian priors[J].IEEE Trans Speech Audio Process,2005,13(5):845-856.
[4] Lotter T,Vary P.Speech enhancement by MAP spectral amplitude estimation using a super-Gaussian speech model[J].Eurasip J Signal Process,2005,(7):1110-1126.
[5] 邹霞,陈亮,张雄伟.一种基于Gamma语音模型的语音增强算法[J].通信学报,2006,27(10):118-123.
Zou Xia,Cheng Liang,Zhang Xiongwei.Speech enhancement with Gamma speech modeling[J].Journal on Communications,2006,27(10):118-123.
[6] Hendriks R C.Heusdens R,Jensen J.Log-spectral magnitude MMSE estimators under super-gaussian densities[J].Inter Speech,2009,10(6):1319-1322.
[7] Ephraim Y.A Bayesian estimation approach for speech enhancement using hidden Markov models[J].IEEE Trans Acoust Speech,Signal Process,1992,40(4):725-735.
[8] Ding Guohong,Wang Xia,Cao Yang,et al.Speech enhancement based on speech spectral complex Gaussian mixture model[C]//IEEE Int Conf Acoustic,Speech,Signal Process(ICASSP).Philadephia,USA:IEEE,2005:165-168.
[9] Erkelens J S,Jensen J,Heusdens R.Speech enhancement based on Rayleigh mixture modeling of speech spectral amplitude distributions[C]//European Signal Proc Conf(EUSIPCO).Poznan,Poland:[s.n.],2007:65-69.
[10]Hao Jiucang,Lee Te-Won.Speech enhancement using Gaussian scale mixture models[J].IEEE Trans on ASLP,2010,18(6):1127-1136.
[11]Wang Haiyan,Zhao Xiaohui,Gu Haijun.Speech enhancement using super gauss mixture model of speech spectral amplitude[J].The Journal of China University of Posts and Telecommunications,2011,18(1):13-18.
[12]Jancovic P,Zou X,Köküer M.Speech enhancement based on sparse code shrinkage employing multiple speech models[J].Speech Communication,2012,54:108-118.
[13]Gradshteyn I S,Ryzhik Z M.Table of integrals,series,and products[M].New York:Academic,1980.
[14]Martin R.Noise power spectral density estimation based on optimal smoothing and minimum statistics[J].IEEE Transactions on Speech and Audio Processing,2001,9(5):504:512.
[15]曹斌芳,李建奇.基于自适应仿生小波变换的语音增强方法[J].数据采集与处理,2010,25(6):741-745.
Cao Binfang,Li Jianqi.Speech enhancement method based on adaptive bionic wavelet transform[J].Journal of Data Acquisition and Processing,2010,25(6):741-745.

