四种典型波束形成声源识别清晰化方法

杨 洋 褚志刚

（1.重庆工业职业技术学院汽车工程学院，重庆，401120；2.重庆大学机械工程学院，重庆，400044）

引 言

基于传声器阵列测量的波束形成声源识别技术由于测量速度快、计算效率高等优点被广泛应用［1-8］。然而，传统波束形成（Conventional beamforming，CB）方法的输出结果是声源分布与阵列点传播函数的卷积，阵列传声器采样的有限性和离散性使其点传播函数无法等于理想的δ函数，不仅在真实声源位置输出具有一定宽度的“主瓣”，还在非声源位置输出“旁瓣”。主瓣的宽度影响声源识别的分辨率，旁瓣的出现污染声源成像图，使声源识别结果的分析具有不确定性［9］。

有效缩减主瓣宽度、衰减旁瓣干扰，清晰化声源识别结果，是提高声源识别准确度的关键，近年来备受国内外学者关注。目前，已有的波束形成声源识别结果清晰化方法主要有反卷积声源成像（Deconvolution approach for the mapping of acoustic sources，DAMAS）、反卷积声源成像扩展（DAMAS2）、非 负 最 小 二 乘 （Non-negative least squares，NNLS）、基于快速傅里叶变换的非负最小二乘（FFT-NNLS）、清除法（Clean）、基于同一声源产生的主瓣与旁瓣相干的清除法（Clean based spatial source coherence，CLEAN-SC） 等。DAMAS的基本思想是在传统波束形成输出结果、阵列点传播函数、声源分布之间建立线性方程组，通过在反复迭代过程中引入正约束来定解该方程组，从而提取真实声源信息，有效消除旁瓣干扰和主瓣宽度的影响，其最初由美国NASA的研究者［10］在2004年给出，DAMAS建立了反卷积声源成像的理论基础，但其变量多、计算量大、耗时长。DAMAS2是DAMAS的扩展方法，其假设阵列点传播函数只取决于观测点与声源点间的相对位置，而与具体位置无关，具有空间转移不变性，利用傅里叶变换将声源分布与阵列点传播函数间的卷积转化为波数域的乘积，基于FFT提高求解速度，由美国OptiNav的研究者［11］在2005年给出，相比于DAMAS，DAMAS2提高了计算效率，但计算精度有所下降。与DAMAS不同，NNLS的基本思想是在传统波束形成输出结果、阵列点传播函数、声源分布之间建立差函数，最小化该差函数来提取真实声源信息，2007年，德国DLR的研究人员［12］基于梯度投影算法求解NNLS波束形成问题，为提高求解速度，其进一步效仿DAMAS2方法，假设空间转移不变阵列点传播函数和镜像空间转移不变阵列点传播函数，从而将空间域卷积转化为波数域乘积，给出FFT-NNLS方法。CLEAN的基本思想是通过反复在传统波束形成结果中移除与主瓣峰值对应的阵列点传播函数来清晰化声源识别结果，其简单方便，计算效率高，由荷兰格罗宁根大学的Schwarz［13］在1978年引入。上述方法均需要基于单极子点声源假设计算理论的阵列点传播函数，与这些方法不同，CLEAN-SC基于同一声源产生的主瓣与旁瓣完全相干的原理，通过反复在传统波束形成结果中移除与主瓣相干的旁瓣来清晰化声源识别结果，不需要重构阵列点传播函数，从而有效避免了点声源假设的影响，计算精度较高，其最初由荷兰NLR的P.Sijtsma［14］在2007年给出。不同的清晰化思想决定了这些方法具有不同的成像规律和性能，不同方法的对比分析对其在实际工程中的准确应用具有重要指导意义。

本文阐明 DAMAS，DAMAS2，NNLS，FFTNNLS，CLEAN，CLEAN-SC清晰化方法的基本原理，基于模拟计算的声源平面上已知声源的识别成像图及计算标准差、计算时间随迭代次数的变化曲线对比分析各方法的成像规律和性能。进一步，进行基于不同方法识别人为设计的扬声器声源的算例试验，对比分析各方法在识别实际声源时的差异性。对这些方法在实际工程中的准确应用具有重要指导意义。

1 基本原理

1.1 传统波束形成

波束形成声源识别技术利用传声器阵列接收声信号，离散声源计算平面形成聚焦网格点，基于特定算法反向聚焦各网格点，使真实声源所在聚焦点的输出量被加强，其他聚焦点的输出量被衰减，从而有效识别声源［1-7］。图1（a）为波束形成声源识别布局示意图，黑色“·”表示阵列传声器，rm（m＝1，2，…，M）为m号传声器坐标向量，M为传声器数目，图示为直径0.65m的36通道COMBO阵列，“★”表示声源计算平面聚焦点，r为其坐标向量。传统波束形成的输出量

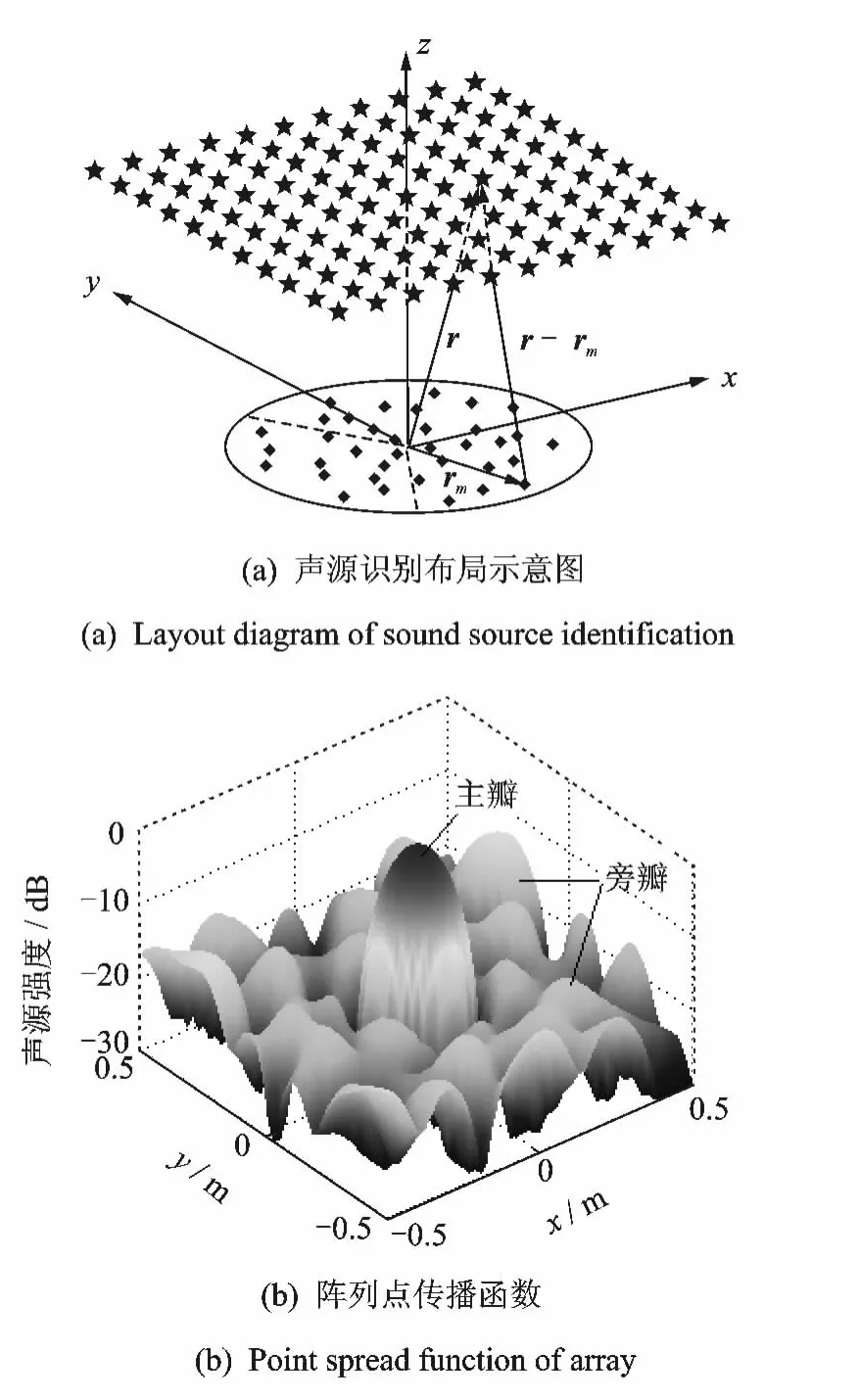
图1 波束形成原理示意图Fig.1 Principle of beamforming

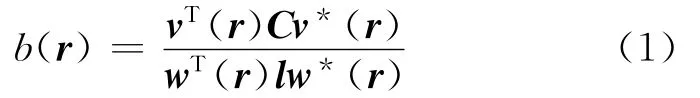
式中：C为阵列传声器接收声信号的全互谱矩阵；l为元素均为1的单位矩阵；上标T和＊分别表示向量的转置和共轭；v＝［vm（r）］为r聚焦点位置的转向列向量；w≡［|vm|2］。

转向向量的元素表达式为

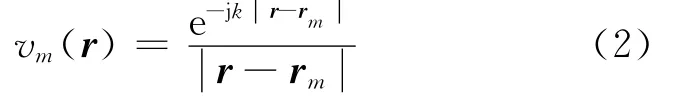
式中：k＝2πf/c为波数，f为信号频率，c为声速。

假设各声源互不相干，则阵列传声器接收声信号的互谱等于各声源分别在阵列传声器处产生声信号互谱的和，如式（3）所示，其中，r′为声源坐标向量，q（r′）为r′处声源的强度。

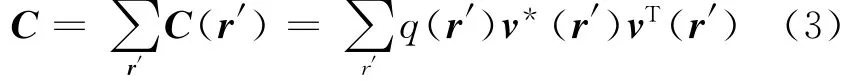
将式（3）代入式（1）得

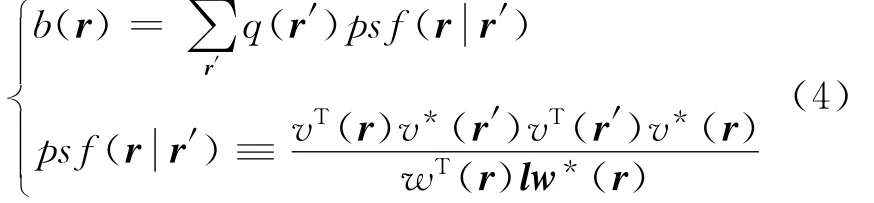
式中：psf（r|r′）为阵列点传播函数，表示r′位置单位强度声源在聚焦点r位置的波束形成贡献量，则聚焦点r位置的波束形成输出量等于各声源在该位置的波束形成贡献量的和，当聚焦点r等于声源点r′时，psf（r|r′）等于1，传统波束形成输出量b（r）等于声源强度q（r′），形成“主瓣峰值”。图1（b）为声源计算平面中心点声源的阵列点传播函数，其在中心聚焦点输出0dB峰值的“主瓣”，在其他聚焦点输出幅值相对较低的“旁瓣”，声源被有效识别。主瓣宽度决定声源识别的分辨率，旁瓣水平影响声源识别准确度。

1.2 DAMAS

DAMAS在传统波束形成输出结果、阵列点传播函数、声源分布之间建立线性方程组

式中：b＝［b（r）］为N维已知列向量；N为聚焦网格点数目；A＝［psf（r|r′）］为N×N维已知阵列点传播函数矩阵；q＝［q（r′）］，q（r′）≥0为N维未知列向量。采用高斯-塞德尔迭代方案求解q，获取声源信息，从而移除阵列点传播函数的影响，有效缩减主瓣宽度、衰减旁瓣，清晰化声源识别结果［10］。初始化q（0）＝0，由第n次迭代计算结果q（n）到第n＋1次迭代计算结果q（n＋1）的步骤为

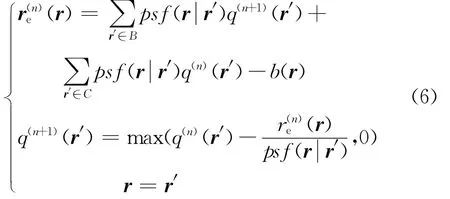
式中：re为残差，B为已完成第n＋1次迭代计算的声源点的集合，C为未进行第n＋1次迭代计算的声源点的集合，B与C的并集为所有声源点的全集。

1.3 DAMAS2

DAMAS2是DAMAS的扩展，其假设阵列点传播函数具有空间转移不变性，即其只取决于观测点与声源点间的相对位置，而与具体位置无关，从而将式（4）示的波束形成输出结果表示为声源分布与阵列点传播函数的卷积，并通过傅里叶变换将其转化为波数域的乘积，如式（7）示，其中，“F”，“F-1”分别为正、逆傅里叶转换算子，psfs为空间转移不变阵列点传播函数，多采用声源计算平面中心位置处点声源的阵列点传播函数。

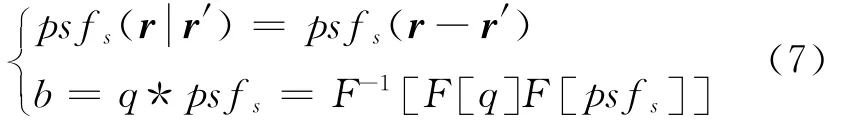
DAMAS2求解q的具体步骤为：

（1）计算（k）＝F［psfs（r）］，这里，k为波数向量，为波数域阵列点传播函数；

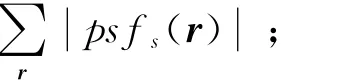
（3）初始化q（0）＝0，采用雅可比迭代方案求解q

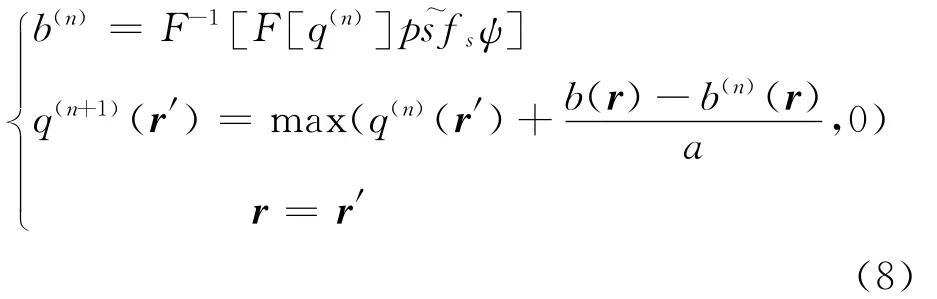
式中ψ为高斯规则化滤波函数，如式（9）所示

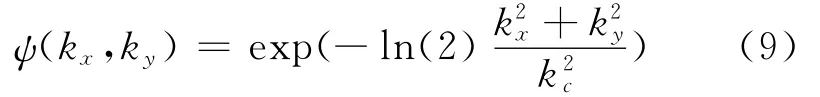
式中：kx，ky分别为x，y方向的波数；kc＝hπ/Δ为滤波器截断波数；Δ为聚焦点间隔；h为常数，常取0.5。高斯规则化滤波函数对光滑声源分布、抑止高波数噪声具有重要作用［11］。

1.4 NNLS

NNLS在传统波束形成输出结果、阵列点传播函数、声源分布之间建立差函数

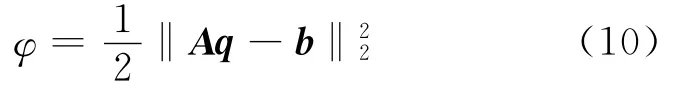
式中：‖‖2表示2范数。最小化该差函数来求解q，获取声源信息，从而移除阵列点传播函数的影响，有效缩减主瓣宽度、衰减旁瓣，清晰化声源识别结果［12］。梯度投影法是求解NNLS问题的常用数学方法，其核心思想是负梯度方向指向标量场下降最快的方向，通过在φ关于q的负梯度方向上按特定步长反复迭代搜索来获取q。初始化q（0）＝0，由第n次迭代计算结果q（n）到第n＋1次迭代计算结果q（n＋1）的具体步骤为：

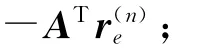
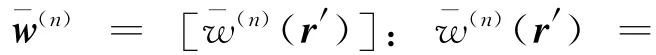
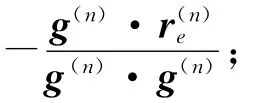
（6）确 定q（n＋1）（r′）＝max（q（n）（r′）＋（n）（r′），0）。

1.5 FFT-NNLS

FFT-NNLS是NNLS的扩展，其与DAMAS2类似，通过假设空间转移不变阵列点传播函数和镜像空间转移不变阵列点传播函数，将NNLS第1，2，4步迭代计算中的大维数矩阵运算转化为傅里叶运算，基于FFT提高求解速度［12］。基于空间转移不变阵列点传播函数，第1，4步的迭代计算可分别写为

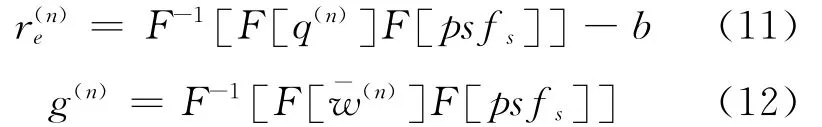
定义镜像空间转移不变阵列点传播函数psf如式（13）所示，第2步的迭代计算可写为残差分布与镜像阵列点传播函数的空间卷积或波数域乘积，如式（14）所示

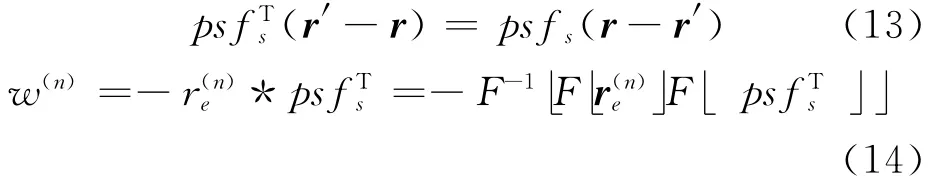
1.6 CLEAN

CLEAN通过反复在传统波束形成结果中移除与主瓣峰值对应的阵列点传播函数来清晰化声源识别结果［13-14］。初始化传统波束形成输出向量b（0）＝b，阵列传声器接收声信号的互谱矩阵D（0）＝C，主瓣峰值所反映的声源强度分布Q（0）＝0，由第n次迭代计算到第n＋1次迭代计算的具体步骤为：

（1）计算传统波束形成输出量

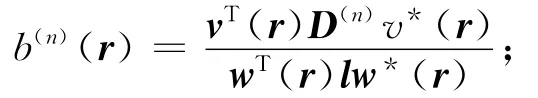
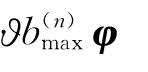
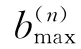
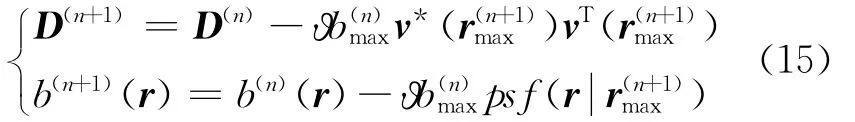
返回第2步重复循环。完成I次迭代计算后，声源强度分布Q＝Q（I）＋b（I）。

1.7 CLEAN-SC

上述5种清晰化方法均需要基于单极子点声源假设计算理论的阵列点传播函数，与这些方法不同，CLEAN-SC基于同一声源产生的主瓣与旁瓣完全相干的原理，通过反复在传统波束形成结果中移除与主瓣相干的旁瓣来清晰化声源识别结果，不需要重构阵列点传播函数［14］。其基本思路与CLEAN类同，不同之处在于第4步重构的传统波束形成输出量是上一循环传统波束形成输出量中与主瓣峰值不相干的部分，有

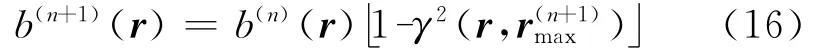
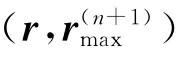
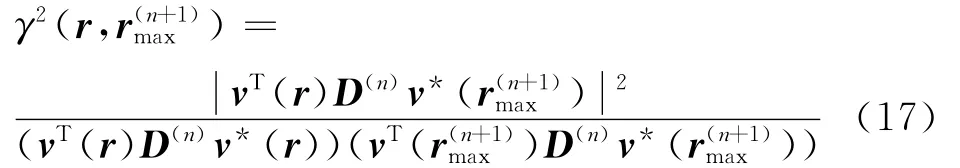
2 模拟计算

基于上述波束形成声源识别结果清晰化方法理论，设计声源识别算法，模拟计算声源计算平面上已知声源的声学成像。该算法包括正向声场模拟、传统波束形成反向声源识别、结果清晰化后处理三部分。首先，在尺寸1m×1m的声源计算平面上建立51×51的聚焦网格点模型并假设点声源分布，在距离声源计算平面1m的位置建立直径0.65m的36通道COMBO传声器阵列测点模型，根据声学原理正向计算阵列各传声器接收的声信号，得其互谱矩阵；然后，反向聚焦各网格点，根据式（2）计算其转向向量，根据式（1）所示的传统波束形成理论，计算其输出量并进行声学成像；最后，分别根据 DAMAS、DAMAS2、NNLS、FFT-NNLS、CLEAN、CLEAN-SC的计算方案，迭代计算声源强度分布并成像，迭代次数均为100次，在CLEAN、CLEAN-SC的循环计算中，设定波束宽度为0.05m，循环因子ϑ＝0.1。

假设单极子点声源位于声源计算平面上（0，0）m位置，声源强度为100dB，辐射声波频率为3 000Hz，图2为模拟计算的识别成像图，显示动态范围为20dB。图2（a）为理论准确值的成像图，其成像量是基于假设的理论声源强度向量q的声压级，其仅在（0，0）m声源位置出现100dB的峰值，其余各聚焦点的幅值均为0。图2（b）为传统波束形成的成像图，其成像量是基于输出量b（r）的声压级，成像图以（0，0）m声源位置为圆心形成半径约为0.2m峰值等于100dB的红色声学中心，声源被有效识别；显示动态范围内，声源计算平面上出现了大面积旁瓣，污染声源识别成像图。图2（c-h）分别为各清晰化方法的成像图，其中，DAMAS，DAMAS2，NNLS，FFT-NNLS成像图的成像量是基于迭代计算的声源强度向量q的声压级，CLEAN，CLEAN-SC成像图的成像量是基于迭代计算的主瓣峰值所对应的声源强度分布Q的声压级，各成像图中均在（0，0）m声源位置出现幅值较高的红色声学中心，声源被有效定位，且这些声学中心的宽度显著窄于图2（b），表明这些清晰化方法均能够显著缩减主瓣宽度、提高声源识别分辨率；显示动态范围内，除了图2（d）在边界出现少量旁瓣外，各图均未见旁瓣干扰，表明这些清晰化方法均能够有效衰减旁瓣。对比图2（c-h），各图中的声学中心宽度和峰值不同，图2（c-f）计算的声源强度分别为93.9dB，87.6dB，89.4dB，89.2 dB，低于理论声源强度，图2（g，h）计算的声源强度均为100dB，等于传统波束形成的主瓣峰值，等于理论声源强度；此外，所花费的计算时间也各不相同，100 次 迭 代 计 算，DAMAS2，FFT-NNLS，CLEAN，CLEAN-SC耗时较短，依次为3，5，8，8 s，DAMAS和 NNLS耗时很长，分别为15，47 min，究其原因主要是因为这两种方法采用大维数的矩阵运算的缘故。

图2的模拟计算结果显示不同波束形成声源识别结果清晰化方法的准确度、计算效率不同，为进一步对比各方法的性能，用式（18）定义的声源强度标准差来衡量准确度，其中，qe为声源强度的准确值，q（n）为第n次迭代计算的声源强度值，对于CLEAN、CLEAN-SC，q（n）（r′）用Q（n）（r′）替代，值得注意的是，这里计算Q（n）（r′）时需设定波束宽度为0，即仅保留主瓣峰值点。

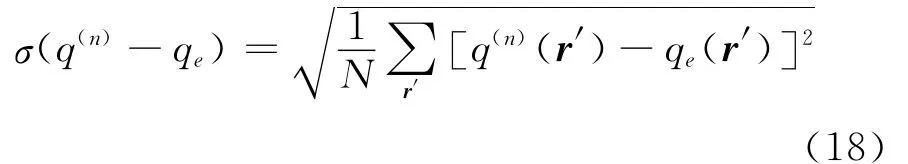
图3为模拟计算的各方法在识别上述单声源时的性能曲线。因为DAMAS，NNLS完成单频的计算就需要数十分钟，解决工程问题需要数十甚至数百小时，工程应用价值不高，所以下文不再进一步探究。图3（a）为声源强度标准差随迭代次数的变化曲线，10～2 000次迭代范围内，各方法的标准差均未超过0.1Pa2，表明各方法均能较准确地重构声源强度信息；DAMAS2，FFT-NNLS的标准差大于0，随迭代次数的增加递减变化，且前者大于后者，CLEAN，CLEAN-SC的标准差在100次迭代时就收敛为0，表明CLEAN，CLEAN-SC的声源识别准确度最高，FFT-NNLS次之，DAMAS2略差，FFT-NNLS，DAMAS2的声源识别准确度随迭代次数的增加而变高。图3（b）为计算时间随迭代次数的变化曲线，四条曲线随迭代次数的增加递增变化，同一迭代次数条件下，DAMAS2耗时最短，FFT-NNLS略短，CLEAN-SC次之，CLEAN略长。

为对比分析各清晰化方法对不相干声源的识别性能，假设不相干双声源分别位于声源计算平面上（0，0）m，（0，0.3）m 位置，声源强度均为100 dB，辐射声波频率均为3 000Hz。图4为模拟计算的识别成像图，显示动态范围为20dB，图4（ae）分别为传统波束形成、DAMAS2，FFT-NNLS，CLEAN，CLEAN-SC的成像图。各图中均在（0，0）m，（0，0.3）m 声源位置出现幅值较高的红色声学中心；图4（b～e）声学中心的宽度显著窄于图4（a）；显示动态范围内，图4（a）在非声源位置出现大面积旁瓣，图4（b，c）仅在很少的非声源位置出现旁瓣，图4（d，e）中未见旁瓣；图4（d，e）的声学中心峰值为100dB，等于理论声源强度，图4（b，c）的声学中心峰值分别为87.8，89.9dB，低于理论声源强度，表明相对于传统波束形成，DAMAS2，FFT-NNLS，CLEAN，CLEAN-SC在识别不相干声源时，均能有效提高分辨率，衰减旁瓣，更准确地识别声源；CLEAN，CLEAN-SC的准确度高于DAMAS2，FFT-NNLS。

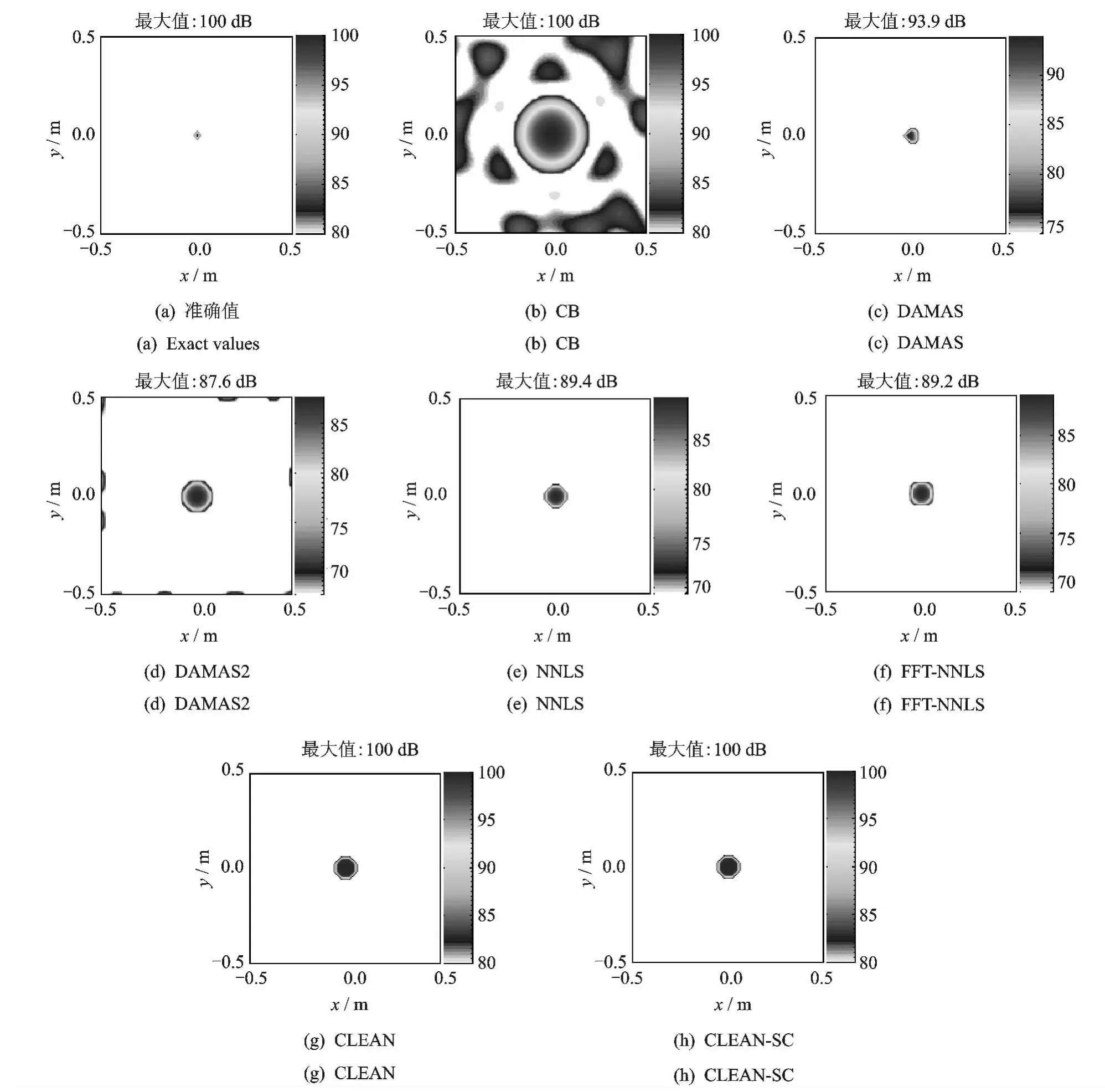
图2 单声源识别成像图Fig.2 Imaging diagrams of single source identification

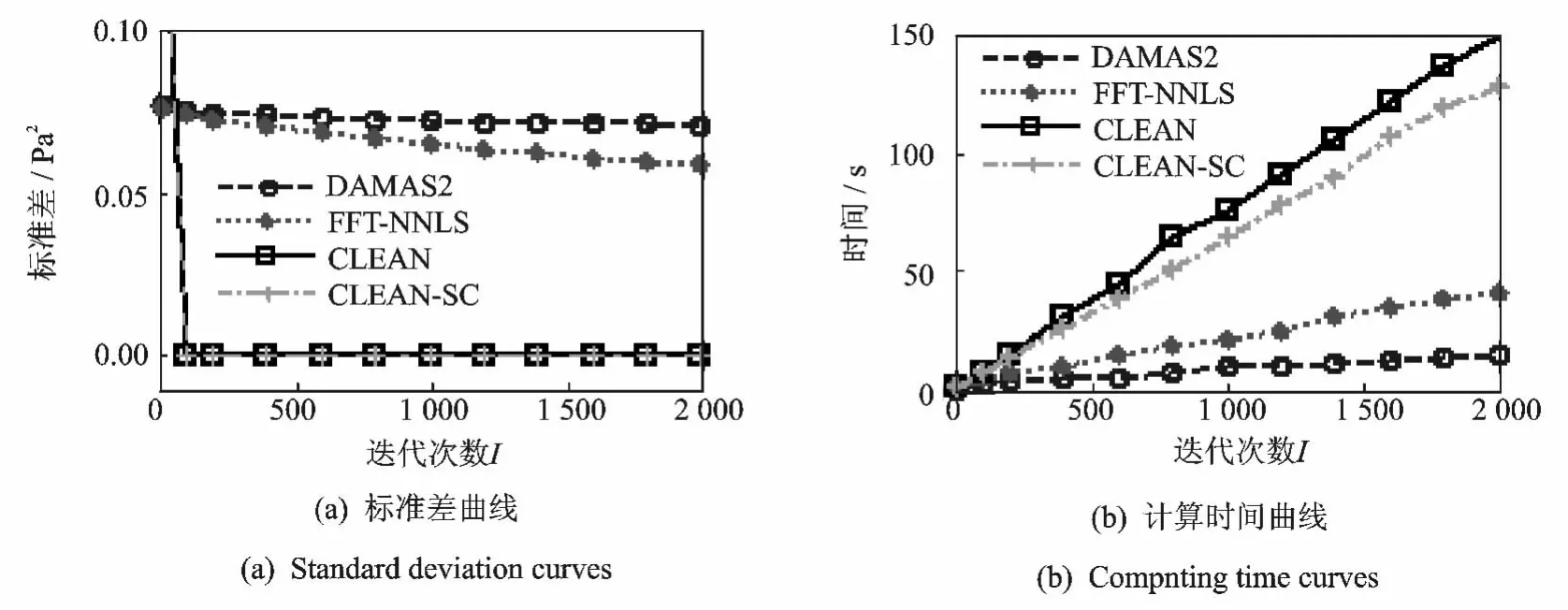
图3 单声源识别性能曲线Fig.3 Performance curves of single source identification

图4 不相干声源识别成像图Fig.4 Imaging diagrams of incoherent sources identification

上述清晰化方法均是基于不相干声源假设建立的，为对比验证其识别相干声源的有效性，假设相干双声源分别位于声源计算平面上（0，0）m，（0，0.3）m位置，声源强度均为100dB，辐射声波频率均为3 000Hz。对于相干声源，阵列传声器接收声信号的互谱由各传声器接收的声信号直接计算，而每个传声器接收的声信号等于各声源在该传声器处产生声信号的和。图5为模拟计算的识别成像图，显示动态范围为20dB，图5（a-e）分别为 传 统 波 束 形 成、DAMAS2，FFT-NNLS，CLEAN，CLEAN-SC的成像图。图5（a-d）中均在（0，0）m、（0，0.3）m 声源位置出现幅值较高的红色声学中心；图5（b-d）声学中心的宽度显著窄于图5（a）；显示动态范围内，图5（a，d）在非声源位置出现大面积旁瓣，图5（b，c）仅在很少的非声源位置出现旁瓣，表明相对于传统波束形成，DAMAS2，FFT-NNLS在识别相干声源时也能有效提高分辨率，衰减旁瓣，更准确地识别声源；CLEAN虽能够提高分辨率，但无法有效衰减旁瓣。图5（e）中仅在（0，0.3）m 声源位置出现幅值较高的红色声学中心，丢失了（0，0）m位置的声源，这主要是因为CLEAN-SC的迭代原理是在传统波束形成输出结果中移除与主瓣相干的旁瓣，（0，0）m位置声源与（0，0.3）m 位置声源相干且后者对应的主瓣峰值略高于前者，从而造成前者对应的主瓣被当成后者的旁瓣被移除的缘故，表明CLEAN-SC无法准确识别相干声源。

3 试验验证

模拟计算是基于点声源假设进行的，实际声源并非简单的点声源，为进一步对比分析各波束形成声源识别结果清晰化方法在识别实际声源时的性能，进行单扬声器、不相干双扬声器、相干双扬声器的声源识别算例试验。试验在进行了声学处理的普通房间内进行，采用相距0.3m由稳态白噪声信号激励的两悬挂扬声器作为声源，采用Brüel＆Kjær公司、0.65m直径、集成4958型传声器的36通道COMBO阵列在距声源平面0.7m的位置接收声信号，各传声器接收的声信号被41通道PULSE3560D型数据采集系统同时采集并传输到PULSE LABSHOP软件中进行频谱分析，得传声器信号的互谱矩阵，试验时，利用Brüel＆Kjær4231型声学校准器对所有传声器均进行了幅值灵敏度校准，采用存储在传声器内的TEDS（数据电子表格）出厂相位数据进行了相位修正，使得校准和修正后的所有传声器自身之间的幅值和相位误差相对于由于传声器之间距离引起的幅值和相位差处于很小的范围内，对最终的传声器信号各互谱函数的影响很小，可以忽略。进一步，基于上述各方法编程实现声源计算平面的声源识别声学成像，这里，设定声源计算平面尺寸为0.6m×0.4m，网格间距为0.025m×0.025m，各清晰化方法的迭代次数均为100，CLEAN，CLEAN-SC设定波束宽度为0.05m，循环因子ϑ＝0.1。

图5 相干声源识别成像图Fig.5 Imaging diagrams of coherent sources identification

图6为3 008Hz仅右侧扬声器被激励时的声源识别成像图，图6（a-e）分别对应传统波束形成、DAMAS2，FFT-NNLS，CLEAN，CLEAN-SC，显示动态范围均为20dB。各图中均在右侧发声扬声器对应位置出现声学中心，声源被有效定位。对比图6（a）与图6（b-e），图6（b-e）中声学中心的宽度显著窄于图6（a）；显示动态范围内，图6（a）在非声源位置出现大面积旁瓣，图6（b-d）仅在很少的非声源位置出现旁瓣，图6（e）中未见旁瓣，表明相比于传统波束形成，DAMAS2，FFT-NNLS，CLEAN，CLEAN-SC在识别单声源时均能够有效提高分辨率，衰减旁瓣。对比图6（b～e），图6（d，e）中声学中心峰值均为53dB，等于传统波束形成的主瓣峰值，即声源强度，图6（b，图6（c）中声学中心峰值分别为44，45dB，低于声源强度；显示动态范围内非声源位置出现的旁瓣在图6（b）最多，图6（c）中次之，图6（d）中较少，图6（e）中没有，表明对单声源的识别准确度CLEAN-SC最好，CLEAN次之，FFT-NNLS略差，DAMAS2最差。该规律与模拟计算结果略有不同：模拟计算中CLEAN，CLEAN-SC的成像结果一致，算例试验中CLEAN-SC的性能优于CLEAN，究其原因主要是因为CLEAN的迭代原理是在传统波束形成输出结果中移除基于单极子点声源假设重构的主瓣峰值声源的阵列点传播函数，算例试验中的扬声器声源并非简单的点声源，其传统波束形成输出结果并不简单等于其声源强度与式（4）所示的基于单极子点声源假设理论重构的阵列点传播函数的乘积，该系统误差是造成CLEAN在识别实际声源时性能下降的关键，而模拟计算是基于点声源假设进行，不存在该系统误差。实际声源因不满足点声源假设而带来的系统误差是造成以阵列点传播函数为基础的DAMAS2，FFT-NNLS，CLEAN方法性能低于CLEAN-SC的重要方面。

图7为3 008Hz左右扬声器分别被两不相干信号激励时的声源识别成像图。图7（a-e）分别对应 传 统 波 束 形 成、DAMAS2，FFT-NNLS，CLEAN，CLEAN-SC，显示动态范围均为20dB。各图中均在两发声扬声器对应位置出现声学中心；图7（b-e）中声学中心的宽度显著窄于图7（a）；图7（d，e）中声学中心峰值均为53dB，等于图7（a）的主瓣峰值，即声源强度，图7（b，c）中声学中心峰值分别为44，45dB，低于声源强度；显示动态范围内，图7（a）在非声源位置出现大面积旁瓣，图7（b-d）仅在很少的非声源位置出现旁瓣，图7（e）中未见旁瓣，表明相比于传统波束形成，DAMAS2，FFT-NNLS，CLEAN，CLEAN-SC在识别不相干声源时均能够有效提高分辨率，衰减旁瓣，CLEAN-SC的准确度最好，与单扬声器声源的识别结果一致。

图6 单扬声器声源识别成像图Fig.6 Imaging diagrams showing identification results of single loudspeaker source

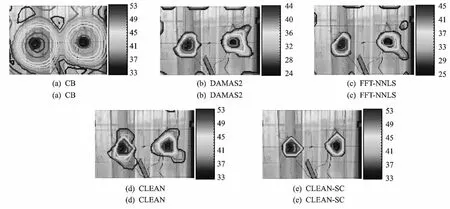
图7 不相干扬声器声源识别成像图Fig.7 Imaging diagrams showing identification results of incoherent loudspeaker sources

图8为3 008Hz左右扬声器均被同一信号激励时的声源识别成像图，图8（a-e）分别对应传统波束 形 成、DAMAS2，FFT-NNLS，CLEAN，CLEAN-SC，显示动态范围均为20dB。图8（a-d）中均在两发声扬声器对应位置出现声学中心；图8（b～d）声学中心的宽度显著窄于图8（a）；显示动态范围内，图8（a，d）在非声源位置出现大面积旁瓣，图8（b，c）仅在很少的非声源位置出现旁瓣，表明相对于传统波束形成，DAMAS2，FFT-NNLS在识别相干声源时能够有效提高分辨率，衰减旁瓣，更准确地识别声源；CLEAN虽能够提高分辨率，但无法有效衰减旁瓣。图8（e）中左侧扬声器位置出现幅值较高的红色声学中心，右侧扬声器位置声源强度幅值显著降低，仅约34dB，与实际严重不符，表明CLEAN-SC无法准确识别相干声源。上述规律与模拟计算结果一致。

图8 相干扬声器声源识别成像图Fig.8 Imaging diagrams showing identification results of coherent loudspeaker sources

4 结 论

本文阐明 DAMAS，DAMAS2，NNLS，FFTNNLS，CLEAN，CLEAN-SC清晰化方法的基本原理，模拟计算声源平面上已知声源的识别成像图及性能曲线，进行人为设计的扬声器声源的识别算例试验，对比分析各方法的成像规律和性能。主要结论如下：

（1）针对已知单声源的仿真模拟耗时统计表明：DAMAS2计算效率最高，FFT-NNLS次之，CLEAN，CLEAN-SC略低，DAMAS，NNLS很低，计算效率差的局限性限制了DAMAS与NNLS的工程应用价值。

（2）针对已知单声源、不相干声源的仿真模拟和算例试验表明：相比于传统波束形成，DAMAS2，FFT-NNLS，CLEAN，CLEAN-SC均能有效衰减旁瓣，显著提高分辨率，更准确地识别声源；CLEAN-SC的识别准确度最高，CLEAN，FFT-NNLS次之，DAMAS2略差。

（3）针对已知相干声源的仿真模拟和算例试验表明：对于相干声源，DAMAS2，FFT-NNLS能有效衰减旁瓣，显著提高分辨率，识别准确度高；CLEAN能提高分辨率，但不能有效衰减旁瓣；CLEAN-SC会造成部分声源信息丢失，无法准确识别相干声源。

［1］陈志菲，孙进才，侯宏.基于奇异值分解的方向估计改进方法［J］.数据采集与处理，2011，26（5）：499-502.

Chen Zhifei，Sun Jincai，Hou Hong.Modified method for bearing estimation based on singular value decomposition ［J］.Journal of Data Acquisition and Processing，2011，26（5）：499-502.

［2］Mehdi Batel，Marc Marroquin.Noise source location techniques—Simple to advanced applications ［J］.Journal of Sound and Vibration，2003，37（3）：24-38.

［3］褚志刚，杨洋，蒋忠翰.波束形成传声器阵列性能研究［J］.传感技术学报，2011，24（5）：665-670.

Chu Zhigang，Yang Yang，Jiang Zhonghan.Study on the beamforming performance of microphones array［J］.Chinese Journal of Sensors and Actuators，2011，24（5）：665-670.

［4］褚志刚，杨洋.近场波束形成声源识别的改进算法［J］.农业工程学报，2011，27（12）：178-183.

Chu Zhigang，Yang Yang.Improved algorithm of nearfield beamforming for sound source identification ［J］.Transactions of the CSAE，2011，27（12）：178-183.

［5］褚志刚，杨洋，王卫东，等.基于波束形成方法的货车车外加速噪声声源识别［J］.振动与冲击，2012，31（7）：66-70.

Chu Zhigang，Yang Yang，Wang Weidong，et al.I-dentification of truck noise sources under passby condition based on wave beamforming method［J］.Journal of Vibration and Shock，2012，31（7）：66-70.

［6］杨洋，褚志刚，倪计民，等.除自谱的互谱矩阵波束形成噪声源识别算法研究［J］.噪声与振动控制，2011，31（4）：145-148.

Yang Yang，Chu Zhigang，Ni Jimin，et al.Research on algorithm of sound source identification based on cross-spectral beamforming with exclusion of autospectra ［J］.Noise and Vibration Control，2011，（4）：145-148.

［7］杨洋，倪计民，褚志刚，等.基于互谱成像函数波束形成的发动机噪声源识别［J］.内燃机工程，2012，33（3）：82-87.

Yang Yang，Ni Jimin，Chu Zhigang，et al.Noise source identification of an engine based on cross-spectra imaging function beamforming［J］.Chinese Internal Combustion Engine Engineering，2012，33（3）：82-87.

［8］李静，陈华伟.基于正则化约束最小二乘的稳健频率不变波束形成器设计方法［J］.数据采集与处理，2012，27（2）：202-209.

Li Jing，Chen Huawei.Robust FIB design using regularized constrained least squares［J］.Journal of Data Acquisition and Processing，2012，27 （2）：202-209.

［9］Yardibi T，Bahr C，Zawodny N，et al.Uncertainty analysis of the standard delay-and-sum beamformer and array calibration［J］.Journal of Sound and Vibration，2010，329（13）：2654-2682.

［10］Thomas F Brooks，William M Humphreys.A deconvolution approach for the mapping of acoustic sources（DAMAS）determined from phased microphone arrays［R］.AIAA-2004-2954，USA：AIAA，2004.

［11］Robert P Dougherty.Extensions of DAMAS and benefits and limitations of deconvolution in beamforming ［R］.AIAA-2005-2961，USA：AIAA，2005.

［12］Klaus Ehrenfried，Lars Koop.Comparison of iterative deconvolution algorithms for the mapping of acoustic sources［J］.AIAA Journal，2007，45（7）：1584-1595.

［13］Schwarz U J.Mathematical-statistical description of the iterative beam removing technique（method CLEAN）［J］.Astronomy and Astrophysics，1978，65：345-356.

［14］Sijtsma P.CLEAN based on spatial source coherence［J］.International Journal of Aeroacoustics，2007，6（4）：357-374.