Hilbert-Huang变换在T型输电线路故障定位中的应用

李志斌，吴宝兴，许云辉

（上海电力学院电力与自动化工程学院，上海200090）

Hilbert-Huang变换在T型输电线路故障定位中的应用

李志斌，吴宝兴，许云辉

（上海电力学院电力与自动化工程学院，上海200090）

根据T型线路故障时各端测得的行波波头到达时刻来建立判别矩阵，以此来判断故障支路。将单端与双端定位方法相结合，解决了T型线路交汇点附近(小于1 km)故障支路难以判断的问题。针对Hilbert-Huang变换过程中经验模式分解(EMD)处理数据时可能造成端点效应和模态混叠，提出使用白噪声聚类经验模型分解(EEMD)以及一种改进的EMD算法来代替，用分解前后信号的总能量来评估几种分解过程的准确性。定位结果表明EEMD以及改进的EMD算法在T型线路故障定位中的定位精度高于EMD算法，能满足定位的输电线路的定位精度要求。

T型输电线路；Hilbert-Huang变换；故障定位

高压输电线路发生故障时，快速准确地找出故障位置对提高电网供电可靠性和运行稳定性具有重要意义。行波定位法利用输电线路故障时会产生向两端运动的暂态行波实现故障定位，能够很好地解决故障类型和过渡阻抗对定位精度的影响，但是暂态行波持续时间短、衰减严重，难以检测[1]。小波分析方法能准确提取故障行波波头，但小波分析需要根据线路的参数选取最适合的小波基，否则会影响行波波头到达时刻的准确测定[2-3]。Hilbert-Huang变换(HHT)是近年来出现的自适应信号分析方法，它分为经验模式分解(empiricalmode ecomposition，EMD)和Hilbert谱分析(Hilbert spectrum analysis，HAS)两部分。HHT变换根据信号进行自适应分解，基函数自适应地在分解过程中产生，解决了小波变换中基函数的选取问题[4]。

1 Hilbert-Huang变换

1.1 EMD算法

EMD算法是利用信号极值点来提取各固有模态分量(IMF)，其结果是将信号中真实存在的不同尺度的波动或趋势逐级地由高频至低频分解开。在故障发生时刻会使频谱图上出现高频突变，以此来确定行波波头到达时刻[5]。

EMD的分解结果可以表示为：

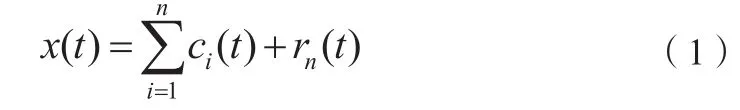
在EMD分解过程中，会由于“筛选”过程中进行均值计算的包络拟合函数在数据序列的两端出现发散的现象，这种发散现象会随着“筛选”过程的进行而传播到数据序列内部，导致EMD分解失真[6-7]。

1.2 改进的EMD算法

针对EMD算法可能出现的端点效应，利用端点附近的两个相邻极值点(极大值，极小值)斜率相等这一特性，在端点处定义两个极值点，分别连接相邻的极大值与极小值，然后对包络线进行拟合。端点极值分布总共有如下四种情况：

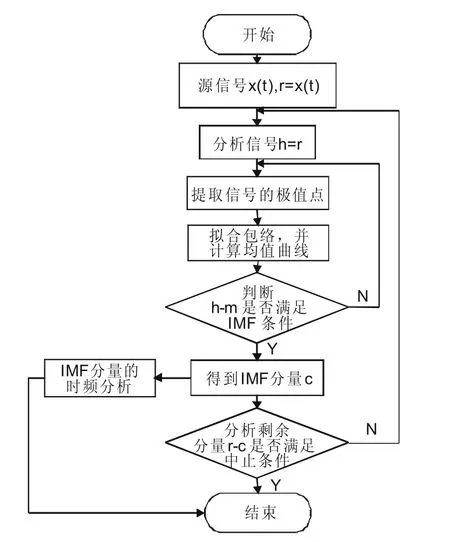
图1 EMD算法流程图

(3)最后一个极值是极大值；

(4)最后一个极值是极小值。

情况(1)、(2)如图2、图3所示，情况(3)、(4)定义极值点的过程同理。

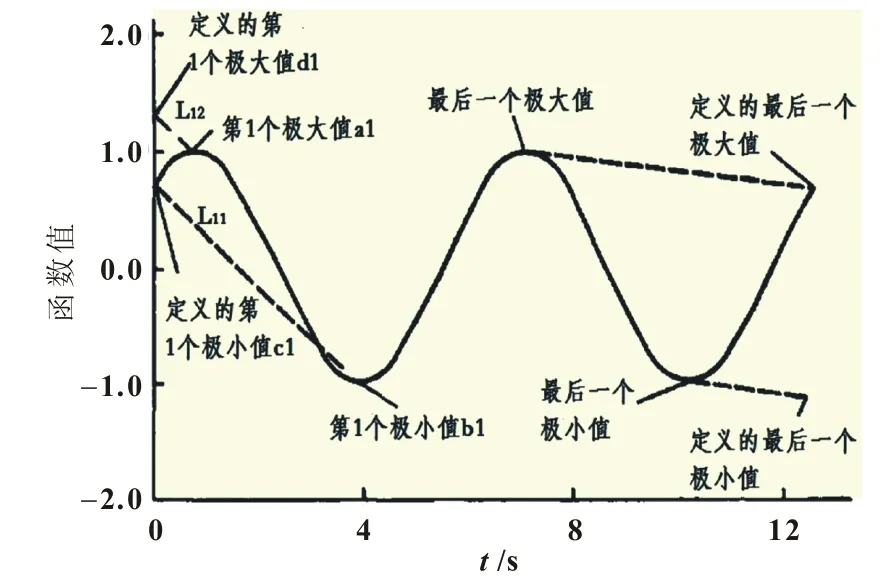
图2 第一个极值为极大值的端点极值定义

1.3 EEMD算法

EEMD是针对EMD方法的不足而提出的一种噪声辅助数据分析方法。EEMD分解原理为：当附加的白噪声均匀分布在整个时频空间，该时频空间就由滤波器组分割成的不同尺度成分组成。当信号加上均匀分布的白噪声背景时，不同尺度的信号区域将自动映射到与背景白噪声相关的适当尺度上去[8]。

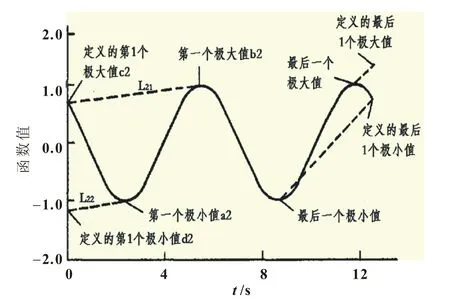
图3 第一个极值为极小值的端点极值定义

(1)给目标信号加上一组白噪声获得一个总体；

(2)对其进行EMD分解，得到各IMF分量；

(3)给目标信号加入不同的白噪声，重复以上两步；

(4)分解得到各自的IMF分量组；

(5)取相应IMF的均值作为最终的IMF组；

(6)取相应的剩余分量的均值作为最终的IMF组。

1.4 评价标准

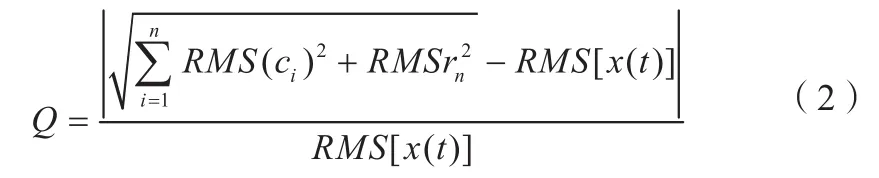
2 T型线路行波法定位

行波故障定位法是根据行波传输理论，以行波在线路上传输速度接近光速为基础，利用不同的模型原理来确定故障点。T型线路模型如图4所示。T型输电线路的故障测距由两部分组成：一是故障分支的判别，二是故障点测距。

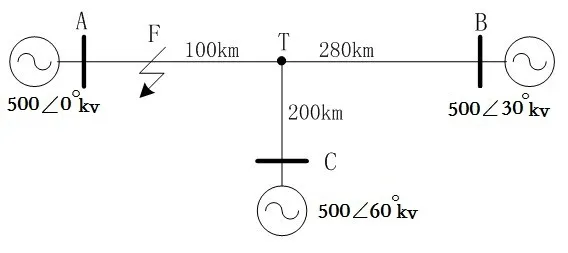
图4 T型线路模型

2.1 T型线路故障支路判断

构造时间矩阵=[AB,AC,BC]，根据线路参数计算得=[614.7,341.5,－273.2]。当T型线路发生故障时，A、B、C三端记录故障初始行波到达时间为A′,B′,C′以此得到时间矩阵′=[AB′,AC′,BC′]。由上述分析得，时间矩阵,′中非故障支路对应的ij与ij′相等；T点故障时，时间矩阵,′相等。构造判断矩阵：=－′=[AB－AB′,AC－AC′,BC－BC′]。

2.2 T型线路行波定位法步骤

在故障分支判定环节完成后，接下来则需要对故障点的具体位置进行精确定位。影响测距精度的关键要素之一是行波速度，而实际的行波速度会受到输电线路参数、地理环境及气候条件等众多因素的影响，导致行波速度具有不确定性。在三端故障测距中，利用迭代得到式(3)，可以消除测距公式中行波速度的影响，在一定程度上消除弧垂带来的误差。

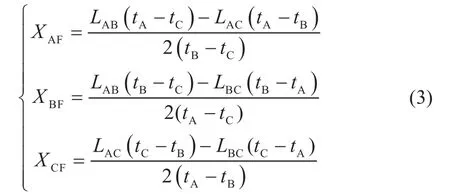
但是由于行波波头到达时刻的测定存在误差，实际定位中式(3)可能会造成某些点有较大的误差，因此该方法有一定的局限性。本文在定位过程中近似认为行波波速为一常数[10]。

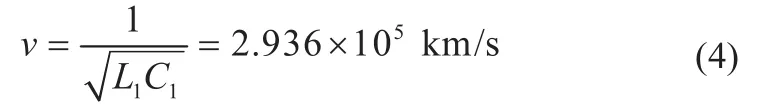
假设各端时间同步[11-12]，则能够获得初始行波浪涌到达三母线测量端的绝对时刻A，B，C，采用双端定位法定位故障位置步骤如下：

(1)对线路两端采集的行波信号进行相模变换，得到相模分量[13]；

(2)对相模分量进行HHT变换，测得高频突变点位置进而确定行波波头到达各端时刻A，B，C，；

(4)根据判断出的故障支路（假设为AT支路），利用双端定位公式(其中为B、C)分别计算AB和AC两线路的故障位置，取均值实现故障定位。

3 仿真分析

选用京津唐500 kV输电线路的实际参数[14]，采样频率为1 MHz，每千米线路结构参数如下：1=0.02083Ω，1=0.8984mH，1=0.01291 μF，0=0.1148Ω，0=2.2886mH，0=0.00523 μF。

故障点设置：

(1)AT支路1～10 km以1 km为步长取10个故障点，设为A区间；15～85 km，以5 km为步长取15个故障点，设为B区间；90～99 km以1 km为步长取10个故障点，设为C区间；

(2)BT、CT支路A、C区间设置与AT支路一致，B区间由于线路长度不同，分别以20 km为步长取13和9个故障点。

根据T型线路的定位步骤对各支路设置的故障点进行故障仿真，得到故障定位结果如表1所示。

在靠近T点处，时间矩阵中元素接近于零故无法判断故障支路，上述定位步骤无法实现，因此采用单端定位法作为辅助进行故障定位。靠近T节点故障的网格图如图5所示，省略部分T节点相关的反射和折射波。

以AT支路故障为例，利用EEMD算法对该定位方法进行说明。图6为利用EEMD算法定位时各端测得行波波头的到达时刻（=400m）。

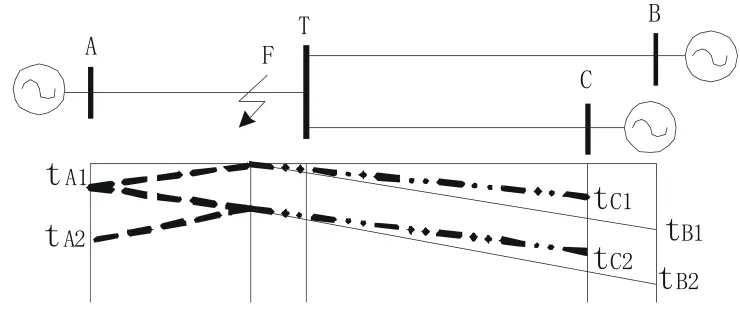
图5 T节点附近(AT段)故障行波网格图

结合行波网格图和EEMD算法时频图中频变确定的行波波头到达时刻，并且计算得到判断矩阵=[－1.3,－1.5,－0.2]，中元素均小于设置的裕度4 μs，近似于0故无法判断故障支路。因此以单端定位法为辅助，利用第二个到达测量端的行波波头进行故障定位。靠近T节点的分析结果如表2所示（A为距A端的距离，由于线路结构造成测得的某些端的行波波头时刻无法用于计算故障位置以及经过验算排除后的结果，在表格中以“——”表示），其中AT支路100 km，BT支路280 km，CT支路200 km。

表2 T节点附近(＜1 km)故障定位结果

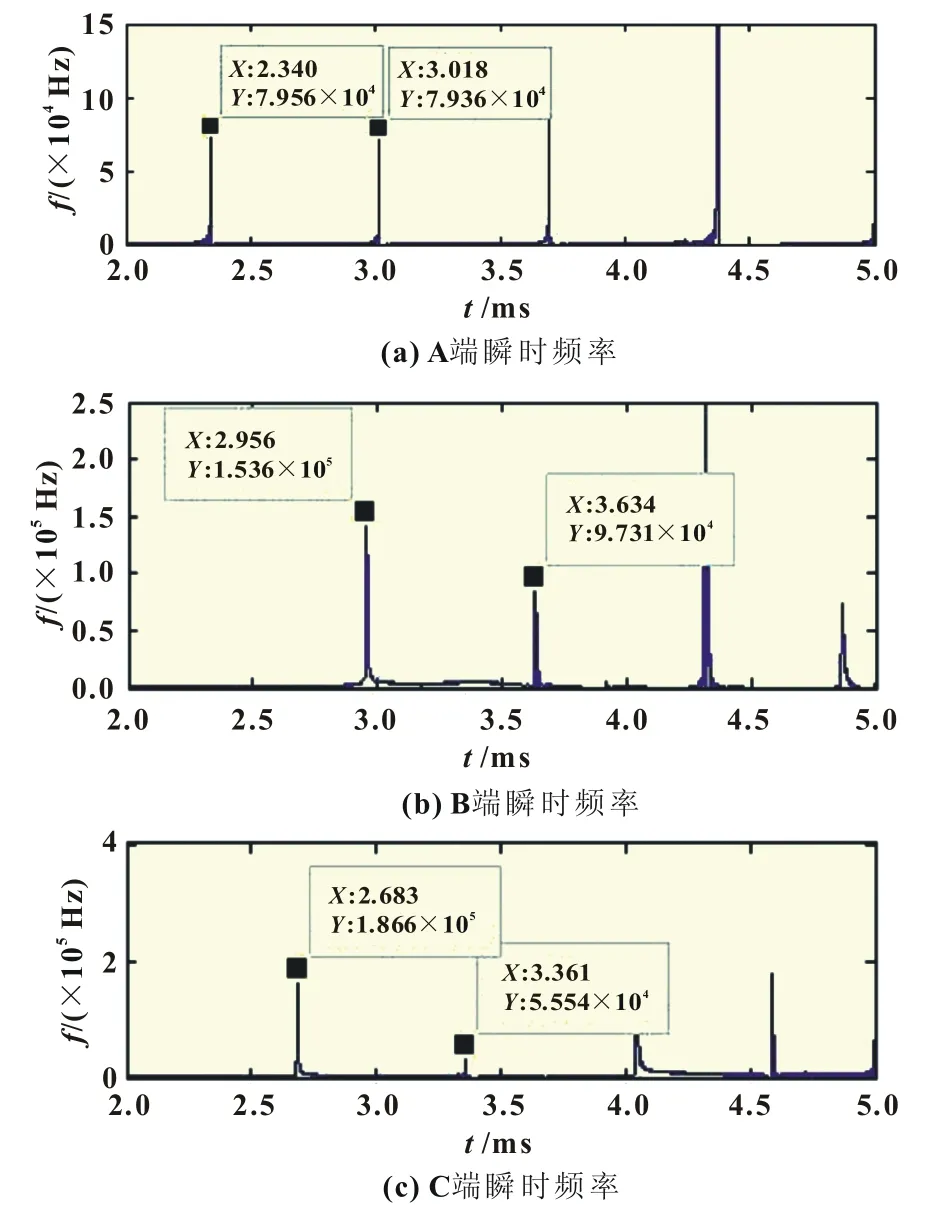
图6 EEMD算法定位结果

表2说明以单端定位法作为辅助，能够很好地解决靠近T节点无法准确判断故障支路的问题，故障精度能够满足定位要求。

4 总结

本文根据T型线路故障时各端测得的行波波头到达时刻来建立时间矩阵，以此来判断故障支路；并将单端与双端定位方法相结合，解决矩阵在靠近T节点时无法准确判断故障支路的问题。针对Hilbert-Huang变换过程中EMD处理数据时可能造成端点效应和模态混叠，提出使用EEMD分解以及一种改进的EMD算法来代替，用分解前后信号的总能量来评估几种分解过程的准确性。定位结果表明EEMD和改进EMD算法在T型线路故障定位中的分解过程更加准确，定位精度更高，能满足定位的输电线路的定位精度要求。

[1]IZYKOWSKI J,ROSOLOWSKI E,SAHA M M,et al.A fault-locationmethod for application with current differential relays of threeterminal lines[J].IEEE Transactions on Power Delivery,2007,22 (4):2099-2107.

[2]王学峰，周俊宇.用小波变换技术定位输电线路故障[J].高电压技术，2006，32(1)：84-87.

[3]李加波，于瑞红，戴玉松，等.基于小波变换的输电线路行波测距研究[J].湖南电力，2005(1)：15-19.

[4]李天云，赵妍，李楠.基于EMD的Hilbert变换应用于暂态信号分析[J].电力系统自动化，2005，29(4)：49-52.

[5]束洪春，程春和，赵文渊.形态学与HHT检测相结合的行波波头准确标定方法[J].电力自动化设备，2009，29(7)：1-7.

[6]刘文钊.Hilbert-Huang变换理论与应用研究[D].长沙：国防科学技术大学，2009.

[7]赵娜.HHT经验模式分解的周期延拓方法[J].计算机仿真，2008，25(12)：346-350.

[8]陈可，李野，陈澜.EEMD分解在电力系统故障信号检测中的应用[J].计算机仿真，2010，27(3)：263-266.

[9]任达千，吴昭同，严拱标.EMD端点效应的评价指标及抑制端点效应的窗函数法[J].制造业自动化，2007，29(1)：21-24.

[10]覃剑，葛维春，邱金辉，等.影响输电线路行波故障测距精度的主要因素分析[J].电网技术，2007，31(2)：28-33.

[11]刘劲，孙扬生，罗毅.一种基于时间域的实用单侧电量故障测距方法[J].电力系统自动化，1994，18(5)：52-56.

[12]POPOVIC L M.A digital fault location algorithm taking into account the imaginary part of the grounding impedance at the fault place[J].IEEE Trans on Power Delivery,2003,18(4)：1489-1496.

[13]宋国兵，李森，康小宁.一种新相模变换矩阵[J].电力系统自动化，2007，31(14)：57-60.

[14]毛鹏，张兆宁，苗友忠，等.基于双端电气量的输电线路故障测距的新方法[J].继电器，2000，28(5)：25-27.

Applied research of improved Hilbert-Huang transform in fault location of T-type transmission line

LI Zhi-bin，WU Bao-xing，XU Yun-hui

The timematrix F according to the transient traveling wave's arrival time to each ends could be used to establish the distinguishmatrix D.The fault slip could be determined.Taking the single-end and double-end locationmethods into connection,the problem of the fault slip near the point of intersection(less than 1km)could be determined.In the process of the Hilbert-Huang transform,empiricalmode decomposition(EMD)may result in the end effect andmodal aliasing when processing data.Ensemble Empirical Mode Decomposition(EEMD)was proposed.The EMD was substituted by an improved EMD.The accuracy of the decomposition processes according to the total energy of the signal before and after the decomposition was assessed.Positioning results show that EEMD and improved EMD are better than EMD in the fault location of T-type transmission line,and the positioning accuracy canmeet the requirement of fault location.

T-type transmission line;Hilbert-Huang transform;fault location

TM 74

A

1002-087 X(2014)10-1933-04

2014-03-12

上海市电站自动化技术重点实验室项目

李志斌(1974—)，男，山西省人，副教授，硕士生导师，主要研究方向为故障诊断、测控技术及软件编程。