对ECC的小整数n阶点进行选择明文攻击*

熊莉英 ，李慧云 ，李家会

(1.西南科技大学 信息工程学院，四川 绵阳621010；2.中国科学院深圳先进技术研究院集成技术研究所，广东 深圳518055)

与对称密钥密码体系相比，公钥密码体系允许更灵活的密钥管理。目前，应用最广泛的两种公钥密码算法是RSA以及椭圆曲线密码(ECC)算法[1-2]。与RSA相比，ECC具有更短的密钥长度、更快的运算(诸如内存、能量消耗以及带宽存储)，从而在学术与工程领域引起持续增长的兴趣。

侧信道分析(如时序、功耗、电磁辐射)攻击已经对公钥密码体制的硬件实现产生了威胁。简单功耗分析SPA(Simple Power Analysis)攻击已被证明可有效攻击一些公钥密码算法[3]。该技术主要涉及对运行公钥加密算法的设备功耗进行检查分析。RSA实现中的模方和模乘运算是可以被区分开的，使得对方可以获得密钥。ECC中点加和倍点操作类似于RSA中的模方和模乘操作。如果可以区分ECC实现中的点加和倍点操作，那么攻击者就可以获取ECC密钥。

目前大多数的RSA算法都使用相同的序列进行模乘和模方操作，大多数ECC算法也使用相同的序列进行点加和倍点运算，这增大了对差异的区分难度。RSA中“一贯的模乘和模方操作”以及ECC中“一贯的点加和倍点操作”似乎成为了对抗SPA攻击的有效手段。为了从功耗波形中获得更强的信息泄露，针对特殊输入数据的RSA的选择明文攻击方法得以提出[4-7]，以及采取更为复杂的原子化平衡操作[9]和蒙哥马利方法[10]等，但都使得在SPA攻击时得不到点加和倍点运算的显著功耗变化。

为了在功耗波形中获得增强的信息泄露，本文提出了一种针对ECC算法的选择明文侧信道攻击方法，该方法利用了2阶或者其他小整数阶点作为特殊输入点P，以增强点和倍点操作中的显著变化。

1 ECC概述

1.1 椭圆曲线

ECC算法把现有的离散对数问题转化为椭圆曲线上的连续问题。一个生成元为g的n阶循环群G的离散对数问题指的是找出群G上使y=gx成立的x。椭圆曲线上的离散对数比其他有限域上的群(诸如乘法群)要困难得多。令E(EP)为一个定义在有限域FP上的椭圆曲线，令P为一个E(EP)上的点。素数p、椭圆曲线方程FP、点P以及其阶数n是公共的域参数。私钥是一个从区间[1，n-1]上均匀随机选取的整数d，其相应的公钥是Q=dP。私钥d的确定问题就是椭圆曲线上的离散对数问题(ECDLP)。

椭圆曲线就是由满足定义在F上的Weierstrass方程：

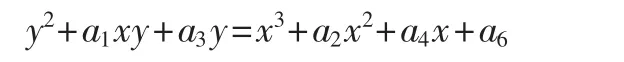
其中ai∈F，这些解的点组成一个平面曲线。如果F的特征值(char)F≠2，3，Weierstrass方程可变成y2=x3+ax+b，a，b∈F。椭圆曲线上的所有点加上一个特殊的无穷远点O，可以由下面给出的加法运算构成一个阿贝尔群结构，当F≠2，3 时的加法方程式：令点P=(x1，y1)≠O，-P=(x1，-y1)。令点Q=(x2，y2)≠O且Q≠-P， 则和P+Q=(x3，y3)可 计算如 下：

其中，

如果P≠Q，则运算P+Q称为点加运算(A)；如果P=Q则该运算称为倍点运算(D)，显然，二者在方程中是不同的。图1说明了ECC的点和倍点运算。

图1 ECC中的点和倍点运算

1.2 ECC算法ECIES-1简介

依据 IEEE P1363a/D9和 ANSI X9．63-2001，公钥加解密算法ECIES-1描述如下：椭圆曲线E的基点为G，阶为n，解密者 B的公钥为点PB=[d]G，私钥为d，M为1 bit的待加密信息。KDF为密钥派生函数，MAC为消息认证码算法，p1、p2为加密者与解密者预先共有的填充码，M为明文。

(1)加密算法

为了对明文M进行加密，作为加密者的用户A进行以下操作：

①随机产生u∈[1，n-1]，计算V=(x，y)=[u]PB。

②计算R=[u]G。

③计算K=KDF(V，p1)=K1||K2。其中K1的长度为 1 bit，K2的长度为k2 bit。

④计算C=M⊗K。

⑤计算T=MACK2(C||p2)。

⑥发送(R，C，T)给用户 B。

(2)解密算法

为了对密文C进行解密，作为解密者的用户B执行以下操作：

①计算V=(x，y)=[d]R。

②计算K=KDF(V，p1)=K1||K2。其中K1的长度为 1 bit，K2的长度为k2 bit。

③计算T′=MACK2(C||p2)，若T′≠T则报错退出，否则继续。

④计算M=C⊗K，M即为恢复出的信息。

1.3 椭圆曲线阶的理论分布情况

点P的阶数指的是满足[n]P=0的最小正整数n，具有如下性质：

定理 1(Hasse定理)：设E(Fq)是定义在域Fq上的椭圆曲线，E(Fq)上点的个数用 #E(Fq)表示，则：

2 攻击ECC的选择消息SPA二进制算法

由于目前绝大多数的标量乘法都采用相同的指令序列来进行点和倍点运算，因此在SPA攻击中，点和倍点的区别不是很明显。为了从功率波中获得更强的信息泄露，而提出采用特殊输入数据的选择消息ECC攻击法。这个方法的基本概念是采用特殊的输入数据，例如阶数为2、3或更小的点P。点P的阶数指的是满足[n]P=0的最小正整数n。为了找到阶数为2的点，令 2P=0，即P=-P。如果P=(x，y)，则-P=(x，-y)。当P=-P，则有y=0。因此选择接近x轴的点(本文中记为Px)来增强点和倍点操作的差别。如点Q=2Px的倍点运算会产生一个接近无穷大的点，也即坐标值(xQ，yQ)非常大，这样就会产生显著的功耗。本文把这种接进无穷大的点Q记为Q∞。

根据从右至左的二进制算法，点加和倍点操作可以归纳为 3种类型：点加（A），点加后倍点（D1）和倍点后的倍点（D2）。由方程式“P+Q”可知，D2操作比 D1或者A操作产生更大的功耗。由此可见，即使原子化防御措施对标量乘实现中的点加和倍点操作进行了功率平衡，如图2所示，所选择的特殊输入点P仍然会使得操作D2与D1和A相比能显著也区分开来。以2阶输入点P为例，由于 2P=O，则有：

因为D2仅在正处理的密钥位为“0”时出现，所以通过SPA就可以确定密钥位的顺序。

该方法通过选择特殊的阶数为2的输入点P，放大了点倍与点加操作的功耗差。通过该方法，可以对ECC实现中的从左至右或从右至左二进制算法进行有效攻击。

图2 特殊选择的接近X轴的输入点P的点和倍点运算

如果输入点P的阶数为3，则具有连续两位1的密钥操作，如下例所示。但Q=3P=O时，功耗波形与其他操作有显著差异，能够被识别出。

或者，具有…1001…的密钥位形式，也能够被识别出。同理，还有如下所示的其他组合。只要出现nP=O，结合前后的功耗波形，就能判断出相邻2或更多位的逻辑值。

3 攻击步骤

为了应用上述的选择消息攻击方法，攻击者应按照下面的步骤进行操作：

(1)确认该椭圆曲线上存在阶数为小整数的点；

(2)证明有阶数为小整数的点存在；

(3)找到该拐点；

(4)进行选择明文攻击。

为了找到阶数为 2的点，令 2P=O(即 P=-P)。如果P=（x，y），则-P=（x，-y）。 当 P=-P 时，有 y=0，即该点 P就是阶数为2的点，存在于x轴上。

要在椭圆曲线y2=x3+ax+b上找到阶数为3的点，令3P=O，则 2P=-P：

由倍点公式可得：

如果 2 P1=-P1，则有：

或者：

则有：

因此，该阶数为3的点在x轴上的值为：

寻找其他阶数点的方法可以进一步阅读参考文献[10-12]。

本文提出了一种新的选择明文的简单功耗分析攻击法。在该方法中，选择阶数为2或者其他小整数阶点作为特殊点P，是为了利用其在无限域上的特殊性。该方法放大了点倍与点加操作的功耗差。通过该方法，可以对ECC实现中的从左至右或从右至左二进制算法进行有效攻击。

[1]MILLER V S.Use of elliptic curves in cryptography[C].Advances in Cryptology，CRYPTO’85 Proceedings，1986，218：417-426.

[2]KOBLITZ N.Elliptic curve cryptosystems[J].Mathematics of Computation，1987，48(177)：203-209.

[3]KOCHER P，JAFFE J，JUN B.Timing attacks on implementations of Diffie-Hellman，RSA，DSS，and other systems[C].Proceedings of 16th International Advances in Cryptology Conference，CRYPTO’96，1996，1109：104-113.

[4]MIYAMOTO A，HOMMA N，AOKI T，et al.Enhanced power analysis attack using chosen message against RSA hardware implementations[C].IEEE Intrnational Symposium on Circuits and Systems，ISCAS 2008，2008：3282-3285.

[5]NOVAK R.SPA-based adaptive chosen-ciphertext attack on RSA implementation[C].International Workshop on Practice and Theory in Public Key Cryptography，LNCS，2002，2274：252-262.

[6]BOER B D，LEMKE K，WICKE G.A DPA attack against the modular reduction within a CRT implementation of RSA[C].International Workshop on Cryptographic Hardware and Embedded Systems，CHES 2002，LNCS，2003，2523：228-243.

[7]YEN S M，LIEN W C，MOON S J，et al.Power analysis by exploiting chosen message and internal collisions-vulnerability of checking mechanism for RSA-decryption[J].Proceedings of Progress in Cryptology，Mycrypt 2005，2005，3715：183-195.

[8]Chen Tingding，Li Huiyun，Wu Keke，et al.Countermeasure of ECC against side-channel attacks：balanced point addition and point doubling operation procedure[C].Asia-Pacific Conference on Information Processing,APCIP 2009，2009，2：465-469.

[9]KIHARA S.On the rank of elliptic curves with a rational point of order 4[J].Proceedings of the Japan Academy，Series A，Mathematical Sciences，2004，80(4)：21-34.

[10]KIHARA S.On the rank of elliptic curves with three rational points of order 2.Ⅲ[J].Proceedings of the Japan Academy，Series A，Mathematical Sciences，2004，80(3)：13-20.

[11]KIHARA S.On the rank of elliptic curves with a rational point of order 4.Ⅱ[J].Proceedings of the Japan Academy，Series A，Mathematical Sciences，2004，80(8)：151-168.

[12]Li Huiyun，Wu Keke，Xu Guoqing，et al.Simple power analysis attacks using chosen message against ECC hardware implementations[C].World Congress on Internet Security，2011：68-72.