基于Krawtchouk-RBF的印章图像分类识别*

余 彪 ，万水龙，刘 进 ,王强德

(1.中国人民解放军92493部队,辽宁 葫芦岛 125000;2.中国人民解放军91960部队,广东 汕头 515074;3.南京航空航天大学,江苏 南京 210016)

分类识别是印章图像处理的最终目的，分类的准确与否、识别率的高低是其中的重要评判标准[1]。只有提取到印章图像的关键特征，才有可能改进分类的准确度，而识别率的提高就要求选择一款性能良好的分类器。矩函数对图像形状能进行有效的描述,因而得到迅速发展，如Tchebichef矩、Krawtchouk矩、Zemike矩和Legendre矩[2]，其中Krawtchouk矩是基于离散域的正交矩，不存在数字过程中的近似误差和计算中的坐标变换问题。参考文献[3]将Krawtchouk矩用于对运动目标进行分类，有效地提高了分类的准确率。与此同时，人工神经网络ANN(Artificial Neural Network)自提出以来就得到了快速发展，其中径向基函数RBF(Radial Basis Function)神经网络具有良好的非线性映射、自学习能力和收敛性，因此被越来越多地运用于对目标的分类当中，取得了较好的分类效果[4-6]。

基于此，本文提出一种基于Krawtchouk矩和RBF神经网络的印章图像分类识别方法。首先提取出标准印章图像的Krawtchouk矩不变量，将其作为RBF神经网络的原始训练样本;然后提取全部待鉴印章图像的Krawtchouk矩不变量，将其作为RBF神经网络的输入量进行分类识别。实验表明,使用Krawtchouk矩来描述印章图像的特征并通过RBF神经网络来对其进行分类识别,相对于参考文献[4]中的KPCA-RBF法和参考文献[6]中的Brushlet-RBF法,其分类更准确,识别率更高。

1 Krawtchouk矩不变量

Krawtchouk矩是以Krawtchouk多项式为基础的一种正交矩。一般来说，n阶Krawtchouk多项式定义为：

其中，x，n=0,1,…,N;N＞0;p∈(0,1);2F1(a,b;c;z)是超函数。

其中，Krawtchouk多项式的加权表达式为：

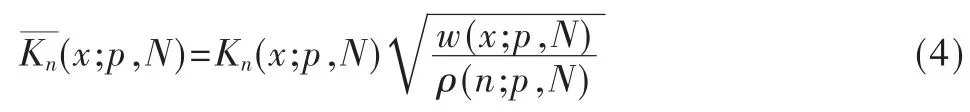
其中，

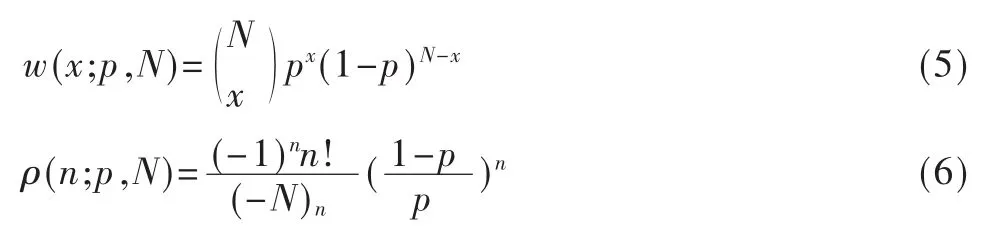
现用 Krawtchouk矩来描述一幅大小为M×N的图像f(x,y)：

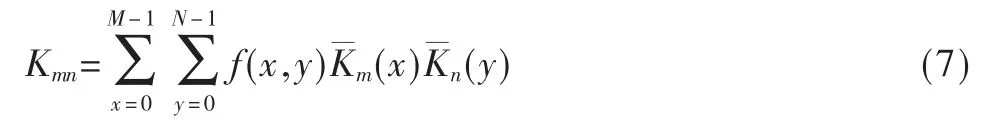
其中，

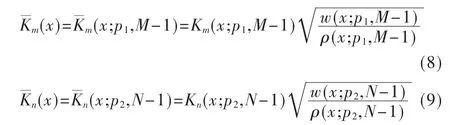
Krawtchouk矩不变量具有平移、旋转、尺度不变性，可表示为：

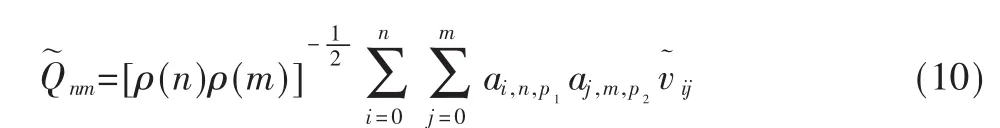
其中，

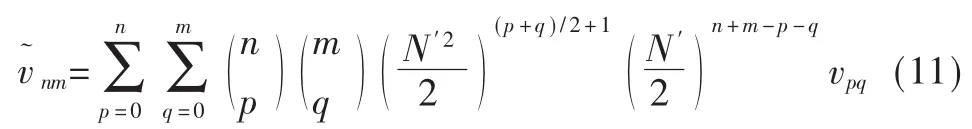
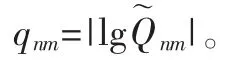
利 用q01、q10、q11、q02、q20、q12、q217 个 不 变 量 构 造 一 个不变向量Q来描述一幅图像，其中q01、q10与图像内容无关，所以本文选择其余5个变量：

通过式(12)构成的特征向量对印章图像进行特征提取。

2 RBF神经网络及其改进算法

2.1 RBF神经网络

RBF神经网络由输入端、隐藏段和输出端3部分组成，具体的结构如图1所示。输入端将输入信号传输到隐藏段，隐藏段再通过基函数的响应激烈程度给予输出端相应的输出信号。其中，输入端的节点数对应于输入向量的维数，隐藏段的节点数要视实际情况而定，输出端的节点数按分类的类别总数来确定。

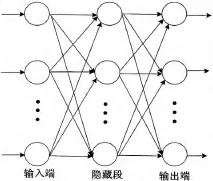
图1 RBF神经网络结构

一般来说，径向基函数选取高斯函数，其具体形式为：

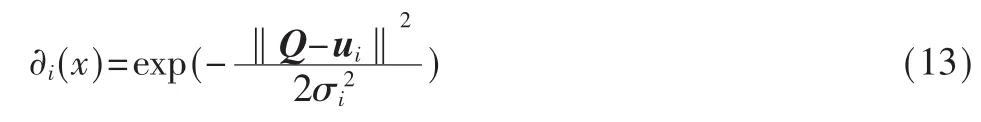
其中，Q为输入向量，ui为隐藏节点i的中心向量，σi为相应的宽度，‖Q-ui‖为欧式范数。

输出端第j个节点的输出值yi为：

其中，j=1,…,m为输出端节点，wij为隐藏段第i个节点到输出端第j个节点的连接权值。

令d为训练样本的期望输出值，则可知：

2.2 改进算法

RBF神经网络的学习过程一般分为选取中心、确定宽度和导出连接权值3部分。选取中心的方法通常采用K-means 聚类、ROLS(Recumive Orthogonal Least Square)法和自组织聚类等，然后根据标准样本来确定宽度，最后通过误差导出隐藏段各节点到输出端各节点的连接权值。

本文算法的具体描述如下：

(1)根据印章图像的特点，对于第一个输入向量Q1=(q11,q02,q20,q12,q21)来说，此时RBF网络的隐藏段只有一个节点，中心为Q1。现设定一个参数a(该参数会根据实验结果进行适当调整)，对于第二个输入向量Q2，计算其与Q1之间的欧氏距离D，若D＞a，则 Q2也成为一个中心；若D≤a，则 Q1为此处的中心。对于第n个输入向量Qn，此时已有M个中心，现分别计算Qn与这M个中心的欧式距离，其中D0为其中的最小值，若D0＞a，则 Qn成为新一个中心；若D0≤a，则中心数仍为M个。

(2)因为本文选取的径向基函数为高斯函数，所以可通过式(16)直接求取宽度：

(3)隐藏段至输出端的连接权值可直接用ROLS法求得：

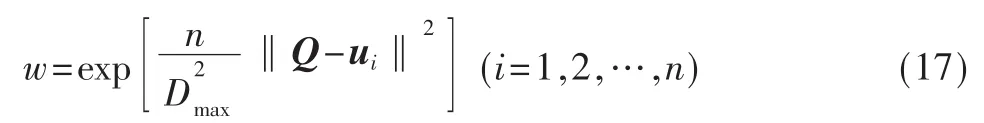
3 算法实现

算法实现的具体过程如下。

(1)提取标准印章图像的Krawtchouk矩不变量，将其作为RBF神经网络的原始训练样本。

(2)提取全部待鉴印章图像的Krawtchouk矩不变量，通过RBF神经网络对其进行分类。

(3)分类结果分为正确、错误和可疑3类，并在实验中分别用阿拉伯数字1、-1和0表示。

具体的流程图如图2所示。

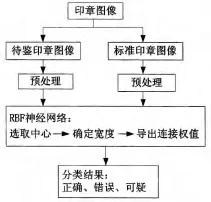
图2 RBF神经网络分类流程图

4 实验结果及分析

为了验证本文提出的基于Krawtchouk矩和RBF的印章图像分类识别方法的分类识别情况，针对大量不同类型的印章图像做了实验,并与参考文献[4]中的KPCA-RBF法和参考文献[6]中的Brushlet-RBF法进行了比较，发现本文方法优势明显。实验是在Intel(R)Core(TM)i3 CPU 2.4 GHz/1.92 GB内存/Matlab 2009a环境中运行的。

图3 印章图像实验用图

表2 RBF神经网络分类识别结果

印章图像(323×324)在5种不同条件下所盖印出来的效果如图3所示。先进行去噪、分割及配准等预处理，然后通过Krawtchouk矩不变量提取图像特征，结果数据如表1所示。再利用RBF神经网络来进行训练，RBF神经网络结构中输入端节点数选为5，输出端节点数选为3，最后再将所有待鉴印章图像通过该网络来分类识别，结果数据如表 2所示,其中 1代表正确，0代表可疑，-1代表错误。

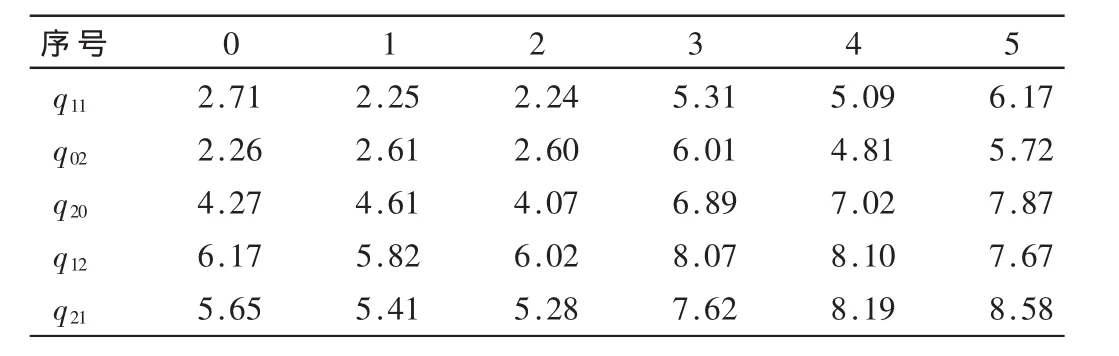
表1 印章图像的特征向量参数

图4所示印章图像中后3幅图像对原图中的字体、形状或面积进行了一定的变动，并将得到的印章通过用力过大、用力过小、用力不均、缺上角、缺下角等方式产生实验用的全部待鉴印章图像，按照先后顺序编号为1～5,6～10,11～15,16～20，然后将其输入 RBF 神经网络来对其进行分类识别，结果如表3所示。

图4 待鉴印章图像

表3 各类方法效率比较

从表2可以看出,本文方法、KPCA-RBF法和Brushlet-RBF法对于原始印章图像及变换了图像形状的分类均取得了较好的结果，但是对于只改变了字体或字体间间距的图像来说，本文方法具有明显的优势。由表3可以看出,本文提出的Krawtchouk-RBF法相对于KPCA-RBF法和Brushlet-RBF法来说，其分类识别的正确率更高。

本文提出了一种基于Krawtchouk矩和RBF神经网络的印章图像分类识别方法。首先提取标准印章图像的Krawtchouk矩不变量，将其作为RBF网络的原始训练样本；然后提取全部待鉴印章图像的Krawtchouk矩不变量，将其作为RBF神经网络的输入量进行分类识别。针对实际印章图像做了大量的实验,并与参考文献[4]中的KPCA-RBF法和参考文献[6]中的Brushlet-RBF法进行了对比，结果表明，本文的方法分类更准确，识别率更高。

[1]何瑾,刘铁根,周怡洁,等.基于边缘差异的印鉴自动鉴别[J].仪 器 仪 表 学 报 ,2010,31(1)：85-91.

[2]CHONG C W,RAVEENDRAN P,MUKUNDAN R.Translation and scale invariants of Legendre moments[J].Pattern Recongniton,2004(37)：119-129.

[3]王晓静,原达,李道凯.基于krawtchouk矩的运动目标分类[J].计算机工程与设计,2012,33(5)：1890-1894.

[4]杨俊,陈贤富.基于KPCA和RBF网络的文本分类研究[J].微电子学与计算机,2010,27(3)：122-125.

[5]王行甫,覃启贤,程用远,等.一种改进的径向基神经网络预测算法[J].计算机系统应用,2012,21(8)：214-217.

[6]李晓辉,谢建红,高鑫.基于 Brushlet和 RBF网络的SAR图像分类[J].微计算机信息,2009,25(2-3)：295-297.