地下铁道盾构施工测量检测方法探讨

廖振宇

(佛山市铁路投资建设集团有限公司， 广东佛山 528000)

地下铁道盾构施工测量检测方法探讨

廖振宇

(佛山市铁路投资建设集团有限公司， 广东佛山 528000)

结合广佛城际轨道交通[菊树—西塱]盾构区间施工测量检测的实践，介绍两井定向、陀螺定向和盾构环姿态测量在地铁盾构法施工测量检测中的应用。

地下铁道 测量检测 两井定向 陀螺定向 盾构环姿态

1 工程概况

珠江三角洲城际快速轨道交通工程广佛线[菊树—西塱]盾构施工区间， 左线设计里程ZDK18+424.368～ZDK20+340.068，全长1908.007 m， 短链7.693 m；右线设计里程YDK18+423.206～YDK20+339.345，全长1916.139 m。隧道埋深：-7.789m～-16.947 m。 沿线经过珠江水产研究所、花地湾河和广州地铁一号线，其余部分区域较为空旷，建筑物较少。

本区间所处地形较平坦，地貌属于海相冲积平原地貌特征，地质构造相对较为简单。基岩岩性主要为紫红色泥质粉砂岩、泥岩组成，夹含砾粉、细砂岩、砾岩；地下水类型主要有两种：一种为赋存于第四系土层中的孔隙水；另一种是赋存于基岩风化层及构造破碎带中的裂隙水。本区间适宜盾构掘进，隧道全线采用土压平衡盾构法施工，隧道开挖面直径6.0 m，环片长度1.5 m。

2 地面控制测量

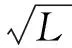
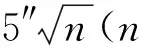
3 施工测量检测

3.1 两井定向联系测量

(1)平面联系测量

两井定向时，利用地面趋近导线测定两吊锤线的平面坐标值。在隧道中，将已布设的地下导线与竖井中的吊锤线连测，即可将地面坐标系中的坐标与方位传递到井下，经计算求得井下导线各点的坐标与导线边的方位。

两井定向外业工作包括：投点、地面与地下连接测量(如图1所示)。

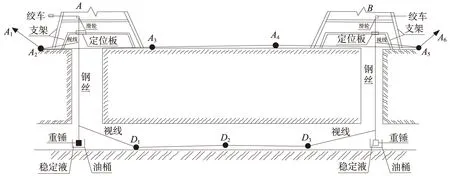
图1 两井定向联系测量示意

两井定向的内业计算工作：

①根据地面连接测量的成果，按照导线的计算方法，计算出地面两钢丝A、B的平面坐标(xA，yA)、(xB，yB)。

②计算两钢丝点A、B的连线在地面坐标系统中的方位角αAB

(1)

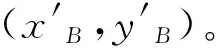
④计算A、B连线在假定坐标系中的方位角

(2)

⑤计算井下起始边在地面坐标系统中的方位角αAI

(3)

⑥根据A点的坐标(xA，yA)和计算出的A1边方位角αAI，计算出井下导线各点在地面坐标系统中的坐标方位。

平面联系测量外业注意事项：

①两钢丝间距离应大于30 m，且越长越好，减少投点误差。

②宜采用φ0.3～φ0.5 mm直径高强度钢丝，悬挂10 kg重锤，并浸没在阻尼液中。

③定向均应独立进行3次，取3次的平均值作为定向成果。

④如果左右线同时做两井定向且4根钢丝能互相同视，可动两次钢丝，相互连测，得出4组基线，取其平均值作为盾构始发的基线。

(2)高程传递测量

通过竖井高程传递，将近井水准点的高程，传递到井下高程测量起始点上。近井点的设置主要考虑点位稳固和传递高程方便两个因素。采用Ⅱ等水准测量技术，通过精密水准点引测至近井水准点，水准路线进行往、返观测。

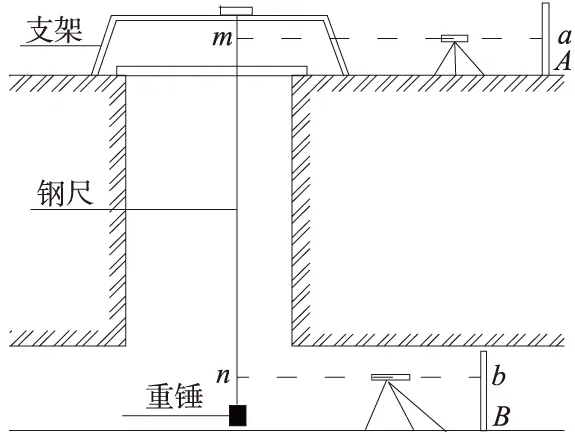
图2 钢尺导入法传递高程

在地面搭建一悬挂钢尺尺架，将鉴定过的钢尺悬挂其上，下放到井下(如图2所示)，A为地面水准点，B为地下水准点，将钢尺悬挂于井上，使其自然下垂，钢尺零点位于井下。在地面和井下分别安置水准仪，在A、B所立水准尺上取读数a、b，然后在钢尺上同时读取读数m、n，此外还需测定井上井下温度t上、t下。

为防止出现粗差和提高观测精度，仪器高变动3次、钢尺变动两次进行观测，测定井上、井下水准点高差的不符值(高差的不符值<±3 mm)。最终取3次观测成果的平均值，从而得到高精度井下水准点高程。根据下面公式可求得B点高程

(4)

式中，∑Δl为钢尺改正数的总和，包括

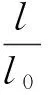
温度改正：Δlt=αl(t-t0)，α钢尺的膨胀系数。

其中温度改正用井上井下实测温度的平均值， 式中，γ为钢的单位体积重量，为7.8 g/cm3；E为钢尺的弹性模量，一般取2×106kg/cm2，L为钢尺悬挂点至地下挂锤球处的自由悬挂长度；l为井上、井下水准仪视线间的钢尺长度，即l=m-n。

3.2 陀螺经纬仪定向

陀螺经纬仪是陀螺仪和经纬仪组合而成的定向仪器。运用陀螺经纬仪进行隧道方位定向的常用方法主要有逆转点法和中天法。下面以逆转点法为例来说明测定井下未知边方位角的全过程。

在地面已知方位边上采用2～4个测回测定仪器常数△前。

由于仪器本身条件和外部环境的影响，实际陀螺轴的平衡位置与测站真子午线的方位不重合，其夹角为陀螺经纬仪的仪器常数，用△表示。△需要在地面已知方位边上测定，关键是要测定已知边的陀螺方位角TAB陀。测量TAB陀的步骤如下：

①在任意一点安置陀螺经纬仪，严格对中整平，以盘左盘右两个观测值的均值作为已知方位边的测前方位值M1。

②将经纬仪的视准轴对准北方向，使其偏离陀螺子午线方向不大于60′。

③测量悬挂带零位值(测前零位)，同时用秒表测定陀螺摆动周期。

④启动陀螺马达，缓慢下放灵敏部，使摆幅在1°～3°范围内。调节水平微动螺旋使光标像与分划板零刻度线随时保持重合，达到逆转点后，记下经纬仪水平度盘读数。连续记录5个逆转点的读数，计算NT。

⑤进行测后零位观测。

⑥以盘左盘右两个方向值测定已知边的测后方位值M2。

⑦计算TAB陀。

于是可得

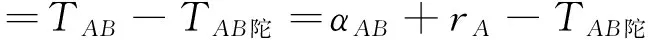
(5)

在井下定向边上采用对向观测、四测回测定陀螺方位角TAB陀。

返回地面后，及时在已知方位边上测定仪器常数△后。

计算井下测边的坐标方位角αab

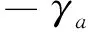
(6)

式中,γa为α点的子午线收敛角。

3.3 盾构机环片姿态检测

地铁隧道工程施工过程中，为了及时检测环片拼装的横向偏差和竖向偏差，确保隧道按设计要求准确贯通，在隧道掘进过程中，每隔一段时间用人工测量的方法对盾尾稳定的环片进行检校，以检核盾构机姿态的正确性。

根据成型隧道内径制作一铝合金标尺，在铝合金标尺正中央位置做标识，并在其侧面贴上反射片，上部粘贴水平尺。测量时，将铝合金标尺水平放置在某一环片上，首先用水平尺把铝合金标尺精确整平，使用全站仪采用极坐标法测量铝合金标尺的中心坐标(X测，Y测，Z测)，此时测出的Z测并不是环片中心的真实坐标，需要根据环片的半径和铝合金标尺的长度计算真实的Z实坐标

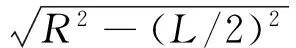
式中，R为环片半径，L为铝合金标尺长度。

使用计算机计算管片姿态时，将全站仪采集的外业数据，通过专业软件传输下载并复制到EXCEL表格中，编辑成CAD可识别的三维坐标，然后通过展点程序将整理好的三维坐标在隧道设计线路图上画出来，展点时一定要关闭对象捕捉命令。点位画出来后，就可以通过CAD中的查询命令直接测量管片的水平和垂直姿态。通过此种测量和计算方法，大大提高了环片检测的准确度。

4 数据处理与精度分析

4.1 竖井附近趋近导线测量

测量过程中，受仪器本身、外部环境和测量人员操作影响，不可避免地会产生测量误差，因而需对每次联系测量的成果进行分析，以确保地铁隧道施工的高精度性。以[菊树-西塱]盾构区间为例，精密导线控制点GF076、GFJ077、GFJ078、GFJ079形成附合导线；内业经严密平差后， 最大点位中误差为±2.5 mm，最大点间中误差为±1.8 mm，导线全长相对中误差为1/106 544，均满足精密导线作业精度要求，为后续的联系测量提供了高精度的数据基础。

4.2 两井联系测量

当车站或区间竖井具备两井定向条件时，应采用两井定向方法。菊树站长约200 m左右，且车站两端都留有盾构施工用的吊出井，因此在车站两端左右线四个井口各投测一个坐标点，井上井下将投点用导线连接，构成两井定向图形。施工期间在菊树站前后进行了五次两井定向联系测量。基线方位成果见表1。其中左线基线边长为80.960 4 m，方位角平均值为92°20＇29.96″，最大互差为5.3″；右线基线边长75.197 6 m，方位角平均值为92°25＇50.37″，最大互差为5.47″；高程最大标准偏差2.3 mm，最大互差为3.7 mm。

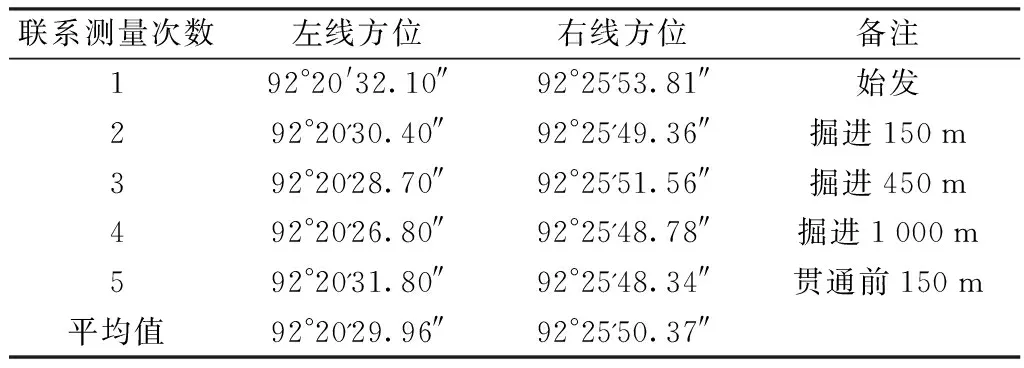
表1 联系测量基线边方位角

4.3 陀螺经纬仪定向

本工程采用的陀螺经纬仪是AGT-1高精度自动陀螺经纬仪，该陀螺经纬仪一次定向标准偏差小于5"，自动寻北时间8 min，一测回需20 min。该仪器整个系统在掌上电脑的控制下，按中文菜单的指引，完成所有已知数据的输入，测前测后自动零位测量，自动寻北、自动检核，测量误差计算与数据处理，全部测量过程和测量结果自动存储、显示。

在隧道掘进至1 200 m时左、右线各进行了一次陀螺定向。对比支导线测量的导线边方位和陀螺经纬仪定向的方位(见表2)可以看出，地下支导线的精度满足盾构掘进要求。

表2 陀螺与导线测量方位角对比

4.4 盾构环片姿态测量

在盾构掘进至150 m、450 m、1000 m和贯通前150 m，分别对盾构机环片姿态进行了检测，通过数据处理和统计，发现最大横向偏差为-49 mm，最大纵向偏差为-35 mm。均满足规范要求。由图3和图4可以看出，环片姿态误差的分布规律均在限差±50 mm以内，且均匀分布在0值附近。

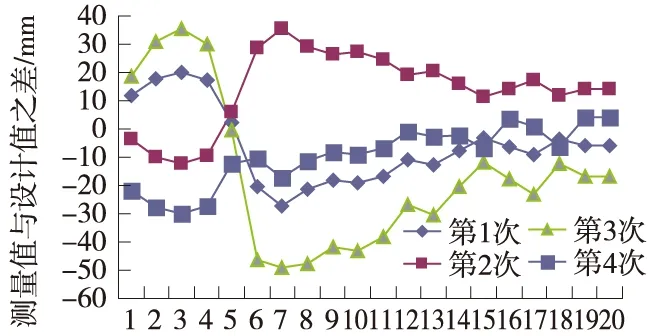
图3 盾构线路中心坐标实测值与设计值之差(横向)

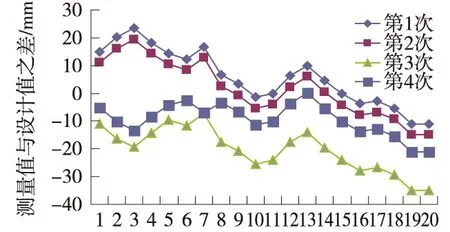
图4 盾构线路中心坐标实测值与设计值之差(纵向)

在西塱站贯通后测得贯通平面误差为：左线横向贯通误差为38.5 mm，纵向贯通误差为1.0 mm，高程贯通误差为1.9 mm；右线横向贯通误差为30.0 mm，纵向贯通误差为28.6 mm，高程贯通误差为6.4 mm，满足规范和设计要求。

5 结束语

综上所述，珠江三角洲城际快速轨道交通广佛线[菊树—西塱]盾构区间隧道施工测量检测成果均满足《城市轨道交通工程测量规范》(GB50308—2008)的要求，为该区间隧道的顺利贯通提供了保障，为后续铺轨和机电安装工程的顺利实施奠定了坚实的基础。广佛线是国内首条城际快速轨道交通项目，广佛线的顺利贯通为城际轨道交通的施工测量检测积累了丰富的经验，为日后城市轨道交通工程隧道施工测量乃至城际地下隧道测量检测奠定了理论与实践基础。

[1] 秦长利，马全明，等.城市轨道交通工程测量规范[M]北京:中国建筑工业出版社，2008

[2] 于来法.陀螺定向[M].北京：解放军出版社，1998

[3] 秦长利.城市轨道交通工程测量[M].北京:中国建筑工业出版社，2008

[4] 李青岳，陈永奇.工程测量学[M].北京:测绘出版社，2008

[5] 冯冬健，潘庆林，张凤梅.地铁盾构施工中盾构机姿态定位测量的研究[J].工程勘察，2003(5)

[6] 王超领，张永超.地铁盾构机掘进实时姿态定向测量的研究[J].隧道建设，2007，6(27)

[7] 潘国荣，黄加惠.地铁隧道盾构掘进的定向与贯通[J]，铁路航测，1997(2)

[8] 毕小伟.盾构机位姿测量系统的关键技术研究[D].上海：上海交通大学，2010

[9] 王暖堂.盾构隧道施工中的测量技术研究[J].铁道建筑，2002(12):1-5

[10]潘国荣，王穗辉.地铁盾构施工中的若干测量手段及方法[J].测绘通报，2001(1):23-25

[11]吕宏权.浅析地铁盾构隧道的施工测量[J].隧道建设，2005，25(5):65-67，75

[12]汪玉勤.长区间盾构施工地铁隧道的测量控制方法[J].铁道勘察，2007(2):1-3，7

[13]徐浩，杨卓.盾构竖井联系测量的几种方法探讨[J].山西建筑，2009，35(6):353-354

[14]李国华.盾构机姿态控制点测量模型及其应用[J].隧道建设，2006，26(SO):19-22

[15]任福松，金建俊.地铁施工中的盾构机姿态控制研究[J].交通标准化，2009(9):134-137

[16]徐浩，杨卓.地铁盾构施工中人工测量盾构机姿态的方法[J].山西建筑，2009，35(4):355-357

[17]秦长利.提高盾构施工测量精度的要点及方法[J].北京测绘，2003(3):1-3

ExploretheUndergroundRailroadShieldConstructionMeasurementDetectionMethod

LIAO Zhen-yu

2014-04-30

廖振宇(1979—)，男，2003年毕业于中国地质大学(武汉)岩土工程专业，工程师。

1672-7479(2014)04-0016-04

TB22

： B