安装偏心距对球式自动平衡装置减振的影响

李镔桦，谭青，蔡小华，任志湘

(中南大学机电工程学院，长沙410083)

安装偏心距对球式自动平衡装置减振的影响

李镔桦，谭青，蔡小华，任志湘

(中南大学机电工程学院，长沙410083)

过临界转速下，影响球式自动平衡装置减振效果的因素很多。通过建立存在安装偏心距的球式自动平衡装置的数学模型，并依据现有的实验台确定仿真参数进行数值仿真，分析安装偏心距对球式自动平衡装置减振效果的影响。结果表明，安装偏心距越小，球式自动平衡装置的减振效果越好；一定范围内，提高转子的加工精度和安装精度，减小安装偏心距，球式自动平衡装置的减振效果改善明显；但过高的提高转子的加工精度和安装精度，球式自动平衡装置的减振效果改善不明显。分析结果对于球式自动平衡装置的有效减振有一定的应用价值。

振动与波；安装偏心距；球式自动平衡装置；数学模型；数值仿真；减振

对于回转机械而言，转子不平衡将导致回转机械产生振动和噪声，甚至会引发灾难性破坏，由此造成的损失不容忽视。目前，解决这一问题的一般方法是对其回转部分（即转子）进行高精度的动静平衡[1]。但对于转子质量可能发生改变的回转机械，如粉尘环境中的风机，尘粒和水份附着于风机的叶片上便引起转子质量分布改变，经常对其进行动静平衡是很不方便的。由此，学术界展开了自动平衡课题的研究。自动平衡装置分为两大类：一类是自动定心型自动平衡装置[2]；另一类是微机控制型自动平衡装置[3,4]。

自动定心型自动平衡装置的工作原理是：转子在过临界转速下旋转时，转子内可移动质量的位置将自动的受转子机械振动相位的影响，移动到偏心质量的另一边，一定程度上抵消偏心质量所产的离心惯性力，从而起到减振的作用[2]。以往的研究中，通常认为自动平衡装置的安装是理想的（零偏差）。然而实际生产中，由于转子旋转轴的塑性变形或者加工、安装精度的影响，可能导致安装后的自动平衡装置的旋转中心线与回转机械的旋转中心线不重合，即存在安装偏心距。本文主要研究安装偏心距对球式自动平衡装置减振效果的影响。

1 建立数学模型

球式自动平衡装置与待平衡的回转机械装配时经常会出现如图1所示的情况。

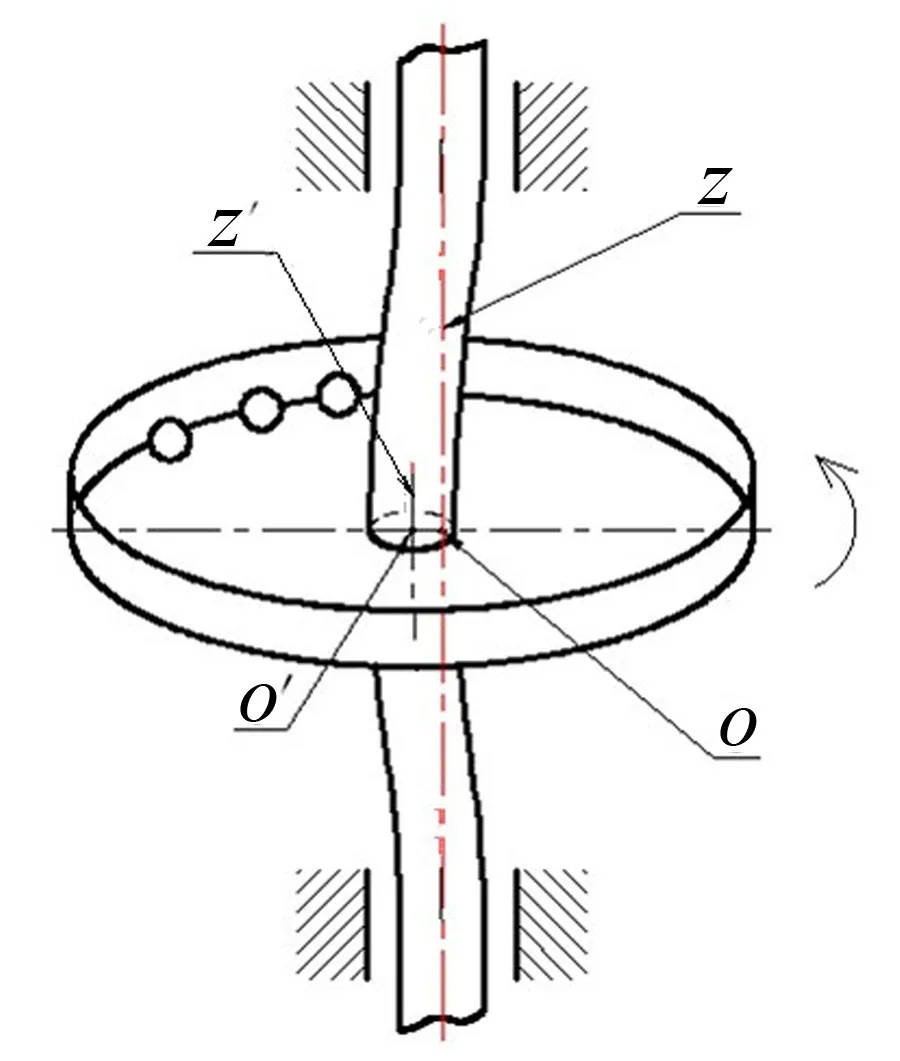
图1 球式自动平衡装置的安装示意图

如图1所示，对于旋转轴较长回转机械的旋转轴部分轴段常会出现塑性变形，理想旋转轴线为z，实际旋转轴线为z'。O'点为轴线z'与滚球式自动平衡装置转盘面的交点，O点为轴线z与转盘面的交点，O与O'不重合，O与O'间的距离即为安装偏心距。

现将球式自动平衡装置的结构简化为转盘和滚球两部分，并做如下假定：（1）转盘为均质圆形薄盘；（2）电机驱动力矩足够大，转速不因阻力矩大小而变化；（3）滚球运动为纯滚动；（4）转盘及滚球的粘性阻力和速度成正比；（5）不考虑轴向运动和重力作用。

球式自动平衡装置常用于单盘转子的减振，其力学模型如图2所示。

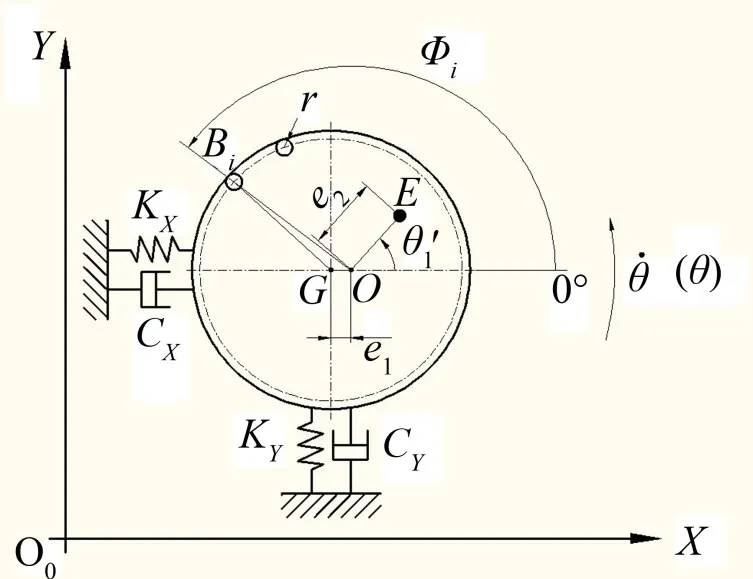
图2 存在安装偏心距的球式自动平衡装置的力学模型

本文所采用的符号如下：

O0XY：平面直角定坐标系；

O0：坐标原点，即系统静止时图1中z轴与转盘面的交点；

O：图1中z轴与转盘面的交点，静止时与O0重合；

O′：图1中z'轴与转盘面的交点；

G：转盘的质心，因为假定（1），所以G与O’是重合的；

E：偏心量的位置点；

Bi：第i个球的质心（i=1，2，3...）；

e1：点G与点O的距离（即安装偏心距），单位m；

e2：点E与点O的距离，单位m；

X,Y：O点的坐标；

CX,CY：系统X方向上的粘性阻力系数和Y方向上的粘性阻力系数，单位N·s/m；

Kx,KY：系统X方向上的刚度和Y方向上

的刚度，单位N/m；

n：滚球个数；

m1，m2，m3，m：转盘的质量，偏心量的质量，电动机质量，单个滚球质量，单位kg；

M：系统的总质量，

单位kg，M=m1+m2+m3+nm；

r，R：滚球的半径和公转半径，单位m；

I：滚球对其质心的转动惯量，单位Kg·m2；

θ：转盘的转角即电动机主轴转角，逆时针为正，单位rad；

ω：转盘的角速度，ω=θ˙，单位rad/s；

θ1：偏心质量的初始转角，单位rad；

φi：第i个滚球的转角（公转）（i=1，2，3...），单位rad；

β0：滚球的滚动摩擦因数，单位m（长度纲量）；

β1：滚球粘性阻尼系数，单位N·s/(m·rad)；

FL，FM：系统的粘性阻尼力和滚动摩擦力。

如图2所示，系统的运动限定在X O0Y平面内。系统的数学模型可利用拉格朗日方程[5]来描述

其中T表示系统的总动能，包括转盘的动能T1、偏心量的动能T2、滚球的动能T3和电动机的动能T4；V表示系统的总势能；qα表示系统的广义坐标；Qα表示系统的广义力；s表示广义坐标个数。

系统的运动是限定在X O0Y平面内的，属于平面运动。要描述整个系统的位置，需确定转盘、偏心量和滚球的位置，而转盘和偏心量的相对位置是固定的，所以只需确定转盘和滚球的位置。转盘的转角即为电动机主轴的转角，即θ是已知的，则广义坐标个数s=n+2，因此系统的广义坐标可表示为

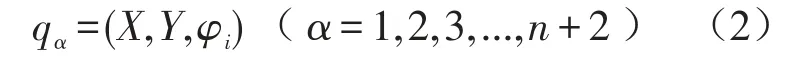
考虑到转盘和偏心量是相对静止的，故可将二者视为一个整体，用T12表示该整体动能；G12表示该整体的质心；I12表示该整体对其质心G12的转动惯量。

转动中心O、转盘质心G、偏心量E、滚球质心Bi及转盘和偏心量的合成整体的质心G12的位置矢量可表示为

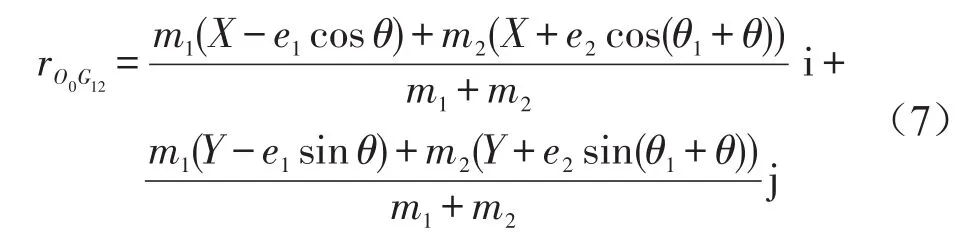
其中，i，j分别为X轴和Y轴正方向上的单位矢量。

系统的总动能T

系统的总势能

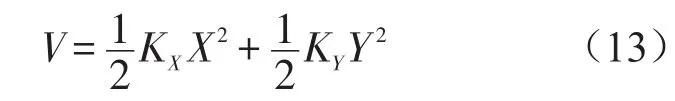
系统的广义力Qα可以由式（14）求出

由此，推出系统的控制方程如下：

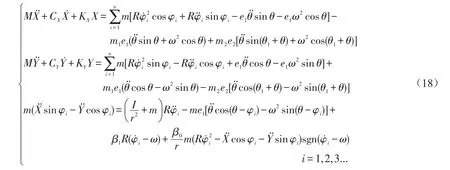
2 系统的数值仿真

2.1 数值计算方法

机械系统的数学模型一般都是微分方程或微分方程组，数值积分法是对其进行数值解析的重要方法之一，主要包括欧拉法、梯形法、龙格—库塔法及亚当姆斯法，其中四阶龙格—库塔法是最为常用的数值计算方法。

2.2 模型的降阶和仿真程序流程图

以两滚球为例（n=2），对系统进行降阶处理。设

降阶后，系统1阶微分方程组如下

基于4阶龙格—库塔法编写仿真程序，流程图如图3所示。

2.3 数值仿真结果

实验台X方向的粘性阻尼系数与Y方向的粘性阻尼系数相等，即CX=CY=C；X方向的刚度与Y方向的刚度相等，即KX=KY=K；根据实验台的参数确定仿真参数，如表1所示。

由上述8组仿真仿真结果可知，安装偏心距e1取不同值时，系统进入稳态的时间基本相同，但随着安装偏心距e1的增加，系统稳态时的振幅也在相应的增大。当e1＜200μm时，装有球式自动平衡装置的系统稳态振幅小于无自动平衡装置的系统稳态振幅；当e1=200μm时，装有球式自动平衡装置的系统稳态振幅（0.202 4 mm）与无自动平衡装置的系统稳态振幅（0.213 8 mm）接近；当e1＞200μm时，装有球式自动平衡装置的系统稳态振幅大于无自动平衡装置的系统稳态振幅。

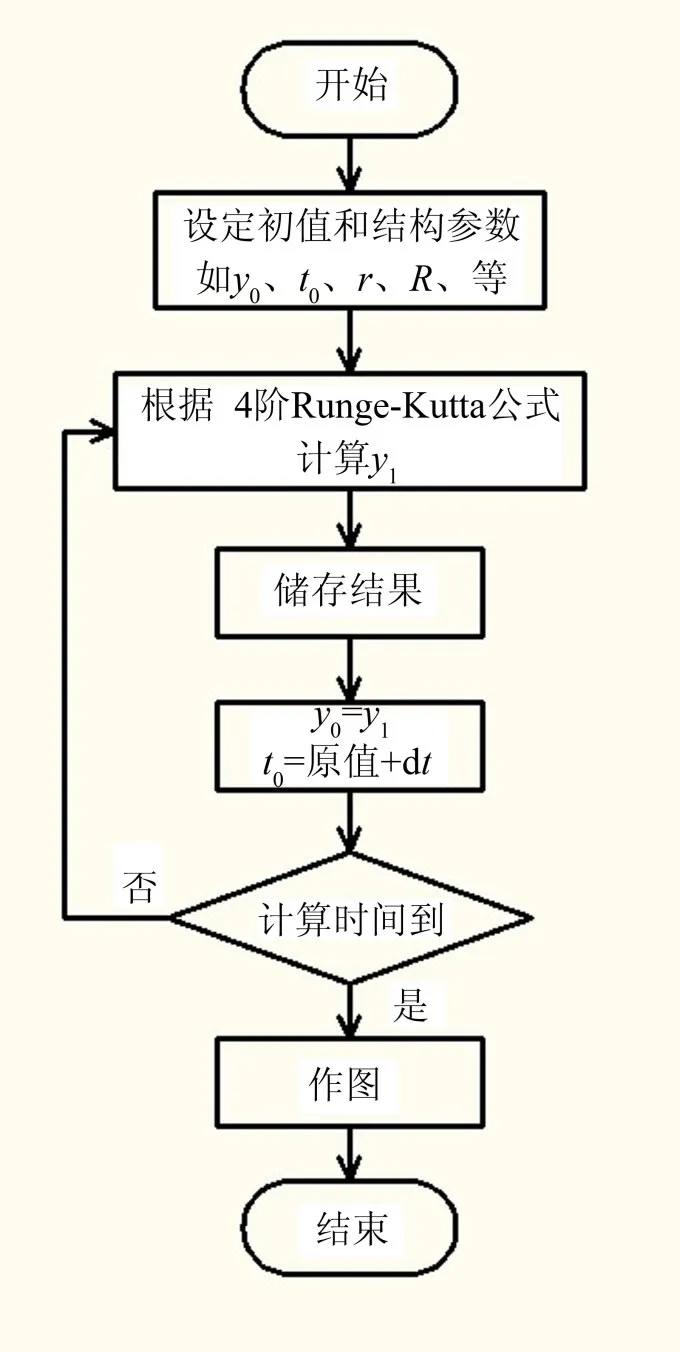
图3 仿真程序流程图

表1 仿真参数

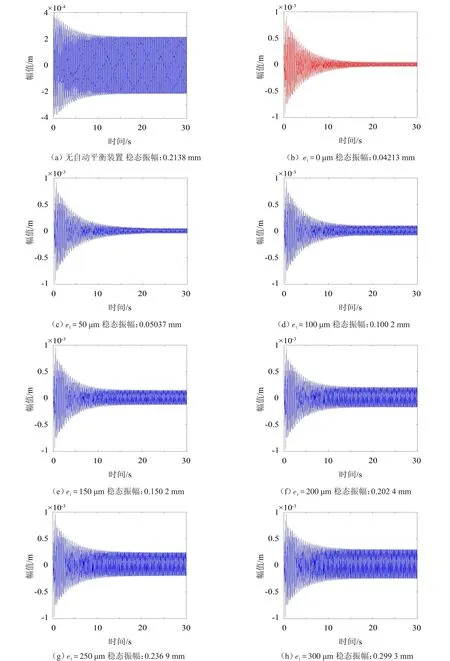
图4 不同安装偏心距下，系统X方向的振动图像

根据以上仿真数据绘制球式自动平衡装置的减振倍数[6]曲线，如图5所示。

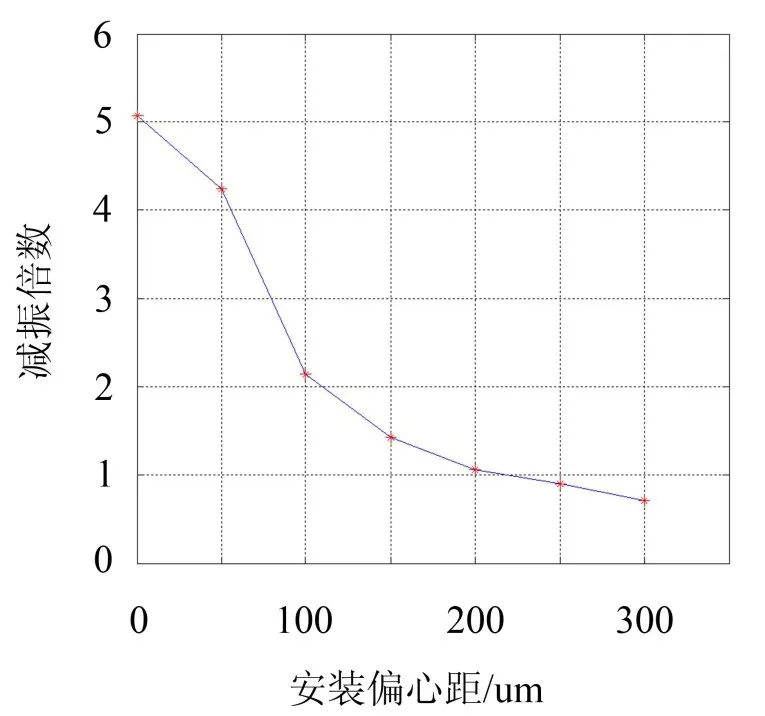
图5 减振倍数曲线

本文中减振前系统稳态振幅即无自动平衡装置的系统稳态振幅，减振后系统稳态振幅即装有球式自动平衡装置的系统稳态振幅。减振倍数大于1，说明球式自动平衡装置对系统具有减振作用，且减振倍数越大，减振效果越明显；减振倍数等于1，说明球式自动平衡装置对系统无作用，反而增加了系统的负担；减振倍数小于1，说明自动平衡装置对系统起增振作用，加剧系统的振动，具有危险性。

如图5所示，可得如下结论：

1)当e1＜200μm，减振倍数大于1，球式自动平衡装置对系统具有减振作用，随着安装偏心距的减小，减振效果越好；

(1)e1=0～50μm时，减振效果最好，在此范围内改变e1取值，减振倍数大小变化较慢；

(2)e1=50～100μm时，减振效果好，在此范围内改变e1取值，减振倍数大小变化快；

(3)e1=100～200μm时，减振效果一般，在此范围内改变e1取值，减振倍数大小变化缓慢；

2)当e1=200μm，减振倍数约等于1，球式自动平衡装置对系统减振作用不明显，可以认为无减振作用；

3)当e1＞200μm，减振倍数小于1，球式自动平衡装置对系统不具有减振作用，相反起到增振作用。

3 结语

对于球式自动平衡装置，安装偏心距的大小将会影响其减振效果，安装偏心距大可能起不到减振作用，甚至出现增振的现象。对于需要安装球式自动平衡装置的回转机械而言，一定范围内提高待安装部分的加工精度和安装精度，减振效果将会得到明显改善；但过高的提高加工和安装精度，对减振效果的影响也不是很明显，而且还会增加安装费用。

[1]刘文倩，谭青，谢燕琴，聂卫东.自动平衡装置减振效益分析[J].噪声与振动控制，2010，30(4)：153-157.

[2]谭青，周铁，黄秀祥.球式自动平衡装置的数值仿真与实验研究[J].噪声与振动控制，2008，28(3)：142-145.

[3]陶利民，葛哲学，温熙森.刚性转子自动平衡控制策略[J].机械科学与技术，2004，23（2）：140-142.

[4]曾胜，汪希萱.电磁式在线自动平衡调节器的原理及其实验[J].流体机械，1997，25（5）：11-14.

[5]叶敏，肖龙翔.分析力学[M].天津：天津大学出版社，2001，140：145.

[6]王立杰，谭青.摆锤式自动平衡装置的建模与仿真[J].噪声与振动控制，2012，32(2)：34-36.

Influence of Installation Eccentricity on Vibration Reduction Effect of Ball-type Automatic Balancers

LI Bin-hua,TAN Qing,CAI Xiao-hua,REN Zhi-xiang

(School of Mechanical and Electrical Engineering,Central South University,Changsha 410083,China)

There are many factors which influence the vibration reduction effect of the ball-type automatic balancer when it is operating at the over-critical speed.In this paper,the mathematical model of the ball-type automatic balancer with installation eccentricity is established and the numerical simulation is done using the parameters determ ined by the experimental testing.Influence of the installation eccentricity on the vibration reduction effect of the ball-type automatic balancer is analyzed.The results show that the smaller the installation eccentricity is,the better the vibration reduction effect is.Within a certain range,improving the accuracy of the rotor’s processing and installation can significantly raise the vibration reduction effect for the ball-type automatic balancer.But over high accuracy of processing and installation may not be necessary since it does not help too much for improving the vibration reduction effect further.Result of the analysis may have application significance for vibration reduction of ball-type automatic balancers.

vibration and wave;installation eccentricity;ball-type automatic balancer;mathematical model; numerical simulation;vibration reduction

TB52；TH113.1

A

10.3969/j.issn.1006-1335.2014.01.019

1006-1355(2014)01-0082-06

2013-01-31

李镔桦（1988-），男，湖南慈利县人，在读硕士，目前从事自动平衡装置的减振研究。

E-mail:lbhailzx@qq.com