层状三元周期结构的带隙计算

陈源，李竞，黄涛，周明刚

(湖北工业大学湖北省汽车结构振动与噪声控制工程技术研究中心，武汉430068)

层状三元周期结构的带隙计算

陈源，李竞，黄涛，周明刚

(湖北工业大学湖北省汽车结构振动与噪声控制工程技术研究中心，武汉430068)

对于层状三元周期结构的带隙分析和研究目前还属空白。基于声子晶体理论，将层状三元周期结构简化为一维声子晶体结构，并利用集中质量法，分析了材料密度与材料阻尼比变化对第一带隙的影响。研究表明，材料密度的改变对第一带隙产生较大影响；材料阻尼比的变化对第一带隙影响不明显。研究结论为层状三元结构带隙设计提供了理论依据。

振动与波；声子晶体；层状三元周期结构；第一带隙

近年来，基于声子晶体理论的人工编织周期性结构的能带特性研究越来越受到人们的关注。这是由于通过人工编织的周期性结构，可使结构具有对经典波带通和带阻的特性。而如何利用周期结构中的带阻特性进行减振降噪，也已成为众多国内外研究人员的研究方向。由此，探索影响声子晶体带隙特性的因素，也成了摆在科研人员面前的重大课题。早在上世纪80年代，Achenbach等[1,2]人分析了弹性波在具有球形空腔的周期介质中的传播问题。Sigalas与Eeonomou[3]第一次从理论上证实了将实心球形材料埋入某一基体材料中形成的周期性点阵结构具有带隙特性。随后，众多学者[4,5]针对二维二元声子晶体结构，对密度、弹性模量、声阻抗与波速等材料参数与带隙的影响关系进行了研究。随着对各向异性材料、粘弹性材料以及一些新型功能材料如压电、压磁材料和形状记忆合金研究的深入，压电系数、介电常数、粘弹性阻尼系数和松弛时间等成为需要考虑的材料参数。Han等[6]专门研究了二维压电声子晶体中弹性参数、压电系数和介电常数对带隙的影响。Wei等[7]研究了一维粘弹性声子晶体，并给出了几组不同粘弹性阻尼系数和松弛时间下得到的带隙。Wu等[8]将功能梯度材料作为连接层应用于一维层状声子晶体当中，并讨论了加入功能梯度材料与不加入功能梯度材料时，带隙变化的情况。由此可见，现有文献对于声子晶体的研究已经有了很大的发展，但对于层状周期结构的带隙分析还停留在二元结构。本文将层状三元周期结构简化为一维声子晶体结构，利用集中质量法，分析了密度与材料阻尼比变化对第一隙的影响。

1 层状三元周期结构理论建模与计算

1.1 理论建模

三种材料按ABC顺序沿o x方向排列形成层状三元周期结构，如图1所示。

图1 层状三元周期结构示意图

若层状结构的非周期方向尺寸（层状周期结构的长度与宽度）远大于周期方向尺寸（层状周期结构的晶格常数），则该结构可视为一维声子晶体结构。同时，考虑有平面波在该结构中沿o x方向传播，并且平面波为纵波，此时，层状周期结构的振动情况与周期性弹簧振子结构类似。因此，运用集中质量法，将层状三元周期结构简化为周期性弹簧振子结构，如图2所示。

若材料具有粘弹性，对应的集中质量模型当中，质点与质点之间处除了具有刚度kj以外，还具有阻尼系数cj，如图3所示。

将一维声子晶体结构利用集中质量法简化为周期性弹簧振子结构后，应用牛顿第二定律得到系统的动力学微分方程。

图2 层状三元周期结构简化为多弹簧振子模型图

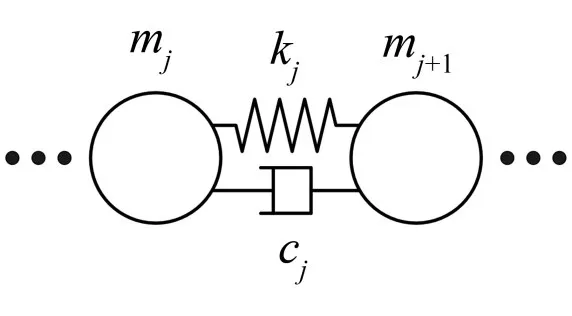
图3 含阻尼弹簧振子示意图

式中mj表示第j个质点的质量，kj-1与kj分别表示第j个质点左右两边的弹簧刚度，cj-1与cj分别表示第j个质点左右两边的阻尼系数，xj-1、xj与xj+1分别第j-1个、第j个与第j+1个质点的位移，x¨j表示第j个质点的加速度。

第j个质点的质量为

式中ρj表示第j个质点对应单元的密度，dj表示第j个质点对应单元的长度，S为层状结构的横截面积。

连接第j个质点与第j+1个质点的弹簧刚度kj

由式（3）与（4）给出

其中式（3）表示第j个质点与第j+1个质点同为材料A时的刚度计算，式（4）表示第j个质点与第j+1个质点分别为材料A与材料B时，两质点之间的刚度计算。

而阻尼系数cj与材料的阻尼比ζj有关

根据Block定理，在周期边界条件下，该质点运动方程的解可以设为振幅为Aj，角频率为ω的简谐振动

将（6）代入动力学微分方程组（1）化简得到一般的线性方程

观察方程（7）可以发现，当在j=0或n时，会使用到前一个周期和后一个周期中的参数，此时，需加入周期性边界条件

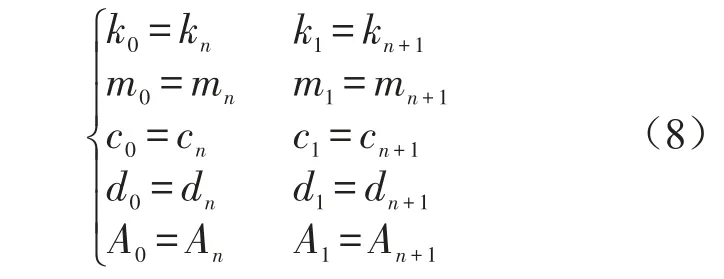
将周期性边界条件（8）代入线性方程（7），并用矩阵形式表示该线性方程组

可以发现，该振动特性方程组（9）中同时含有i ω和ω2项，不是标准的特征值方程，因而不能够直接求得其能带结构，需要进一步对方程经行相应的数学处理。

令λ=i ω则

将（10）与（11）代入矩阵方程（9）并化简得

联立方程组（11）（12），可得

1.2 层状三元周期结构算例

众所周知，若结构具有周期性，则该结构会出现弹性波带隙。层状三元周期结构是以三层材料作为一个原胞而形成的周期结构，因此这种结构必然存在着弹性波带隙。下面是一个层状三元周期结构的算例，每个原胞内的三层材料依次为：硅橡胶、铅、钨。材料具体参数如表一所示。

通过材料的弹性模量与泊松比，可以求得材料的拉梅常数。将参数带入到前文中的理论模型中，便可得到该结构的能带曲线。

从图4中，可以看出有阻尼的层状三元周期结构中的第一带隙，频率上限与下限分别为817 Hz与6 261 Hz，如果弹性波的频率属于这个区间，则弹性波将不会在该结构中传播。

图4 有阻尼层状三元周期结构能带图

2 结果与分析

针对层状三元周期结构的能带算法在前文中已经给出。本节主要研究由三种材料构成的层状三元周期结构，即ABC结构。讨论每层材料的密度和阻尼比变化对第一带隙的影响。

2.1 密度变化对带隙的影响

根据前文中所提供的算法，研究在ABC结构中，材料密度变化对第一带隙的影响，不计阻尼，计算所用材料参数如表一所示。

图5中（a）、（b）、（c）分别表示ABC结构中，三种材料密度变化对第一带隙关系。从图5（a）中可以发现，当材料A的密度增大时，第一带隙的上限频率向低频方向移动，下限频率基本保持不变，带隙宽度减小。从图5（b）（c）中可以发现，当材料B与材料C的密度增大时，第一带隙的上限频率基本保持不变，而下限频率略微向低频方向移动，带隙宽度增大。

表1 材料参数

2.2 阻尼比变化对带隙的影响

图6为ABC中材料A的阻尼系数对第一带隙的影响，计算所用材料参数如表1所示。当材料A的阻尼比由0增大到0.5时，第一带隙的上下限频率基本保持不变。可见，若将材料的粘弹性单纯由阻尼比来表示，则对带隙基本没有影响。

图5 ABC中密度变化对第一带隙的影响图

图6 ABC中材料A的阻尼系数对第一带隙的影响图

3 结语

本文首先对一维集中质量法进行了一定的改进，使该算法能够将材料的阻尼特性考虑在内。其次，利用改进后的算法对层状三元周期结构中每层材料密度的改变与较软材料阻尼比的改变对第一带隙的影响进行了讨论，并得到如下结论：

（1）对于较轻较软的材料，增加其密度，会使第一带隙的上限频率下降，带隙宽度减小；而对于较重较硬的材料，增加其密度，会使第一带隙的下限频率下降，带隙宽度增大；

（2）若将材料的粘弹性视为阻尼比，则阻尼比的变化对第一带隙基本没有影响。

致谢

感谢中国国家自然科学基金项目——人工编织周期性结构低频带隙机理的研究（No.50975081）和中国湖北省自然科学基金项目——周期性板壳工程结构的低频带隙机理研究（No.2011CDB085）对本文的支持。

[1]Achenbach J D,Kitahara M.Reflection and transmission of an obliquely incident wave by an array of spherical cavities[J].J.Acoust.Soc.Am.,1986,80:1209-1214.

[2]Achenbach J D,Kitahara M.Harmonic waves in a solid with a periodic distribution of spherical cavities[J].J.Acoust.Soc.Am., 1987,81:595-598.

[3]Sigalas M M,Economou E N.Elastic and acoustic wave band structure[J].Journal of Sound and Vibration,1992, 158:377-382.

[4]Sigalas M M,Economou E N.Band structure of elastic waves in two dimensional systems[J].Solid State Communications,1993,86:141-143.

[5]Chul Sik Kee,Jae Eun Kim,Hae Yong Park,et al.Essential role of impedance in the formation of acoustic band gaps[J].Journal of Applied Physics,2000,87:1593-1596.

[6]HAN J C,ZHAN Z Q,WEI P J.The influence of material constants on band gaps of piezoelectric phononic crystal [J].Proceedings of the 2008 Symposium on Piezoelectric, Acoustic Wave and Device Application,2008,360-363.

[7]ZHAO Y P,WEI P J.The band gap of 1 D viscoelastic phononic crystal[J].Computational Materials Science, 2009,46:603-606.

[8]WU Mei-ling,WU Liang-yu,YANG Wen-pei,et al.Elastic wave band gaps of one-dimensional phononic crystals with functionally graded materials[J].Smart Material and Structures,2009,18:115013.

Analysis of the Band Gap of a Layered Triple Periodic Structure

CHEN Yuan,LI Jing,HUANG Tao,ZHOU M ing-gang

(Research Center of Noise&Vibration Control forAutomotive Structural Engineering of Hubei, Hubei University of Technology,Wuhan 430068,China)

Currently,researches of band gap analysis are mainly focused on layered binary periodic structure.In this paper,band-gap of the layered triple periodic structure is studied.First of all,this structure is simplified to a one-dimensional phononic crystal structure based on phononic crystal theory.Then,the effect of density and damping ratio of the material on the first band gap is analyzed using lumped-mass method.The results indicate that the effect of the density of material on the first band gap is considerable,while the effect of damping ratio of material is insignificant.This conclusion may provide a theoretical basis for band gap design of layered triple periodic structure.

vibration and wave;phononic crystal;layered triple periodic structure;the first band-gap

A

10.3969/j.issn.1006-1335.2014.01.005

1006-1355(2014)01-0019-04

2013-02-27

国家自然科学资助项目（基金编号：50975081）；湖北省自然科学资助项目（基金编号：2011CDB085）

陈源（1971-），男，博士，目前从事振动与噪声控制研究。

E-mail:cy17220@163.com