三叶孔板换热器热力性能及其影响因素分析

朱凌云，杨锦春，周帼彦，谭祥辉，郭震，朱辉，郎红方，朱冬生

（1 华东理工大学承压系统与安全教育部重点实验室，上海 200237；2 深圳中广核工程设计有限公司，

广东 深圳 518031）

管壳式换热器凭借结构简单、制造方便、适用范围广等特点，被广泛应用在化工、炼油、电站等行业。传统的弓形折流板换热器有壳程压降大，存在流动“死区”，易产生流体诱导振动等缺点[1-3]。为了响应国家节能减排政策，许多新型换热器应运而生并有望代替传统弓形折流板换热器。三叶孔板换热器作为一种新型异形孔板换热器，流体在其壳程呈纵向流动，因而具有传热效率高、流动“死区”少、抗振性能好等优点，被广泛地应用在核电等行业。

目前，采用数值模拟方法对换热器传热性能进行研究时，主要包含两种模型：整体模型和局部模型。采用整体模型进行数值模拟可以得到较为准确的流场和温度场信息，但一方面其模型建立相对复杂，另一方面整体模型的求解对计算机性能要求高，计算时间较长。局部模型又分周期性全截面模型和“单元流道”模型。周期性全截面模型既能保证计算精度又可以提高计算效率，其运用在诸多换热器数值模拟的准确性已经得到证实[4-8]。文献[9]的研究结果表明，三叶孔板换热器壳程流体流过第一块支撑板后，已达到充分发展，后面的流动及传热随着壳程结构的周期性而呈现周期性变化。

为了提高计算效率，本文在结构分析的基础上，建立了三叶孔换热器壳程流体流动的周期性全截面模型，采用商业软件Fluent14.0，对8 种结构参数不同的三叶孔换热器壳程传热性能进行数值研究，进一步分析支撑板间距Lb、开孔高度H 以及导流筒形式等结构参数对三叶孔板换热器热力性能的 影响。

1 三叶孔板换热周期性模型

运用周期性全截面模型对三叶孔板换热器进行数值计算前，先作如下假设：①壳程流体流动为稳态湍流；②忽略换热管与支撑板以及支撑板与壳体之间的流体漏流；③换热管壁为恒定温度；④壳体与外界环境绝热。

1.1 物理模型

为了减小进出口对流动和换热的影响，选取了包含2 块支撑板在内的几何模型。考虑到结构对称性，数值模拟中取一半作为计算模型，三叶孔板换热器壳程周期性全截面模型如图1 所示。

选取不同支撑板间距、不同三叶孔孔高和不同导流筒形式的模型分别进行数值研究，换热器模型结构如图2 所示。其中模型1-1、模型1-2、模型1-3、模型1-4 具有相同三叶孔孔高、不同的支撑板间距； 模型1-2、模型2-2、模型3-2、模型4-2 具有相同的支撑板间距、不同的孔高；模型1-2 和模型0 分别为六边形和圆形导流筒。具体结构参数及几何尺寸见表1。

图1 三叶孔板换热器壳程周期性全截面模型

图2 不同结构的换热器模型

1.2 控制方程和边界条件

三叶孔板换热器壳程内流体为单相连续不可压缩流体，在不考虑体积力的情况下，应满足如式（1）通用控制方程[10]。

式中，Гφ和Sφ分别为广义扩散系数和广义源项。当φ取1，U、T 和k、ε 等不同变量时，方程分别代表了连续性方程、动量方程、能量方程和湍流模型方程。

进出口采用周期性边界条件。对于周期性充分发展的流动和传热，其速度和压力具有以下特点，见式（2）～式（5）[10-12]。

对于换热管为恒定温度，流体流动充分发展后流体的量纲为1 温度为式（6）。

式中，Θ 为量纲为1 温度，遵循周期性边界条件 Θ( r ,0 ) =Θ( r ,s )； s 为 周 期 长 度 ；

选取水作为壳程流体介质，入口温度为283K，其物性参数由piecewise-linear[13]分段线性插值给出。壳体壁面、支撑板面均设为绝热面，换热管壁面采用恒壁温边界条件，温度为Tw=307K。

1.3 网格划分及数值方法

充分考虑支撑板处流体流动的复杂性，将周期性全截面模型分成远离支撑板区域和支撑板附近区域两块，采用ANSYS Workbench 的Meshing 进行分块划分处理。在远离支撑板的几何区域，采用六面体结构化网格；在支撑板附近区域采用四面体网格，并加密处理，具体网格划分情况如图3 所示，其中图3(a)为壳程中间横截面上网格，图3(b)为支撑板附近纵截面上网格。

图3 周期性全截面模型网格划分

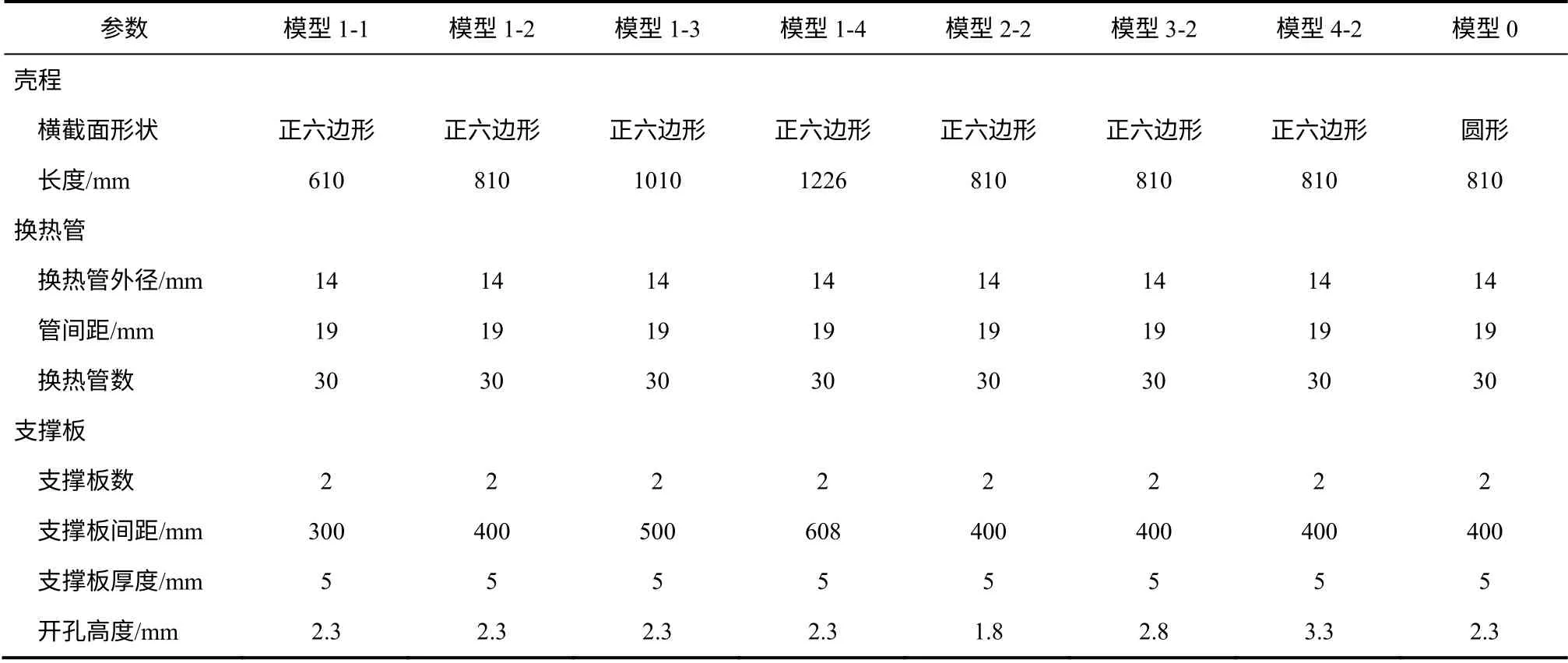
表1 不同模型的几何参数

采用基于有限体积法的Fluent14.0 对各模型进行数值计算。其中，压力与速度采用SIMPLE 耦合算法，压力项采用标准格式离散[14]，其他项采用二阶迎风格式[15]。连续性方程、动量方程、k 方程和ε方程收敛残差均为10-6，能量方程的收敛残差设置为10-8。

为确保计算的准确性，需进行网格无关性验证。以壳程流量为15.6kg/s 的模型1-2 为例，采用5 种不同数量（3.01×106、3.88×106、4.47×106、5.23×106、6.00×106）的网格模型对其壳程传热系数h 和压降Δp 进行了数值计算，结果如图4 所示。由图4 可见，最后3 套网格计算出的传热系数h 和压降Δp 分别为9561.7W/(m2·K)，55.9kPa；9612.3W/(m2·K)，55.5kPa；9638.6W/(m2·K)，55.3kPa，结果相差均在2%以内。综合考虑计算精度和计算效率，选用单元数为4.47×106网格模型进行计算分析。

图4 不同网格数计算出来的壳程传热系数及压降

2 计算结果分析

2.1 支撑板间距对传热及压降影响

在三叶孔高相等的情况下，壳程传热系数和压力梯度随支撑板间距的变化关系如图5 所示。

由图5 可以看出，在相同壳程质量流量下，壳程传热系数和压降都随着支撑板间距的增大而逐渐减小，且减小速度逐渐变慢。以壳程质量流量为30.6kg/s 为例，支撑板间距从300mm 增大到400mm时，传热系数减小12.3%，压力梯度减小21.4%；从400mm 增大到500mm 时，传热系数减小10.9%，压力梯度减小23.3%；从500mm 增大到608mm 时，传热系数减小6.2%，压力梯度减小16.7%。当壳程质量流量为6.2kg/s 时，支撑板间距从300mm 增大 到400mm 时，传热系数减小12.8%，压力梯度减小22.5%；从400mm 增大到500mm 时，传热系数减小6.1%，压力梯度减小19.6%；从500mm 增大到608mm 时，传热系数减小7.8%，压力梯度减小18.4%。由此可见，随着流量逐渐增大，壳程传热系数和压降都随着支撑板间距的递减速度增加；支撑板间距对压降的影响大于其对传热的影响。

图5 支撑板间距对传热及压降的影响

2.2 三叶孔孔高对传热及压降影响

在相同支撑板间距的情况下，对不同三叶孔孔高模型的数值计算结果如图6 所示。由图6 可知，随着三叶孔孔高的增大，壳程流体传热系数及压力梯度都逐渐减小。这是由于在壳程流量不变的情况下，较小的开孔高度有利于提高流体流过三叶孔时的射流流速，可以更好地冲刷换热管壁，减薄流动边界层，从而加强了局部区域内流体的换热。然而，较小的开孔高度对流体流动阻力也相应增大，流体流过支撑板的局部动量损失也增大。从图6 还可以看出，三叶孔孔高对壳程压降的影响大于其对传热的影响。当壳程质量流量为30.6kg/s 时，开孔高度从1.8mm 增大到3.3mm 时传热系数减小了20.4%，压力梯度减小了66.9%；而壳程质量流量为6.2kg/s时，相应的传热系数减小了20.6%，压力梯度减小了67.4%。因此，在满足传热的条件下，可以适当增加三叶孔的开孔高度，以减少泵的功耗。由于开孔高度受限于换热管间距（图2），考虑本文换热管间距为19mm，文中开孔高度最大取为3.3mm。

图6 三叶孔孔高对传热及压降的影响

2.3 导流筒形式的影响

在三叶孔板间距以及开孔高度相同的情况下，不同结构的导流筒对传热及压降性能影响也很大。为了研究不同导流筒换热器传热及压降性能的差异，选取了两种不同模型进行对比。模型1-2 为六边形导流筒，模型0 为圆形导流筒，具体尺寸详见表1。图7 为两种模型壳程传热系数与压力梯度随质量流量的变化关系。从图7 中可以看出：支撑板间距及开孔高度都相同的情况下，六边形导流筒换热器壳程传热系数比圆形导流筒的约大7%，同时压降约大4%。

图8 所示为两种不同导流筒壳程x=8mm 纵截面上流场分布。可以看出，圆形导流筒换热器支撑板尾部流动“死区”比六边形的范围大，使壳程有效流道减小，因此换热性能比六边形导流筒差。

2.4 综合性能分析

图9 为壳程传热系数随压力梯度的变化关系，从图中可以看出，在相同的压力梯度下，模型4-2 的传热系数最大，模型2-2 的传热系数最小。

图7 导流筒结构对换热及压降的影响

为了比较不同支撑板间距、不同开孔高度和不同导流筒形式的三叶孔板换热器壳程传热性能，综合考虑传热和压降的影响，定义综合性能指标η 为单位压力梯度下的传热系数由定义可知，η 值越大，综合性能越好。

图10所示为8种不同结构换热器综合性能指标与壳程质量流量的变化关系。由图10 可知，随着壳程质量流量的增加，不同结构换热器的η 值均减小。在相同壳程质量流量下，模型4-2 的η 值最大，综合性能最好，模型2-2 的η 值最小，综合性能最差。因此，在壳程质量流量较小的工程应用中，可设计较大的开孔高度以获取较好的综合性能，而支撑板间距的选取，则需要结合开孔高度进行综合评估。

3 结 论

本文建立了三叶孔板换热器壳程流体流动和传热的周期性全截面模型，并运用该模型对8 种不同结构参数的三叶孔板换热器进行了数值研究，分析了支撑板间距、开孔高度以及导流筒形式对其壳程流动及传热性能的影响，初步得出以下结论。

图8 两种导流筒壳程x=8mm 纵截面上流场分布

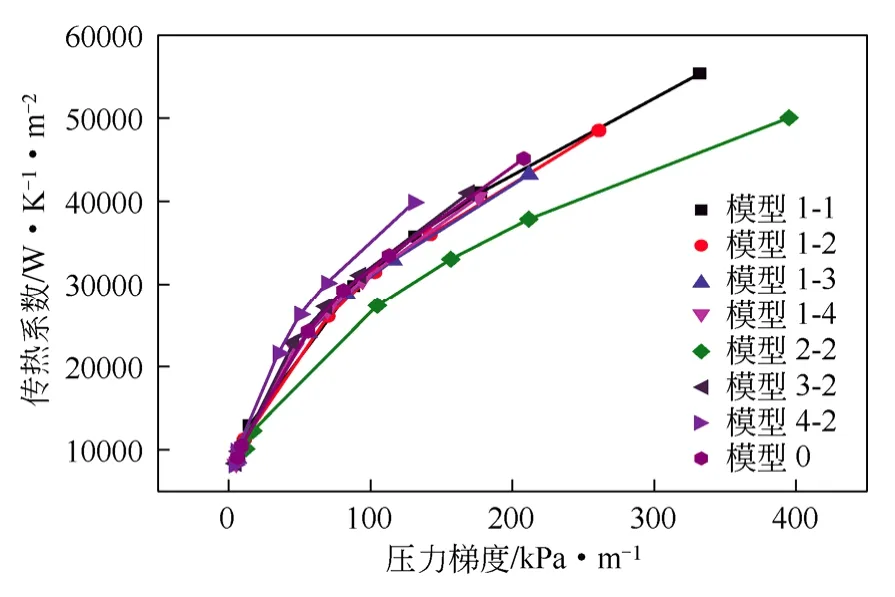
图9 传热系数随压力梯度的变化关系

图10 综合性能随壳程流量的变化关系

（1）在其他结构参数一定的条件下，三叶孔板换热器壳程传热系数与压力梯度随着支撑板间距（或开孔高度）的增加而减小；支撑板间距（或开孔高度）对三叶孔板换热器壳程压降的影响大于其对传热的影响。

（2）六边形结构的导流筒换热器壳程流体流动“死区”比圆形导流筒换热器小，流体流动分布更均匀，因此前者传热性能比后者好。

（3）在本文研究的8 种不同结构的换热器中，模型4-2（支撑板间距为 400mm，开孔高度为3.3mm）综合性能最好，模型2-2（支撑板间距为400mm，开孔高度为1.8mm）最差。因此，在壳程流量较小的工况下，对支撑板结构进行工程设计时，可选取较大开孔高度，并结合开孔高度选择合适的支撑板间距，以获取综合性能较好的换热器设计 方案。

符 号 说 明

H——开孔高度，mm

h——壳程传热系数，W/(m2·K)

L——计算模型长度，m

Lb——支撑板间距，m

M——壳程流量，kg/s

p——壳程流体压力，kPa

Δp——壳程流体压降，kPa

s——周期长度，mm

T——流体温度，K

Tw——管壁温度，K

U——壳程流体和速度，m/s

u——壳程流速在x 轴上的分量，m/s

v——壳程流速在y 轴上的分量，m/s

w——壳程流速在z 轴上的分量，m/s

Θ——量纲为1 温度

η——综合性能指标

[1] 钱才富，高宏宇，孙海阳. 曲面弓形折流板换热器壳程流体流动与传热[J]. 化工学报，2011，62（5）：1233-1238.

[2] 邓斌，陶文铨. 管壳式换热器壳侧湍流流动与换热的三维数值模拟[J].化工学报，2004，55（7）：1053-1059.

[3] 黄文江，张剑飞，陶文铨. 弓形折流板换热器中折流板对换热器性能的影响[J]. 工程热物理学报，2007，28（6）：1022-1024.

[4] Zhang J F，He Y L，Tao W Q. 3D numerical simulation on shell-and-tube heat exchangers with middle-overlapped helical baffles and continuous baffles-Part Ⅱ：Simulation results of periodic model and comparison between continuous and noncontinuous helical baffles[J]. International Journal of Heat and Mass Transfer，2009，52（23-24）：5381-5389.

[5] Taher F N，Movassag S Z，Razmi K，et al. Baffle space impact on the performance of helical baffle shell and tube heat exchangers[J]. Applied Thermal Engineering，2012，44：143-149.

[6] You Y H，Fan A W，Lai X J，et al. Experimental and numerical investigations of shell-side thermo-hydraulic performances for shell-and-tube heat exchanger with trefoil-hole baffles[J]. AppliedThermal Engineering，2013，50（1）：950-956.

[7] 古新，董其伍，王珂. 基于三维实体模型的管壳式换热器壳程流场和温度场数值研究[J]. 压力容器，2008，25（5）：1-5.

[8] 王定标，王宏斌，梁珍祥. 扭曲三叶管传热与流阻性能的数值研究[J]. 化工学报，2012，63（7）：2064-2069.

[9] 朱凌云，郎红方，周帼彦，等. 三叶孔板换热器壳程流动及传热数值模拟[J]. 化工学报，2014，65（3）：829-835.

[10] 陶文铨. 数值传热学[M]. 第2 版. 西安：西安交通大学出版社，2001.

[11] Patankar S V，Liu C H，Sparrow E M.Fully developed flow and heat transfer in ducts having streamwise-periodic variations of cross-sectional area[J]. ASME Journal of Heat Transfer，1977，99（2）：180-186.

[12] Gong L，Li Z Y，He Y L，et al.Discussion on numerical treatment of periodic boundary condition for temperature[J]. Numerical Heat Transfer，Part B：Fundamentals，2007，52（5）：429-448.

[13] Fluent14.0 User’s Guide[M].ANSYS，Inc.，2011.

[14] 杨世铭，陶文铨. 传热学[M]. 第3 版. 北京：高等教育出版社，1998.

[15] Barth T J，Jespersen D C. The design and application of upwind schemes on unstructured meshes[J].AIAA Paper，1989，89（366）：1-12.