一般半刚性节点连接框架结构分析方法
段树金, 王 冉,2, 金坎辉,3
(1.石家庄铁道大学 土木工程学院,河北 石家庄 050043;2.聊城市规划建筑设计院有限公司,山东 聊城 252000;3.河北工程技术高等专科学校,河北 沧州 061001)
一般半刚性节点连接框架结构分析方法
段树金1, 王 冉1,2, 金坎辉1,3
(1.石家庄铁道大学 土木工程学院,河北 石家庄 050043;2.聊城市规划建筑设计院有限公司,山东 聊城 252000;3.河北工程技术高等专科学校,河北 沧州 061001)
研究对象为任意节点连接和任意支撑的平面框架。一般梁单元由等截面直杆及其杆端的轴向弹簧、切向弹簧和转动弹簧组成,推导得到此类单元的刚度矩阵、单元在8种基本荷载作用下的等效节点荷载。采用Matlab语言编写了适用于一般节点非线性连接框架的静力分析程序,非线性形式为指数函数或多项式函数,可以得到结构不同连接刚度下的节点位移、杆端位移和杆端力。算例显示出节点柔度对结构受力和变形的影响。
平面框架;半刚性节点;三弹簧模型;单元刚度矩阵;等效节点荷载;非线性分析
0 引言
焊接节点钢结构在强震作用下易发生脆性破坏,而采用角钢、螺栓端板、T形板等半刚性节点连接形式替代刚性连接节点,可以优化分配结构体系的内力、增大结构阻尼、减小结构振幅、降低地震作用对结构的危害[1]。目前,国内外关于钢结构半刚性连接的研究主要集中在框架梁柱连接节点的转动半刚性方面。王新堂[2]在梁单元杆端引入虚拟旋转弹簧推导单元刚度,得到了平面杆系结构的统一计算模型。
刘洋 等[3]认为实际结构中半刚性节点不仅具有转动半刚性,而且沿切向和轴向也有一定半刚性,并推导得到了考虑节点转动半刚性和切向半刚性的单元刚度矩阵和质量矩阵。胡吉安等研究了梁段拼接问题,将拼接节点设计成半刚性,提出的耗能拼接节点具有和梁相同的初始转动刚度,在正常使用阶段不允许拼接处高强螺栓出现滑移,而在弹塑性阶段利用拼接处的高强螺栓滑移耗能,可以提高框架结构整体抗震性能[4]。长孔螺栓节点可用于钢框架中的梁柱连接,代替焊接,提高节点处的延性,避免节点处的应力集中和脆性破坏,梁柱连接处的转动变形带动长孔螺栓节点产生摩擦耗能。在风荷载和小震作用下,高强螺栓拼接节点不发生滑移,主体结构处于弹性状态,满足正常使用要求;在大震作用下,拼接板产生滑动,不仅消耗大量地震能量,而且在滑动过程中还改变了原结构的自振频率和基本振型,减小结构振幅[5]。
柱的拼接研究方面,Snijder et al[6]进行的分析与试验研究结果表明拼接柱的承载力低于完整柱的承载力;Lindner[7]讨论了柱的3种拼接方式(端板连接、翼缘腹板盖板连接、翼缘盖板连接),进行模型试验和有限元数值分析,将拼接处的不完全连接用倾角和滑移缺陷表示,给出了承载力计算的近似公式。Baniotopoulos[8]研究了螺栓端板拼接的分离问题,建立了数学力学模型和有限元数值模型。
Ihaddoudene et al[9]在有限元模式中提出采用三弹簧模型,但在推导单元刚度矩阵和载常数时只考虑了节点的转动半刚性,而并未计及切向和轴向半刚性的影响。Coelho et al[10]研究了拼接柱的稳定问题,采用了考虑转动和切向半刚性的两弹簧模型,得到了拼接钢柱的临界荷载。
Landon et al[11]将半刚性节点的概念引入支座,把双角钢焊接连接归结为半刚性支撑,并采用三弹簧表示,通过试验确定了弹簧参数。Duan et al[12]提出的榫卯连接钢框架体系在动载作用下节点处会产生滑移、挤压和碰撞,从而起到耗能减震的作用,可以模型化为半刚性节点连接框架。另外,切向半刚性连接的概念已被引入钢-混凝土组合梁界面的连接[13-14];而柔性支座(包括转动、切向和轴向)与半刚性节点连接属于同一类问题,可以一并研究,有利于结构体系的优化。
因此,建立一种统一的节点为任意连接的平面杆系计算模型具有重要的理论和现实意义。从平面杆单元的刚度方程出发,通过在杆端引入虚拟转动、切向和轴向弹簧,由严格的数学方法得到一般平面杆系结构的统一计算模型。
1 单元刚度矩阵和等效节点荷载推导
1.1 单元模型和基本假定
图1为具有一般半刚性连接的平面梁单元,即在梁端引入了一个转动弹簧和两个线弹簧来模拟节点处的转动、轴向和切向半刚性,K(θ)、K(x)和K(y)分别表示转动刚度、轴向刚度和切向刚度与对应位移的关系函数,其关系可以是线性的,也可以是非线性的;刚度无穷大代表刚接,刚度为零代表铰接。图1中梁单元,E为弹性模量,I为截面惯性矩,A为截面面积,l为杆长,i为线刚度。

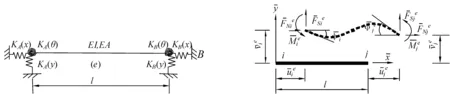
图1 一般半刚性连接平面梁单元 图2 杆端力及杆端位移
1.2 单元刚度矩阵
1.2.1 轴向刚度
设单元杆端分别发生轴向位移ΔA、ΔB,轴向弹簧线位移ΔUA、ΔUB,连接刚度UKA、UKB与单元端部轴力NA、NB的关系为ΔUA=NA/UKA,ΔUB=NB/UKB, 忽略剪力和弯矩对轴力的影响,可得轴力与节点轴向位移的关系为
(1)
由此可得
(2)

1.2.2 剪切和弯曲刚度
同时考虑单元的节点转动和切向半刚性。
(1)设单元杆端分别发生转角位移θA、θB,螺旋弹簧相对转角θrA和θrB,连接刚度RKA、RKB以及单元端部弯矩MA、MB的关系为θrA=MA/RKA,θrB=MB/RKB;竖向弹簧的线位移ΔrA、ΔrB,连接刚度KA、KB以及单元端部剪力QA、QB的关系为ΔrA=QA/KA,ΔrB=QB/KB,可得刚度方程
(3)
(4)
化简可得
(5)
式中,
(2)设单元两端发生相对线位移Δ,考虑节点转动和剪切半刚性的刚度方程为
(6)
即,
(7)
式中,
因此,一般半刚性节点连接单元的刚度矩阵可以表示为
(8)

1.3 单元固端力
基于1.1的假设,可以得到任意荷载作用下一般半刚性连接单元两端的固端力。
(1)集中荷载(图3)。
(9)
(10)
式中,
D1=pRKA(KAKBRKBl2ab2+2iKAKBl2a2b+4iKAKBl2ab2+6iKBRKBab2-6iKARKBa2b+
6iKARKBal2+6iKARKBa2b+6iKARKBab2-6iKBRKBl2b-12i2KBl2b+12i2KAl2a);
D2=-pRKB(KAKBRKAl2a2b+2iKAKBl2ab2+4iKAKBl2a2b-6iKARKAal2+6iKBRKAl2b+
6iKARKAa2b+6iKARKAab2+6iKBRKAa2b+6iKBRKAab2+12i2KBl2b-12i2KAl2a);
D=l2(RKAKAl2KBRKB+4RKBiKAl2KB+4iRKAKAl2KB+12KARKBi2+12KBRKBi2+
12KAi2RKA+12KAKBi2l2+12RKBiRKAKA+12RKBiRKAKB+12KBi2RKA)。
(2)均布荷载(图4)。

图3 集中荷载作用 图4 均布荷载作用
(11)
(12)
式中,
D1=ql2RKA(KKAl2KBRKB+6iKAl2KB-24iKBRKB+48iKARKB+72i2KA-72i2KB);
D2=ql2RKB(-KAl2KBRKA-6iKAl2KB+24iKARKA-48iKBRKA+72i2KA-72i2KB);
D=12(12i2KBRKB+12i2KARKB+12i2KBRKA+12i2KARKA+12i2KAl2KB+
KAl2KBRKARKB+12RKBiKBRKA+12RKBiKARKA+4RKBiKAl2KB+4iRKAKAl2KB)。
(3)三角形分布荷载(图5)。
(13)
MA=D12D,MB=D2D
式中,
(14)
D1=ql2RKA(3KAKBRKBl2+16iKAKBl2+90iKARKB-90iKBRKB+120i2KA-240i2KB);
D2=ql2RKB(-KAKBRKBl2-7iKAKBl2+15iKARKA-75iKBRKA+60i2KA-120i2KB);
D=30(12i2KBRKB+12i2KARKB+12i2KBRKA+12i2KARKA+12i2KAl2KB+
KAl2KBRKARKB+12RKBiKBRKA+12RKBiKARKA+4RKBiKAl2KB+4iRKAKAl2KB)。
(4)集中力偶(图6)。

图5 三角形分布荷载作用 图6 集中力偶作用
(15)
MA=D1D,MB=D2D
式中,
(16)
D1=mRKA(-l2bKAKBRKB+2l2KAKBia-6liKBRKB+3lbKAKBRKBa+6ilKAKBba+6KBiaRKB-
4l2KAKBib-6KAibRKB-12lKAi2-12lKBi2-6liKARKB+6KAiaRKB-6KBibRKB);
D2=-mRKB(4l2KAKBia+l2KAKBRKAa-2lKAKBib-6lKAKBiba-3lKAKBRKAba+
6liKARKA+12lKAi2+6liKBRKA+12lKBi2+6KAiRKAa-6KAiRKAb+6iRKAKBa-6iRKAKBb);
D=l(12i2KBRKB+12i2KARKB+12i2KBRKA+12i2KARKA+12i2KAl2KB+
KAl2KBRKARKB+12RKBiKBRKA+12RKBiKARKA+4RKBiKAl2KB+4iRKAKAl2KB)。
(5)分布力偶(图7)。
(17)
MA=D1D,MB=D2D
(18)
式中,
D1=mRKA(2l3KAKBRKB+8l3KAKBi-12i2lKA-12i2lKB+6ilKARKB+6ilRKBKB);
D2=-mRKB(18ilKA+18ilKB+24i2lKA+24i2lKB+2l3iKAKB);
D=12i2KBRKB+12i2KARKB+12i2KBRKA+12i2KARKA+12i2l2KAKB+
l2KAKBRKARKB+12iRKARKBKB+12iRKARKBKA+4iRKBKAKBl2+4iRKAKAKBl2。
(6)轴向集中荷载(图8)。

图7 分布力偶作用 图8 轴向集中荷载作用
(19)
式中,
(7)轴向均布荷载(图9)。
(20)
式中,
(8)温差(图10)。

图9 轴向均布荷载作用 图10 温差作用
(21)
MA=EIα(t2-t1)(RKARKB+6iRKA)h(4RKBi+4RKBi+RKARKB+12i2),MB=-EIα(t2-t1)(RKARKB+6iRKA)h(4iRKB+4iRKB+RKARKB+12i2)(22)
2 算例
采用Matlab语言编写了适用于非线性节点连接框架静力问题的一般分析程序,非线性形式为指数函数或多项式函数,可以得到结构不同连接刚度下的节点位移、杆端位移和杆端力。

分别对以上3种连接方式的框架结构进行加载计算,求得结构在各个荷载步下的水平位移,如图12所示。从中可以看出,柱脚处采用半刚性连接的结构在滑移出现前,表现出近乎刚接的特性,呈现直线变化,当荷载增加到一定值时,柱脚开始滑动,刚度降低,呈现出非线性;而梁柱节点采用转动半刚性连接的结构其各个荷载步下的位移都比较大,只有在加载初期呈现线性,之后呈现非线性变化。

图11 结构形式及节点单元编号图(单位:m) 图12 不同连接方式下结构的荷载位移曲线
当水平荷载为310 kN时,以上三种连接方式的结构弯矩图如图13所示。可以看出,柱脚采用切向半刚性连接以后结构的弯矩图与完全刚接的结构弯矩图相近,各个梁柱的弯矩大小以及变化趋势几乎是相同的,横梁上的弯矩均比较大,整个结构的最大值598 kN·m出现在柱脚处。梁柱节点考虑了转动半刚性以后横梁上的弯矩大大减小,梁端弯矩约为刚接时弯矩的1/3,但是柱子上的弯矩逐步增大,特别是在柱脚处,弯矩达到998 kN.m,相比刚性连接的情况弯矩大幅度增加,整个结构出现了内力重分布。

图13 三种节点连接形式下的结构弯矩图(单位:kN·m)
采用ANSYS软件中的Combin39非线性弹簧单元模拟节点的半刚性连接[15],对算例进行验证,得到了完全相同的结果,在此不予赘述。
3 结论
(1)提出了可以同时考虑节点轴向、剪切和弯曲变形性能的三弹簧梁单元模型,推导得到了单元刚度矩阵以及不同荷载作用下的单元固端力。模型适用于所有节点连接形式和各种支座;进行结构分析时不会增加结构单元的数量或方程的阶数。
(2)运用Matlab语言编写了节点半刚性连接非线性分析通用程序。算例表明节点或支座为半刚性连接时对结构受力的影响不容忽视;可以构造初期为刚性、后期为半刚性的节点连接,以对应不同的受力阶段。
(3)这一算法的提出为完善半刚性节点连接钢框架设计及结构减震耗能优化提供了理论依据。
[1]GE KH. Effect of connections on frames [J]. Journal Constructional Steel Research, 1988(10):241-267.
[2]王新堂.平面杆系结构静力分析的统一模型[J]. 力学与实践,2003, 25(3):41-43.
[3]刘洋,段忠东,周道成. 利用一种混合梁单元修正结构半刚性节点及边界条件[J]. 振动与冲击, 2009,28(9):39-47.
[4]王斌,李启才. 悬臂梁段拼接节点耗能的刚性钢框架时程分析[J]. 西安科技大学学报,2011,31(4):433-437.
[5]胡吉安,李启才,刘刚. 钢结构拼接节点的耗能性能分析[J]. 苏州科技学院学报:工程技术版,2009,22(1):19-22.
[6]Snijder H H, Honenderkamp J C D. Influence of end plate splices on the load carrying capacity of columns [J]. J. Constr. Steel Res., 2008(64): 833-844.
[7]Lindner J. Old and new solutions for contact splice in column [J]. J. Constr. Steel Res., 2008(64): 833-844.
[8]Baniotopoulos C C. On the separation process in bolted steel splice plates [J]. J. Constr. Steel Res., 1995(32):15-35.
[9]Ihaddoudene A, Saidani M, Chemrouk M. Mechanical model for the analysis of steel frames with semi rigid joints [J]. J. Constr. Steel Res., 2009(65): 631-640.
[10]Coelho A M G, P D Simao, S S K Bijlaard. Stability design criteria for steel column splices [J]. J. Constr. Steel Res., 2010(66): 1261-1277.
[11]Landon G S, Schleyer G K. Modelling the response of semi-rigid supports under combined loading [J]. Engneering Structures, 2004(26):511-517.
[12]Duan S J, Suo W Q, Yu Y,et al. Model test on a kind of assembly steel frame with mortise and tennon joints[C]// Sai On Cheung, et al. Modern Methods and Advances in Structural Engineering and Construction (ISEC-6, Zurich).Singapore: Research Publishing, 2011:721-726.
[13]Qi J J, Jiang L Z. Effects of interface slip and semi-rigid joint on an elastic seismic response of steel-concrete composite frame [J]. J. Cent. South Univ. Technol. 2010,17(6):1327-1335.
[14]Duan S J,Niu R M, Xu J,et al. A finite element model for double composite beam [C]// Nader G.. Challenges,Opportunities and Solutions in Structrual Engineering and Constructions (ISEC-5, Las Vegas,2009) . London: Taylor & Francis Group, 2010: 197-202.
[15]金坎辉. 一种新型柱脚连接方式的受力分析及应用[D]. 石家庄:石家庄铁道大学土木工程学院,2012.
(责任编辑 刘宪福)
Analysis Method for Planar Frames with Generalized Semi-Rigid Connections
Duan Shujin1, Wang Ran1,2, Jin Kanhui1,3
(1.School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043,China;2.Liaocheng city planning and Architectural Design Institute Co., Ltd,Liaocheng 252000, China;3.Hebei Engineering and Technical College,Cangzhou 061001,China)
The planar frame with arbitrary connections and supports is studied. A new beam element is proposed, which consists of uniform bar and three null length springs (along rotational, transverse and axial direction) at each end. The stiffness matrix of the element and equivalent nodal forces subjected to eight kinds of different loads are derived. A program is compiled in Matlab language for calculation of static mechanical behaviour of generalized frame, in which the connection nonlinear relationship is expressed as exponential function or polynomial function. the results of the rigid frame and the semi-rigid frames are Compared, showing the influence of connection flexibilities on structure forces and deformation.
planar frame; semi-rigid joint; three-springs mechanical model; stiffness matrix of element; equivalent nodal force vector;non-linear analysis
10.13319/j.cnki.sjztddxxbzrb.2014.03.01
2013-06-04
段树金 男 1955年出生 教授
TU311
A
2095-0373(2014)03-0001-08

