高速数控机床主轴用角接触球轴承接触特性研究

张世兵，马伟，李济顺，薛玉君

(河南科技大学 河南省机械设计及传动系统重点实验室，河南 洛阳 471003)

高速数控机床主轴用角接触球轴承的精度等级一般在P4以上，油润滑[1]工况下，dm·n值一般为1.0×106～2.5×106mm·r∕min。角接触球轴承在高速运转时将产生很大的离心力和陀螺力矩，离心力使钢球与沟道的接触应力和接触角发生改变；陀螺力矩使钢球绕自身轴线旋转，而当其大于沟道接触部位的摩擦力矩时，钢球发生滑动[2]。

在高速、急开、急停等特殊工况下，离心力、陀螺力矩、摩擦、热变形等因素严重影响轴承的运动稳定性，使其内部运动形式变得异常复杂。文献[3]基于外圈沟道控制理论，指出当接触面的摩擦因数足够大时可避免陀螺力矩引起的滑动，但把外圈的摩擦因数设为定值。文献[4]提出克服陀螺枢轴滑动的摩擦力矩与钢球到内、外圈距离的比例有关，但忽略了外界因素对摩擦力矩的影响。文献[5]通过测量磁通量的变化研究了钢球的运动状态，但是试验比较复杂。文献[6]建立了高速主轴-轴承有限元模型，但忽略了转子及轴承离心力的影响。文献[7]基于Timoshenko梁建立了高速主轴系统的有限元模型，研究了轴承预紧和工作温升对主轴动态特性的影响，但忽略了轴承转速的影响。在此，综合考虑转速、受力、润滑、摩擦、接触情况等多种因素，建立高速轴承力学模型，以预测陀螺力矩、接触载荷及摩擦因数的变化规律，为研究轴承的运动特性提供依据。

1 力学模型的研究

假定轴承内部变形均为弹性接触变形，符合Hertz弹性接触理论的变形规律，内、外圈在外载荷下只发生刚性位移。

1.1 轴承力学模型

轴承受力如图1所示。Fx，Fy，Fz分别为轴承受到的x，y，z方向上的力；Mx，My分别为轴承受到x，y方向的力矩；Ψj为球的位置角；j为球的位置编号，以y轴正方向起，按逆时针方向编号。

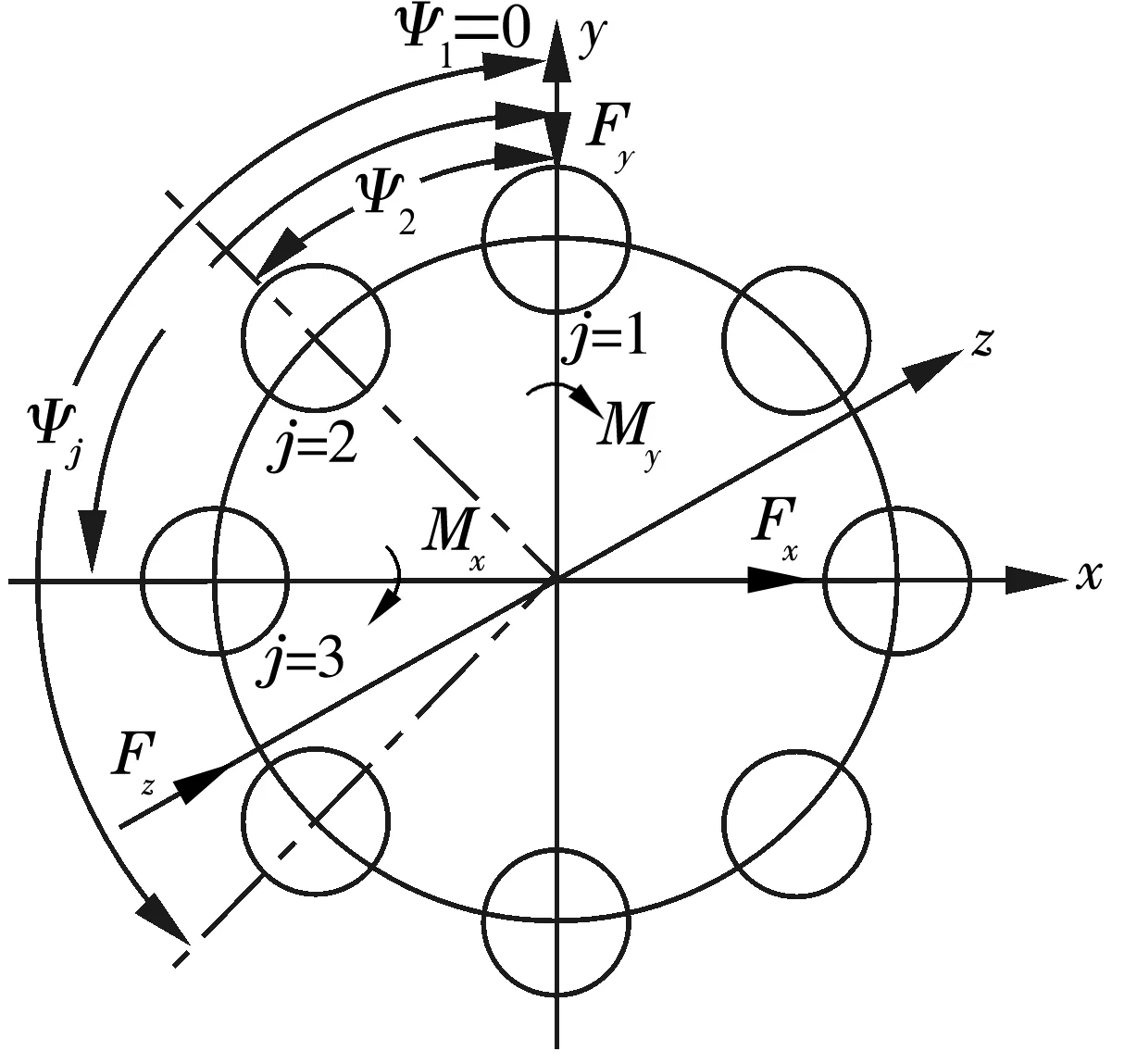
图1 轴承力学模型图

1.2 滚动轴承的受力分析

按照Hertz弹性接触理论，两物体在接触区的弹性趋近量与载荷满足[8]

Q=kδ1.5，

(1)

式中：k为Hertz接触常数，由材料的参数和接触物体的几何尺寸决定；δ为弹性变形量。

通过回归法得出点接触下的中心油膜厚度经验公式，同样适用于球轴承套圈与球之间油膜厚度的计算[9-10]，即

h=2.69RxV′69/100G′53/100W′-67/1 000×

(1-0.061e-73c/100)，

(2)

式中：Rx为接触物体在x平面的等效曲率半径；V′为归一化速度参数；G′为材料系数；W′为归一化载荷系数；c为Hertz接触椭圆长轴与短轴的比值。

角接触球轴承在高速旋转时，内圈在高速下产生较大离心力，因此产生的径向膨胀变形为[11]

(3)

式中：Ri，Re分别为轴承内、外圈半径；ρ为材料密度；ν为泊松比；E为弹性模量；ω为内圈旋转角速度。

接触变形发生在球与内、外圈沟道的接触处，当轴承受载并达到平衡后，内圈和球分别运动到新的位置，局部坐标系中轴承的受力如图2所示。图中l为内、外圈沟曲率中心之间的距离；A1j，A2j分别为内、外圈沟曲率中心的轴向、径向距离；αij，αej分别为内、外圈接触角；Lij，Lej分别为球中心与内、外圈沟曲率中心的距离。

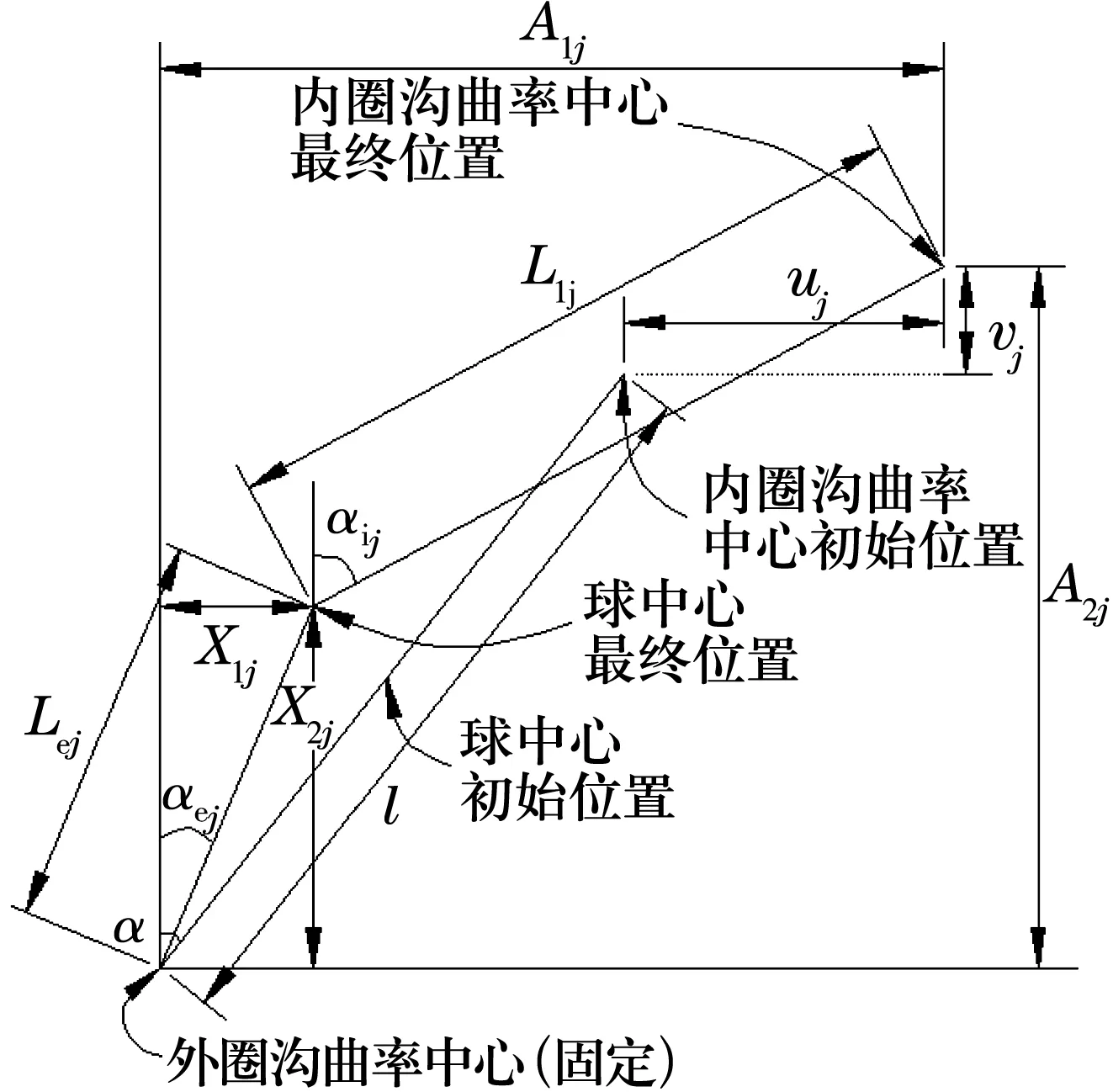
图2 球中心与沟曲率中心的位置

(4)

A2j=lcosα+δrcosΨj+εir+μir-εer,

(5)

式中：α为载荷作用前的初始接触角；δa，δr和θ分别为内外圈相对轴向位移、径向位移和角位移；dm为轴承平均直径；fi为内圈沟曲率半径系数；Dw为球径；εir和εer分别为内、外圈的径向热膨胀变形，可由有限元热分析得出[12]。

(6)

Lij=(fi-0.5)Dw+δij-hij，

Lej=(fe-0.5)Dw+δej-hej，

式中：hij，hej分别为内、外圈与钢球之间的油膜接触厚度；δij,δej分别为位置角Ψj时内、外圈的弹性变形。

高速角接触球轴承的球和内、外沟道的接触并非纯滚动接触，而是同时存在旋转和滑移。考虑到离心力和陀螺力矩作用，钢球的受力如图3所示。对于外圈沟道控制，可设系数λij=0且λej=2，否则设λij=λej=1[8]，这样可减小对精度计算的影响。

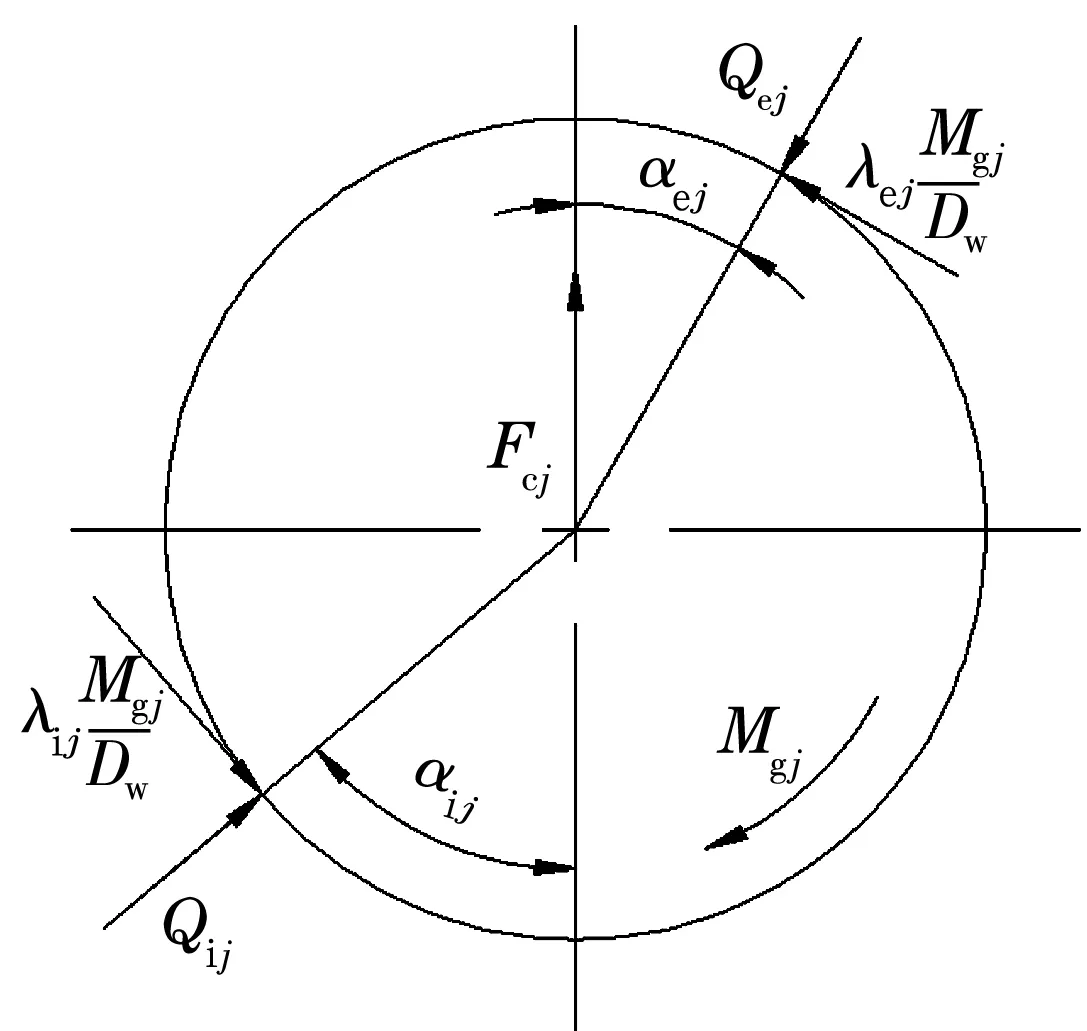
图3 位置角Ψj处钢球受力

考虑各力水平和竖直方向的平衡得

λijcosαij)，

(8)

式中：Fcj为离心力;Mgj为球受到的陀螺力矩;Qij,Qej分别为内、外圈接触力。

考虑整个轴承平衡条件，可得

2.16 请从邮局寄送单位推荐信及稿件审理费，推荐信应注明对稿件的审评意见、无一稿两投、不涉及保密、署名无争议等项。

(9)

r=0.5dm+(fi-0.5)Dwcosα0。

利用Newton-Raphson法对(1)～(9)式联立求解，可得到轴承载荷分布、接触角和陀螺力矩等参数。

1.3 弹流润滑牵引系数

对于运转的轴承，在载荷的作用下，球与内、外沟道之间存在点接触弹流润滑。由于接触区域较小，导致油膜压力很高。油在高压下向玻璃体转变，呈现出很强的非牛顿特性，即黏度与剪切率呈非线性变化，一般用黏-弹-塑性模型描述[13]。这种黏度的非线性变化导致了油膜的牵引系数也呈非线性。通过试验和理论分析，得到描述油膜牵引系数的经验公式为[12]

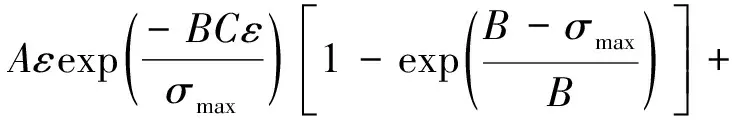
G[1-exp(-Cε)],

(10)

式中：ε为滑滚比；σmax为最大Hertz接触应力；A，B，C，G为经验系数。由此得到不同压力下，牵引系数随滑滚比的变化如图4所示。由图可知，初始时牵引系数随滑滚比的增加而变大，当达到一定数值后逐渐降低，且接触应力越大，牵引系数峰值越高。所以，对于球轴承，球在一定的接触应力状态下，其接触区所能提供的牵引力和抵抗沿陀螺枢轴滑动的阻力矩都是存在极限的。当陀螺力矩大于该阻力矩极限值时，就不可避免地发生滑动。

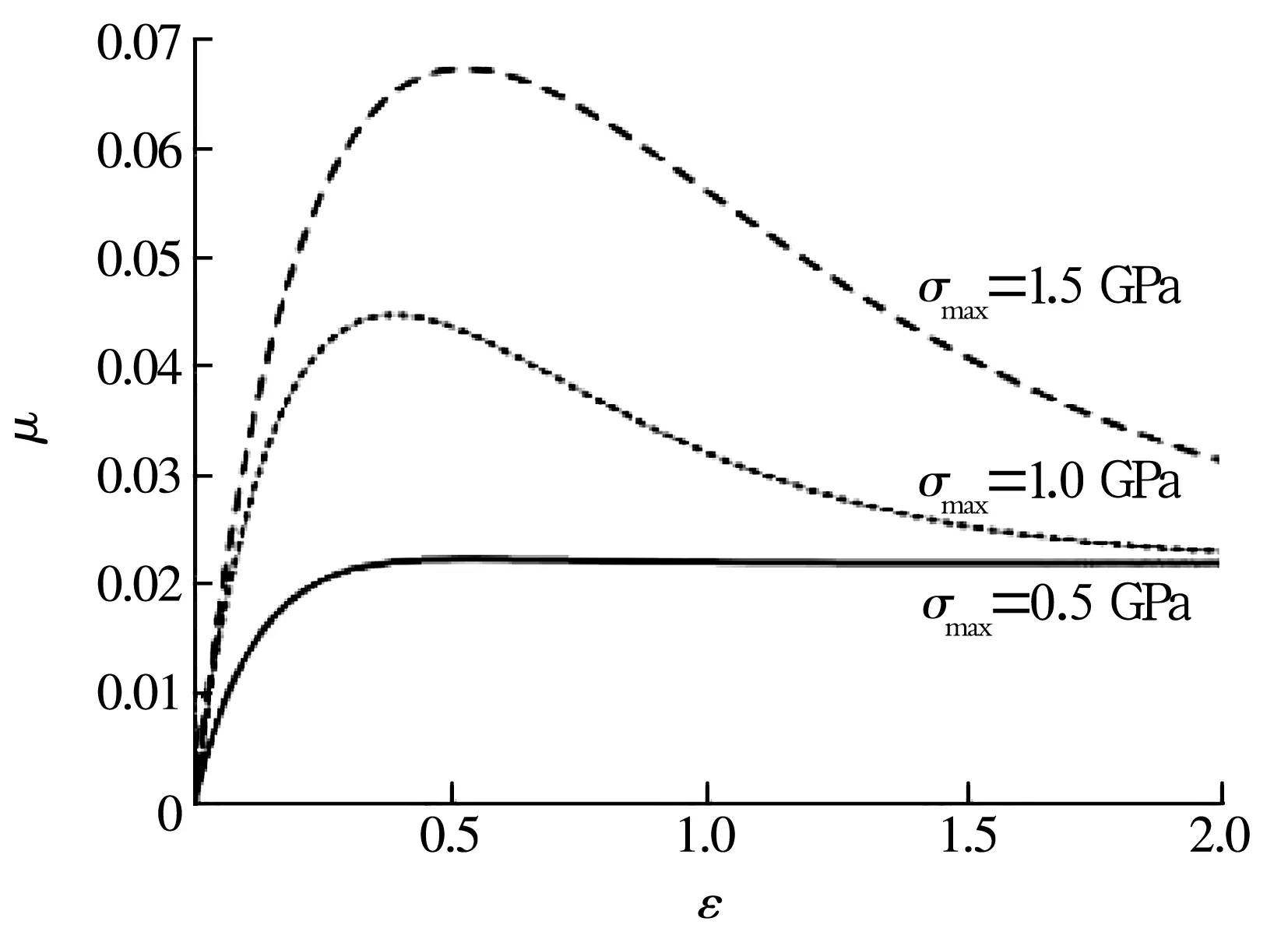
图4 牵引系数曲线

2 计算结果与分析

以7005角接触球轴承为例，其几何参数见表1。假设轴承不受径向载荷的作用，且轴向力Fa为1 kN时，通过对轴承力学模型的编程计算，得到球与外圈的最大Hertz接触应力为

σmax=0.007 33(n2dm)0.22(dmZη)-0.175，

(11)

式中：n为轴承转速；η为润滑油动力黏度，η=0.023 5 Pa·s。

计算结果与Boness[14]的经验公式(11)式的对比结果如图5所示。由图可知，随着转速的提高，陀螺力矩作用愈加明显，同时由于离心力作用使高速时外圈接触应力逐渐变大，最后趋于平稳。文中计算结果比经验公式的稍大，这是由于后者忽略了高速时内、外圈接触角的变化以及长时间运转引起轴承温升的影响，计算值与经典模型值的趋势相似、误差值较小，从而间接说明所建立分析模型的正确性。

表1 7005轴承计算参数

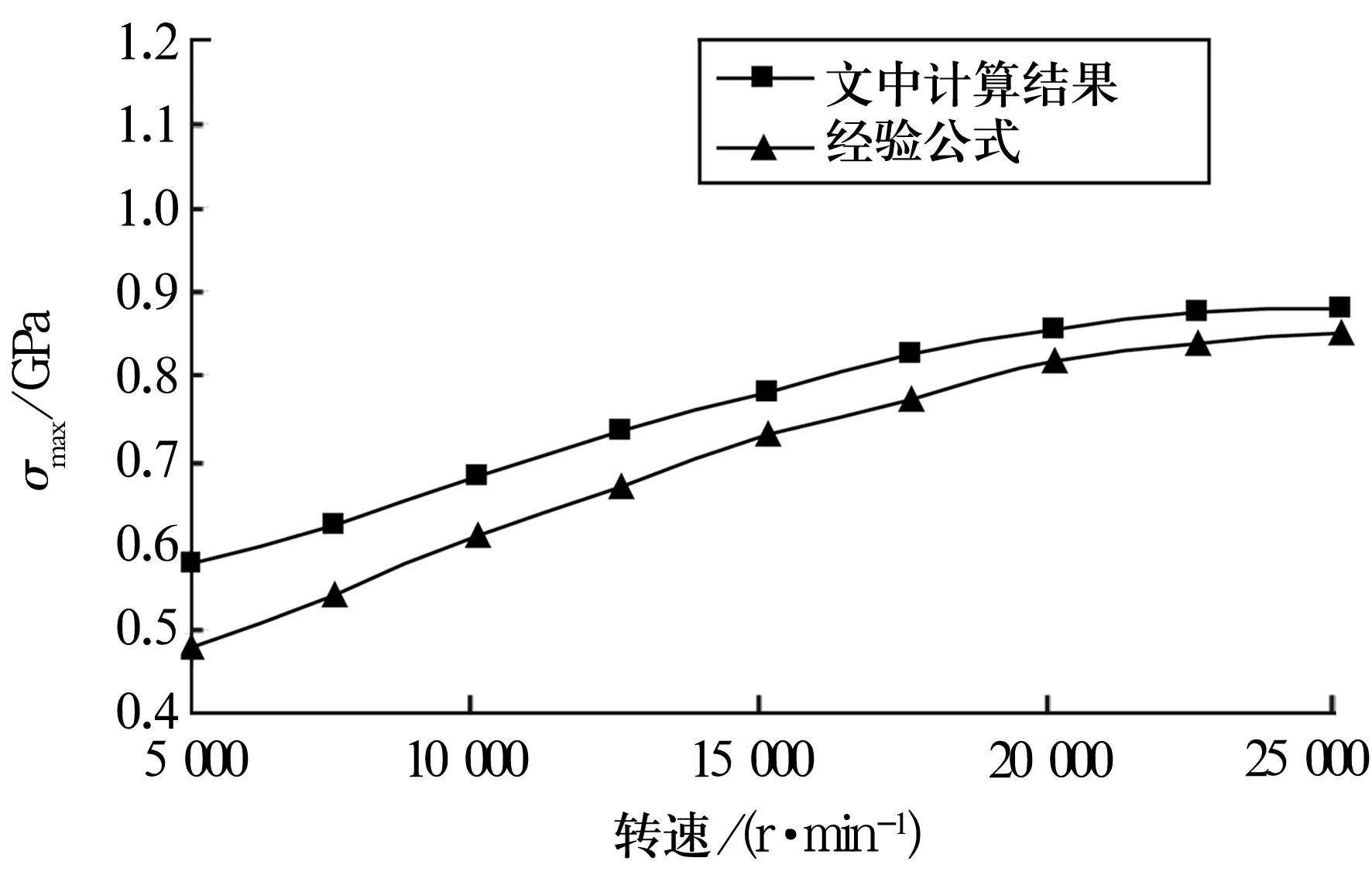
图5 外圈最大接触应力计算结果对比

轴承仅承受轴向力时球受力均匀，当轴承受径向力作用且轴向力不变(Fa=1 kN)时，轴承的受载区发生变化。球周向陀螺力矩和球与内、外圈接触载荷的变化分别如图6和图7所示。

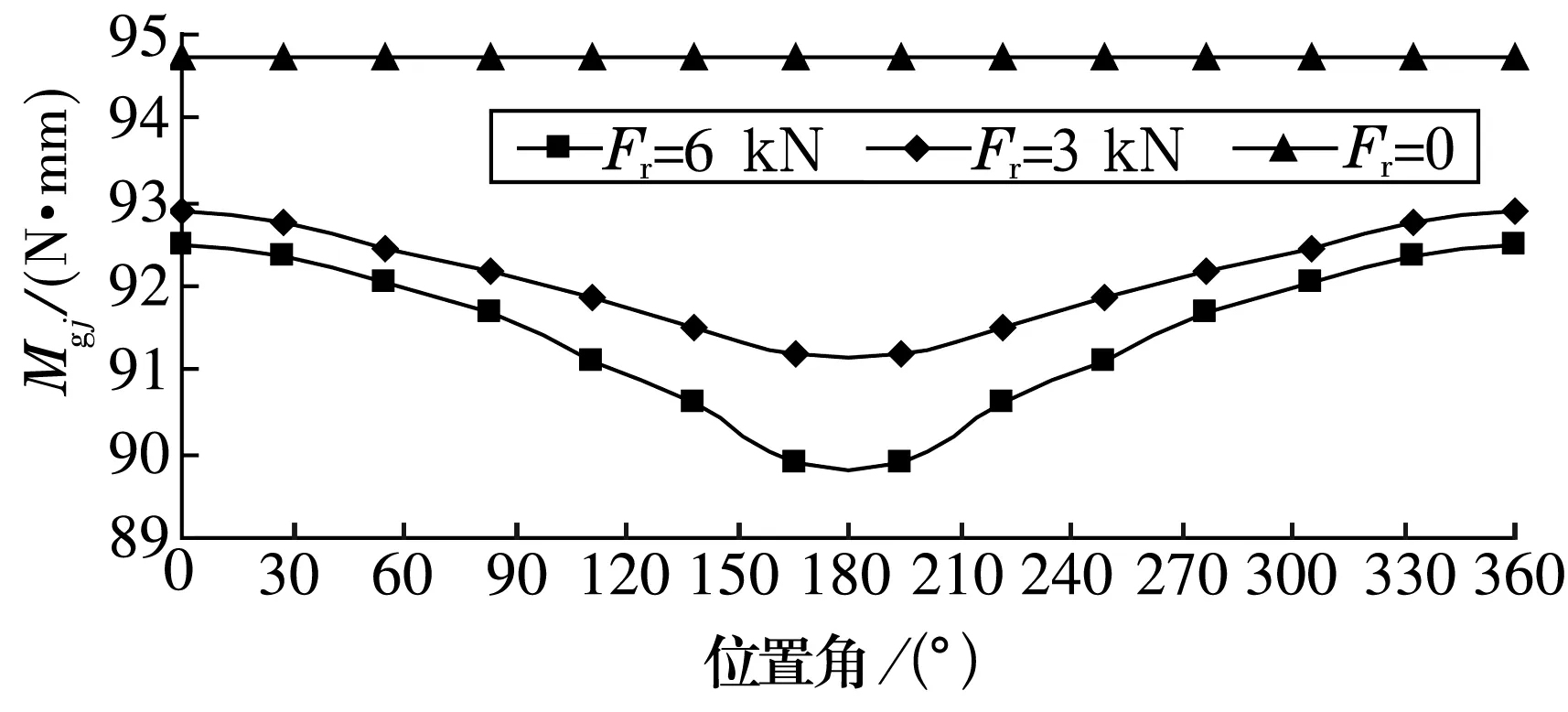
图6 球陀螺力矩

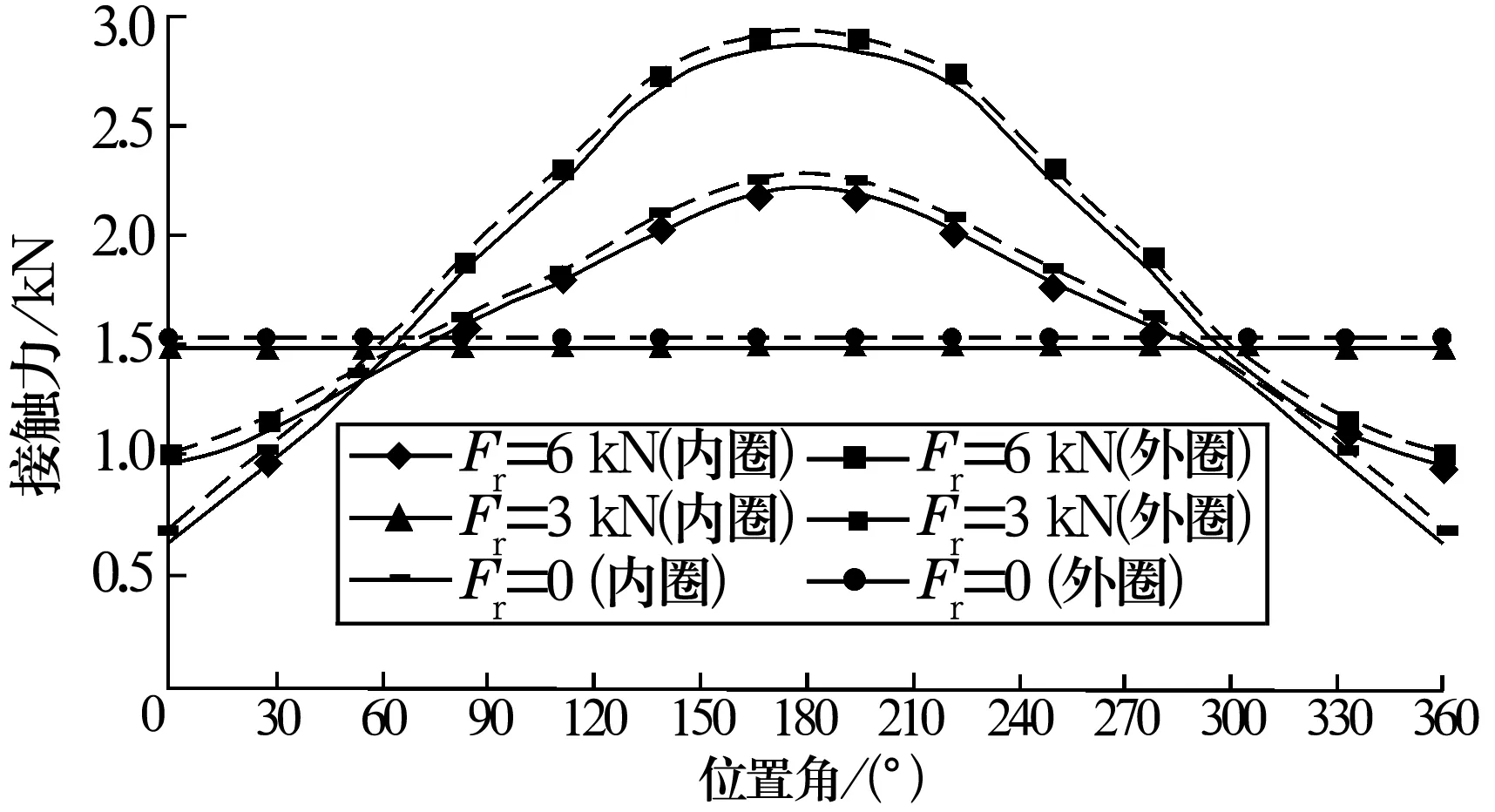
图7 内、外圈接触载荷

由图可知，随着位置角和径向载荷的变化，陀螺力矩发生规律性变化。位置角为180°的球承受的接触载荷最大，陀螺力矩最小。在摩擦力一定的情况下，为了减少发热和磨损，就要防止球与内、外沟道产生相对滑动。

摩擦因数一般取决于两接触物体的材料和表面粗糙度。不同的工况下，滚动轴承的工作温度、润滑条件及受力状况差异很大。高速转动的轴承在离心力的作用下球有向外运动的趋势，使其与内圈的接触角大于与外圈的接触角；同时在径向力的作用下，接触载荷发生变化，油膜的厚度也随之改变，从而影响摩擦因数。在不同位置角下摩擦因数的变化如图8所示。由图可知，摩擦因数不是一个定值，而是在0.04～0.12之间变化，随着轴承载荷的增加，摩擦因数也逐渐变大。

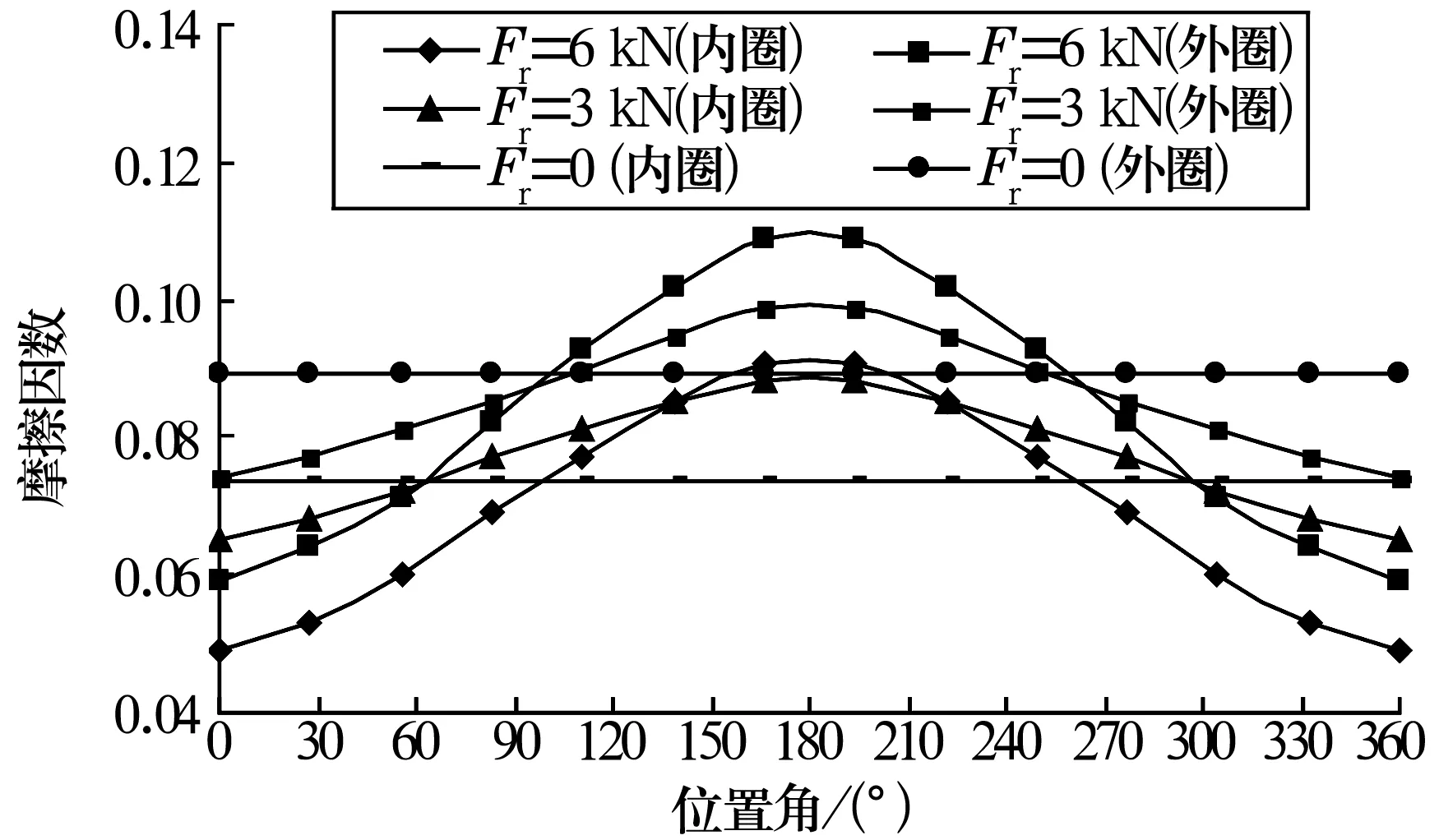
图8 内、外圈摩擦因数

轴承在高速旋转时产生很大的离心力，会使其产生离心力膨胀。为了研究离心力膨胀对轴承特性的影响，研究考虑和不考虑内圈离心膨胀效应时轴承的内、外圈接触角和接触载荷随转速的变化规律，分别如图9和图10所示。

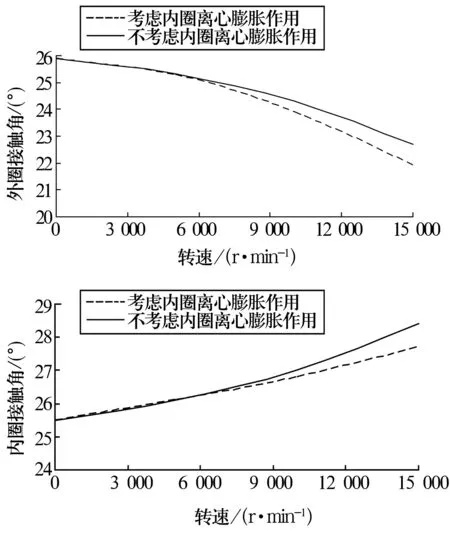
图9 接触角随转速的变化

由图9可知，在离心力的作用下球有向外运动的趋势，使其与外圈的接触角变小，与内圈的接触角变大。转速越高，离心力越大，接触角变化越明显。考虑内圈离心膨胀作用时，外圈接触角随转速升高的减小量增大；内圈接触角随转速升高的增大量减小。

由图10可知，随着轴承转速的提高，外圈接触载荷变大，内圈的接触载荷变小。考虑轴承离心膨胀作用时，外圈接触载荷变化量比不考虑时的要大，而内圈则呈相反变化趋势。

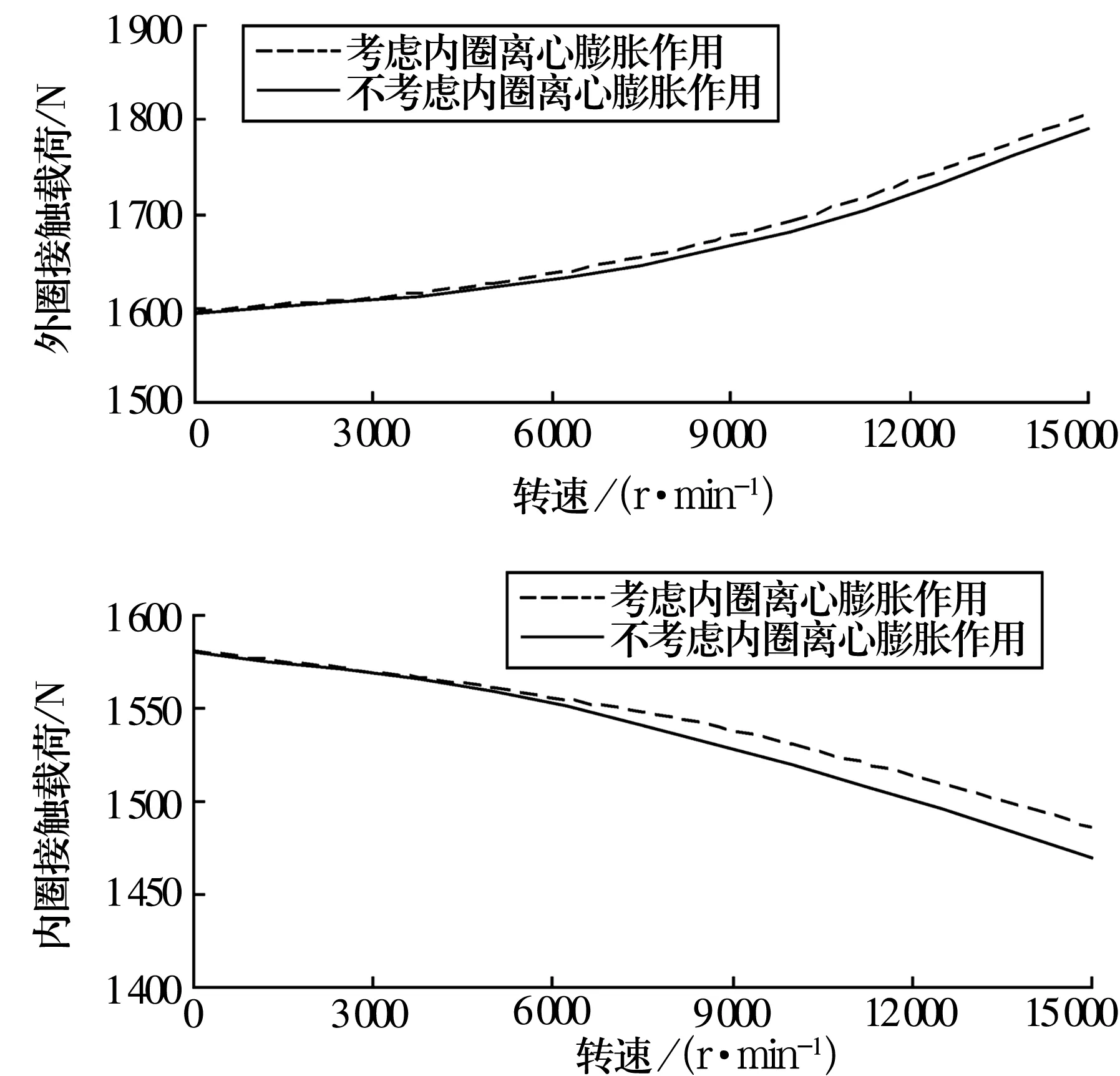
图10 接触载荷随转速的变化

3 结论

(1)建立了考虑转速、受力、润滑、摩擦及接触情况等影响因素的高速轴承力学模型，得到轴承接触角和接触载荷等参数。通过将建立的高速轴承力学模型与经验公式计算结果进行对比，间接证明了模型的正确性。

(2)随着位置角和径向载荷的变化，陀螺力矩发生规律性变化，在180°位置角时钢球承受的接触载荷最大，陀螺力矩最小。

(3)分析了不同位置角下钢球与内、外圈的摩擦因数，其值在0.04～0.12之间变化，随着轴承载荷的增加，摩擦因数也逐渐变大。

(4)考虑离心膨胀作用时，外圈接触角及接触载荷随转速的变化量比不考虑时的大；对于内圈，则结果相反。