一类wishart矩阵相对特征值的分布问题研究

卫 飚

(南京政治学院 基础部,江苏 南京 210003)

一类wishart矩阵相对特征值的分布问题研究

卫 飚

(南京政治学院 基础部,江苏 南京 210003)

在统计分析中，特征值的分布问题是重要内容。从wishart矩阵的密度函数得到AB-1特征值以及在r≤m条件下AB-1特征值的密度函数。

wishart矩阵;特征值;密度函数

在多元统计中经常遇到特征值的分布问题,若A～Wm(n,∑),n≥m,则A的密度函数为

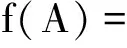
A的密度函数就成了A的特征值的函数,其次,在主成分分析、典型相关分析和不变检验中都要遇到求AB-1的特征值分布问题,因此特征值的分布问题是多元分布理论中的重要内容。

1 AB-1的特征值分布

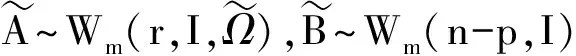
引理2[1]设A是一个m×m随机正定矩阵，其密度为f(A)，则A的特征值l1,…,lm的联合密度为

其中H∈O(m)，满足A=HLH′，而L=diag(l1,…,lm)，且L与H独立。

引理3[1]设X是一个m×m正定矩阵，Y是一个m×m对称矩阵，则

其中(dH)表示O(m)上的标准化不变测度。

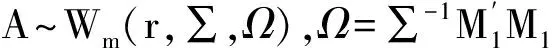
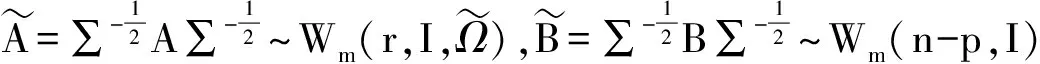
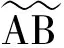
diag(f1,…,fm),H∈O(m)

(1)

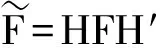
O(m)。所以有

由引理3

(2)

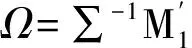
综上由(1)和(2)即得AB-1的特征值f1,…,fm的联合密度。

注：若M1=0，则Ω=0，此时AB-1的特征值f1,…,fm的联合密度为

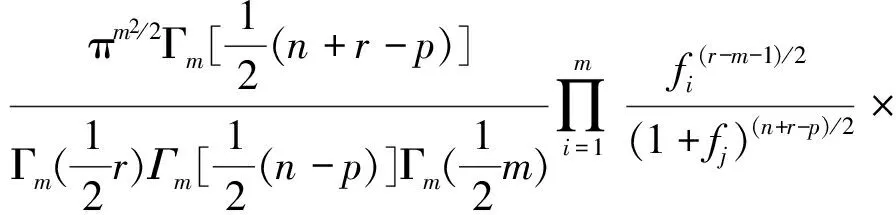
f1>f2>…>fm>0

2 r≤m条件下AB-1的特征值的密度函数

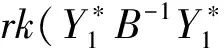
引理4[2]设A～Wm(n,∑)，n>m-1，M是k×m阶矩阵，rk(M)=k，则

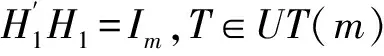
引理6[1]设Z是一个m×m复对称矩阵，Re(Z)>0，Y是一个m×m对称矩阵，则

且有

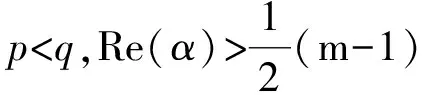
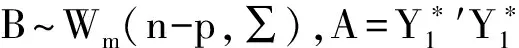
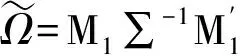
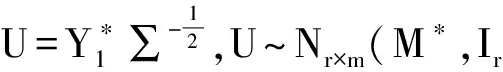
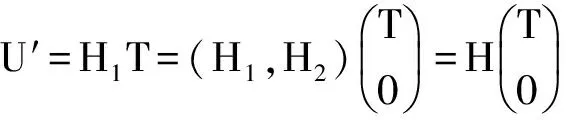
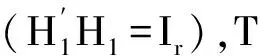
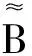
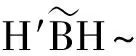
Wm(n-p,Im)

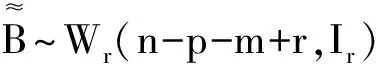
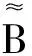
由于U′=H1T，其中H1∈Vm,r，这里Vm,r表示所有m×r列正交矩阵组成的Stiefel流形，根据引理5我们有

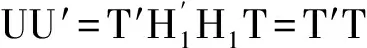
所以

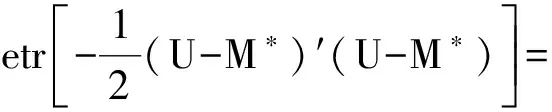
于是上述联合密度变为

现在对上式关于H1∈Vm,r积分

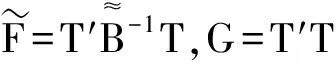
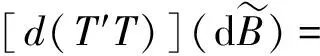
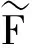
对该密度函数中关于G的因子积分

(3)

因为

由引理6 ，(3)式中有关因子的积分为

.

[1] 刘金山.Wishart分布引论[M].北京：科学出版社，2005.

[2] 朱道元，吴诚鸥，秦伟良.多元统计分析与软件SAS[M].南京：东南大学出版社，1999.

(责任编辑：张英健)

StudyontheDistributionProblemofaClassofWishartMatrixEigenvalue

WEI Biao

(Department of Mathematics, Southeast University, Nanjing Jiangsu 210003, China)

In the statistical analysis,the distribution of eigenvalue problem is an important content of the characteristics of the density function obtained from the density function of the Wishart matrix and eigenvalue in the conditions ofvalue.

wishart matrix; characteristic value; density function

2014-07-10

卫飚(1977-),男,江苏无锡人,讲师,硕士,主要研究方向为概率统计。

O211.4

A

1671-5322(2014)04-0021-04