基于动态故障树的盾构刀盘失效风险分析
吴贤国, 张青英, 张立茂, 曾铁梅, 仲景冰
(1. 华中科技大学 土木工程与力学学院, 湖北 武汉 430074;2. 武汉地铁集团有限公司, 湖北 武汉 430030)
基于动态故障树的盾构刀盘失效风险分析
吴贤国1, 张青英1, 张立茂1, 曾铁梅2, 仲景冰1
(1. 华中科技大学 土木工程与力学学院, 湖北 武汉 430074;2. 武汉地铁集团有限公司, 湖北 武汉 430030)
地铁隧道施工是一个动态过程,针对在地铁隧道施工过程中经常发生的盾构刀盘失效风险分析宜采用动态评价方法。为了获得盾构刀盘失效的可能性并找到刀盘失效的关键致险因素,本文结合地铁隧道施工过程,建立动态故障树评价模型。然后将评价模型模块化成静态子树和动态子树以简化计算过程,并采用贝叶斯和离散贝叶斯分别对它们进行分析;在此基础上,预测出盾构刀盘在不同时段失效的可能性,并进行敏感性分析确定关键影响因素;最后通过工程实例验证了动态故障树在盾构刀盘失效风险分析中的实用性。
盾构刀盘失效; 动态故障树; 贝叶斯网络; 失效分析; 敏感性分析
在地铁隧道施工过程中,盾构机是不可缺少的挖掘工具,已被广泛应用于地铁隧道施工。盾构刀盘是盾构机的开路先锋,极易出现故障,有效评估盾构刀盘失效的风险、找到刀盘失效的主要影响因素有助于地铁隧道施工的顺利进行。
目前在进行工程安全风险分析时,通常采用的方法有事故树分析法、安全检查表法、预先危险性分析法等静态评价方法,但是这些方法无法描述系统失效的动态行为。相对而言,动态故障树将风险分析扩大到动态系统性能,具有顺序相关、时序性等特性,并且目前在系统可靠性及安全评价中已经得到广泛应用[1]。地铁隧道施工是持续的动态系统过程,很多工序、技术具有时序性,危险源和危险程度处于动态变化之中,面临的风险事件随着时间的推移不断变化。因而,对盾构刀盘失效进行风险分析时,采用动态安全评价方法更为适宜。
本文结合动态故障树分析理论,通过致险机理分析,找到导致盾构刀盘失效的影响因素,建立动态故障树评价模型,并采用离散贝叶斯和贝叶斯分析方法对盾构刀盘失效风险进行评估,结合敏感性分析找出盾构刀盘失效的关键致险因素,并进行实例分析验证。
1 动态故障树及其风险分析方法
1.1 动态故障树
动态故障树反映的是含有动态逻辑门的故障树。其中,动态逻辑门可以表示基本事件之间动态、时序性的逻辑关系,具体包括优先与门、顺序相关门、功能触发门、热备件门、温备件门、冷备件门[2]。最常见的优先与门与顺序相关门等动态逻辑门的特性及构成如下:
(1)优先与门(PAND)体现了事件发生的时序性,由两个基本事件和一个输出事件构成,基本事件也可以用逻辑门的组合来表示(图1)。当两个基本事件都发生,且满足两个按从左至右的顺序发生时,输出事件才会发生。
(2)顺序相关门
顺序相关门包含若干个基本事件和一个输出事件,当且仅当这些基本事件按照从左至右的顺序全部发生时,输出事件才会发生[3]。图2所示为3个基本事件的顺序相关门。
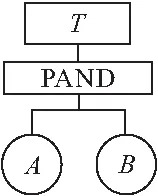
图1 优先与门
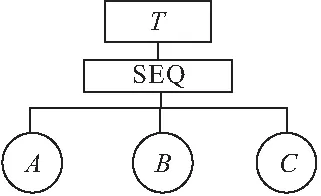
图2 顺序相关门
1.2 基于动态故障树的风险分析
动态故障树能够反映事件随时间变化的动态更新效应,适用于复杂环境下事件的风险分析。本文提出基于动态故障树的风险分析方法,具体包括以下四个步骤。
步骤1:动态故障树构建及模块化
动态故障树与传统故障树的区别在于增加了动态逻辑门,但二者的构建流程是完全相同的。动态故障树模型的构建流程为:(1)确定一个最不希望发生的事件作为顶事件;(2)由顶事件开始,逐级分析各级事件全部可能的直接原因,并用适当的动态逻辑门和静态逻辑门表示各级事件及事件间的逻辑关系,直至分析至底事件为止。构建动态故障树后,即可进行风险分析。动态逻辑门的处理过程较为复杂,不能采用传统故障树的处理办法来处理动态故障树。一般情况下动态故障树中只包含少量的动态逻辑门,所以首先可以根据动态门和静态门识别出动态故障树的动态子树和静态子树[4],使得每个独立子树的分析模型都很小,便于开展分析。
步骤2:静态子树分析
传统故障树的分析工具有二元决策图和贝叶斯网络等,其中,贝叶斯网络具备描述事件多态性和不确定性逻辑关系的能力。传统二态状态仅将节点分为失效和正常两种状态(分别用1和0描述),但在实际工程中,风险状态具有模糊性,本文采用语言值集合{严重失效,轻微失效,正常}来描述节点的失效状态,用{1, 0.5,0}表示,故应采用贝叶斯网络分析方法。贝叶斯网络包含两部分,一是由变量(节点)及连接它们的有向弧组成的有向无环图;二是条件概率表(CPT)。贝叶斯网络包含两类节点,没有导入箭头的节点叫做根节点,被箭头指向的节点叫做子节点,而其中箭头的来源节点叫做父节点。贝叶斯网络和离散贝叶斯都满足条件独立性假设:即在给定Vi的父节点pa(Vi)的条件下,Vi与非后代节点A(Vi)独立,即P(Vi|pa(Vi),A(Vi))=P(Vi|pa(Vi))。由贝叶斯网络的条件独立性假设可知,条件概率分布可以用P(Vi,pa(Vi))来描述,它表达了子节点与其父节点的定量关联关系[3]。确定静态子树后,根据对应规则将静态子树转化为贝叶斯网络来进行分析,对应规则在文献[5]中有详细介绍,本文不再赘述。采用传统贝叶斯来分析静态子树的流程为:获取根节点先验概率分布;给出子节点的条件概率表;风险预测。
(1)获取根节点先验概率。由于缺少精确统计数据,通过专家评分法来获取根节点的失效率λx,进而计算根节点先验概率分布。对于根节点x,其概率分布见式(1)和式(2),其中,x=[(zx-1)Δ,zxΔ)表示X在[(zx-1)Δ,zxΔ)区间内失效,本文令Δ=100(台班),便可以算出顶事件在每Δ台班内发生不同程度故障的概率;x=[T, ∞)表示x在任务时间T内未发生失效;λx为x的失效率,Δ表示时间间隔。在动态故障树分析中,一般均假设底事件服从指数分布,即失效率为常数,本文仍然沿用这一假设[6]。
P(x=[(z-1)Δ,zΔ))=e-λxzΔ(eλxΔ-1)
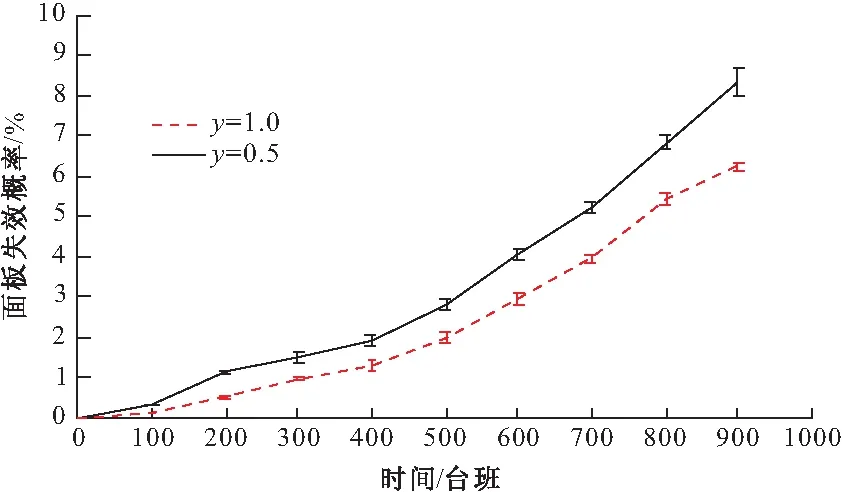
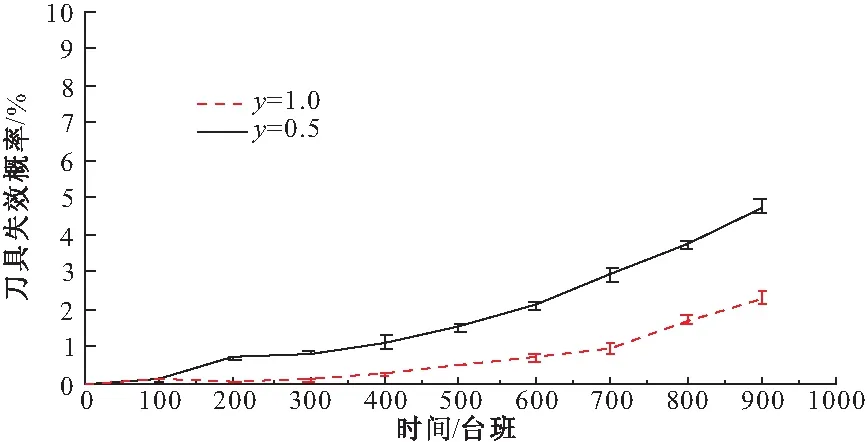
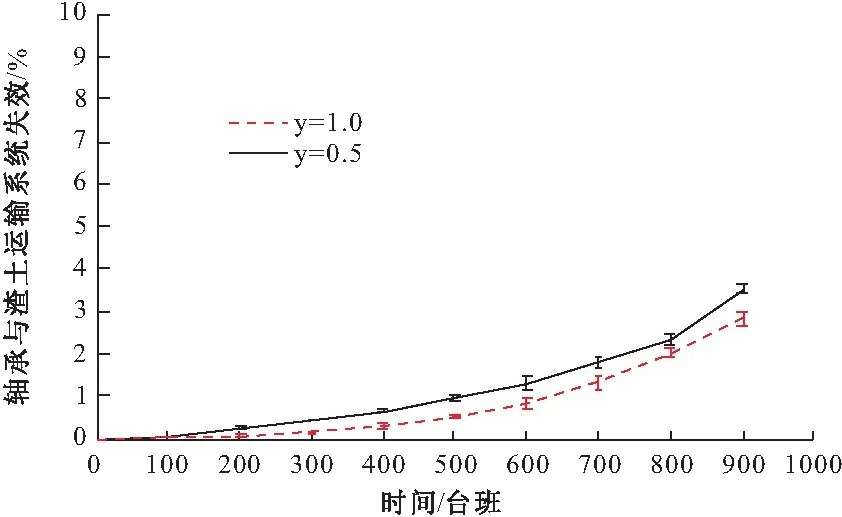
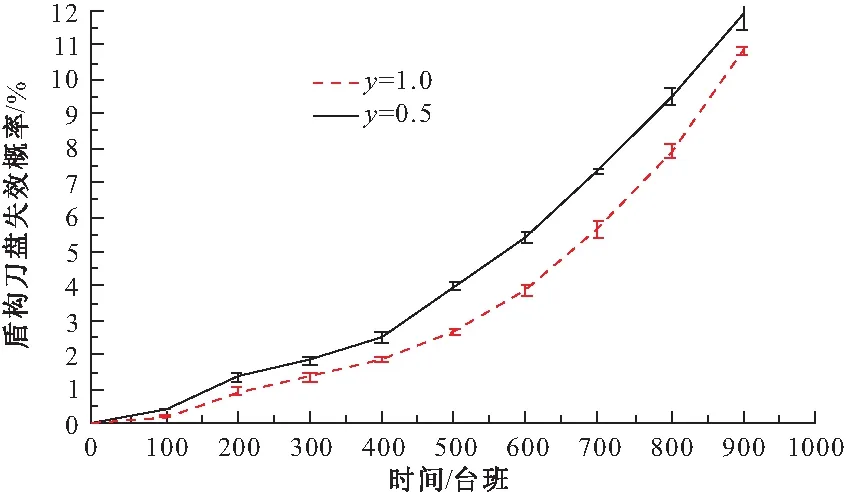
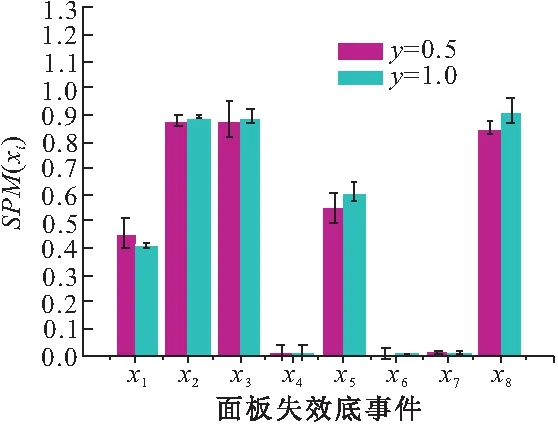
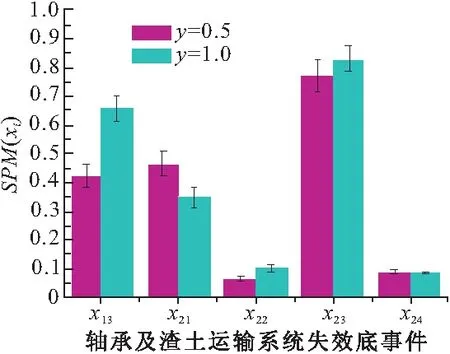
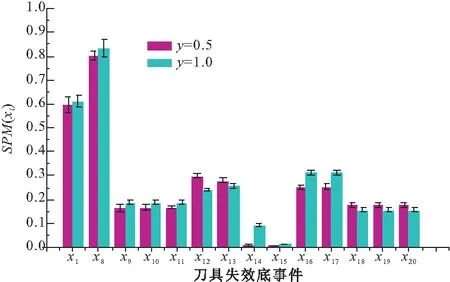
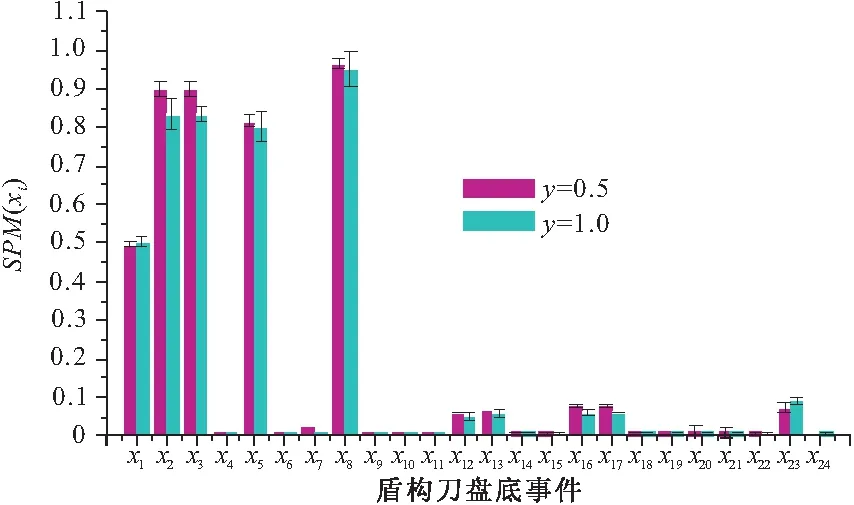
(0 (1) (2) (2)确定条件概率表。贝叶斯网络条件概率表(CPT)由事故树中逻辑门的逻辑关系映射而来。事故树逻辑门在表示节点间关系的时候只能表示确定关系,贝叶斯可以通过改变子节点的CPT赋值来表达节点间逻辑关系的不确定性和概率性[7]。本文在充分考虑专家知识以及工程实际的基础上,重新构建盾构刀盘失效贝叶斯网络条件概率表。 (3)风险预测。若已知一定的风险因素状态,就可以计算风险事件发生的条件概率,即风险预测。风险预测计算见式(3),其中,n表示状态已知的节点个数;若已知根节点各状态下的失效率,则叶节点T处于Tq状态下的概率用式(3)计算。P(T=Tq,X1=x1,X2=x2,…,Xn=xn), 表示所有失效率已知的底事件与风险事件同时发生的联合概率;失效率已知底事件的联合概率用P(X1=x1,X2=x2,…,Xn=xn)表示,它们都可以通过使用高阶联合概率计算低阶概率的方法获得。 P(T=Tq|X1=x1,X2=x2,…,Xn=xn) xi∈{0,0.5,1} (3) 步骤3:动态子树分析 动态子树通常采用梯形公式、离散贝叶斯网络(DTBN)和Markov链进行分析,梯形公式计算精度低,Markov链存在组合爆炸问题,DTBN可以克服二者的缺点,本文选择DTBN来进行动态子树的分析。具有N个节点的DTBN可用N=< (1)动态逻辑门向DTBN的转化。动态逻辑门向DTBN转化的规则和静态子树向贝叶斯转化的规则是相同的,区别在于要加上对应逻辑门符号表示时序关系。优先与门对应的DTBN如图3所示,顺序相关门及对应的DTBN如图4所示。 图3 优先与门DTBN 图4 顺序相关门DTBN (2)确定条件概率分布。节点的先验概率分布采用专家评分法获取,随后即可确定子节点的条件概率分布。优先与门顶事件Y的条件概率分布式为式(4)~(6),需要特别指出的是:如果节点A、节点B同时出现(是指两事件在同一个时间序列发生),认为优先与门的输出事件发生。在顺序相关门中,节点B和节点C的条件概率分布是相同的,以节点B为例来表示,见式(7)~(9),节点Y的条件概率分布见式(10)和(11)。 (3)风险预测。若顶事件ET在任务时间T内发生,则ET的发生时刻必定在[0,Δ), [Δ,2Δ), …, [(n-1)Δ,nΔ)中的一个区间之内,因而ET在任务时间T内的发生概率采用式(12)来计算,而P(ET=[(x-1)Δ,xΔ))可以通过联合概率分布直接计算,见式(13),式中:事件Ei(1≤i≤M-1)对应于DTBN中的非叶节点(即动态故障树中的中间事件和底事件);M为节点数目;ei∈{[0,Δ), [Δ,2Δ), …, [(n-1)Δ,nΔ), [T,∞)}用来表征Ei的发生区间。由式(12)和式(13)可以得到ET在任务时间T内的发生概率,见式(14)。 Pza,zb,zy=P(Y=[(zy-1)Δ,zyΔ)|A= [(zz-1)Δ,zaΔ),B=[(zb-1)Δ,zbΔ))= (4) Pza,∞,∞=(Y=[T,∞)|A=[(za-1)Δ,zaΔ),B=[T,∞))=1 (5) P∞,∞,∞=(Y=[T,∞)|A=[T,∞),B=[T,∞))=1 (6) Pza,zb=P(B=[(zb-1)Δ,zbΔ)|A=[(za-1)Δ,zaΔ))= (7) (8) P∞,∞=P(B=[T,∞)|A=[T,∞))=1 (9) Pzb,zb=P(Y=[(zb-1)Δ,zbΔ)|B=[(zb-1)Δ,zbΔ))=1 (10) P∞,∞=P(Y=[T,∞)|B=[T,∞))=1 (11) (12) (13) (14) 步骤4:敏感性分析 敏感性分析的目的是为了找到对顶事件发生影响较大的一些因素。本文提出一种敏感性指标(SPM,Sensitivity Performance Measure),用于表征每个风险因素对风险事件的贡献[9]。当SPM(xi)越接近于1,xi越容易成为该风险事件的直接诱因。如给定个别根节点的实际观察值,根节点xi的敏感性指标SPM(xi)的计算公式如式(15)所示。式中,Tq表示具有P个状态的风险事件,一般取风险较大的状态作为研究对象,如T=0.5,1等;xi表示具有Qi个状态的致险因素Xi。 (15) 2.1 致险机理分析 刀盘参数配置以及外部环境都会影响刀盘的工作状态,盾构刀盘失效(T)包含面板失效(y7)、刀具失效(y8)、轴承及渣土运输系统失效(y9)三种情况,这三个方面不存在时序的逻辑关系,可以构建图5所示的传统故障树。 图5 盾构刀盘失效静态子树 (1)面板失效在地铁盾构施工过程中很常见。地层软及粘性大(x2),软硬相间岩层(x3)、渣量体积大(x4)、地下异物及不良地质(x5)等外部因素,以及边缘滚刀配置不合理(x6)、刀盘选型不合理(x1)等刀盘自身因素均有可能导致面板失效。在遇到上述几种不良情况时,若是采取适当的施工管理措施(x7),改善盾构刀盘面板的工作环境或者更改刀盘配置,均可降低盾构刀盘面板失效的风险;反之,若是施工管理不当,则易使面板磨损量大(x8),从而失效[10]。从上面的分析可知,这些因素之间的时序逻辑关系可以用优先与门和顺序相关门表示,构建动态子树。 图6 面板失效动态子树 (2)刀具失效是刀盘失效的常见形式,地下异物及不良地质(x5)、滚刀装配扭矩过大(x9)、准备刀具不足(x10)、滚刀结构设置不合理(x11)、刀盘选型不合理(x1)、无降温装置(x12)、施工参数选择不合理(x13)、添加剂种类与用量不足(x14)、盾构姿态不断调整(x15)、推力偏大(x16)、刀盘工作压力偏大(x17)等因素有可能导致平刀圈磨损(x18)、刀圈断裂或崩角(x19)、刀鼓偏磨(x20),前面的影响因素出现故障时,才会形成刀具失效的状态[11]。显然,上述因素之间存在时序逻辑关系,应采用优先与门表示,构建动态子树。 图7 刀具失效动态子树 (3)轴承及渣土运输系统失效是盾构刀盘失效的组成部分,一般是由于施工参数不合理(x13)、泡沫注入孔数量偏少(x21)、阀片磨损(x22)、密封件失效(x23)、旋转接头更换时间长(x24)等因素引起[12],这些底事件之间不存在动态逻辑关系,用传统故障树表示(图8)。 图8 轴承与渣土运输系统失效静态子树 2.2 盾构刀盘失效动态故障树构建 从上文的致险机理分析可以看到,面板失效和刀具失效的底事件之间存在着先后发生的时序关系,此处采用顺序相关门和优先与门来表示底事件之间的逻辑关系;轴承与渣土运输系统失效的底事件之间的逻辑关系则可用静态逻辑门表示。由此构建图5所示盾构刀盘失效的动态故障树,显然,可将动态故障树模块化成图6和图7对应的动态子树和图8对应的静态子树。其中,y1、y2、y3、y4、y5分别代表刀盘配置不当、地质条件恶劣、刀盘配置导致面板失效、地质因素导致面板失效、刀具出现故障。显然,可将动态故障树模块化成如图6和图7对应的2个动态子树和图8对应的静态子树。 3.1 工程背景 武汉地铁2号线汉口火车站至范湖站右线隧道地层情况为:表层为松散的人工填土,上部为第四系全新统可塑状态的黏土,软~流塑质的淤泥质粉质黏土,淤泥质粉质黏土夹粉土,粉质黏土夹粉土、粉砂、细砂,区间隧道主要穿越(3-3)层淤泥质粉质黏土,(3-4)层淤泥质粉质黏土夹粉土、粉砂,(3-5)粉质黏土、粉土、粉砂互层,局部穿越(4-1)粉细砂。隧道结构埋深约为9.6~13.3m,隧道结构顶板位于(3-3)淤泥质粉质黏土层,隧道结构底板位于(3-5)粉质黏土、粉土、粉砂互层,地层地质情况如表1所示。汉范站选用的盾构机为德国海瑞克s438土压平衡式盾构机,最大直径为Ф6280。由于在武汉的地质特性中,汉口和武昌的差异很大,汉口地区主要是土砂性质地层,而武昌地区多是岩石地层,盾构机必须同时兼顾汉口和武昌地层的要求,所以采用的是面板式的刀盘,设计为可以全盘安装滚刀的型式,开口率为32%。 表1 地层地质情况 3.2 风险分析 在工程相关地质资料和盾构机型号已知的情况下,即可获取底事件失效率,再根据前文所建动态故障树,结合贝叶斯和离散贝叶斯理论分别获取事件的条件概率表和条件概率分布,计算顶事件发生概率,进行风险预测。本文以“地铁及地下工程风险管理指南”为依据来设定概率值与风险发生可能性的对应关系,确定当风险概率大于10%时,事故会频繁发生。 (1)先验概率 结合工程地质资料和专家经验[12],可以得到底事件失效率(表2),根据式(1)、(2)求取先验概率。 表2 面板失效底事件失效率 (2)条件概率表和条件概率分布 同理,查阅文献并结合专家经验[12],可以获取贝叶斯的条件概率表和离散贝叶斯的条件概率分布。下面给出顶事件在[100, 200)(T=2,Δ=1)发生时文中顺序相关门(SEQ)的条件概率分布(表3)。 表3 条件概率分布 (3)计算顶事件发生概率 根据底事件先验概率和表(3)所示条件概率分布,可以算出[100, 200)台班内面板失效的概率。给出其他底事件的先验概率,同理可以得到刀具失效,轴承及渣土运输系统失效概率,盾构刀盘失效在T=[0,100),[100,200),[200,300),[300,400),[400,500)[500,600),[600,700),[700,800),[800,900)等时段内发生的概率,如图9~图12所示。 图9 面板失效趋势 图10 刀具失效趋势 图11 轴承及渣土运输系统失效趋势图 图12 盾构刀盘失效趋势 盾构机在工作过程中,由于部件的疲劳等原因,刀盘失效的概率会逐渐增加。结合上图分析,可以得到以下结论:随着工作时间的延长,面板失效,刀具失效,和盾构刀盘失效的概率同步增长,而处于安全状态的概率逐渐减少,并且严重失效的概率比轻微失效的概率增长要快;面板失效的可能性最大、其次是刀具失效、最后是轴承及渣土运输系统失效。另外,此盾构机的寿命为2300个台班,设当失效概率达到10%,也就是刀盘严重失效频繁发生时,如图12所示,在[800,900)时段内应该对刀盘进行大修,此分析结果与实际情况相符。 3.3 敏感性分析 根据根节点的敏感性指标大小,可以判断底事件对顶事件的影响程度,对指标大的影响因素重点关注,可以降低盾构刀盘失效的概率。本文针对的是作业环境和自身配置确定的盾构机,根据式(15),可以分析某个时段盾构刀盘面板底事件的敏感性,本文以[0,100)台班段为例来进行敏感性分析,各系统及盾构刀盘敏感性分析结果见图13~图16。 图13 面板失效敏感性分析 图14 轴承及渣土运输系统敏感性分析 图15 刀具失效敏感性分析 图16 刀盘失效敏感性分析 影响因素的SPM(xi)越大,对顶事件的影响越大。刀盘失效时,应该最先排查敏感性大的因素,SPM(xi)的大小排序可作为刀盘失效故障的排查参考依据,从上面的计算结果可以看到,无论盾构刀盘是处于轻微失效还是严重失效状态,磨损量大、地层较软及黏性大、软硬相间岩层、地层软及粘性大和软硬相间岩层、不良地质及地下异物的SPM(xi)最大,说明在[0,100)台班内,这几个因素最有可能导致该刀盘面板失效,即说明这5个因素对刀盘失效的贡献较大。 由于地层结构复杂等原因,盾构刀盘在挖掘过程中极容易出现故障。本文使用动态故障树来进行盾构刀盘失效分析,并得到了以下结论: (1)本文提出了一套完整的基于动态故障树的失效风险分析方法,包括动态故障树构建及模块化、静态子树分析、动态子树分析等步骤,以便进行风险预测;另外,对失效影响因素进行敏感性分析,辨识关键因子。 (2)利用动态故障树描述底事件间的时序逻辑关系,构建了盾构刀盘失效风险分析故障树,包含致险机理分析、构建动态故障树两个步骤,并在此基础上结合工程实例进行风险预测和敏感性分析。 (3)将动态故障树理论运用到盾构刀盘失效风险评估实例中,风险预测的结果表明,随着时间推移盾构刀盘轻微失效和严重失效的可能性增大,且后者增幅较快,面板失效导致刀盘失效的可能性更大;敏感性分析的结果表明,在[0,100)台班内,磨损量大、地层较软及黏性大、软硬相间岩层、地层软及粘性大和软硬相间岩层、不良地质及地下异物等是影响盾构刀盘失效的最重要的因素,需要重点监控与排查。所得结果与实际工况保持一致,验证了将动态故障树运用到盾构刀盘失效风险研究的实用性。 [1] 韦建平.动态安全评价方法在建设领域的应用设想[J] .中国安全生产科学技术,2006,2(6):94-97. [2] 武文斌,汪立新,周小刚.基于动态故障树的惯导系统安全性分析[J] .电光与控制,2011,18(9):98-101. [3] 张立茂,陈虹宇,吴贤国.基于贝叶斯网络的复杂工程安全管理决策支持方法研究[J].中国安全科学学报,2011,21(6):141-146. [4] 段凌浩,郭爱民,潘 勇. 动态故障树分析算法研究综述[J].电子产品可靠性与环境试验,2013,31(4):59-63. [5] 王广彦,马志军,胡其伟.基于贝叶斯网络的故障树分析[J].系统工程理论与实践,2004, (6):78~83. [6] Manno G,Chiacchio F,Pappalardo F.The dynamic-to-static conversion of dynamic fault trees using stochastic dependency graphs and stochastic activity networks[J]. Engineering,2013,5(2):157-166. [7] 张晓洁,赵海涛,苗 强,等.基于动态故障树的卫星系统可靠性分析[J].宇航学报,2009,30(3):1249-1254. [8] 谢 斌,张明珠,严于鲜.贝叶斯网络对故障树的改进[J].燕山大学学报,2004,28(1):55-58. [9] Portinale L,Ratieri D C,Montani S.Supporting reliability engineers in exploiting the power of dynamic bayesian networks[J]. International Journal of Approximate Reasoning,2009,51(2):179-195. [10]周忠宝,周经纶,孙 权,等.基于离散贝叶斯的动态故障树分析方法[J].西安交通大学学报,2007, 41(6):732-736. [11]蒙先君.复合式土压平衡盾构机刀盘常见故障(损坏)原因分析及解决措施[J].隧道建设,2004,24(2): 61-66. [12]黄宏伟,闫玉茹,胡群芳.复合式土压平衡盾构刀盘失效风险分析[J].岩土力学,2009,30(8):2324-2330. Safety Analysis for Shield Cutter Failure Based on Dynamic Fault Tree WUXian-guo1,ZHANGQing-ying1,ZHANGLi-mao1,ZENGTie-mei2,ZHONGJing-bing1 (1.School of Civil Engineering and Mechanics, Huazhong University of Science and Technology,Wuhan 430074, China; 2. Wuhan Metro Group Co Ltd, Wuhan 430030, China) Metro tunneling is a dynamic process, and it is suitable to adopt dynamic evaluation method to analyze shield cutter head failure risk in metro tunneling. In order to gain cutter head failure probability and key risk factors, this paper adopts Dynamic Fault Tree (DFT) to build risk decision model. Then the model is modularized into independent static sub-trees and dynamic sub-trees, Bayesian and Discrete Bayesian algorithm are applied to progress them respectively. On the basis, cutter head failure probability in different time is predicted. Sensitivity analysis is performed to decide key risk factors. At last, project case demonstrates the feasibility of the proposed method. shield cutter head failure; DFT; bayesian network; failure analysis; sensitivity analysis 2014-06-05 2014-09-02 吴贤国(1964-),女,湖北武汉人,教授,博士,研究方向为土木工程与施工管理(Email: wxg0220@126.com) 张立茂(1987-),男,湖北荆州人,博士,研究方向为工程安全管理(Email: wxg0220@126.com) 国家自然科学基金(51378235);武汉市建委科技项目(201208; 201334) U455.1 A 2095-0985(2014)04-0060-07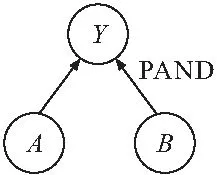

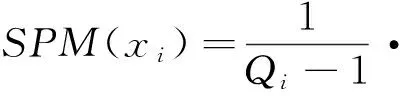
2 基于动态故障树的盾构刀盘失效风险分析
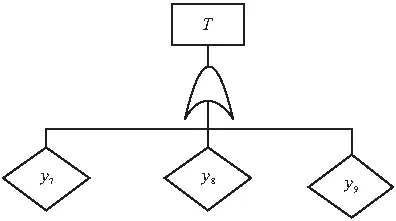
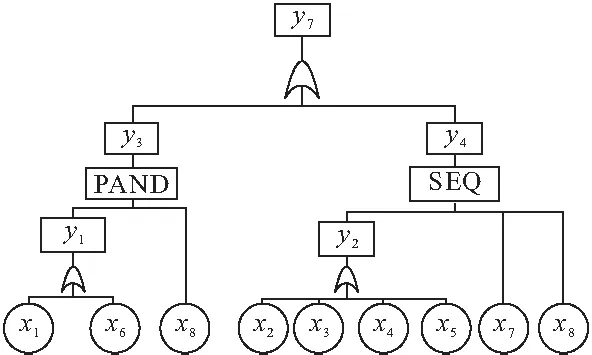
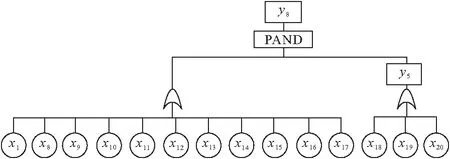
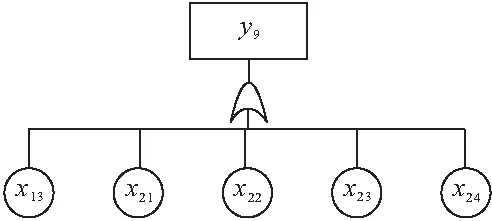
3 案例研究



4 结 论

