船舶直线航行控制技术综述

中国船级社 刘 超

直线航行是船舶运行的重要形式之一，对于降低船舶运营成本，提高船舶航行效率、缩短航行时间具有重要的意义。然而，在实际航行中，直线航行会受到诸多因素的限制。首先，船舶的航迹模型具有较强的非线性特性，传统闭环控制策略很难处理这一复杂的系统；其次，船舶航行系统为典型的欠驱动系统，即此类系统的控制变量比控制输入的数量多，进而增大了控制器设计的难度；第三，通常情况下，船舶的运行环境较为恶劣，易受到风浪等因素（如航行中会受到风流压差角）的影响，从而导致船舶实际航迹偏离期望的航行路线。因此，设计高性能的航行控制器，保证船舶的直线航行、节约船舶运营成本具有十分重要的意义。本文主要介绍船舶航行的非线性模型和航行控制器设计中常用的理论技术，为实际中船舶航行控制器设计提供有价值的参考依据。

船舶直线航行理论模型

实际中，船舶航行示意图和航迹示意图分别如图1和图2所示。

图1 实习船航行示意图

图2 船舶航迹示意图

图1显示，直线航行是船舶作业的重要形式，在实际应用中具有重要的价值。图2展示了船舶航行中的控制变量。图2中，x，y分别为船舶所在海洋坐标系XOY中的横纵坐标，U为船舶航行的实际速度（同时表示船舶的航行方向）；φ表示航向角，假设船舶期望的航行方向为X轴正方向，则φ表示船舶实际航行方向与X轴之间的夹角。

在理论分析中，通常采用Nomoto理论模型来表示船舶航行模型，其具体形式如下

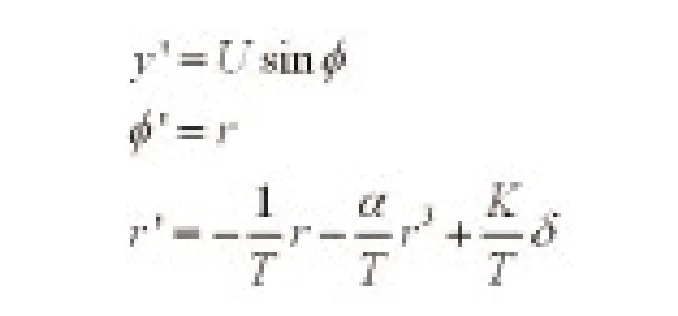
式中：r 为艏摇角角速度；δ 为控制输入，其物理意义为舵角；T,K,α 表示船舶控制系统参数。显然，Nomoto 模型为欠驱动模型，并且具有很强的非线性。

船舶直线航行控制器设计的目标就是通过设计舵角δ，使船舶在海洋坐标系XOY中，能够沿X轴保持直线行驶，即通过改变船舶舵角的输出，来调整船舶的运行方向，保持其直线航行。

船舶航行中的控制技术

近年来，针对模型中的强非线性、所受扰动的复杂性，很多先进的控制理念和控制技术应用到了这一领域中，并取得了较好的仿真和实验效果。下面对控制器设计通常采用的技术做详细的介绍。常用技术主要:

反馈线性化技术。由于非线性系统的复杂性，在理论分析和实际控制中，根据输出反馈或者状态反馈，通常将非线性系统等价地表示为线性系统，从而降低控制器设计的复杂性，这一技术称为反馈线性化技术。反馈线性化的核心目的是将原系统的状态方程转换为线性的、能控能观的状态方程。一般地，反馈线性化方法包括输入-状态反馈线性化、输入-输出反馈线性化、直接反馈线性化和逆系统方法等，其中前两者较为常用。对于，输入-状态反馈线性化，设计中要求系统中全部的状态变量是可测的，并且转换后的状态变量也是可测的。输入-输出反馈线性化，不需要系统状态变量是可测的，只需要输出可测且r阶可导，其中r为系统的相对阶数。

在实际船舶直线航行控制中，如果只考虑系统的镇定问题，可以采取输入-状态反馈线性化；如果考虑航迹的追踪问题（即追踪直线轨迹），则需要采用输入-输出反馈线性化，从而提高控制器设计的效率。

Backstepping技术。Backstepping技术是Kokotovic等人于1991年针对具有特定结构的非线性系统，提出的一种系统化的控制器设计方法。这一方法对于改善系统H2/H∞特性，保证系统稳定性，提高系统的追踪精度有良好的效果。这一方法已经在航空航天控制领域、船舶控制等领域得到了实际应用，并取得了较大的进展。一般情况下，Backstepping技术适用于具有“下三角结构”的系统模型中，而船舶航行欠驱动系统恰恰属于这类模型。

Bacstepping技术设计中的三要素为：“下三角”结构的系统模型、控制Lyapunov函数（CLF）和递归设计程序。设计流程为：首先，将原系统分解为子系统；其次，从第一个子系统开始（通常为控制系统输出），为使每一个子系统实现渐近稳定，选择对应的CLF，从而设计该子系统的虚拟控制输入；第三，根据上一个子系统的虚拟输入，做坐标变换，以误差信号为状态变量继续设计对应的虚拟输入；重复上述过程直到最后一个子系统，从而保证整个系统的稳定性或者收敛性。

在船舶的直线航行控制中，为降低算法的复杂性，减少运算量，通常会结合反馈线性化技术：首先，根据输入-输出反馈或输入-状态反馈，将Nomoto非线性模型转化为具有“下三角结构”的线性模型，而后应用Backstepping技术，使系统镇定，实现船舶的直线航行。

滑模控制技术。滑模控制理论是鲁棒变结构控制理论的主体，是针对非线性系统设计控制器的一种有效工具。滑模控制技术的核心思想为，根据系统的状态变量或者追踪误差，选择合适的滑模面。通过控制滑模面的动态特性和收敛特性，迫使系统按照预定的“滑模动态”的状态轨迹运行，实现渐近稳定或者渐近追踪。滑模控制技术具有响应快，对系统参数的鲁棒性较好，物理实现简单等优点。通常情况下，滑模面的动态收敛过程如图3所示。

图3 滑模面动态示意图

图3中，s=0表示滑模面动态，e为误差或者状态变量，e'为误差或者状态变量的导数。滑模面的选择对控制器的性能有很大的影响。通常滑模面的选择分为线性滑模面和非线性滑模面。线性滑模面通常选择为系统状态变量或者追踪误差的线性组合；而非线性滑模面在选择时有很大的空间，如二次切换线、连续二阶滑模、积分滑模等。

在实际船舶直线航行控制中，可以不通过反馈线性化的方法，直接对非线性系统设计动态滑模面，通过滑模面的收敛使船舶航行系统镇定（或追踪理想航行轨迹），从而有效提高系统响应的快速性，并降低系统对参数扰动的敏感程度。

神经网络控制技术。神经网络控制是智能控制技术的一种，属于现代数学的范畴，是处理非线性系统的一种有效工具。这一方法通过模仿生物神经网络行为，从而对非线性系统进行并行分布式控制。神经元网络系统的设计核心分为三个部分：神经元模型、神经网络结构、神经网络学习方法。从神经元模型的角度，神经元分为线性处理单元和非线性处理单元；从神经网络结构分析，可以分为前向网络、反馈网络和自组织网络，其中比较常用的有Hopfield网络、RNN网络；神经网络的学习方法分为有导师学习（相关学习、纠错学习等）和无导师学习。神经网络控制技术通过训练网络，来逼近模型中的非线性因素。因此，网络越复杂对非线性逼近越好，同时控制器的运算耗时也越大。

在船舶直线航行控制中，由于船舶航行模型具有较强的非线性，因此可以选择合适的人工神经网络（如Hopfield网络）逼近非线性模型，从而设计航行控制器。这种方法避免了使用反馈线性化技术，但是控制器的设计需要同时考虑模型的逼近误差和系统的实时性。

自适应控制技术。自适应控制是控制领域中非常重要的一种控制技术。由于被控对象中存在元器件的老化等因素，因此会导致模型中的参数不准确。自适应控制正是针对这类参数化的不确定提出的。一般地，自适应控制器设计方法分为频域和时域两种方法。频域方法主要针对线性系统，通常采用模型参考自适应控制；时域方法则可以同时处理线性和非线性系统，通常根据Lyapunov函数设计未知参数的自适应律。

在船舶控制技术中，为了处理模型中的参数化的不确定，一般会在控制器中同时引入自适应策略。例如，将自适应控制策略与Backstpping技术相结合，通过设计未知参数的Tuning Function，可以显著提高控制系统对未知参数的鲁棒性，提高船舶航直线行控制器的性能。

本文主要研究了船舶直线航行控制中常用的理论模型和相关自动控制技术。首先，介绍了船舶航行的非线性Nomoto模型。其次，针对Nomoto模型强非线性的特点，阐述了在控制器设计过程中通常采用的控制技术及其具体的实现方式和方法。文中重点描述了反馈线性化技术、Backstepping技术、滑模控制技术、神经网络控制技术和自适应技术的原理与设计流程，同时说明了各种方法的优缺点和相互结合的控制策略。因此，本文对船舶航行控制器的实际设计与应用具有一定的参考价值。相信在我国科研人员的更痛努力下，一定会克服一个又一个理论、实践难关，使我国屹立于世界船舶强国之列。