基于改进Elman神经网络的轴承故障诊断方法

涂俊翔，楼宇舟

(福州大学 机械工程及自动化学院，福州 350108)

轴承的故障诊断过程实质上就是一个模式识别过程，Elman神经网络以其独特的并行分布式处理、模糊匹配和良好的自学习等能力，在轴承故障诊断中得到了广泛应用[1-3]。但在实际工程中，由于数据规模较大，导致神经网络具有规模庞大、结构复杂、算法收敛速度慢及易陷入局部极小等问题，从而降低了其可靠性和实用性。

在此，采用基于信息熵的改进离散化算法对轴承故障数据进行预处理，去除一些不必要的属性样本信息，然后根据约简结果建立Elman神经网络系统进行故障诊断，可以克服单一神经网络规模庞大，收敛速度慢的缺点。

1 粗糙集理论

粗糙集理论是一种处理模糊和不确定性知识的数学工具，在决策分析、模式识别及数据挖掘等领域取得了很大的成功[4]。

1.1 知识与不可分辨关系

1.1.1 知识表达系统和决策系统

在粗糙集理论中[5]，定义一个信息系统为S=(U,A,V,f)。其中U={x1,x2,x3，…，xn}为一个非空的有限集合，称为论域；A为属性的非空变量集，A=C∪D，C∩D=，其中C为条件属性，D为决策属性；为属性值的集合，其中Va为属性a的值域；f:U×A→V为一个映射，对每个a∈A和x∈U定义了一个映射f(x,a)∈Va，即f指定U中的每一个对象x的属性值。

1.1.2 不可分辨关系

不可分辨关系是指由于缺乏一定的知识而不能将已知信息系统中的某些对象区别开的关系组，其实质是一个等价关系。

设S=(U,A,V,f)为一个信息系统，R为U上的一族等价关系，若P⊆R,且P≠，则∩P也是一个等价关系，称其为P上的一个不可分辨关系，用ind(P)来表示，即

ind(P)={(x,y)∈U×U:f(x,a)=f(y,a),a⊆P}。

1.2 粗糙集的上近似、下近似

当集合X为由基本等价类构成的并集时，则称集合X是R可精确定义的，称作R的精确集；否则，集合X是R不可精确定义的，称作R的粗糙集。集合的粗糙集可利用上近似和下近似2个精确集来描述。

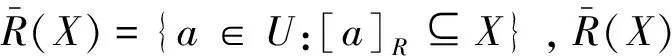
1.3 属性约简

属性约简是粗糙集理论的核心内容。在决策表中，往往具有很多不同的属性，而这些属性对于知识的决策具有不同的重要性，有些属性起决定性作用，有些属性则可有可无。在粗糙集理论中，在保持信息系统分类能力不变的情况下，通过消除冗余属性和冗余样本，最终得到信息系统的分类或者决策规则的方法称为知识约简。

设R为一个等价关系族，r∈R，如果ind(R)=ind(R-{r})，则称r是在R中不必要的，否则相反；若每个知识r都是等价关系族R中必要的，称R是独立的，否则称R是相关的。如果P=R-{r}是独立的，则P是R中的一个约简。

2 离散化算法和信息熵

2.1 离散化算法

由于粗糙集理论只能处理离散型数据，但在实际工程中获得的数据大多是连续的，实现属性值的离散化是应用粗糙集理论进行分析和处理的前提，因此可以将离散化算法视为整个机器学习过程中的数据预处理部分。离散化算法将连续值属性转化成有限个区间，并赋予每个区间1个离散值，从而完成离散化过程。合适的离散化算法不仅可以大大减少信息量，而且可以提高属性值分类的准确性[6]。

2.2 信息熵

信息熵是信息源不确定性的量度。每个信息源都有且只有1个信息熵，不同的信息源由于统计特征不同，所得的熵也不同。一个系统越有序，信息熵就越低；反之，系统越混乱，信息熵就越高。所以，信息熵也可以说是系统有序化程度的一个度量。Shannon把信息熵定义为随机离散事件的出现概率，即信息源的平均信息量[7]，表示为

(1)

式中:pi表示时间发生的先验概率。

2.3 改进的离散化方法

将文献[8]提出的离散化方法进行改进，结合Naivescaler离散化算法，减少候选离散点的数量，同时选取判别式H1-H2≤H/K来判断是否继续进行离散化。其中H1为本次离散后决策表的信息熵，H2为上次离散后决策表的信息熵，K为该属性的候选离散点的数量。这样不但大大减少了候选离散点的数量，同时避免了原离散化算法需要人为确定阈值的局限[8]。具体步骤为：

(1)按属性值由大到小进行排序。依次判断两相邻实例的属性值和决策值，如果两者都不同，则将两属性值的平均值作为候选断点值，B为候选断点值集，同时计K为属性的候选断点个数，P为已选取断点集。

(2)P=；L={U}；H=H(U)；H1=H。

(3)对每个c∈B,计算H(c,L)，H2=min(H(c,L))。

(4)若H1-H2≤H/K，则结束。

(5)令H(c，L)=H2时断点为cmin，将其加入到P中，B=B-{cmin}。

(6)对于所有X∈L，若cmin将X分为2部分，记为X1和X2，则在L中去掉X并将等价类X1和X2加入到L中。

(7)如果L中各个等价类中的实例都具有相同的决策，则结束；否则转到(4)。

3 Elman神经网络

3.1 模型结构

人工神经网络以其自组织、自适应和自学习的特点，被广泛地应用于故障诊断领域。Elman网络是一种典型的动态递归神经网络，不同于普通的递归网络，其隐含层有一个反馈节点，该节点的延迟量存储了前一时刻的值，并应用到当前时刻的计算，如图1所示(同一水平线的神经元为相同层)。由于Elman网络能够存储供将来时刻使用的信息，因此其既可以在数据训练后对模式产生响应，也可以产生模式输出[9]。

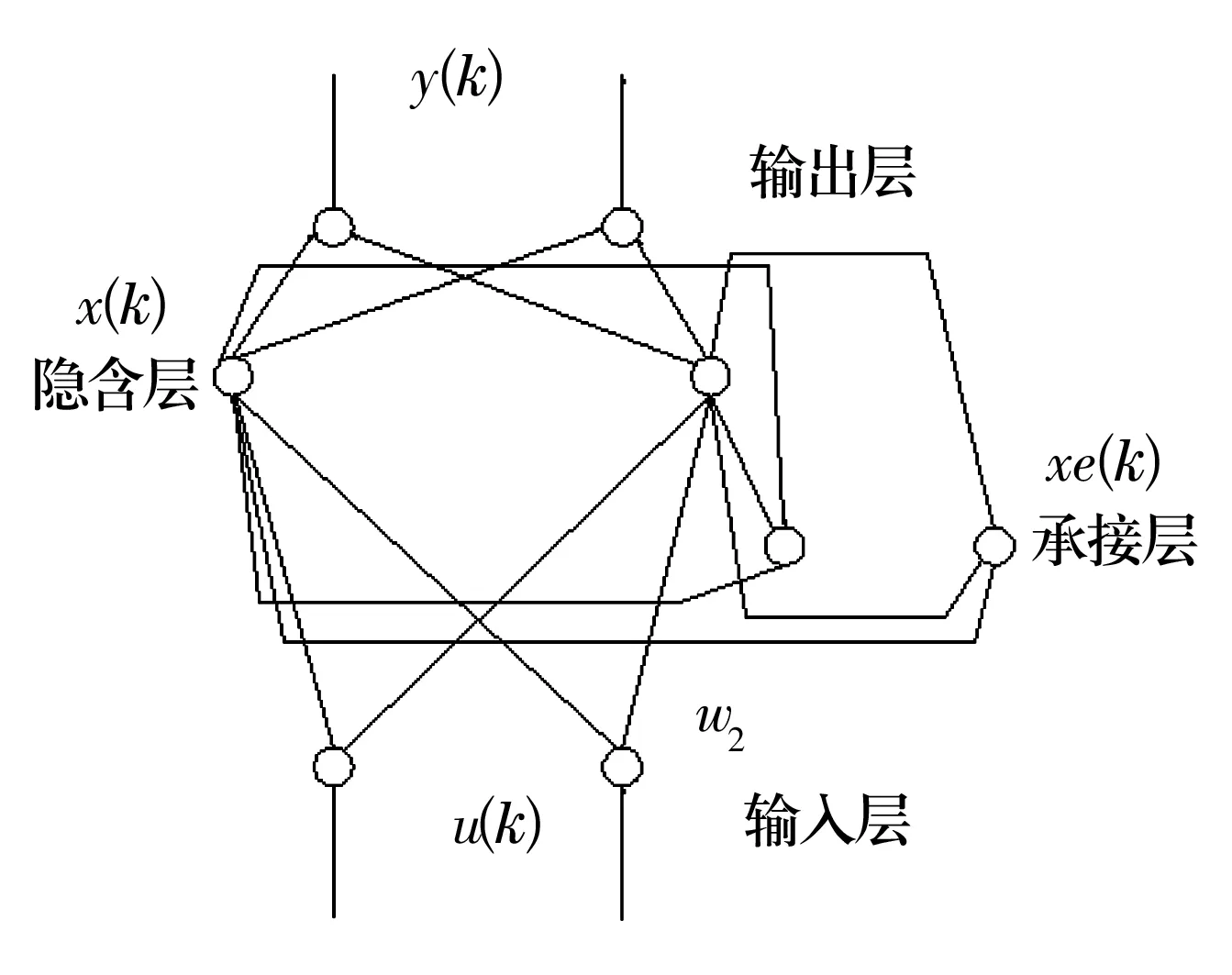
图1 Elman神经网络结构

3.2 模型构建

首先将试验测得的原始数据进行离散化分类处理；然后将结果输入到神经网络中进行训练和预测，充分发挥离散化算法的分类功能，同时减少神经网络的运算时间。故障诊断系统流程图如图2所示。

图2 故障诊断流程图

4 应用实例

以30216圆锥轴承故障诊断为例[10]，根据试验台所测数据进行特征参数选择试验。试验转速为1 200 r/min，轴承径向负荷为599.76 N/cm2，轴向负荷为499.8 N/cm2，采用截止频率为2 000 Hz的低通滤波器对振动信号进行滤波处理。

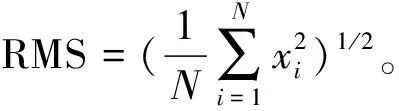
基于粗糙集和神经网络故障诊断系统的诊断过程为：

(1)通过采样处理和归一化处理，得到12组数据作为学习样本，见表1。D为决策属性，当轴承正常时为1，滚动体故障时为2，内圈故障时为3，外圈故障时为4。

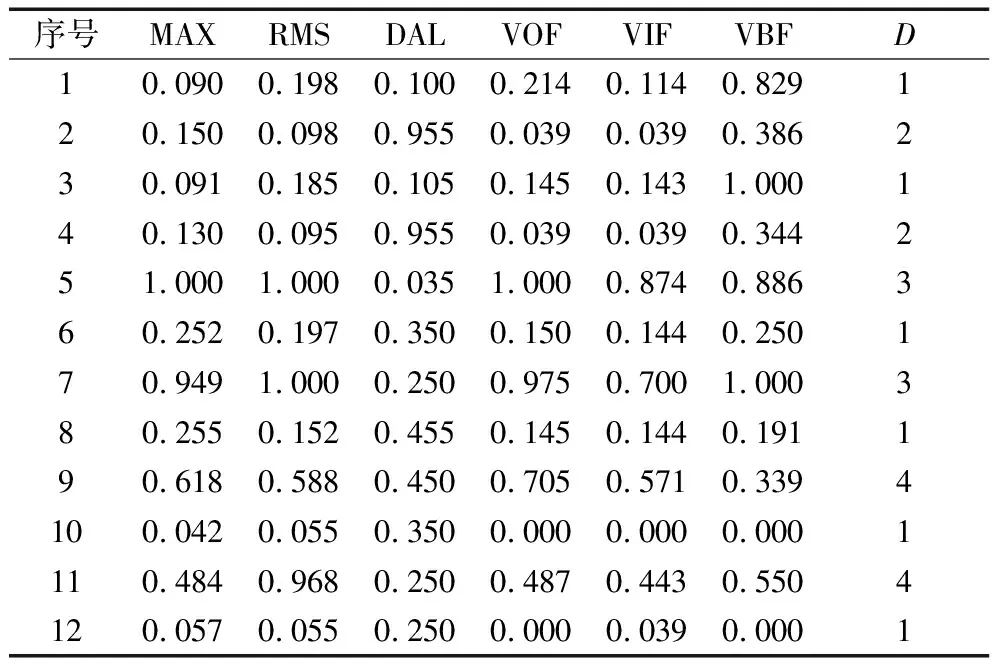
表1 轴承故障信息决策表

(2)应用基于信息熵的改进离散化算法对表1进行离散化处理，结果见表2。

表2 离散化后的故障信息决策表

(3)运用粗糙集理论对离散后数据(表2)进行约简。利用粗糙集软件rosetta可得属性约简结果MAX，DAL和VBF。同时对条件属性相同的样本进行纵向约简，即删除表2中相同的行，结果见表3。

表3 属性约简后决策表

由于决策属性为4种，因此输出节点为4个，设定 {0,0,0,0}为1，{1，0,0,1}为2，{1,0,1,0}为3，{1,1,0,0}为4；隐含层节点为8个，神经网络程序为[11]：

net=newelm(minmax(p),[8,4],{′tansig′,′purelin′});

net.trainParam.show=50;

net.trainParam.epochs=10000; %训练次数

net.trainParam.goal=1e-4; %训练精度

net.trainParam.lr=0.05; %学习速率

net=train(net,p,ceshi);

使用粗糙集理论进行数据处理前后的神经网络训练误差曲线如图3所示。

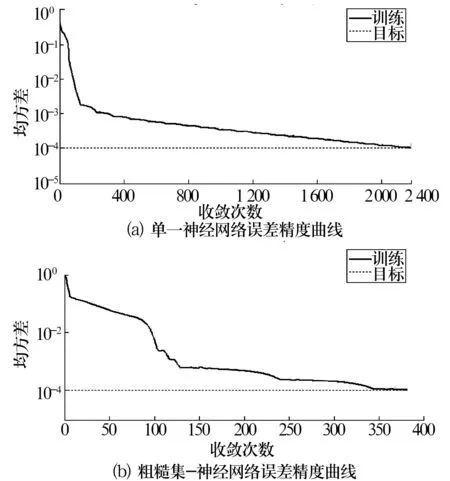
图3 误差精度曲线

为检验算法是否有效，将表4所示检验样本[10]进行属性离散化，粗糙集理论和神经网络系统处理，结果见表5。由结果可知，数据处理后对故障类型的认定与原结果完全一致，确保了诊断的准确率。同时，收敛次数由单一神经网络的2 182次减少到383次，收敛速度大大增加。

表4 故障预测信息决策表

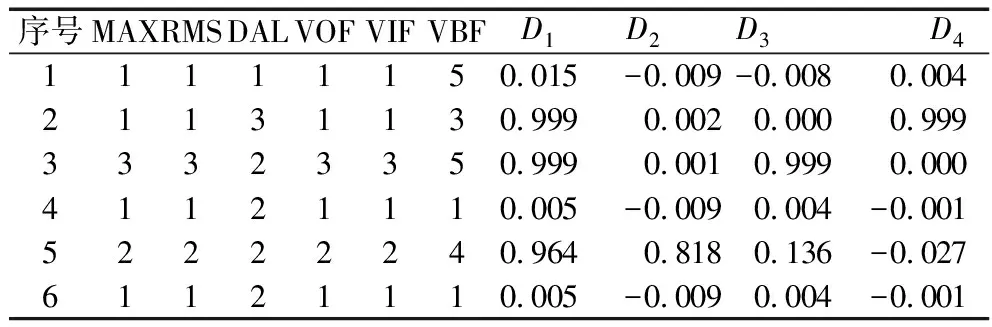
表5 使用粗糙集理论的故障预测样本神经网络结果

5 结束语

试验结果表明，与单一运用Elman神经网络相比，改进的Elman神经网络在保证训练精度的同时，收敛次数从2 182次降到383次，明显提高了数据训练速度，在保证诊断准确性的同时大大提高了故障诊断效率，具有很好的工程实用性。