完全数据下混合weibull分布参数的MCMC估计

罗光华，张清水

（三明学院 教育与音乐学院， 福建 三明365004）

完全数据下混合weibull分布参数的MCMC估计

罗光华，张清水

（三明学院 教育与音乐学院， 福建 三明365004）

混合weibull分布是可靠性分析中的一类 重要的分布 ，假设样本服 从二重混合weibull分 布，即可给出 后验参数估计.本文采用基于Gibbs抽样的马尔科夫链蒙特卡罗方法(MCMC)，设计了 用于参数Bayes估计的抽样 方案,通过 模拟研究，与EM方法进行比较.结果显示，采用Bayes方法估计参数具有一定的优越性.

混合weibull分布;完全数据;Gibbs抽样

1 引言

混合Weibull分布是一个广泛应用于各类可靠性分析的重要分布，对于混合分布的参数估计算法，以往多采用极大 似然 法 或EM算法[1-3]，而 传统极 大 似 然法求 解 过 程相当复杂，EM算法虽然有所简化，但相应的计算形式依然比较复杂.近年来，由于Bayes理论的活跃,让基于Bayes理论的各种MCMC方法倍受关注,通过构造平稳的马尔科夫链，对产生服从后验分布的随机样本进行统计推断[4-6].本文考虑在完全数据下，导出二重单参数weibull混合分布的参数完全条件后验分布后，利用Gibbs抽样算法解决参数估计问题，结果显示以Gibbs抽样算法估计混合Weibull分布参数是一个行之有效的办法.

2 MCMC方法与Gibbs抽样法

MCMC方法是通过建立一个平稳分布为 π(x)的马尔科夫链，待此链运行充分后，马尔科夫链将比较稳定，这时取值分布将与平稳分布足够接近，继而得到一系列样本X(1)，X(2)，…，X(n)做为来自 π(x)的样本，基于这些样本对函数g(X)使用蒙特卡罗积分近似得到数学期望

常用方法主要有Metropolis-Hastings抽样法、Gibbs抽样法及一些对应的复合抽样法，其中Gibbs抽样法是最易实现且应用最广泛的一种MCMC方法[7-8].

Gibbs抽样法可以看做是Metropolis-Hastings方法的特殊例子，利用完全条件分布族迭代抽样，建立平稳分布为 π (x)的马尔科夫链：

（1）选择初始值X0

（2）逐个生成

3 二重weibull混合分布的参数后验估计

假设X=(x1,x2,…,xN)为给定的样本数据，服从二重weibull混合分布，其密度函数如下：

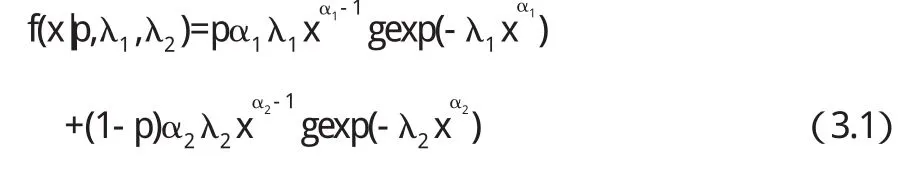
(00,λ2>0)相互独立.

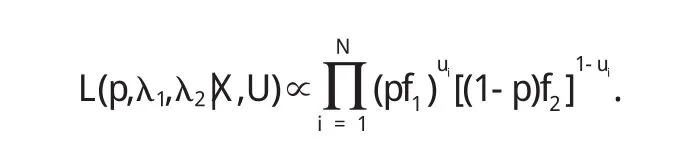
而待估参数为p,λ1,λ2利用贝叶斯估计理论可推导得其联合后验密度

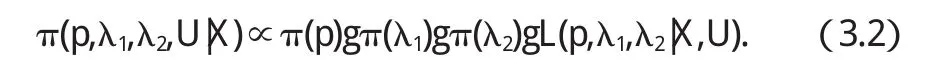
其中 π(p)、π(λ1)、π(λ2)分别为p,λ1,λ2的先验密度.

(1)由 π(U|X,p,λ1,λ2)产生U

由于各标签变量独立可得后验密度

（2）由 π(p|X,U,λ1,λ2)产生p

通过式（2）可知p的后验密度只与U,X有关，所以有

π(p|X,U,λ1,λ2,)∝π(p)gL(p,λ1,λ2|X,U)，取p的先验密度为bera(α,β),则有

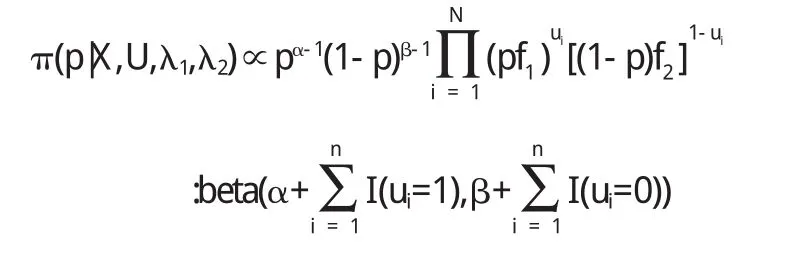
示性函数

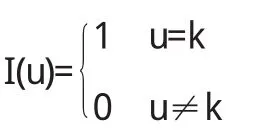
(3)由 π(λj|X,U,p)产生 λj,j=1,2.

按照Jeffreys准则，λj的先验取为由贝叶斯公式得 λj后验密度

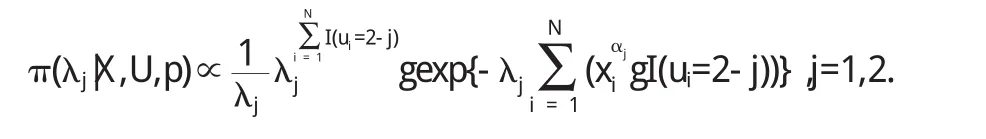
显然

由于已知待估参数的后验分布，可以采用Gibbs抽样法进行抽样，重复(1),(2),(3)步得到一系列样本，去掉前n个不收敛的样本后，根据（2.1）式利用余下样本得到近似期望.

4 模拟与比较

本文采用R软件编写抽样算法及样本处理[9-10]，令不同的样本数k从10到100，分别做随机模拟500次，求得其期望、方差与均方误差.假设混合模型（3.1）的真实参数(p,λ1,λ2) =(0.7,1,4),对于Gibbs抽样，令p的先验服从Beta(1,1)，取初始参数(p(0),λ1(0),λ2(0))=(0.5,2,1),各循环Gibbs抽样15000次，确保样本充分收敛，取后5000次抽样做参数估计.Gibbs抽样估计与EM算法所得估计期望值见表1.

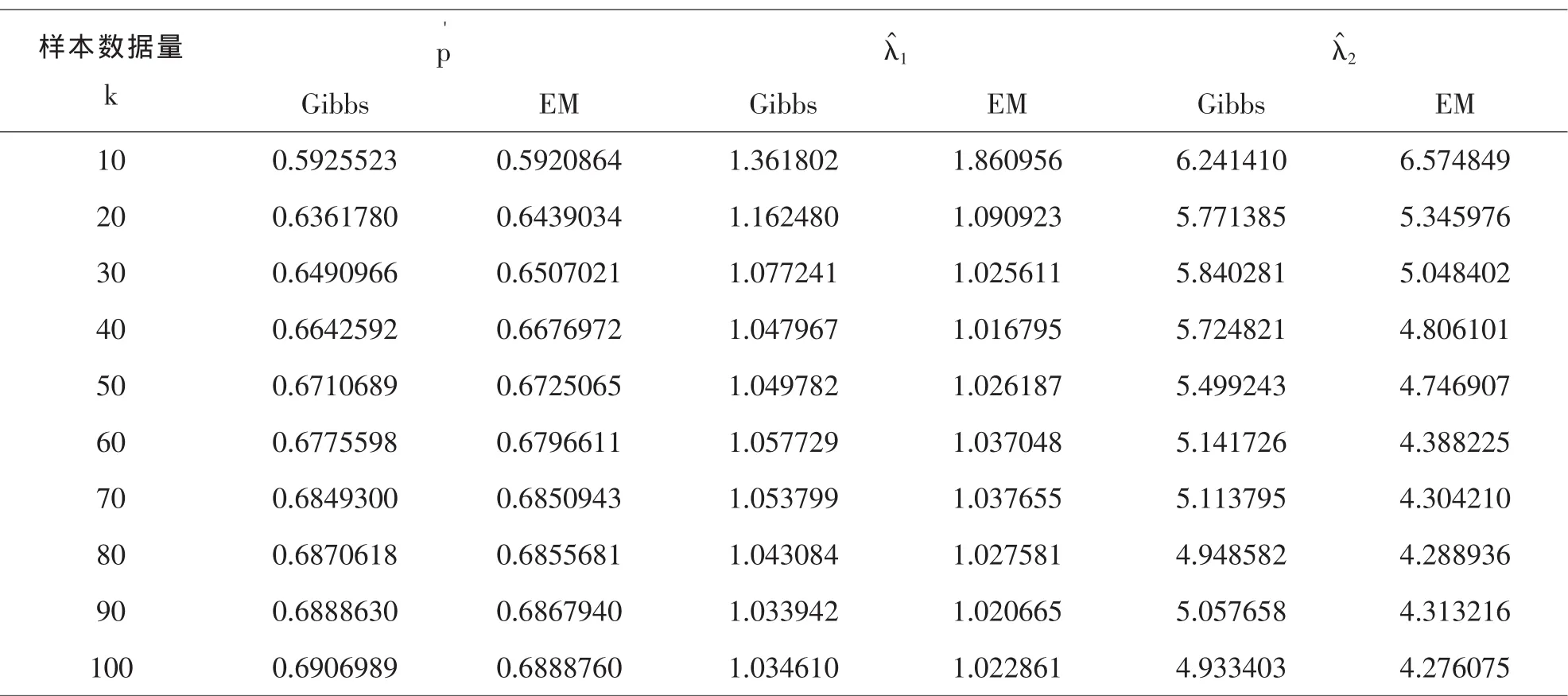
表1 各参数估计期望

可以看出，采用Gibbs抽样法对二重混合weibull的估计是有效的，与EM估计算法结果相比，多数情况下，二者结果大致相当.但在小样本情况下，采用Gibbs抽样的各参数Bayes估计结果会优于EM算法估计，随着样本数的增加，二者估计结果互有优劣，但无明显差别.而均方误差显示Gibbs抽样估计的偏差要好于EM算法 （图1），同时Bayes估计的方差基本上小于采用EM算法的方差，这表明采用Gibbs抽样的Bayes估计相对比较稳定(图2)，并且只有在样本数足够多时，二者的均方误差与方差才接近.因此，当样本数较少时，使用Bayes估计效果更好.

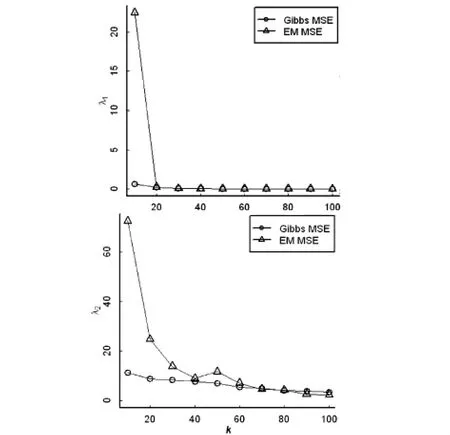
图1 各参数估计的均方误差（MSE）

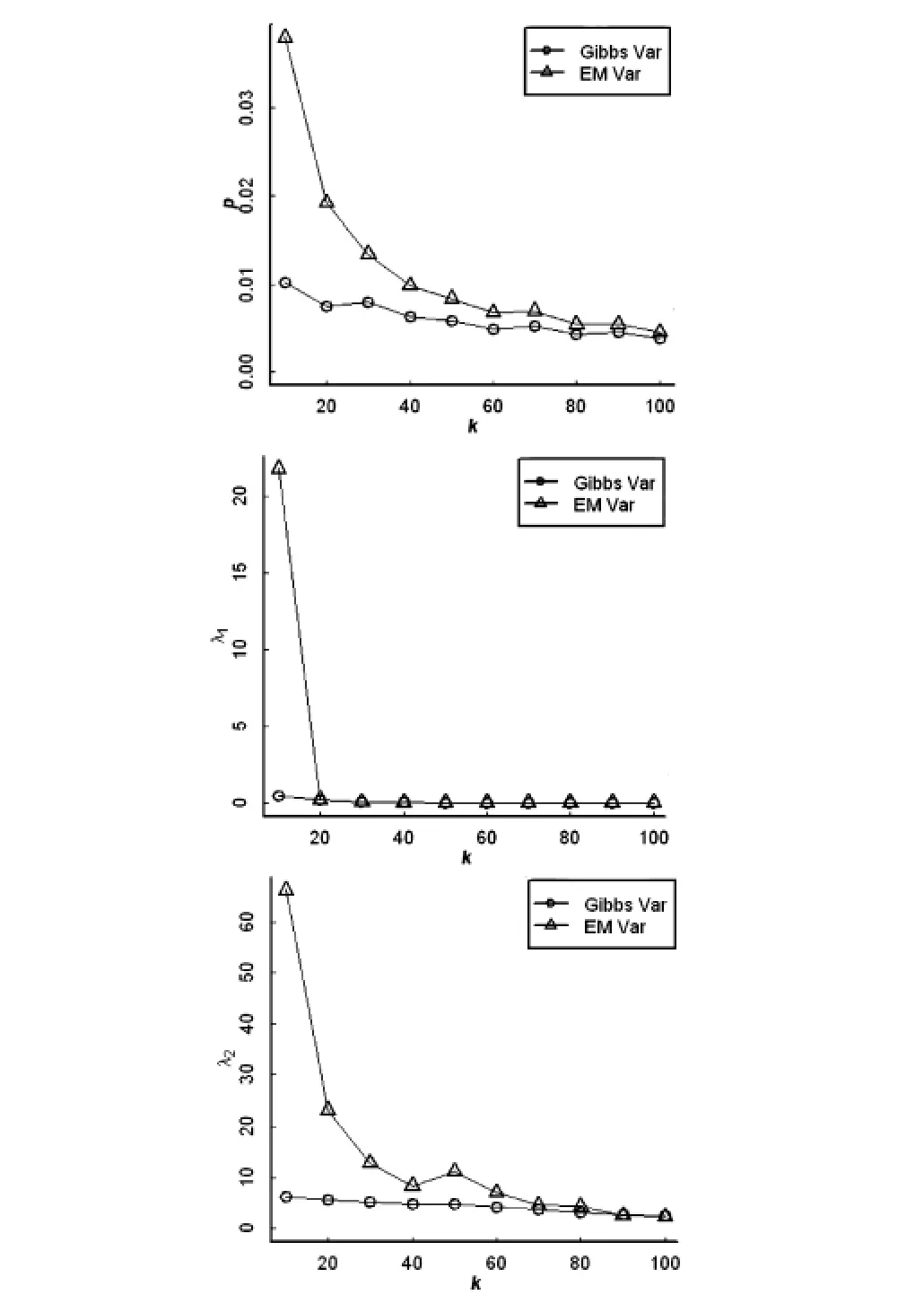
图2 各参数估计的方差（Var）

5 结论

Bayes理论下的MCMC算法及其应用是当今很活跃的一个研究方向，本文采用Gibbs抽样法对二重混合weibull分布的参数进行Bayes估计，得到了较好的估计效果，该方法具有形式简单，易实现且计算量较小等优点.通过模拟比较发现，Bayes估计不易受样本数限制，估计偏差较小且稳定性较好，在样本数较少的情况下尤其适用.

〔1〕朱利平,卢一强,茆诗 松.混合指数分布的参 数 估计[J].应用概率统计,2006,22(2):137-150.

〔2〕杨珂玲,韩慧芳.两混合正态分布的参数估计方法[J].黄冈师范学院学报,2006（03）:16-19.

〔3〕 赵亚林.混合指数分布定数结尾时参数估计的Monte Carlo EM加速算法[J].科技通报，2012，28(5):9-13.

〔4〕刘乐平，袁卫.现代贝叶斯分析 与 现代统计 推 断[J].经济理论与经济管理，2004(6):50-54.

〔5〕刘国旺,熊健.基于MCMC方法的ARFIMA模型贝叶斯分析及实证研究[J].数理统计与管理,2012,31(3):434-439.

〔6〕朱慧明，曾惠芳，郝立亚.基于MCMC的贝叶斯变结构金 融 时 序GARCH模 型 研 究[J].数 理 统 计 与 管 理, 2011,30(6):1009-1017.

〔7〕林静.基于MCMC稳态模拟的指数回归模型及其应用[J].运筹与管理,2005,14(4):95-100.

〔8〕Larry Wasserman(张波,等译).统计 学完全 教 程[M].北京:科学出版社，2008:313-339.

〔9〕Jim Albert.Bayesian Computation With R[M]. New York:Springer,2008:235-282.

〔10〕Ioannis N tzoufras.Bayesian Modeling using WinBUGS [M].New Jersey:Wiley,John&Sons,Inc,2009:305-325.

O212.8

A

1673-260X（2014）06-0009-03

三明学院自然科学基金项目(B201016/Q)