概率论在高等数学中的应用研究

张晓梅，李红梅

（四川文理学院 数学与财经学院， 四川 达州635000）

概率论在高等数学中的应用研究

张晓梅，李红梅

（四川文理学院 数学与财经学院， 四川 达州635000）

高等数学是难度较大的学科，其中很多计算、证明问题如果找不到正确方法就很难进行解答.然而在解题时如能恰当运用概率论知识不但可以提高解题效率，而且还能帮助学生树立解答数学问题的信心.本文通过对概率论的相关知识进行介绍，详细探讨了概率论在高等数学中的应用，以期为提高高等数学教学效率提供参考.

概率论；高等数学；应用；研究

概率论是研究随机现象数量规律的数学分支，在解答高等数学证明问题时，巧妙的利用概率论能化难为易，达到事半功倍的解题效果，从而培养学生学习高等数学的兴趣.

1 概率论概述

人们对概率的研究始于17世纪中期，直到18世纪概率论才得以迅速发展，其中瑞士数学家雅科比·伯努利是概率论发展的奠基人，他提出著名的“伯努利大数定理”，其含义为：在多次的重复试验中，频率表现出逐渐稳定的趋势.该定理的提出推动了概率论的发展，概率论也从此被广泛应用于人类生产生活的不同领域中.

概率论是数学的一个分支，由法国数学家普拉斯在19世纪初期完成概率论学科的体系构建，其在《概率的分析理论》中对概率进行明确定义：全体共包括N个事件，假定其相同程度确定，发生E情况共由n个事件组成，则E情况发生的概率为n/N.

概率论理论发展到今天已非常成熟，在农业技术、军事、工程技术、生物学、物理学等领域应得到了广泛应用，提高了人们对事件发生的研究水平，为人类社会的发展和进步奠定了坚实的基础.

2 概率论在高等数学中的应用

高等数学中部分题目难度较大，如果采用传统的思路进行分析，不但解题过程繁琐，而且得出正确结果的可能性较小.此时如将概率论引入到解题过程中，往往能够迅速得出结果.下面对概率论在不同数学题目中的应用进行探讨，以供解题参考.

2.1 利用概率分布简化解题过程

概率分布是概率论知识中的基础概念，利用概率分布性质可以简化解题过程，提高解题效率.实际解题时可利用处于0～1之间的数字构造某些事件发生的概率，借助概率分布知识最终达到解题的目的.利用该种解题方法可简化解题过程，提高计算结果的准确性，从而使学生更为清晰的了解高等数学与概率论间的内在联系，进而培养学生学习高等数学的兴趣.

这一题目时，需首先对其进行分析.即依据不均匀规则将一枚硬币共抛出A次，每次硬币掉落在地面上时正面朝上的概率为P=x/x+y，在上抛A次整个过程中出现正面次数用字母T表示，于是P={T=k})，由分布规律理论可知：

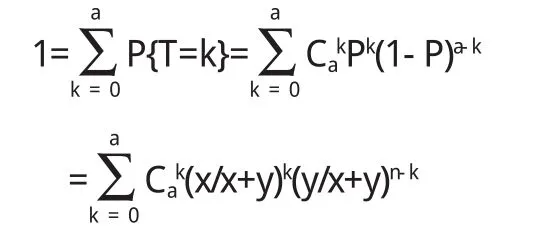
最后便可顺利的得出该题目的计算结果：

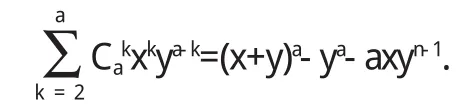
又因为Eζi=Dζi=1，由同分布中心极限定理知：

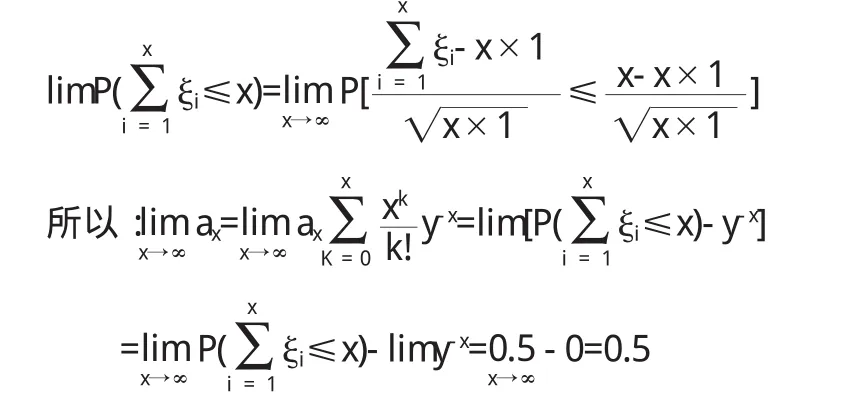
2.2 概率论在计算级数与广义积分的应用

概率论知识中方差和数学期望是随机变量具有的特征，借助随机变量数学期望与方差存在的关系，可解答高等数学中求解级数和广义积分类型的题目.

首先，在高等数学中求解级数是难度较大的题目，因此更应注重数学期望与方差知识的引入，进而化简解题过程，得出结果.

其次，解答高等数学问题时可变形被积函数，将其转变为正态分布随机变量的数学期望，再进行适当运算，便能顺利的解答出相关题目.

最后，计算积分时可采用分布计算法，但是利用该种计算方法需要多次运用分布积分法，同时还要进行极限的计算，因此计算过程十分繁琐.为高效的解答出相关题目，可借助指数分布随机变量的数学期望解答相应题目，以降低解题难度.

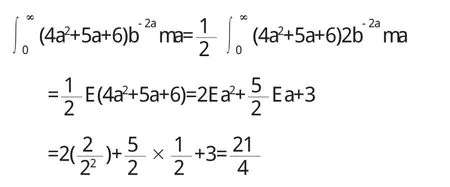
3 概率论在高等数学不等式证明中的应用

高等数学中不等式的证明是较为典型且具有一定难度的一类题目，部分学生在解答该类题目时往往不知从何下手.其实只要适当引入概率论内容，有些问题便可迎刃而解.

例如，已知b=1，2，3...n，xb≥0，求证不等式成立.解答该题目时应先将模型建立起来，即假设随机变量 ζ 为P（ζ=xb）1/n,b=1,2,3...n，且当xb=0时公式明显成立.当xb＞0时，定义函数f（a）=lna（a＞0），则f（a）=lna（a＞0）为上凸函数.由f（Eζ）≥Ef（ζ）[4]可知：

两边取e为底的指数，则可得

4 总结

很多高等数学题目难度较大，为降低解题难度，教学实践中教师应帮助学生正确理解概率论的相关概念，并积极的鼓励和引导学生使用概率论知识分析数学问题，寻找出简单的解题思路，进而提高解题效率，保证计算结果的正确性，帮助学生树立起解答数学问题的信心，逐步培养其学习高等数学的热情.

〔1〕许丽利.浅谈概率论在高等数学中的应用[J].兰州教育学院学报,2013（03）:118-119+122.

〔2〕卓泽强,魏文玲,李小龙.概率思想在 高等数学计 算中的应用研究[J].科技资讯,2010（20）:196-197.

〔3〕卓泽强,魏文玲,李小龙.概率思想在 高等数学证 明中的应用研究[J].科技资讯,2010（30）:177.

〔4〕李瑞军.如何促进学生学习概率论的主动性［J］.北京电力高等专科学校学报(社会科学版),2012（10）.

O211

A

1673-260X（2014）06-0004-02