离散正奇异切换系统的稳定性

黄丽琼

（商洛学院 数学与计算机应用学院，陕西商洛726000)

离散正奇异切换系统的稳定性

黄丽琼

（商洛学院 数学与计算机应用学院，陕西商洛726000)

通过分析离散正奇异切换系统解的结构和解的正性要求，运用一个辅助的正标准切换系统，给出离散正奇异切换系统在任意切换信号下是稳定的两个充分条件。并给出数值算例验证结论的可行性。

正系统；奇异系统；切换系统；稳定性

切换系统是混合系统的一种，切换系统是由一系列的动态子系统和一种切换策略构成，该策略协调子系统之间的运行。离散正奇异切换系统是指切换系统中的每一个子系统都是正系统。现实生活中有很多动态子系统都是这类奇异切换系统，例如，通信系统，化学反应系统，电路网络系统。1999—2006年，Liberzon和Morsc等众多学者对一般奇异切换系统的稳定性和可稳定性进行了大量的研究[1-8]。2006—2010年，Robert Cimochowski对离散正标准切换系统的稳定性进行了研究[9-11]，2011年，Ettore Fornasini对离散正标准切换系统的稳定性和可稳定性进行了系统的分析和整理。Cimochowski对离散正标准时滞切换系统的稳定性进行了研究[12]。本文主要讨论了离散正奇异切换系统在任意切换下的稳定性问题。

本文用到的记号基本都是标准的。具体地，Rn为n维实向量空间，为n维非负实向量空间，C为复数集，N为正整数集，N0为非负整数，AT为矩阵的转置，rank(A)为矩阵A的秩，A-1为矩阵A的逆矩阵，AD为矩阵A的Drazin逆,即满足下列3个式子：1)ADAAD=AD，2)ADA=AAD，3)Ak+1AD=Ak，k≥ind(A)，A＞0表示矩阵A是正定的，A＜0表示矩阵A是负定的，表示矩阵A是正的，即A的每一个元素都是正的。

1 定义

考虑离散正奇异切换系统

其中x(k)∈Rn是系统的状态，映射δ：N0→M是任意切换信号，M={1，2，…，m}是一个指标集，设系统(Ei，Ai)为系统(1)的第i个子系统，δ(k)∈i，i∈M表示第i个子系统激活，rank(Ei)=r＜n，i∈M。

定义1[10]如果存在一系列λi∈C，i∈1，2，…，m，使得det(λiEi-Ai)≠0，则称系统(1)是正则的。

考虑离散正奇异系统

根据文献[13]知，如果系统(2)是正则的，则存在两个非奇异矩阵M，N，使得

其中撰为幂零的,J为Jordan标准型。

如果系统(2)是正则的,则系统(2)的解能够唯一表示为

定义2[13]如果对每一个可容许初始状态，系统(2)的状态轨迹都是非负的,即，则称系统(2)是正系统。

定义3[12]奇异切换系统(1)是正系统,当且仅当系统(1)的所有子系统都是正系统。

定义4[9]奇异系统(2)是渐近稳定的,当且仅当(3)式满足条件。

定义5[13]如果系统(2)是正则的且，则系统(2)是正系统当且仅当。

2 引理与定理及其证明

假设1离散正奇异切换线性系统(1)满足。

引理1假设1成立，则离散正奇异切换系统(1)的解可由一个可容许的初始状态x(0)唯一给出

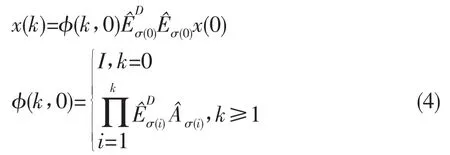
证明在考虑切换系统(1)的唯一解时，由于一个状态跳跃会出现在切换瞬间，导致在上一个切换下系统最后所到达的状态或许不是下一个子系统激活状态下的可容许初始条件，因此，首先考虑一个在k步内没有切换的系统，给出一个可容许初始状态x(0)，则这个系统在k步的解为，则x(k)必须是第k+1步处子系统的可容许初始状态，即

而(5)中所给出的条件和假设1是等价的，所以假设1成立，系统(1)的解可由(4)式唯一给出。

定理1设假设1对系统(1)成立，如果存在m个向量满足条件，则称系统(1)在任意切换下是稳定的。

证明假设1对系统(1)成立，x(0)是的一个可容许初始条件，则由(4)式得到φ(k，0)满足递归方程，则系统(1)在假设1下能转变为

切换系统(6)是稳定的，则切换系统(1)就是稳定的，定义，则系统(6)可写为，选择李亚普诺夫函数

由于V(x，x(k))满足任意的切换率，

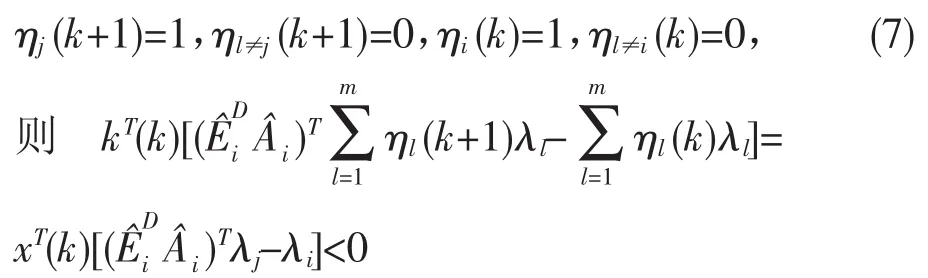
所以对(7)式的特殊配置也是成立的。

则得到V(x，x(k))≥0且为递减的，因此切换线性系统(6)是稳定的，即原奇异切换线性系统(1)是稳定的。

引理2[14]若系统(1)是正系统，任意固定一个切换信号σ，xa(·)，xb(·)是系统(1)的解，xa(0)，xb(0)是系统(1)的初始状态，如果，则xb(·)。

引理3[14]设假设1成立，如果存在m个向量满足

证明假设条件(8)成立，对任意的i，j∈M，存在一个足够小的mij＞0，则

则(10)式是成立的。

定理2设假设1对系统(1)成立，如果存在m个向量满足条件(8)，则称系统(1)在任意切换下是稳定的。

证明由于假设1对系统(1)成立，如果存在m个正向量满足条件(8)，任意给定一个切换σ：N0→M，则对任意给定的一个常数ε＞0，总存在一个常数v＞0使得||vλi||＜ε，(i∈M)，选择， i∈M根据引理3则存在一个0＜u＜1，使得

其中xvλ是系统(1)在初始状态vλ下的解。

设初始条件x(0)满足||x(0)||＜σ=v min{τ1，τ2，…，τn}，τi是λ的第i个元素，则

其中xx(0)是系统(1)在初始状态x(0)下的一个解，因此得到

注定理1与定理2中的条件为相互补充的条件，不能被相互替换，可参看例题。

例1考虑具有如式(11)参数的正奇异切换系统

存在两个向量λ1=[98.3405,81.9584,76.3041]，λ2=[100.8940,78.7394,83.2246]使得定理2中的条件，∀i，j∈M成立，通过定理2可知正奇异切换系统是稳定的。然而不存在向量λ1，λ2使得定理1中的条件， j∈M，成立。

[1]Liberzon D,Hespanha J P,Morse A S.Stability of switched systems：A lie algebraic condition[J].Systems and Control Letters,1999,37(3)：117-122.

[2]Narendra K S,Balakrishnan J.A common lyapunov function for stable LTI systems with commuting amatrices[J].IEEE Transactions on Automatic Control,1994, 39(12)：2469-1471.

[3]Shorten R N,Narendra K S.On the existence of a common lyapunov dunction for linear stable switching systems[J].Yale Workshop on Adaptive and Learning Systems, 1998,10(4)：130-140.

[4]Cezayirli A,Ciliz MK.Transient performance enhancement of direct adaptive control of nonlinear systems using multiple models and Switching[J].IET Control Theory and Applications,2007,1(6)：1711-1725.

[5]Liberzon D,Morse A S.Basic Problems in stability and design of switched systems[J].IEEE Control Systems Magazine,1999,19(10)：59-70.

[6]Sun Z,Ge S S.Analysis and synthesis of switched linear control systems[J].IEEE Transactions on Automatic Control,2005,41(2)：181-195.

[7]Xie G,Zheng D,Wang L.Controllability of switched linear systems[J].IEEE Transactions on Automatic Control,2002,47(8)：1401-1405.

[8]Xu S Y.Robust Control and filtering of singular systems [M].Springer-Verlag Berlin Heidelberg,2006：201-208.

[9]杨冬梅,张庆灵,姚 波.广义系统[M].北京：科学出版社,2004：69-80.

[10]Cimochowski R.Stability of positive switched discretetime linear systems[C].Methods and Models in Automation and Robotics,15th International Conference,2010：207-211.

[11]Fornasini E,Valcher ME.Stability and stabilizability criteria for discrete-time positive switched systems[J].IEEE Transactions on Automatic Control,2011,57(5)：1208-1221.

[12]Liu X W.Stability Analysis of switched positive Systems：a switched linear xopositive lyapunov function Method[J].IEEE Transactions on Circuits and Systems-II：Express Briefs,2009,56(5)：414-418.

[13]Virnik E.Stability analysis of positive descriptor systems[J].Linear Algebra and its Applications,2008, 429：2640-2659.

[14]Liu X W,Gao X.New stability condition for positive switched linear systems[J].Journal of Southwest University for Nationalities：Natural Science Edition, 2010,36(2)：262-268.

（责任编辑：李堆淑）

The Stability of the Discrete Positive Singular Switched System

HUANG Li-qiong
(College of Mathematics and Computer Application,Shangluo University,Shangluo 726000,Shaanxi)

Through analysis of the solution structure and the positivity of the positive singular switched system,an auxiliary positive standard switched system is adopted to explore two sufficient conditions for stability under arbitrary switching.And a numerical example is given to illustrate the validity of the proposed conditions.

positive system;positive singular system;switched system;stability

O231

：A

：1674-0033（2014）06-0016-03

10.13440/j.slxy.1674-0033.2014.06.006

2014-05-10

商洛学院科研基金项目(14SKY008)

黄丽琼，女，陕西洛南人，硕士，助教