中学生感知的数学教师学科教学知识的结构与特点

徐彦辉

（温州大学 数学与信息科学学院，浙江 温州 325035）

1 引 言

众所周知，教师品质是影响学生学习最重要的一个因素，但是，学界对教师品质的准确定义还远未达成一致的看法．也即是，教师的优秀品质有哪些构成要素，如何培养优秀的教师，等等，这些问题仍然是学界长期争议和值得进一步研究的问题．在此，作为改进教师品质的一个至关重要的要素，Shulman（1986）首次提出了PCK（Pedagogical content knowledge）这个概念，引起了学界广泛的关注、争论和质疑．Shulman提出的PCK对教师教育研究是一个独特的贡献，因为PCK解决的是如何教授学科内容和如何理解学生思考的问题，它指引着人们关注教师教育中长期相互分离的两个最重要的因素——学科知识和教学法知识．PCK的提出给予教师知识研究以新的活力，提供了一个组织和收集教师认知资料的新的分析框架，突出了学科知识及其在教学中转变的重要性，提供了一种更完整的研究教师知识和课堂实践的视角．PCK是一种特殊的教师知识，它对于理解有效的教师需要什么知识至关重要．教师需要PCK以组织课堂中的内容，发展所教主题可充分了解的表示，理解学生在学习特定主题时可能遇到的困难．但是，PCK又是一个意义含糊且复杂的概念，难以清晰地界定出它的确切含义，很难被看作为是一个独立的概念，需要大量的解释．确定实践中PCK所包含的特定组成成分则更困难，PCK更多是一种内在的建构，而不能很容易地被观察．很少有研究能真正把握PCK的真正含义和所包含的特定组成成分，测量教师的PCK，设计、实施和分析方法都是很困难和非常费时的．

2 问题提出的理论依据

学科教学知识（PCK）首先是由Shulman在1986年所提出，根据Shulman最初的界定，PCK即为关于教师将自己所掌握的学科知识转化成学生易于理解的形式的知识，它具体表现为教师知道使用怎样的演示、举例、类比等来呈现学科内容，知道学生的理解难点[1]．Shulman（1987）认为PCK是专业学科知识与教育学知识的综合去理解特定主题的教学是如何组织、呈现以适应学生不同兴趣和能力的，即教师在面对特定的主题时，如何针对学生的不同兴趣与能力，将学科知识加以组织、调整与呈现，并进行教学方面的知识[2]．随后许多学者对 PCK有不同的定义．如：Tamir（1988）认为PCK的构成要素为：（1）学生及其学习的知识；（2）课程知识；（3）教学知识；（4）评价知识[3]．Smith和Neale（1989）将PCK概括为4个组成部分，即：学生概念的知识；教学策略知识；形成和阐述内容的知识；课程材料与活动的知识[4]．Marks（1990）提出PCK包括：学科的教学目的、学生对学科的理解、教学媒介的知识、教学进程[5]．Carter（1990）认为PCK是教师知道相关的学科内容，并且知道如何把他们转译成课程事例的知识[6]．Grossman（1990）认为PCK包括4个部分，即：（1）教师关于一门学科教学目的的统领性观念——关于学科性质的知识、关于学生学习哪些重要内容的知识或观念；（2）关于学生对某一课题理解和误解的知识；（3）关于课程和教材的知识，它主要指关于教材和其他可用于特定主题教学的各种教学媒体和材料的知识，还包括了学科内特定主题如何在横向和纵向上组织和结构的知识；（4）特定主题教学策略和表征的知识[7]．Gudmundsdottir（1991）认为PCK是一种教师把内容知识转型成在教学中实际利用的与先前不同形式的隐含知识[8]．Cochran，King和 DeRuiter（1991）从建构主义的观点定义PCK是一种综合了教师的教学法、学科内容、学生特性和学习情境等知识的统整了解[9]．Magnusson，Borko和Krajcik（1994）将PCK描述为在促进学生知识发展的教师知识中是最重要的结构[10]．Fernandez-Balboa（1995）认为PCK包括5个组成部分：（1）学科知识；（2）关于学生的知识；（3）教学策略知识；（4）教学环境知识；（5）关于教学目的的知识[11]．为了确定PCK的本质和结构，Van Driel等（1998）比较了不同研究人员对PCK的定义，发现他们之间没有一致认同的概念，但几乎所有研究人员都一致认为PCK有两个核心成分，即：（1）了解学生特定的学习困难，（2）具有用以克服这些困难的学科表征的知识[12]．de Berg和Greive把PCK定义为“学科知识被转化成适合于学生学习的形态”[13]．Magnusson等（1999）将PCK叙述为教师帮助学生了解特定学科内容的知识，这包含了特定学科内容主题、问题与论点的组织与表征、适应不同能力与兴趣的学生的教学表征．PCK包括5个组成部分，即：（1）学科教学的倾向；（2）关于学科课程的知识和信念；（3）关于学生理解特定主题的知识和信念；（4）关于学科评价的知识和信念；（5）关于学科教学策略的知识和信念[14]．Carlsen（1999）强调理解学生错误概念的重要性，提出应将“理解学生的错误概念”作为PCK的一个组成成分[15]．W. R. Veal（2000）认为PCK的构成要素为：（1）学科知识；（2）关于学生的知识；（3）情境知识；（4）环境；（5）学科性质；（6）课堂管理；（7）社会文化知识；（8）评价；（9）教学法知识；（10）课程知识[16]．全美教师资格鉴定委员会（NCATE）把学科教学知识界定为：通过学科内容知识和有效教学策略交互作用（intersection）帮助学生有效地学习学科内容的知识；它要求教师在完全理解所教内容、了解和掌握学生的文化背景、先前知识和经验的基础之上，运用多种方式进行教学[17]．

数学教育界有关PCK的研究也不少，如An等人（2004）将“学科教学知识”定义为有效教学的知识，包含3个方面的内容：内容知识、课程知识以及教学知识，并强调了这3种知识之间的联系[18]．田宏根和杨军（2007）认为 MPCK是关于教授某一具体内容的方式或方法的知识．具体地说，是指教授某一特定内容时，有多少有效或不太有效的方式？这些方式是什么？这些方式有什么优缺点？学生在理解某一特定数学概念时，可能会有哪些困难？有什么较为容易的方式让学生掌握？[19]Ball等人（2008）认为“学科教学知识”主要包含了 3个领域的内容：（1）关于内容与学生的知识（KCS）；（2）关于内容与教学的知识（KCT）；（3）关于内容与课程的知识[20]．景敏（2008）认为“数学学科教学知识”是把数学知识与一般教学法知识、有关学生的知识、有关数学学习的知识等整合在一起所形成的知识，是把科学形态的数学有效地转化为教育形态的数学的知识[21]．黄毅英，许世红（2009）认为数学学科知识（MK）、一般教学法知识（PK）和有关数学学习的知识（CK）这3类知识的综合与融合就是数学学科教学知识（MPCK）[22]．童莉（2010）认为MPCK是指关于某一特定的数学内容该如何进行表述、呈现和解释，以使学生更容易接受和理解的知识．并指出MPCK由两核心五成分构成：（1）特定数学内容与教学联合的知识，包括：① 怎样按有意义的顺序来组织和呈现数学内容？② 为了促进学生的理解应该提供哪种或哪些形式的表达方式（解释、图形、符号、情境和操作等）？；（2）特定数学内容与学生联合的知识，包括：① 学生在特定数学内容的学习中会遇到什么困难？② 学生有哪些看法或误解？③ 教师所使用的教学方法是怎样处理学生的困难和误解的？[23]董涛（2010）认为，数学课堂教学中的PCK含有5个构成成分：数学教学的统领性观念、内容组织的知识、学生理解的知识、效果反馈的知识和教学策略的知识[24]．梅松竹等（2010）认为MPCK为关于特定的数学内容或专题，如何进行表述、解释、示范和操作，以使学生更容易理解和掌握及预见和消除学生对特定数学内容的学习困难和误解的知识[25]．李渺，宁连华（2011）认为MPCK是由数学学科知识（MK）、一般教学法知识（PK）、有关数学学习的知识（CK）以及教育技术知识（TK）融合而成．其中，MK有4个维度（数学观念、学科内容知识、数学思想方法以及数学史知识）；PK有4个维度（教育观念、教育理论知识、课程知识以及教学知识）；CK有 3个维度（学生发展的知识、学生学习的认知因素与非认知因素知识以及学习环境的知识）；TK有两个维度（有关传统教学媒体的知识以及有关现代教育技术的知识）[26]．

从上述学者对PCK的定义，可看出PCK包含的范围是极为广泛的．它涵盖了学科的内容、转型、表征，学生的知识、能力与兴趣，以及教学情境．正如Loughran，Gunstone，Berry，Milroy和 Mulhall（2000）所主张PCK是一个有相互影响元素的混合物，当这些元素结合时赋予PCK深刻的理解，如同元素的混合物总是在变化，PCK本身也具有多变性，改变其中任何一个元素将无可避免地影响PCK本质的描绘[27]．同时，已有的研究对于“PCK（或 MPCK）的内涵和构成要素”也存在很大分歧，没有一个清晰的、统一的阐述，且多使用诠释研究法，探讨焦点都是在教师身上．从纷繁的 PCK（或 MPCK）的内涵和构成要素的现象背后，要看到本质，PCK（或MPCK）的内涵和构成要素究竟应该包括哪些内容？在此，学生对教师教学的知觉可提供教师可参考的资料（Brophy 和 Good，1986）[28]．正如 Kennedy（1998）提到PCK是教师的一种特殊知识，除必须抓住所要讲授概念的意义外，还要能由类比、隐喻或其它方式让学生理解，因此学生对教师之PCK应有所感知才是[29]．Fraser（1986）提出教室气氛之研究方法有系统观察、个案研究和纸笔测量，其中以纸笔知觉测量之优点最多：较经济；学生可由较多的学习经验来回答，不像观察资料只是少数的单元；由全体的学生判断而不仅是单一的观察者[30]．虽然 Baxter和Lederman（1999）对采用Likert-type作为评估教师PCK持保留的看法[31]．但段晓林等（1998）曾发展学生对教师学科教学知识问卷[32]．王国华等（1998）以此问卷探讨学生在教室环境中对科学教师学科教学表现的感受，显示以学生填答量表来探讨教师PCK的确是一可行的方式[33]．张静仪，戴翠华（1992）作了“国小学童感知自然教师PCK量表”之效化研究，得到PCK量表的5个因素结构，即：鼓励学生参与、使用教学媒体、学科与课程、评价与了解学生和教学表征[34]．研究基于张静仪，戴翠华（1992）研究的基础上，调查中学生感知的数学教师学科教学知识的结构与特点，以有利于研究数学教师PCK成长的需要，以及帮助中学数学教师能由学生对其PCK的感知，以作为改进教师自己教学的依据，这是一个值得尝试和努力的方向．

3 研究工具和过程及方法

2.1 研究工具

研究借鉴了张静仪等（1992）设计的问卷，并结合文献[1～34]所提出的PCK（或MPCK）的内涵和构成要素，针对鼓励学生参与、使用教学媒体、学科与课程、评价与了解学生和教学表征5个因素，结合数学学科的特征，广泛搜索并整理“PCK（或MPCK）的内涵和构成要素”条目，并向两位多年从事数学教学学科教学知识研究的学者和中学数学高级教师咨询，设计出“数学教师学科教学知识”问卷的初始项目；再将设计好的“数学教师学科教学知识”调查问卷，再次向中学数学教师和学生询问，就问卷设计广泛征求中学数学教师和学生的建议，将有歧义、表述不清或表面效度高的题目排除或者修改．最后，请3位熟悉该研究的数学教育研究人员对问卷项目进行讨论和修改，从理论上明确问卷各项目的合理性，并适当再进行修改，得到一个由38个项目组成的“数学教师学科教学知识”调查问卷．问卷中的每个项目采用5等级评分，“总是如此”记5分，“时常如此”记4分，“有时如此”记3分，“很少如此”记2分，“从未如此”记1分．

2.2 研究过程与方法

2.2.1 被试选择与施测

被试选择：选取温州市市区重点初中、农村普通初中各一所，从这两所初中随机分班整群抽取初一至初二年级的初中生，共409人；选取温州市市区重点高中、农村普通高中各一所，从这两所高中随机分班整群抽取高一至高二年级的高中生，共390人；其中，重点中学414人，普通中学385人．通过检核问卷作答情形，如有学生不按规定答题或仅有单一选答（如所有题目均勾选“有时如此”选项）的情形，则将问卷判为废卷，整个问卷有效率为98%．其中，用于探索性因素分析的问卷共391份；用于验证性因素分析的问卷共392份；两部分样本是随机对半分的，在分布上没有显著差异．

问卷施测：调查采用以班级为单位的团体测量方式，全部由研究者担任主试，采用统一的指导语，问卷当场回收，测试时间约15分钟．

2.2.2 数据分析过程

数据主要通过SPSS 11.5和AMOS 7.0进行统计分析．利用SPSS 11.5对问卷进行项目分析和探索性因素分析，利用AMOS 7.0对问卷进行验证性因素分析．

4 研究结果

4.1 探索性因素分析

首先，采用p值法和题总相关法对量表题目的区分度进行了项目分析，将临界比率值过低和题总相关系数小于0.20的题项剔除．这样删除第9题．

再采取“逐步探索”的方法进行因素分析．

第一步，对37个题目用主成分分析法抽取因素，采用最大正交旋转法，结果抽取到7个因子．但从7个因子所包含的测题来看，比较混乱，归属不够清晰．在特征值大于1的7个因素中，由于第12、13、17、23、25、32、35题在两个因子负荷值相差不大（小于0.1），不好解释，因此删除这7个题目．

第二步，再对剩下30个题目用主成分分析法抽取因素，采用最大正交旋转法，结果提取到特征值大于 1的因素 6个，但由于第7、14、28、36题在两个因子负荷值相差不大（小于0.1），不好解释，因此删除这4个题目．

第三步，再对剩下26个题目用主成分分析法抽取因素，采用最大正交旋转法，结果提取到特征值大于 1的因素 5个，但由于第15题在两个因子负荷值相差不大（小于0.1），不好解释，因此删除第15题．

第四步，再对剩下25个题目用主成分分析法抽取因素，采用最大正交旋转法，结果提取到特征值大于 1的因素 5个，但由于第16题在两个因子负荷值相差不大（小于0.1），且在每个因子上的负荷都比较小（小于0.4），不好解释，因此删除第16题．

第五步，再对剩下24个题目用主成分分析法抽取因素，采用最大正交旋转法，结果提取到特征值大于 1的因素 5个，采用同质性检验，发现：题项10、21和22与其余题项的同质性不高，因此删除第10、21和22题．由于第11、18题与所在因子内容不一致，因此删除第11和18题；这样，第四因子只包含两个项目，根据每一个因子内的题数一般最少包括3题的建议，将第四因子中的第19和20题删除．

最后，对余下的17个项目再次进行探索性因素分析，提取到3个因子，累积方差贡献率为65.008%，KMO值为0.949，Bartlett球形检验结果为p=0. 0 00＜0.001，达到显著水平，显示样本数据非常适合进行探索性因素分析，因素分析结果见表1．

根据各因素中各项目的意义，可以看出：因素1反映了教师的教学表征，将其命名为“教学表征”；因素2反映了教师鼓励学生参与课堂教学，将其命名为“鼓励学生参与”；因素3反映了教师了解学生和课程，并基于对学生和课程的了解进行教学，将其命名为“了解学生与课程”．

4.2 验证性因素分析

研究采用AMOS 7.0对392份中学生调查问卷的结果进行验证性因素分析．对4个分量表和总量表分别进行验证性因素分析，将各个分量表和总量表中所设置的观察变量构成样本的相关矩阵，作为模型检验的基础，均采用极大似然估计（maximum likelihood estimation）检验拟合程度．具体结果见表2．

从表2可以看出，总量表和各个分量表的RMSEA都小于0.1， 2 ＜χ2/df＜ 5；总量表和各个分量表的GFI、NFI、CFI和TLI都在0.9以上；这表明模型的拟合效果比较令人满意．图 1为中学生感知的数学教师学科教学知识结构模型．

4.3 信效度分析

4.3.1 信度分析

信度是测验可靠性和稳定性的指标．分别计算3个分测验与全量表的分半信度和内部一致性信度，结果见表3．检验结果表明，研究的测量工具信度达到评定要求．可以说，整个问卷作为测量中学生感知的数学教师学科教学知识的工具是可靠的．

4.3.2 效度分析

研究借鉴了张静仪等（1992）设计的问卷，并结合文献[1～34]所提出的PCK（或MPCK）的内涵和构成要素，针对鼓励学生参与、使用教学媒体、学科与课程、评价与了解学生和教学表征5个因素，结合数学学科的特征，广泛搜索并整理“PCK（或MPCK）的内涵和构成要素”条目，并向两位多年从事数学教学学科教学知识研究的学者和中学数学高级教师咨询，设计出“数学教师学科教学知识”问卷，保证了问卷具有良好的内容效度．

表1 中学生感知的数学教师学科教学知识的因素分析

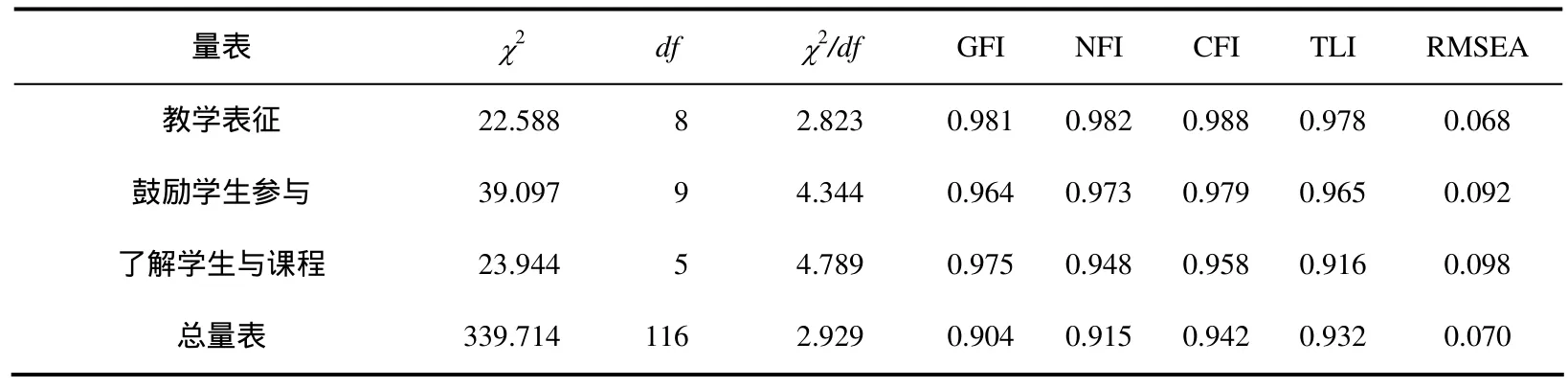
表2 模型的拟合指标

图1 中学生感知的数学教师学科教学知识结构模型

表3 中学生感知的数学教师学科教学知识的均值差异比较（n=783）

结构效度用来考察一个测验是否测量了先前的理论构思，评估测验的解释力．对中学生感知的数学教师学科教学知识问卷的探索性因素分析结果表明（表 1），量表结构清晰，各因子间相关介于0.630～0.699之间，达到显著水平，符合因素间相关的要求；项目的因素负荷都大于0.50，总方差解释率为65.008%，并且各项目含义都很清楚，可解释性强，这说明各维度的划分具有合理性．验证性因素分析结果也表明中学生感知的数学教师学科教学知识的结构模型是令人满意的模型．由此，可以认为中学生感知的数学教师学科教学知识调查表具有较好的结构效度．

验证量表效度的另一方式是比较各班级间在总量表与各分量表间是否有差异性，因此再进行变异数分析．变异数分析应符合观察体独立性、常态性、变异数同质性、可加性及球面性等假设．由项目分析结果显示该量表适合进行变异数分析．

表4呈现了F值与显著性p，总量表与各分量表在各班得分上均有显著差异（p<0.001）．由此可知，在不同班级的中学生所感受其数学教师的学科教学知识确有不同，也显示该量表确可经由学生观点来评量数学教师的学科教学知识．

4.4 中学生感知的数学教师学科教学知识的差异状况

对上述调查所得全部数据分学校类型、年级和性别，计算总量表和各个分量表的平均值与标准差，并进行多元方差分析，各种数据结果整理后见表5．

表5显示了不同类型学校、年级与性别的中学生在感知数学教师学科教学知识总量表及其各维度上的平均分与标准差．为比较不同类型学校、年级与性别的中学生在感知数学教师学科教学知识方面的差异，研究对中学生感知数学教师学科教学知识在学校类型、年级与性别两个变量上的差异进行复方差分析（MANOVA）（见表 5）．结果表明，在学校类型与年级变量上，中学生在感知数学教师学科教学知识3个维度上均表现出显著性差异，在性别变量上基本不存在显著性差异，学校与年级的交互效应上表现出显著性差异．

5 讨 论

（1）研究借鉴了张静仪等（1992）设计的问卷，并结合文献[1～34]所提出的PCK（或MPCK）的内涵和构成要素，针对鼓励学生参与、使用教学媒体、学科与课程、评价与了解学生和教学表征5个因素，结合数学学科的特征，广泛搜索并整理“PCK（或MPCK）的内涵和构成要素”条目，并向两位多年从事数学教学学科教学知识研究的学者和中学数学高级教师咨询，设计出“数学教师学科教学知识”问卷，说明问卷具有良好的内容效度．经SPSS统计软件进行项目分析和探索性因子分析，最后得到3个维度：即“教学表征”因子、“鼓励学生参与”因子和“了解学生与课程”因子．问卷各分量表Cronbachα系数介于0.721至0.912，分半信度介于0.592～0.892；问卷总量表Cronbachα系数为0.935，分半信度为0.873．探索性因素分析结果还表明，各分量表结构清晰，项目的因素负荷都大于 0.50，总方差解释率为65.008%，并且各项目含义都非常清楚，可解释性强．验证性因素分析结果表明中学生感知的数学教师学科教学知识的结构模型是令人满意的模型．由此，可以认为中学生感知的数学教师学科教学知识调查表具有较好的建构效度．

（2）验证性因素分析结果表明，总量表和各个分量表的RMSEA都小于 0.1， 2 ＜χ2/df＜ 5；总量表和各个分量表的GFI、NFI、CFI和TLI都在0.9以上；这表明模型的拟合效果比较令人满意，可以较好地验证探索性因素分析的理论构想．

（3）教师对自己教学的自我反思是教师PCK发展的重要因素之一[35]．因此，教师欲提升个人的 PCK，应随时反思自己的教学，就PCK的内涵做深度的分析反思．该量表则从学生角度感知教师之 PCK，教师可使用该量表收集学生的看法，作为中学数学教师对自我PCK反思的最具体可供参考的资料．

表4 17个班级的单因子变异数分析

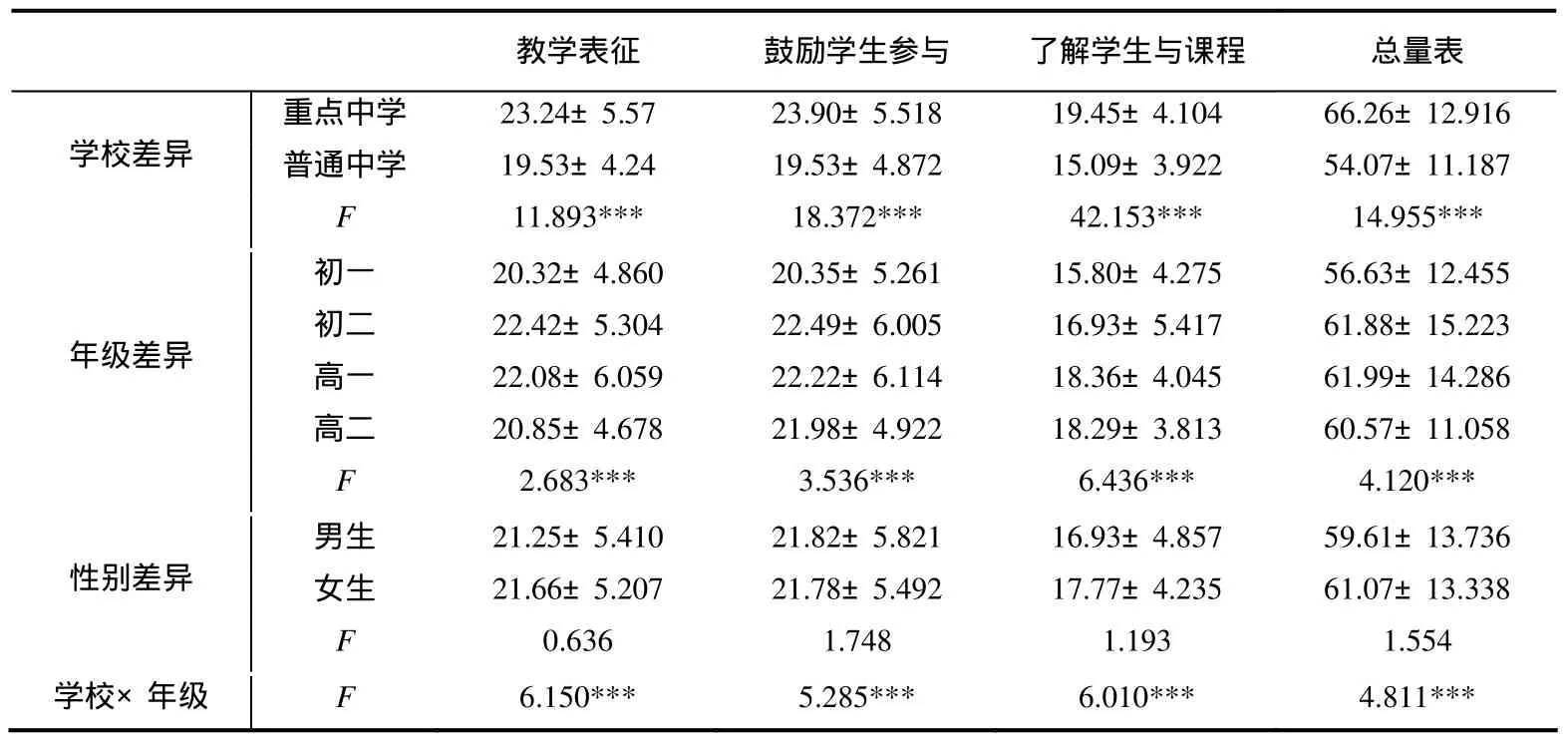
表5 中学生感知的数学教师学科教学知识的均值差异比较（n=783）

[1]Shulman L S. Those Who Understand: Knowledge Growth in Teaching [J]. Educational Researcher, 1986, 15(2): 4-14．

[2]Shulman L S. Knowledge and Teaching: Foundations of the New Reform [J]. Harvard Educational Review, 1987, 57(1):1-22.

[3]Tamir P. Subject Matter and Related Pedagogical Knowledge in Teacher Education [J]. Teaching and Teacher Education,1988, 4(2): 99-100.

[4]Smith D C, Neale D C. The Construction of Subject Matter Knowledge in Primary Science Teaching [J]. Teaching and Teacher Education, 1989, (5): 1-20.

[5]Marks R. Pedagogical Content Knowledge: from a Mathematical Case to a Modified Conception [J]. Journal of Teacher Education, 1990, 41(3): 3-11.

[6]Carter K. Teachers’ Knowledge and Learning to Teach [A]. In: W R Houston, M Haberman, J Kikula. Handbook of Research on Teacher Education [C]. Macmillan: New York, 1990.

[7]Grossman P. The Making of a Teacher: Teacher Knowledge and Teacher Education [M]. Teachers College Press,Columbia University, New York, NY, 1990.

[8]Gudmundsdottir S. The Narrative Nature of Pedagogical Content Knowledge [C]. Paper Presented at the Annual Meeting of the American Educational Research Association, Chicago, IL, 1991.

[9]Cochran K F, King R A, DeRuiter J A. Pedagogical Content Knowledge: A Tentative Model for Teacher Preparation [C].Paper Presented at the Annual Meeting of the American Educational Research Association, Chicago, IL, 1991.

[10]Magnusson S, Borko H, Krajcik J. Teaching Complex Subject Matter in Science: Insight from an Analysis of Pedagogical Content Knowledge [C]. Paper Presented at the Annual Meeting of the National Association for Research in Science Teaching, Anaheim, CA, 1994.

[11]Fernandez-Balboa J M, Stiehl J. The Generic Nature of Pedagogical Content Knowledge Among College Professors [J].Teaching and Teacher Education, 1995, 11(3): 293-306.

[12]Van Driel J, Verloop N, De Vos W. Developing Science Teachers’ Pedagogical Content Knowledge [J]. Journal of Research in Science Teaching, 1998, 35(6): 673-695.

[13]de Berg K C, Greive C. Understanding the Siphon: an Example of the Development of Pedagogical Content Knowledge Using Textbooks and the Writings of Early Scientists [J]. Australian Science Teachers’ Journal, 1999, 45(4): 19-26.

[14]Magnusson S, Krajcik J, Borko H. Nature, Sources, and Development of Pedagogical Content Knowledge for Science[A]. In: J Gess-Newsome, N G Lederman. Examining Pedagogical Content Knowledge [C]. Dordrecht, Netherlands:Kluwer, 1999.

[15]Carlsen W S. Domains of Teacher Knowledge [A]. In: J Gess-Newsome, N G Lederman. Examining Pedagogical Content Knowledge: the Construct and Its Implications for Science Education [C]. Dordrecht, the Netherlands: Kluwer Academic Publishers, 1999.

[16]W R Veal, J G Makinster. Pedagogical Content Knowledge Taxonomies [EB/OL]. http://unr.edu/homepage/crowther/ejse/vealmak.html.

[17]Barrett D, Green K. Pedagogical Content Knowledge as a Foundation for an Interdisciplinary Graduate Program [J].Science Educator, 2009, 18(1): 60.

[18]An S, Kulm G, Wu Z. The Pedagogical Content Knowledge of Middle School Mathematics Teachers in China and the U.S [J]. Journal of Mathematics Teacher Education, 2004, (7): 145-172.

[19]田宏根，杨军．从一节课管窥高中数学教师教学知识的发展[J]．数学教育学报，2007，16（2）：51-53．

[20]Ball D, Thames M, Phelps G. Content Knowledge for Teaching: What Makes It Special [J]. Journal of Teacher Education,2008, (59): 389-407.

[21]景敏．在职教师教学内容知识发展研究[M]．桂林：广西师范大学出版社，2008．

[22]黄毅英，许世红．数学教学内容知识——结构特征与研发举例[J]．数学教育学报，2009，18（1）：5-9．

[23]童莉．数学教师专业发展的新视角——数学教学内容知识（MPCK）[J]．数学教育学报，2010，19（2）：24．

[24]董涛．数学课堂中PCK的结构[J]．内蒙古师范大学学报（教育科学版），2010，（8）：122-124．

[25]梅松竹，冷平，王燕荣．数学教师MPCK之案例剖析[J]．中学数学杂志，2010，（11）：10-12．

[26]李渺，宁连华．数学教学内容知识（MPCK）的构成成分表现形式及其意义[J]．数学教育学报，2011，20（2）：12．

[27]Loughran J, Gunstone R, Berry A, et al. Science Cases in Action: Developing an Understanding of Science Teachers’Pedagogical Content Knowledge [C]. Paper Presented at the Annual Meeting of the National Association for Research in Science Teaching, New Orleans, LA, 2000.

[28]Brophy J, Good T L. Teacher Behavior and Student Achievement [A]. In: M C Wittrock. Handbook of Research on Teaching: Third Edition [C]. New York: Macmillan, 1986.

[29]Kennedy M M. Education Reform and Subject Knowledge [J]. Journal of Research in Science Teaching, 1998, 35(3):249-263.

[30]Farser B J. Classroom Environment [M]. London: Croom Hlem, 1986.

[31]Baxter J A, Lederman N G. Assessment and Measurement of Pedagogical Content Knowledge [A]. In: J Gess-Newsome,N G Lederman. Examining Pedagogical Content Knowledge [C]. Dordrecht, Netherlands: Kluwer, 1999.

[32]段晓林，王国华，张惠博．学生对教师之学科教学知觉问卷之发展[J]．科学教育学刊，1998，（2）：129-147．

[33]王国华，段晓林，张惠博．国中学生对科学教师学科教学之知觉[J]．科学教育学刊，1998，（4）：363-381．

[34]张静仪，戴翠华．“国小学童感知自然老师PCK量表”之效化研究[J]．台北师范学院学报，1992，（2）：187-212．

[35]Gess-Newsome J, Lederman N G. Preservice Biological Teachers’ Knowledge Structures as a Function of Professional Teacher Education: a Year-long Assessment [J]. Science Teacher Education, 1993, 77(1): 25-43.