一元线性回归模型的参数估计法的误差分析
唐薇,冯长焕
(西华师范大学数学与信息学院,四川南充637002)
一元线性回归模型的参数估计法的误差分析
唐薇,冯长焕
(西华师范大学数学与信息学院,四川南充637002)
对横向距离平方和最小法与最小二乘法的误差进行分析,发现二者的误差大小与拟合直线的斜率有关.这两种方法的参数估计表达式与最小距离平方和法的参数估计表达式有相应的关系.通过举例比较和讨论了这三种数据拟合方法的优劣,并分别给出了较合理的应用控制条件.
参数估计;横向距离平方和最小法;最小二乘法;回归分析
数据拟合的原理是:给定一组观测数据(或散点等)(xi,yi)(i=1,2,3,…,m),在某一类曲线中寻找一条最佳曲线y=φ(x),使该曲线拟合这些数据,曲线的选取要靠经验和对数据的直观分析,因此有时称为经验公式,最佳的标准是使总体误差最小.如果采用绝对误差,数学上采用微积分知识求最小值不容易处理,因此通常采用最小二乘法来处理[1].
横向距离平方和最小法跟最小二乘法一样是一种将距离简化处理的方法,它们分别采用横向(x向)和纵向(y向)离差代替综合离差(x向和y向),降低了运算的复杂程度,但同时带来了一定的误差.
1 两种方法的误差分析
1.1 两种方法的参数估计准则
最小二乘法是给出一条直线,使得每个样本点离这条直线的纵向距离的平方和达到最小[2].其纵向距离平方和为
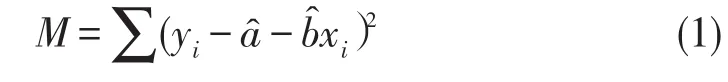
从式(1)可以看出最小二乘法属于单方向(纵轴y向)的数据拟合,即用表示待拟合点(xi,yi)到拟合直线的距离.显然di纵不是点到直线的垂直距离(最小距离),因为它只是单方向(y向)拟合.最小二乘法所得参数a,b的估计值为:

横向距离平方和最小法是给出一条直线,使得每个点离这条直线的横向距离的平方和达到最小[3].令横向距离平方和为

从式(2)可以看出横向距离平方和最小法属于单方向(横轴x向)的数据拟合,即用表示待拟合点(xi,yi)到拟合直线的横向距离.同样di横不是点到直线的垂直距离(最小距离),因为它只是单方向(x向)拟合.横向距离平方和最小法的参数a,b的估计值为:

1.2 图形分析两种方法的误差
现通过图示来进一步分析前两种简化处理的方法和全最小二乘法的差别.如图1,设拟合的曲线为y=aˆ+bˆx,其与x正方向的夹角为α,则有tanα=b.过任一待拟合点(xi,yi)分别作出其到拟合直线的最小距离di、纵向距离di纵、横向距离di横.显然存在几何关系di=di纵cosα=di横sinα.令

当||b=1时,Δ纵=Δ横,最小二乘法和横向距离平方和法的误差相等,两种方法求得的拟合直线相同.当||b>1时,Δ横<Δ纵,应采用横向距离平方和最小法精确度更高.当||b<1时,Δ纵<Δ横,应采用最小二乘法精确度更高.

图1 横向距离平方和最小法与最小二乘法的差别
虽然这两种方法有一定的拟合误差,但它们是一种十分重要的简化处理手段.最小二乘法是假设自变量没有观测误差,横向距离平方和最小法是假设因变量没有观测误差.从误差分析来看,最小距离平方和法即全最小二乘法可以改善这些问题.为所有样本点(xi,yi)到直线y=a+bx的垂直距离的平方,因为,所以使上述(1)式和(2)式的和M+N达到最小即是使样本点到直线的垂直距离的平方和最小,即:
通过这次活动,山西省孝义市中和路小学将遵从传统仪规,以礼乐致敬先贤,吟诵经典,传承礼仪,在中和这片沃土上,人人争做“中允明德,和协至善”的好少年!
设(xi,yi)到拟合直线的距离为di,则使

为全最小二乘法的准则.当模型中难以区分因变量和自变量时,即所有变量都有不可忽略的误差时,使用经典的最小二乘法已经不再合适.这就需要使用考虑了所有变量误差的全最小二乘法.与经典最小二乘法相比全最小二乘法得到回归参数与真实模型参数更为接近[4].
对b求偏导,得:


一个表达式与横向距离平方和法求得的一致,另一个表达式与最小二乘法求得的拟合直线是互相垂直的关系,说明最小距离平方和法的斜率参数应小于或等于横向距离平方和法的斜率参数.
最小距离平方和法的斜率参数的选择可根据拟合结果y倚x是正相关还是负相关.计算线性回归分析中的相关系数,当r>0则选择,当r<0则
2 三种参数估计方法的应用控制条件
运用国家统计局公布的关于中国1994-2004年旅游年总收入数据,自变量t是年份序号,因变量y是旅游总收入,建立一元线性回归模型(表1).
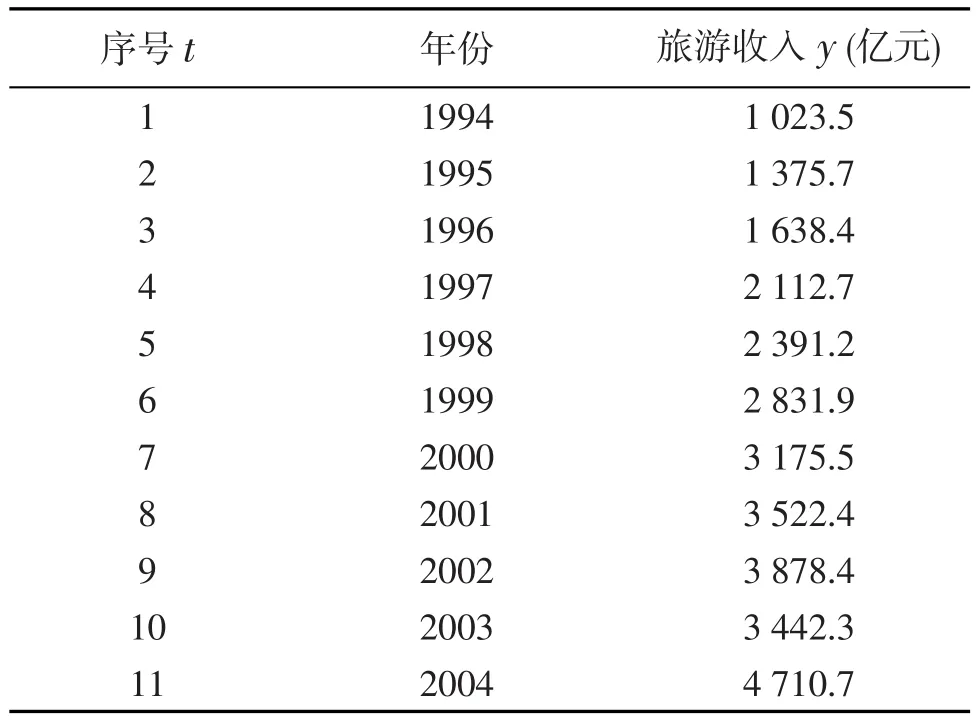
表1 1994-2004年我国旅游年总收入Table1 1994-2004 annualgross incomeof tourism
根据最小二乘法、横向距离平方和最小法、最小一乘法、全最小一乘法四种方法的原理,利用SPSS和LINGO软件建立的一元线性回归方程分别为:

利用全最小二乘法得到的回归方程为:

前四种方法的残差平方和分别为556 366.8、112 376.6、658 827.6、659 987.4,而全最小二乘法的残差平方和仅为34 748.42,表明全最小二乘法更符合实际,它的参数估计精度较高.但不能忽略横向距离平方和最小法在大斜率时拟合效果好且容易求解的优势.
为检验各种方法的稳健性,采用前后均值法把2003年的旅游收入用2002年与2004年的数据的平均值4 294.535取代,并假设是在不受异常点影响下建立的模型.通过SPSS和LINGO软件重新根据四种方法的原理对模型的参数进行估计,获得的公式分别为[3]:

此时利用全最小二乘法得到的回归方程为:

稳健性是指当个别点变化时,最优直线也发生变化,其强弱由参数相对变化率反映[6].参数的相对变化率越小,说明此种方法的稳健性越好.表2给出了不同方法下参数的变化率.

表2 不同方法下参数的变化率[3]Table2 The rateofparameters changeunder differentmethod
通过比较可以发现全最小二乘法参数b的稳健性很好,参数a的稳健性不好.因为ˉ,异常值处理方法不当使得差异很大,引起参数a的稳健性不好.但该方法的稳健性高于最小二乘法.
全最小二乘法考虑的是综合离差,该方法所得直线方程不会因为坐标系选取的不同而改变.尽管全最小二乘法可减少数据拟合的误差.但不能忽略横向距离平方和最小法在大斜率时拟合效果好且容易求解的优势.
4 结论
为了兼顾各种方法的优点,根据它们的应用控制条件,得到如下结论:
(3)全最小二乘拟合精度高但计算较为麻烦,并且它的解不适合作预报[8].前两种方法求解的方程为回归方程,并非相关方程,原因是它要求相关的两个变量一个为因变量一个为自变量,且假设其中一个变量没有观测误差.前两种方法带来的误差并不能保证双向(x向和y向)同时相关,所以在求解相关方程时只有采用全最小二乘法才能得到满意的相关关系.
[1]周浩.线性时间拟合方法的误差分析及其改进应用[J].大学数学,2013(1):70-76.
[2]曹昭.一元线性回归中的相关系数与回归直线斜率探讨[J].统计与决策,2009(9):147-148.
[3]唐薇,冯长焕.参数估计的新方法——横向距离平方和最小法[J].绵阳师范学院学报,2013(8):9-14.
[4]王福昌,曹慧荣,朱红霞.经典最小二乘与全最小二乘法及其参数估计[J].统计与决策,2009(1):16-17.
[5]WuW L,Zhang Y,Fu ZQ,etal.A new leastsquaremethod on linear fitting[J].Scientific Journalof Electrical Engineering,2013,3(1): 8-12.
[6]杨桂元.最小一乘法在建立预测模型中的应用[J].江苏统计, 1998,(5):17-19.
[7]杨述武,赵立竹,沈国土.普通物理实验(力学及热学部分)[M].第4版.北京:高等教育出版社,2007.
[8]张洪俄,黄劲东,范文雷.全最小二乘法及其在参数估计中的应用[J].1995(1):40-47.
【编校:许洁】
Error Analysisof Parameter Estimating Method in Single Variable Linear Regression
TANGWei,FENGChanghuan
(CollegeofMathematicsand Information,ChinaWestNormalUniversity,Nanchong,Sichuan 637002,China)
Theminimum sum of lateraldistance square and the leastsquaremethod were analyzed,finding that theirerror are related to the slope of the fitted line and that the parameter estimating expression of the twomethods are associated with the expression of the least distance squaremethod.Through comparison,the advantages and disadvantages of the threemethodswere discussed and reasonableapplication control conditionsweregiven.
parameter estimation;theminimum sum of lateral distance square;the leastsquaremethod;regression analysis
O212.1
A
1671-5365(2014)12-0018-04
2014-05-27修回:2014-07-09
唐薇(1989-),女,硕士研究生,研究方向为统计学理论及应用
冯长焕(1972-),女,教授,硕士生导师,研究方向为统计学理论及应用
时间:2014-07-11 09:33
http://www.cnki.net/kcms/detail/51.1630.Z.20140711.0933.002.htm l

