等式约束条件极值存在的必要条件及其应用

唐军强

（焦作大学基础部，河南焦作454000）

等式约束条件极值存在的必要条件及其应用

唐军强

（焦作大学基础部，河南焦作454000）

从拉格朗日乘子法出发，考虑多元函数在等式约束条件下的极值问题.由线性方程组理论得到多元函数在一个或多个等式约束条件下极值点存在的必要条件.并进一步考虑该条件在优化理论中的应用，通过将不等式约束转化为等式约束，运用等约束条件下极值存在的必要条件获得最优解.

多元函数；条件极值；拉格朗日乘子法；驻点；梯度；最优解

关于拉格朗日乘子法求解多元函数等式约束下的极值问题，目前有两个研究方向：一个是如果有驻点的话，如何求得驻点坐标；另一个是如何判断所得的驻点是否是极值点，是极大值还是极小值.分别称其为极值存在的必要条件和充分条件.充分性条件的论证比较多[1-3]；必要性的研究相对较少，原因是拉格朗日乘子法本身就是用来求驻点坐标的.但是拉格朗日乘子法求解该类问题时，经常需要求解一个多元的线性或者非线性方程组，这并不容易.本文从拉格朗日乘子法出发，在文献[4]、[5]的基础上，由线性方程组理论推导出n维空间中等式约束条件下极值存在的必要条件.该条件形式更加简单，可以简化求解一个多元方程组的困难.进一步考虑该条件在优化理论中的应用，通过将不等式约束转化为等式约束，运用等式约束下条件极值存在的必要条件获得最优解.

1 必要条件的推出

1.1三维空间中一个等式约束条件下的极值问题

考虑函数u=f(x,y,z)在条件φ(x,y,z)=0下的极值问题.由拉格朗日乘子法，构造拉格朗日函数L=f(x,y,z)+λφ(x,y,z)，并分别求导得到

通过求解λ并将其代入前三个式子，得到

其实（2）式中的前三个式子就相当于下式

1.2三维空间中两个等式约束条件下的极值问题

考虑函数u=f(x,y,z)在条件φ1(x,y,z)=0、φ2(x,y,z)=0下的极值问题.由拉格朗日乘子法，构造拉格朗日函数L=f(x,y,z)+λ1φ1(x,y,z)+λ2φ2(x,y,z),并分别求导得到

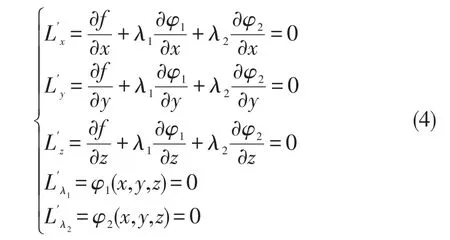
将（4）式中的前三个式子改写为

将λ1、λ2看作未知量，由线性方程组理论可知，其有非零解的必要条件是

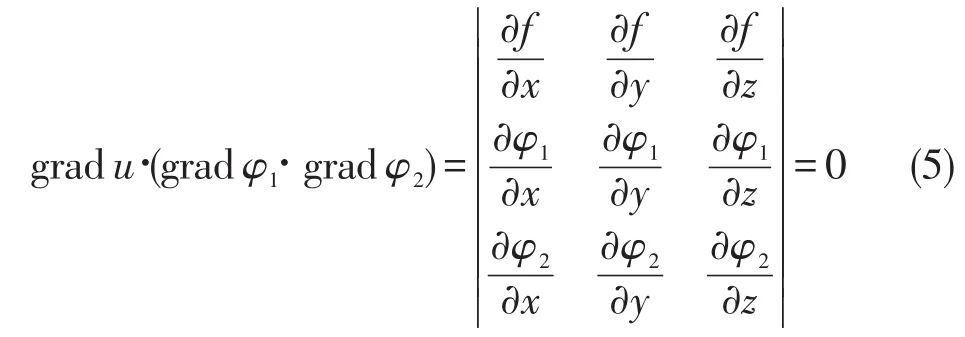
（5）式是三个梯度向量的混合积.从这里可以看出，结论与1.1相似.由此得到启发：可以抛开拉格朗日函数，仅仅考虑（3）式或（5）式构成的方程，通过求解该方程得到驻点的各个分量坐标之间的关系，然后再结合条件函数，就可以求得驻点的坐标.

1.3 n(n＞3)维空间中多个等式约束条件下的极值问题

将该问题进一步推广，考虑n元函数u=f(x1, x2,…,xn)在条件φ1(x1,x2,…,xn)=0，φ2(x1,x2,…, xn)=0,…φk(x1,x2,…,xn)=0(k≤n-1)下的极值问题.构造拉格朗日函数L=f+λ1φ1+λ2φ2+…+ λkφk,并对其求导得到

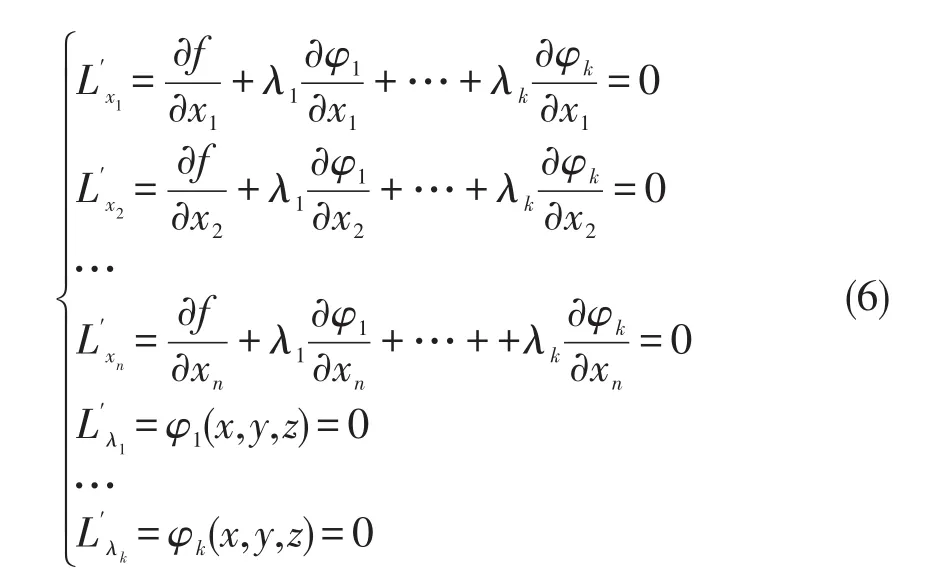
将（6）式中的前n个式子改写为

当k=n-1时，（7）式左端矩阵为方阵，其有非零解的必要条件是值问题.即3y2-4z=0.算出f和φ的梯度向量构造矩阵如下

当k＜n-1时，（7）式左端矩阵不是方阵，如果它有一个k+1阶子阵行列式不为0，是不可能存在非零解的，从而其有非零解的必要条件是：其所有k+1阶子阵行列式均为0.在求解过程中，可以任取其k+1阶的子阵并令其行列式为0，驻点坐标只能是它们的交集.下面举例说明.

例1：求曲面4z=3x2-2xy+3y2到平面x+y-4z=1的最短距离.

解：由点到平面的距离公式，将其转化为条件极

由1.3的结论，上式存在非零解的必要条件为：左端矩阵任意2阶子阵行列式为0.即

分别解之得x=y,6x-2y=1,6y-2x=1.从而应有，代入φ解得，最短距离为.

2 在优化理论中的应用

2.1一般非线性规划的最优性

非线性规划，即目标函数或者条件函数中出现有非线性等式或不等式的优化问题.现考虑

其中φi(1≤i≤ki),ψj(1≤j≤kj)关于x1,x2,…,xn均具有一阶连续偏导数.假设x*=(,,…,为（8）式的最优解.为了尽可能将该问题叙述清楚，先列举出所有可能取到最优解的点：

（I）∇f=0的点；

（II）目标函数f的不可导点；

（III）用1.3的结论算出的驻点；

（IV）可行域所在的凸多边形的顶点；

（V）无穷远点.

可以看到（I）、（II）中的点只和f有关.除了（IV）之外，其他的点都需要验证是否在可行域中.（V）一般只起到和其他点进行比较和判定的作用.若无穷远点在可行域中且使得f→+∞，则最优解应该在其他类型的点中取到；若f→-∞则该问题无最优解.下面再分情况进行讨论：

ⅰ)若（8）式只有等式约束，则等式约束的个数不会多于自变量的个数.一般情况下，（I）、（I）中的点不会满足所有的等式约束.需要着重考虑（III）和（IV）中的点.

ⅱ)若（8）式同时具有等式约束和不等式约束，x*首先应该满足等式约束条件ψj=0，从而应当先用1.3求等式约束下的驻点，然后验证所得的驻点坐标是否满足其余的不等式约束条件φi≥0.

ⅲ)若（8）式只有不等式约束，至少有一个不等式约束对x*是有效约束，即存在一个1≤m≤ki，使φm(x*)=0，从而可以将其转化为等式约束求解[6]，然后再验证所得的解是否满足其余的不等式即可.下面举例说明.

例2：考虑如下线性规划问题[7]：

解：可知（I）、（II）中的点不存在.然后考虑（III），先考虑等式约束，算出f和φ1,φ2,φ3的梯度向量构造矩阵如下

计算可知，上面矩阵中没有一个4阶的子阵行列式为0，从而不存在非零解.由1.3的结论，（III）中的点也不存在.如果没有x1,x2,x3,x4,x5≥0的限制，该问题是没有极值的.将其转化为下面包含不等式约束的优化问题：

可以看出，无穷远点不在其可行域中，如果该问题存在最优解，只能在（IV）中取到.令前三个不等式约束为等式约束，分别求出他们两两之间的交点(x2,x3)坐标为可知满足题设条件的只有(,)，代入φ,φ,φ，求出原问题123的最优解为

从例2可以看到，线性规划中，（III）中的点是不存在的.因为线性规划的目标函数的图象都是直线或者平面，不存在驻点的问题.在只考虑等式约束的情况下，例2如果用拉格朗日乘子法组成方程组求解，就会得到矛盾的结果，这在文献[7]中已经得到验证.这也从另一个方面解释了为什么有时候用拉格朗日乘子法求解线性规划问题时会失效.

需要指出的是，对于同时具有等式约束和不等式约束的情况，用1.3中的方法，即使找到一个点x*=(,,∙∙∙,)满足所有的等式约束，且使得φi(x*)≥0,1≤i≤ki，仍不能确定其就是最优解.而必须将所有此类点找出来，代入目标函数，比较大小来确定.例如：

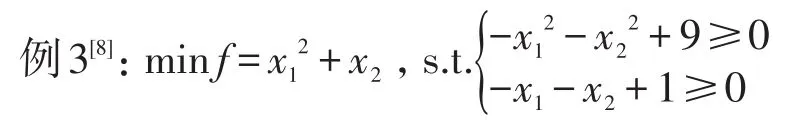
解：∇f=0无解，（I）、（II）中的点不存在.无穷远点也不在其可行域中.从而其最优解要么在--+9=0上取到，要么在-x1-x2+1=0上取到.可以将其转化为下面两个规划问题

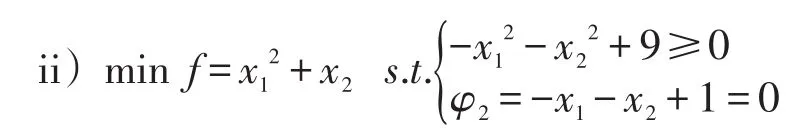
综合以上，将三个点的坐标代入f，并比较大小，得出最优解为(0,-3).

2.2求解二次规划问题

二次规划是约束为线性而目标函数是二次函数的最优化问题.

例4：求解二次规划

解：令∇f=(x1-1,x2-2)=0，解得(x1,x2)=(1,2)，该点不在可行域中.从而（I）、（II）中的点不存在.无穷远点在可行域中，但是使得f→+∞.再考虑（III），与例3同样的方法，将其转化为两个规划问题:

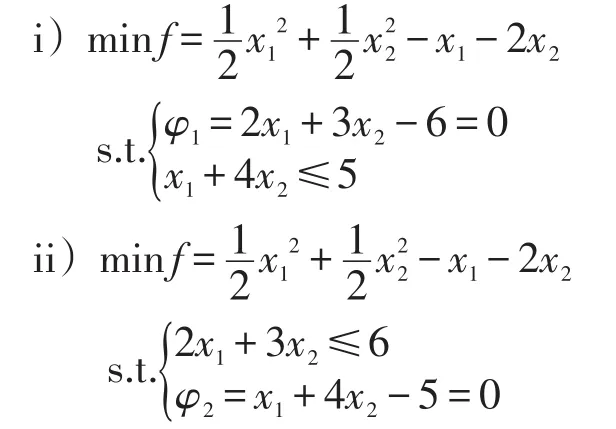
解得4x1-x2-2=0，联立φ2，得方程组：

3 结语

1.1－1.3为等式约束下的条件极值问题提供了一条捷径，就相当于求一元可导函数的驻点坐标时只需要f′(x)=0一样简单，不过该条件并非充分条件.且对于非线性规划，会遇到两个方面的困难：

1）当不等式约束的个数比较多的时候，要确定哪一个不等式对最优解x*而言是有效约束，不是一件容易的事情.只能逐个的去寻找并比较大小.

2）即使对于都是等式约束的问题，当目标函数和约束条件次数比较高或者包含有非幂函数的时候，用1.3求解一个多元高次或者非幂函数构成的非线性方程本身就成为一个问题.

［1］杨斌，干晓蓉.等约束条件下多元函数条件极值的充分条件[J].云南师范大学学报,2012(2):47-52.

［2］宋宜美.关于条件极值的两点思考[J].高等数学研究,2011(14): 107-109.

［3］潘武敏.高等数学中多元函数条件极值的充分性研究[J].科技信息,2007(25):202-203.

［4］张秀梅.三元函数双条件极值的一个必要条件[J].辽宁工业大学学报,2012(2):138-140.

［5］唐军强.用方向导数法求解多元函数条件极值[J].科技创新导报,2008(15):179-180.

［6］戎海武.关于拉格朗日乘数法的两点思考[J].高等数学研究, 2013(4):81-82.

［7］陈敬华.拉格朗日乘子法及其推广[J].湖北师范学院学报,2010 (4):108-111.

［8］施光燕,董加礼.最优化方法[M].北京:高等教育出版社,2003.

【编校：许洁】

Necessary Condition for Conditional Extrem e Values under Equality Constrains and App lication in the Theory of Optim ization

TANG Junqiang
(DepartmentofBasic Course,Jiaozuo College,Jiaozuo,Henan 454000,China)

The conditional extreme values formultivariable functions under equality constrainswas investigated by starting from themethod of Lagrangemultipliers.The necessary condition for the existence of conditional extreme valueswas obtained by theory of linear equations.Itsapplication in the theory ofoptimization was discussed.The optimal solution is obtained with thisnecessary condition by converting inequality constrains into equality constrains.

multivariable function;conditionalextreme;Lagrangemultiplier;stagnation point;gradient;optimalsolution

O172

A

1671-5365(2014)12-0014-04

2014-09-09修回：2014-10-02

唐军强（1980-），男，讲师，硕士，研究方向为应用泛函分析

时间：2014-10-15 12:59

http://www.cnki.net/kcms/detail/51.1630.Z.20141015.1337.003.htm l