单测角相对导航的相对距离重构新算法
龚柏春 ,罗建军 ,马 悦
(1.西北工业大学 航天学院,西安 710072;2.航天飞行动力学技术重点实验室,西安 710072;3.96271部队,洛阳 471600)
单测角相对导航的相对距离重构新算法
龚柏春1,2,罗建军1,2,马 悦3
(1.西北工业大学 航天学院,西安 710072;2.航天飞行动力学技术重点实验室,西安 710072;3.96271部队,洛阳 471600)
针对空间非合作目标中远程交会的单测角相对导航技术中核心的相对距离重构问题,首次提出了一种基于初值辅助的CCD相对测角/GPS绝对定位的相对距离重构新算法。首先在分析传统重构方法数学本质和优缺点的基础上,以余弦定理为基础,结合GPS历元差分建立了相对距离重构算法模型,然后对该算法的重构误差进行了理论推导和仿真分析。最后对两种工况下相对距离的重构进行了数值仿真。仿真结果表明该算法能够较为精确的重构出相对距离,重构精度取决于辅助初值的精度。因此,该算法具有重要的研究意义和应用价值。
空间非合作目标;相对导航;单测角;相对距离
近年来,针对地球轨道资源日趋紧张、故障卫星在轨修复以及轨道碎片清理等问题,各国积极展开了利用空间机器人(服务星)对故障卫星、轨道碎片等空间非合作目标进行监视、接近以及捕获等在轨服务技术研究[1-2]。相对导航则是实现在轨自主服务的关键使能技术之一。通常服务星需要诸如微波雷达、激光雷达等星载传感器系统来自主测量非合作目标的相对运动信息,但是由于体积、质量和燃耗等因素,这类主动式有源传感器是不能适应未来服务星微小型化发展趋势的。相反的,CCD相机这类被动式无源传感器在这些方面却体现出了相当的潜在优势。但是,在中远程交会阶段,CCD相机仅能测量出服务星相对于非合作目标的相对视线信息,而没有直接的距离信息[3]。正是由于缺乏距离信息,会导致相对导航滤波系统不完全可观测。因此,研究仅有视线角信息的相对导航技术具有重要的理论研究意义和工程应用价值,而相对距离重构算法更是单测角相对导航的算法的核心。
国内外众多学者对相对距离重构算法进行了研究,基本上都是基于“角-边-角”的三角形确定算法完成相对距离重构的。Geller、Woffinden[3-5]等首先提出了如图1所示的利用服务星轨道机动操作进行相对距离重构的思想,该算法通过非视线方向轨道机动获取“边长”δr,从而由δr、角α和角β确定三角形的外形,即确定相对距离ρ。Li[6]在 Geller等人研究的基础上深入研究了轨道机动策略的优化问题。
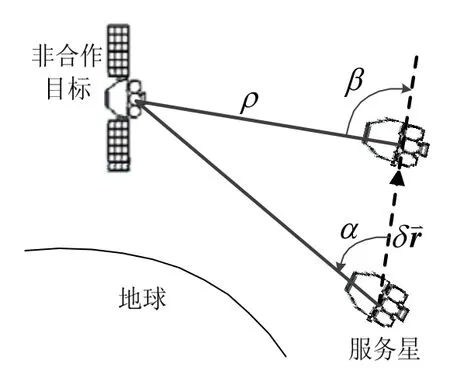
图1 轨道机动法和双星编队法Fig.1 Methods of orbit maneuvering and satellites formation
刘光明[7]、苏建敏[8]等研究了基于双星编队联合测量的相对距离重构算法,此类算法是通过双星编队获取的测量基线和双星对目标器的视线角确定三角形的外形,从而重构出相对距离ρ,其示意图同图1。同样,Chen、Wang等[9-10]也研究了利用主星和辅助卫星进行联合测量的重构技术。
Woffinden[11]提出了利用服务星进行姿态机动变换光学相机的位置获取测量基线,同时以两组视线角重构相对距离的算法。Crassidis、Kim等[12-13]分别研究了基于标志点检测、多敏感器的相对距离重构算法,此类算法原理类似于姿态机动法,但是省略的姿态机动过程。
尽管上述算法可以实现单测角相对导航中的相对距离重构,但是它们都有各自的局限性和使用范围。轨道机动法因为需要服务星进行特殊的机动而会对卫星的安全性和燃料消耗产生重要影响[5-6],并且需要服务星经常性地进行机动产生δr,否则不能完成相对距离重构。同时,沿视线接近时算法失效,因此不能适合中远程接近等耗时较长的情况;双星编队方法则需要动用两颗卫星或者需要主星释放伴飞小卫星,这在实际中不易实现且代价较大,且双星观测矢量夹角越小估计精度越低,两观测矢量平行时距离估计失效[7];姿态机动法或多敏感器法只适用于距离较近的情况,当处于中远距离时“基线”太短,获得的多视线几乎平行或者只有单视线,算法失效。
因此,本文针对单服务星对空间非合作目标中远程交会的单测角相对导航问题,从“边-角-边”三角形确定原理的角度出发,提出一种基于初值辅助的CCD相对测角/GPS绝对定位的相对距离重构新算法。下文中首先详细阐述相对距离重构算法的几何模型构建,然后对该重构算法的误差进行理论推导与仿真分析,最后对该算法进行两种工况的数值仿真与分析。
1 相对距离重构模型
当非合作目标器飞临地基/天基测量弧段内时,由地基/天基测量出非合作目标器某一时刻的惯性位置,而服务星则由星载的 GPS给出其同一时刻的惯性位置,这样就可以确定出两飞行器之间的相对距离初值。确定初值后不再需要地面测量的辅助,之后的相对距离由GPS导航历元差分的几何递推来估计,如图2所示。这里将服务星对目标器的接近运动分为两类:一类是沿视线方向接近,如图2中的方向;一类是非视线方向接近,方向。
对于沿视线方向运动,相对距离的递推公式为

对于非视线方向接近,可由三角形确定规则来估计相对距离。如图2中的三角形,已知三角形的边长和其夹角α就可以根据“边-角-边”规则确定三角形的形状,即可由余弦定理确定的边长,其计算公式为:
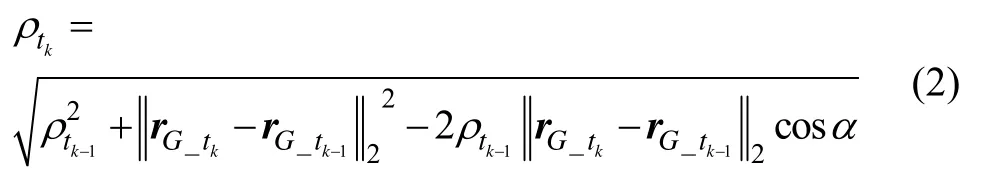
式中,α是tk-1时刻的单位视线矢量i与服务星自身单位位移矢量δr的夹角,可以如下计算:
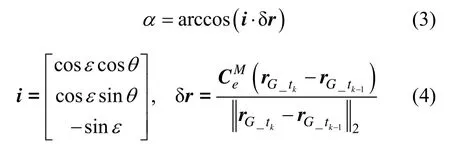
式中,ε、θ分别是视线仰角和视线偏角,是GPS在WGS-84地固联系e到服务星CCD光学测量坐标系M的变换矩阵。可以分解为:


图2 相对距离估计几何示意图Fig.2 Geometrical diagram of estimated relative distance
由式(2)可知,当α等于0时,式(2)等价于式(1),这样就把视线方向和非视线方向接近这两种情况下的相对距离递推统一起来了,不论由哪种方向接近都可以由式(2)进行相对距离的实时递推重构了。
将式(3)(4)和(5)带入式(2)并化简可得:

因此,无论服务星进行何种机动,相对距离都可由式(6)进行递推重构了。
2 重构误差分析
由式(2)可知,与重构有关的序列变量是r和ρ,而这两者分别与GPS和递推几何关系有关,因此下面重点分析与这两类因素有关的误差。
2.1 GPS历元差分误差分析
GPS导航的主要误差源有卫星星历误差、卫星钟差、信号传播误差以及接收机测量误差等,其位置误差δrG的相关性可用一阶马尔科夫过程表示[14]:
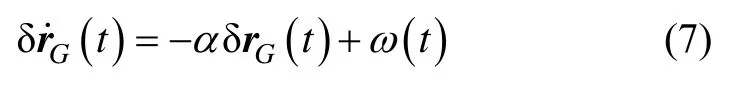
式中,α为反相关时间常数,ω为零均值的高斯白噪声。利用解析法对式(7)进行离散化可得:
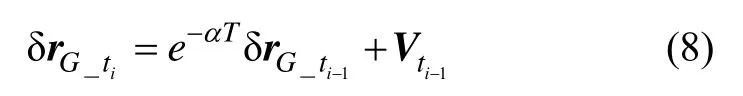
式中,Vti为零均值高斯白噪声序列,T为离散化步长。因此:
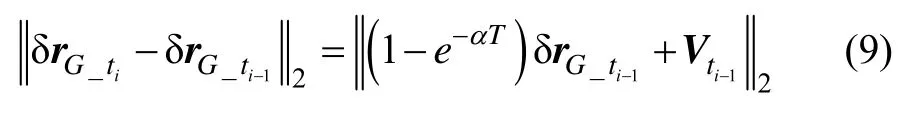
所以,相邻时刻误差源对定位的影响变化缓慢,因此,通过历元差分可以消除大部分的误差。
2.2 递推几何误差分析
根据角α的定义可知,,从而,代入式(2)可得:

式中,当α=0时,即沿视线接近时,左等号成立;当α=π时,即沿视线撤离时右等号成立。因此,通过不等式关系传递可得:
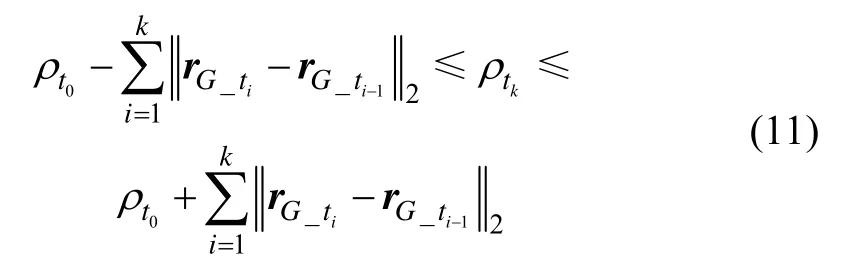
令带上标“~”的参量表示测计值,不带上标的为真实值,则:
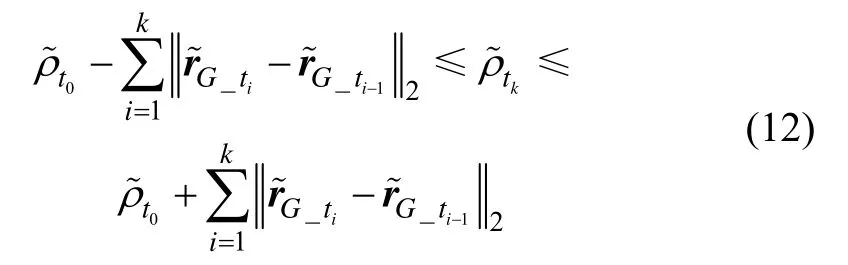
而测算值可表示为真实值加误差的情况,即:
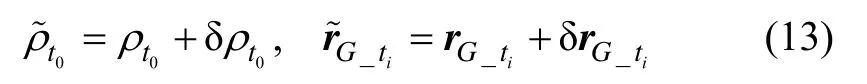
将式(13)代入式(12)可得:
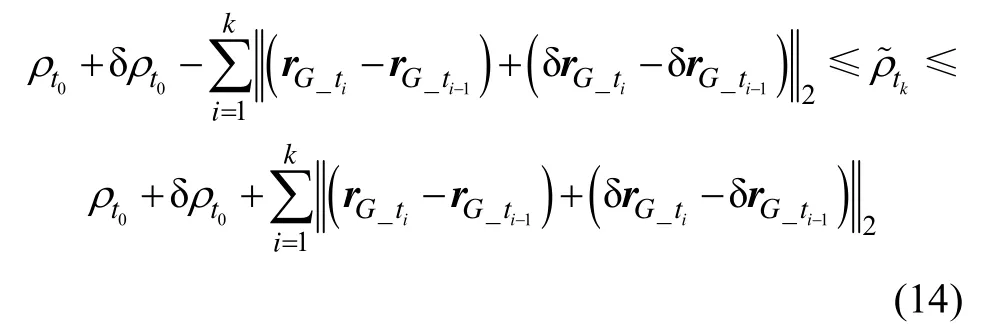
根据向量范数三公理中的三角不等式公理可知:

将式(11) (15)代入式(14)可得:
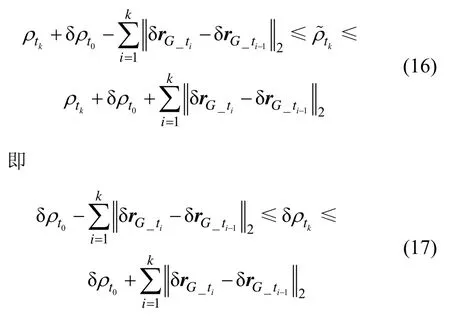
由式(17)可知,第k次重构误差的上下限只与初值辅助误差和GPS绝对定位历元差分误差有关,并且该上下限是随时间变大的,变化速度仅与绝对定位误差有关。同时,由前述分析可知,当服务器沿视线方向机动时相对距离重构误差最大。
3 仿真分析
为了充分考究所提算法的有效性、误差特性以及鲁棒性等相关性能,这里进行两组仿真,第一组对重构误差本身进行仿真分析,并与传统重构方法进行对比,第二组对不同辅助初值下的重构进行仿真。
3.1 重构误差仿真分析
为了对误差的上下限发散速度进行评估,进行了数值仿真。假设GPS初始位置圆误差为20 m,则可令。同时,根据工程经验可假设误差的相关时间为 10 s,即反相关时间常数α=0.1,并且假设离散化步长T=1,高斯白噪声Vti的均方差为1 m。根据设定的参数,在Matlab环境下对式(8)和(17)进行仿真,仿真100个采样周期。
GPS绝对定位的误差曲线如图3所示,误差历元差分曲线如图4所示。对图4中的数据特性进行的统计分析如表1所示,可知X轴方向均值为-0.0987,方差为0.8535,Y轴方向均值为-0.1191,方差为1.0169,Z轴方向均值为-0.1445,方差为0.8152。因此,综合图4和表1可知,GPS绝对定位误差历元的差分结果近似于零均值的高斯白噪声。
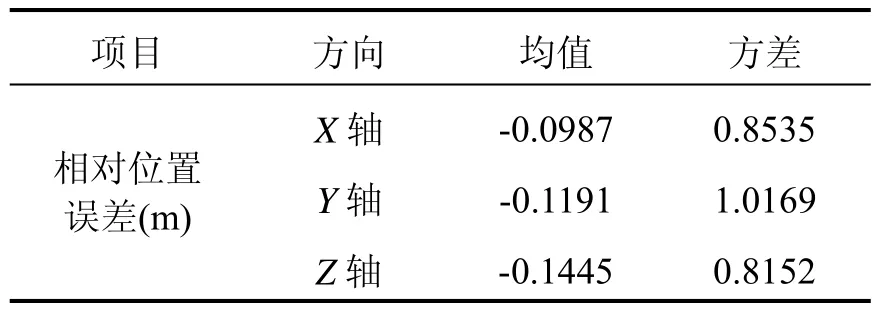
表1 GPS定位误差历元差分特性统计Tab.1 Statistics of differential value of GPS epochs
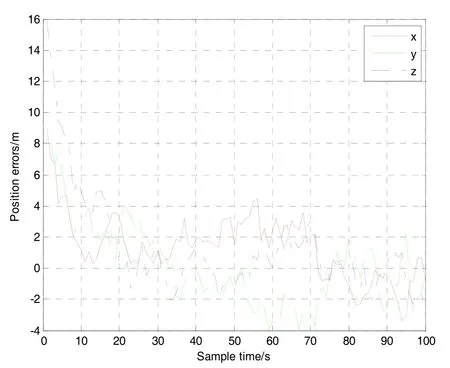
图3 GPS定位误差曲线Fig.3 GPS positioning errors
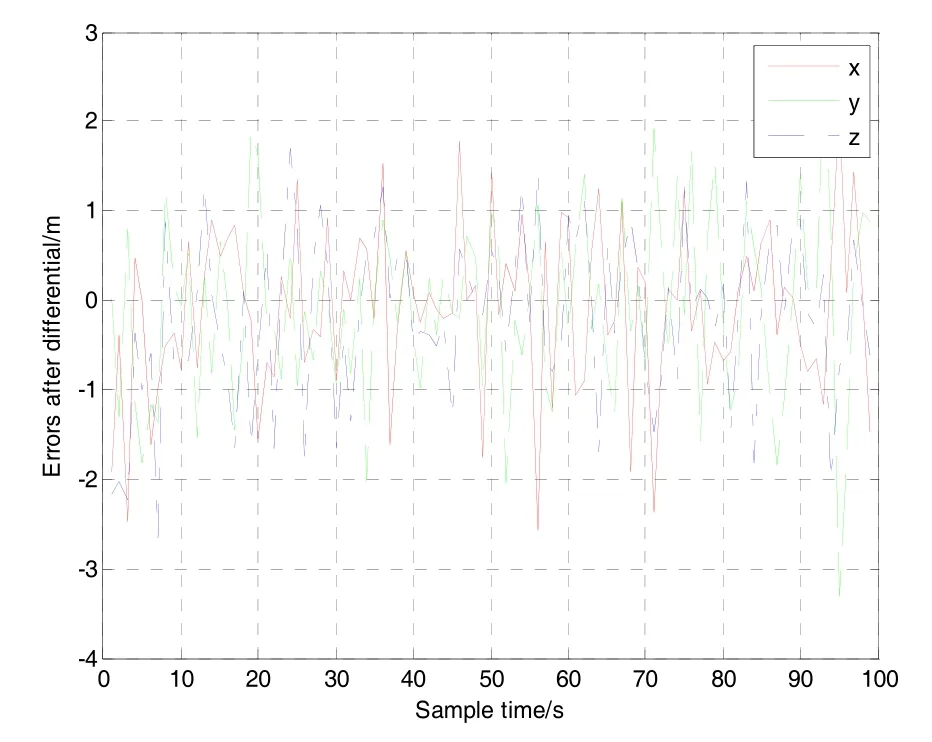
图4 GPS定位误差历元差分曲线Fig.4 Differential errors of GPS positioning errors sequences
如图5所示是基于 GPS的位移量测算。均值为1.5914 m,方差为 0.4342,同时可根据式(17)计算得100个采样周期内由辅助初值和GPS确定的相对距离估计误差的左右边界:

综上可知,重构误差可能是如式(17)所示的区间内的任意值。而其左右边界的外推速度一方面依赖于GPS绝对定位的误差特性,另一方面依赖于服务星的相对运动方向,式(17)等号成立的条件是服务星沿视线方向接近或撤离。
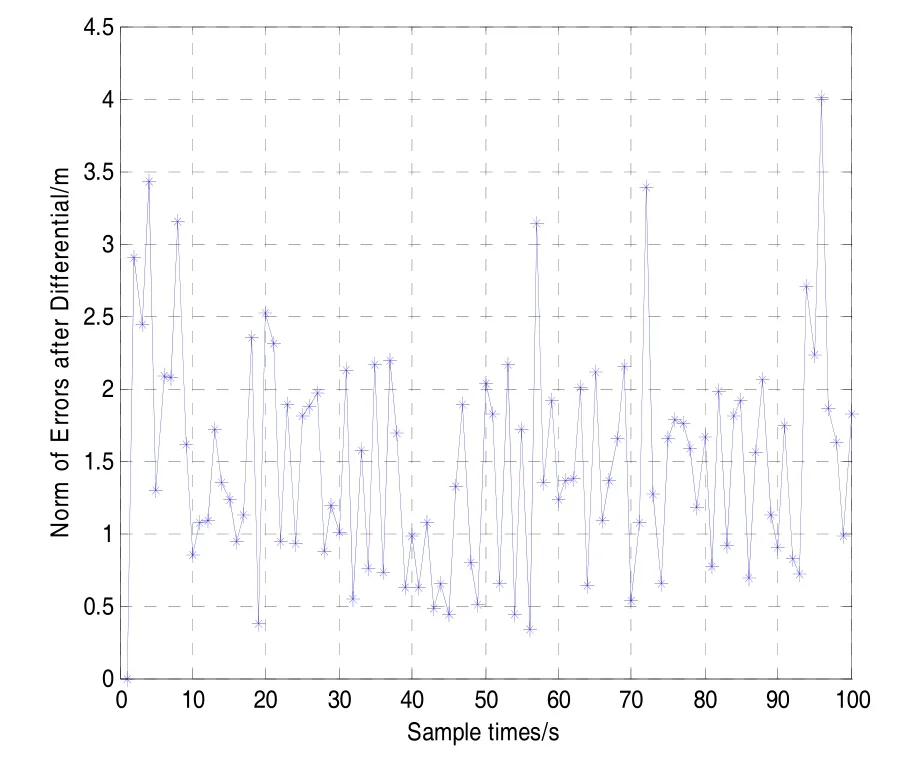
图5 基于GPS的位移测算误差Fig.5 Error of displacement based on GPS
同时,为了对本文的“边-角-边”递推方法与文献[11]中“角-边-角”递推方法进行误差特性的横向比较,并分析其使用性,这里以前述仿真中式(17)右等号成立时的递推误差变化情况(即递推误差最大的情况)与文献[11]的进行垂直于视线方向机动时的误差变化情况(即误差最小的情况)进行比较,其相对距离递推误差计算式为:
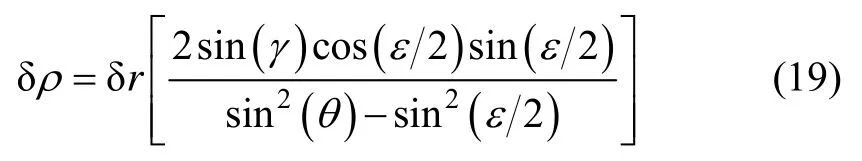
式(19)中各个参量具体定义见文献[11]。
根据目前元器件可得情况,取测角误差为10-3rad,令初始相对距离为30 km,单次机动距离为100 m,机动方向垂直于视线方向,GPS定位误差特性同上,对式(19)进行仿真,仿真时长同样为100 s。可以得到如图6所示的对比结果。
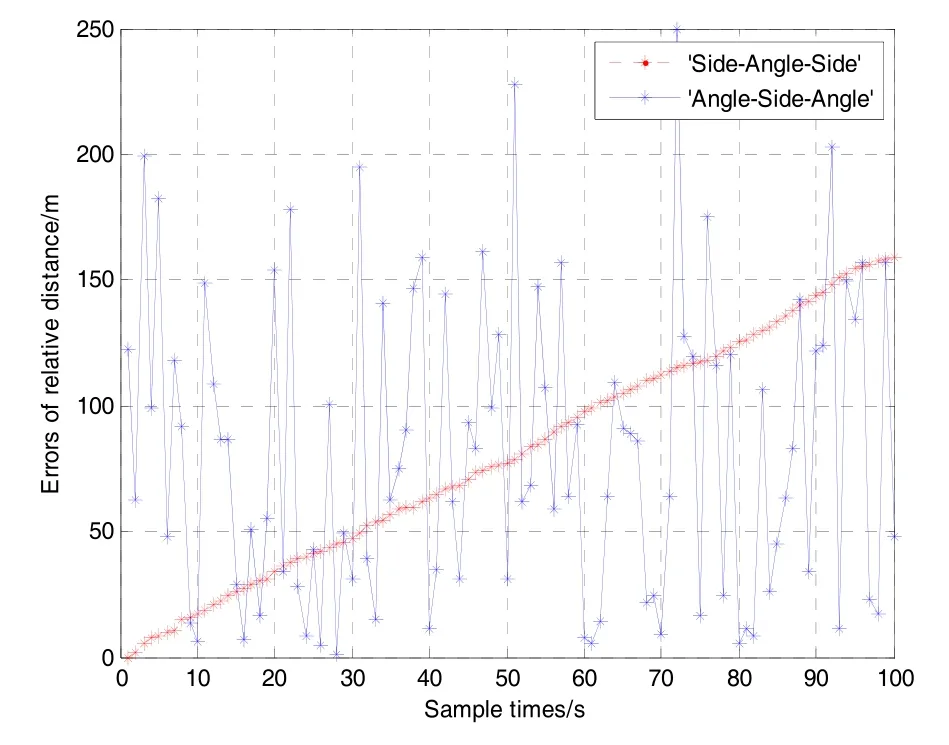
图6 极端误差与最优误差的对比Fig.6 Estimation errors comparing
图6中,“角-边-角”方法相对距离计算的误差均值约为76.11 m,均方差约为56.83 m;本文的“边-角-边”方法相对距离计算的误差均值约为75.21 m,均方差约为42.63 m。从统计的数值上看,在前述仿真条件下,100 s的仿真时间内“边-角-边”算法的极端误差略优于“角-边-角”算法的最优误差。但是,“边-角-边”算法的极端误差呈线性增长状态,随着时间的推移该极端误差必然会大于“角-边-角”的最优误差。然而,值得强调的是,当服务星沿视线方向运动时,尽管“边-角-边”算法的误差累积增长,而“角-边-角”算法则是完全失效的。因此,通过上述比较和分析,本文提出的相对距离递推算法具有其特定的优势。
3.2 重构仿真
首先,令服务星和目标器自由飞行,初始时刻两星的轨道根数如表2所示,此时服务星位于目标器下方约13 km,后方约35 km的位置,相对距离约为37 km。同时,设置CCD输出频率为1 Hz,安装误差和测量噪声均方差为10-3rad;GPS输出频率为1 Hz,定位误差为1 m,测量噪声均方差为0.2 m,其他参数同3.1节。

表2 初始轨道根数Tab.2 Initial orbital elements
然后,为了测试算法的性能和对辅助初值的敏感性,分别两种工况的仿真。
工况一:辅助的相对距离初值误差为10 m。相对距离递推误差结果如图7所示,递推误差总体上呈现波动的缓慢增长趋势,经统计误差均值约为9.21 m,均方差约为3.73 m。
工况二:辅助的相对距离初值误差为100 m。相对距离递推误差结果如图8所示,递推误差的变换趋势同图7,均值约为101.05 m,均方差约为4.05 m。
综合图7和图8可知,递推误差的增长速度与递推初值误差的大小基本没有关系,但是初值误差大小却在整个递推过程中得到传递和保持,这个现象与2.2节中对递推误差的理论分析结果一致,从而也验证了理论分析结果的正确性。
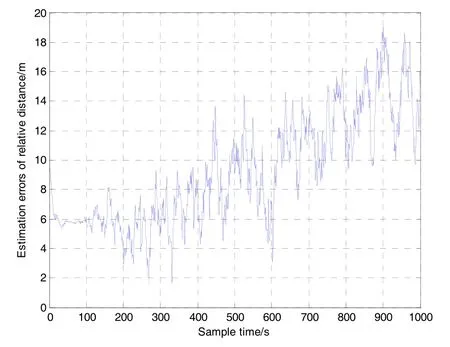
图7 Case 1相对距离递推误差Fig.7 Estimation errors of relative distance in Case 1
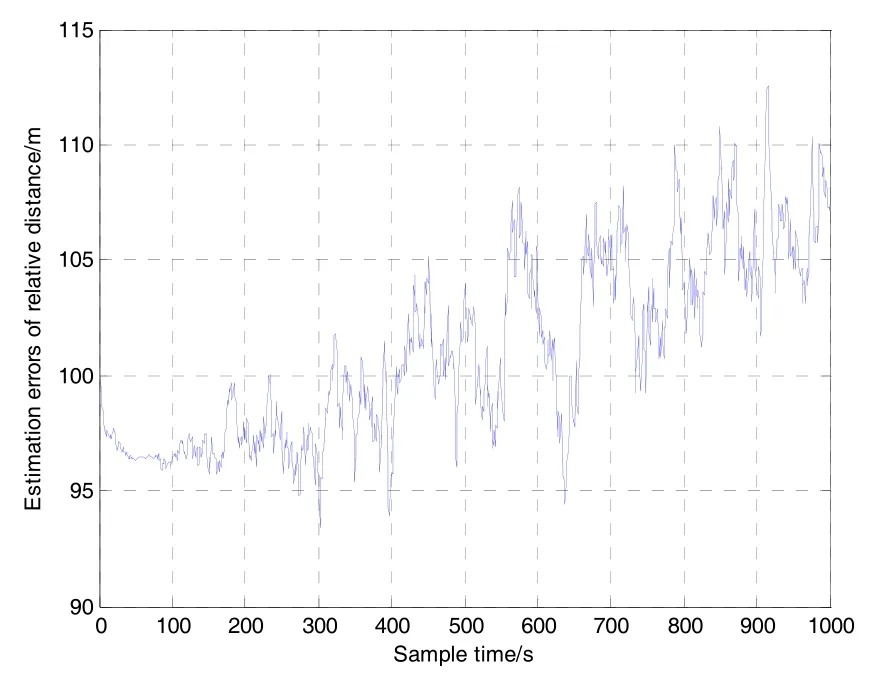
图8 Case 2相对距离递推误差Fig.8 Estimation errors of relative distance in Case 2
4 结 论
本文针对单测角相对导航技术的核心问题——相对距离重构算法展开研究,首次提出了基于初值辅助的 CCD/GPS相对距离重构算法。文章首先分析了传统重构方法的几何原理,指出了其“角-边-角”确定三角形的数学本质,同时分析了传统方法的优缺点,并且在此基础上从“边-角-边”规则的视角提出本文的新算法;然后详细给出了本文重构算法模型的推导过程,并进行了该算法重构误差的理论分析,给出了误差边界模型;最后对重构误差和两种工况的相对距离重构进行了仿真验证和分析。仿真结果表明该重构算法能够较为精确的重构出相对距离,重构精度主要取决于辅助的初值精度。
为了实现相对距离重构算法与单测角导航滤波算法的有机结合,下一步将进一步深入研究所提重构算法的误差特性并建立误差模型。
(References):
[1]梁斌,杜晓东,李成,等.空间机器人非合作航天器在轨服务进展研究[J].机器人,2012,34(2):242-256.Liang B.,Du X.D.,Li C.,et al.Advances in space robot on-orbit servicing for non-cooperative spacecraft[J].Robot,2012,34(2):242-256.
[2]王常虹,曲耀斌,任家栋,等.非合作编队卫星姿轨一体化滤波新方法[J].中国惯性技术学报,2012,20(6):663-669.WANG Chang-hong,QU Yqo-bin,REN Jia-dong,et al.New integrated attitude and orbit filter for non-cooperated satellite formation[J].Journal of Chinese Inertial Technology,2012,20(6):663-669.
[3]Chari R J.Autonomous orbital rendezvous using anglesonly navigation[D].Massachusetts Institute of Technology,June 2001.
[4]Woffinden D C,Geller D K.Relative angles-only navigation and pose estimation for autonomous orbital rendezvous[J].Journal of Guidance control and Dynamics,2007,30(5):1455-1469.
[5]Woffinden D C,Geller D K.Optimal orbital rendezvous maneuvering for angles-only navigation[J].Journal of Guidance control and Dynamics,2009,32(4):1382-1387.
[6]Li J R,Li H Y,Tang G J.Research on the strategy of angles-only relative navigation for autonomous rendezvous[J].Science China Technological Sciences,2011,54(7):1865-1872.
[7]刘光明,廖瑛,文援兰,等.基于双星编队的空间非合作目标联合定轨方法[J].宇航学报,2010,31(9): 2095-2100.LIU Guang-ming,LIAO Ying,WEN Yuan-lan,et al.Twosatellite formation-based non-cooperative space target integrated orbit determination[J].Journal of Astronautics,2010,31(9):2095-2100.
[8]苏建敏,董云峰.非合作机动目标天基测角定轨研究[J].航天控制,2011,29(3):36-42.SU Jian-min,DONG Yun-feng.The orbit determination of non-cooperative maneuvering target by applying spacebased bearing-only measurement[J].Aerospace Control,2011,29(3):36-42.
[9]Chen T,Xu S.Double line-of-sight measuring relative navigation for spacecraft autonomous rendezvous[J].Acta Astronautica,2010,67:122-134.
[10]Wang K,Chen T,Xu S.A method of double line-of-sight measurement relative navigation[J].Acta Aeronautica et Astronautica Sinica,2011,32(6):1084-1091.
[11]Woffinden D C.Angles-only navigation for autonomous orbital rendezvous[D].Utah State University,May 2008.
[12]Crassidis J L,Alonso R,Junkins J L.Optimal attitude and position determination from line-of-sight measurements[J].Journal of the Astronautical Sciences,2000,48(2-3):391-408.
[13]Kim S,Crassidis J L,Cheng Y,Fosbury A M.Kalman filtering for relative spacecraft attitude and position estimation[J].Journal of Guidance,Control,and Dynamics,2007,30(1):133-143.
[14]范利涛,郑伟,汤国建,等.基于平方根UKF滤波的轨道机动飞行器自主导航方法[J].中国惯性技术学报,2008,16(6):687-693.FAN Li-tao,ZHENG Wei,TANG Guo-jian J,et al.Autonomous navigation method for orbital maneuver vehicle based on square-root unscented Kalman filter[J].Journal of Chinese Inertial Technology,2008,16(6):687-693.
Novel reconstructing algorithm of relative distances for angle-only relative navigation
GONG Bai-chun1,2,LUO Jian-jun1,2,MA Yue3
(1.College of Astronautics,Northwestern Polytechnical University,Xi’an 710072,China;2.Science and Technology on Aerospace Flight Dynamics Laboratory,Xi’an 710072,China;3.96271 unit of PLA,Luoyang 471600,China)
Aiming at the key issue of the relative distance re-constructing in the angle-only relative navigation for mid and far-range rendezvous with space non-cooperative target,a novel algorithm is presented based on GPS absolute positioning,CCD relative angles of LOS measuring and an aided initial value of the relative distance.The mathematical substance and the characteristic of the traditional method are analyzed.And a re-constructing model is established based on the triangle principle integrated with the differential value between the sequences of GPS positioning at two different epochs.After that,the error of the reconstructing is analyzed by means of mathematical derivation and simulation.At last,two cases simulation of relative distance re-constructing is conducted,and the results show that the proposed algorithm can estimate the relative distance,and the estimation precision depends on the performance of the initial relative distance aided exterior.Thus,the proposed algorithm has important research and application value.
space non-cooperative target;relative navigation;angles-only;relative distance;
V448.22+4
A
1005-6734(2014)03-0340-06
10.13695/j.cnki.12-1222/o3.2014.03.012
2014-01-08;
2014-04-21
国家自然科学基金项目(61004124);西北工业大学博士论文创新基金项目(CX201404)
龚柏春(1987—),男,博士研究生,从事飞行动力学与控制、组合导航研究。E-mail:gbc1987@163.com
联 系 人:罗建军(1965—),男,教授,博士导师。E-mail:jjluo@nwpu.edu.cn

