舰船波浪中航行时的变形分析及其IMU实时测量方法
戴洪德,柳爱利,卢建华,戴邵武,孙玉玉
(1.海军航空工程学院 控制工程系,烟台 264001;2.海军航空工程学院 干部处,烟台264001)
舰船波浪中航行时的变形分析及其IMU实时测量方法
戴洪德1,柳爱利1,卢建华1,戴邵武1,孙玉玉2
(1.海军航空工程学院 控制工程系,烟台 264001;2.海军航空工程学院 干部处,烟台264001)
大型舰船在水面上航行过程由于波浪的作用会产生一定的变形,该变形会降低舰船上姿态信息的精度,影响舰载武器系统的作战效能,针对这一问题,首先对舰船的变形进行理论分析,计算舰船所承受的波浪载荷,将波浪载荷加载到舰船的有限元模型,经计算得到的甲板各节点的角位移及线位移信息,以此来分析舰船的变形。在舰船的关键战位点安装由陀螺仪和加速度计组成的惯性测量单元(IMU),将IMU的输出信息与舰船主惯导的输出信息进行匹配,设计舰船变形估计的卡尔曼滤波器,实时估计IMU安装处的甲板变形角,为舰载武器装备提供准确的局部姿态信息,实验结果证明了所提方法的有效性。
变形;波浪载荷;有限元;惯性测量单元;卡尔曼滤波
随着现代战争对武器系统精确打击能力的要求不断提高,大型舰船上装备的飞机、导弹甚至炮弹等多种武器系统都装备了惯性导航系统或惯性/卫星组合导航系统,惯导系统在进入正常工作前首先必须进行初始对准[1-2],也就是确定惯性导航系统的初始位置、速度及姿态等信息,在舰船这样的动基座上完成初始对准一般都采用传递对准的方式,当舰船较大时,由于舰船不是一个绝对刚体,舰船海上航行时会因船体变形出现失调角误差。引起这些变形误差的因素包括日晒、老化、武器发射冲击、转舵操作、载荷变化等[3],甲板纵向平面绕纵摇轴方向的变形甚至可能达几十个角分,这样传递对准的准确性会大大降低[2],所以需要对舰船的变形进行分析并测量估计,从理论上讲,舰船的挠曲变形角可以通过卡尔曼滤波进行估计[4-5],但在实际应用中很难建立足够精确的模型,以消除船体变形的影响[2]。依据物理机制建立的模型受实际因素的影响,通常不具有实际应用价值[6-7]。近年来各国的海军、导航界和造船界纷纷致力于船体变形的分析、测量与校正技术的研究,以减小因船体变形引起的误差[3,8-11],为舰载武器装备提供准确的局部姿态信息。
针对这一问题,本文首先介绍了一种基于有限元分析和切片理论相结合的舰船甲板变形计算方法,对舰船进行切片划分,计算船体外表面切面所受的脉动压力,根据与舰船切片相对应的有限元模型节点的单位内法矢,投影得到作用于有限元节点上的波浪载荷,通过有限元计算方法计算出各节点的应力响应和变形响应;其次在舰船上关键战位点安装惯性测量单元(IMU:Inertial Measurement Unit),将其输出与舰船主惯导的输出进行匹配,设计卡尔曼滤波器估计舰面上IMU安装处实时、精确的挠曲变形,并与有限元分析的数据进行对比,验证了本文研究思路的正确性和所提方法的有效性。
2 基于有限元的舰船变形分析
2.1 舰船结构有限元模型
与基于简单梁理论的简化公式相比,结构有限元分析能更加准确地反映具体舰船结构的特性和细节,而且能与波浪外载荷相匹配,从而确切地反映和模拟真实船体的结构。要精确分析计算舰船在多种载荷作用下的整体弹性变形,首先就是要建立舰船的全船有限元分析模型[12-13]。选取舰船结构中典型的甲板板架,采用三层甲板+底板结构。纵桁和横梁都是 T型材,纵桁两端是舱壁,横梁两侧是舷侧,带板因素计入横梁和纵桁的惯性矩中。全船共设计有甲板船板的厚度,纵桁的腹板高度、厚度和面板宽度,横梁的腹板高度、厚度和面板宽度共七个变量,结构应满足局部强度和最大刚度条件的约束。所建舰船结构的有限元模型主要使用 SHELL63板壳单元、BEAM188梁单元和MASS21点单元。SHELL63单元是具有弯曲刚度的板壳单元,能够较好模拟舰船局部结构的各种板壳元件。BEAM188单元能定义梁元的截面形状,如工字梁、球扁钢等,且适用于分析细长的梁。点单元MASS21用来对舰船进行质量补偿。
采用四点自由支持约束法来设定模型的边界条件,在经典结构力学中,当舰船静止在水面上,一般将结构模型的约束选为自由支持。自由支持的模型是一端限制平动,放开转动,另一端限制两个方向自由度平动,不限制转动。基于这个原理模型,将四点取在水线上,船体三点船艏一点,即在舰船水线中心处限制模型的三个平动自由度,限制船体模型外板在水线处的两个交点的两个方向平动自由度,而在船舷和水线相交的一点,仅限制沿和水线垂直方向上一个自由度,并且不限制转动自由度。图1建立了一个具有3层甲板的大型舰船的有限元模型。
图1 船体部分网格划分图及3D效果图Fig.1 Grid sketch of ship body and sketch of 3D model
2.2 海浪的数学描述及仿真模型
根据海浪随机理论以及海浪谱的波能谱密度理论,采用多个(n个)随机正、余弦波叠加来模拟海浪,数学模型如式(1)所示[14]:
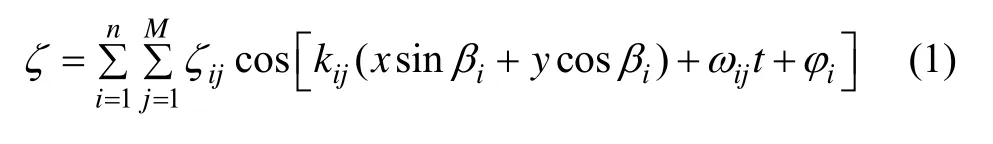
式中:ζij、kij、iβ、ijω、iφ分别为单元规则波的波幅、波数、传播方向、角频率和相位;n为单元规则波的个数;M为波能谱的能量分布图上频率ω的划分个数。
如果采用ITTC的双参数谱(又称ISSC波谱[2])定义波能谱密度函数,在波浪周期T1和有义波高hs有统计资料供使用的情况下,波幅ζ定义为:
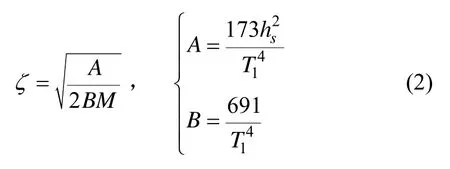
由线性波动理论,波数k与圆频率ω满足色散关系(Dispersion Relation),即

式中:g为重力加速度,h为水深。当水深h大于波长的一半时,k=ω2/g。浪向角β显示了单元规则波的传播方向,频率的分割程度是决定海浪复现精度的一个因素,随机相位可以采用混合同余法,在0~2π内随机选取。
2.3 波浪中舰船载荷分析
根据海情和波浪谱资料在海浪仿真模型确定了中等海情下单一规则波的波幅ζ=3 m、波数k=0.252g-1、浪向角β=30°、ω=0.25 Hz、随机相位iε后,并采用在此种海情下舰船六自由度运动的经验数据(表1),舰船航速设定为16 kn[14-15]。

表1 不同海况下舰船运动参数Tab.1 Motion parameters in different sea situations
应用切片理论通过求解船舶在规则波中的运动方程式得到舰船各横剖面所受的脉动压力[16]P(表2)。将舰船有限元模型上与水面接触的节点的坐标向水面随船平移坐标系上作投影,得到这些节点上的单位内法向矢量n⇀之后,可以得到作用于船体单位剖面内的波浪载荷。
2.4 计算各节点运动数据
将2.3节分析得到的波浪载荷加到2.1节建立的有限元模型,加载方式如图2所示。在仿真实验中,以5 m为间隔,这样沿水线X轴方向就确定了240×2=480个横剖面,船体瞬时湿表面网格采用文献[10]所提出的方法生成,即考虑瞬时物面变化引起的各种非线性因素,在时域内建立起船体非线性运动方程。在每一时刻,认为船体以其瞬时平均湿表面为平均位置做简谐运动。计算出甲板各节点的位置、速度、加速度、姿态、角速度等运动数据。
3 基于IMUs的变形实时估计模型
对于大型舰船,在甲板各战位点处设置惯性测量单元IMU(陀螺+加速度计),通过网络和综合信息处理计算机构建一个惯导网络,各个IMU通过同步取数将测量信息送往综合信息处理计算机,综合信息处理计算机将各个 IMU提供的信息进行融合后再向所有战位点发送姿态信息。当某个局部基准发生故障时,综合信息处理计算机可进行系统重构,继续向各战位点发送姿态信息。通过这种方式可以为舰船上关键战位点提供更丰富、准确的载舰状态信息。
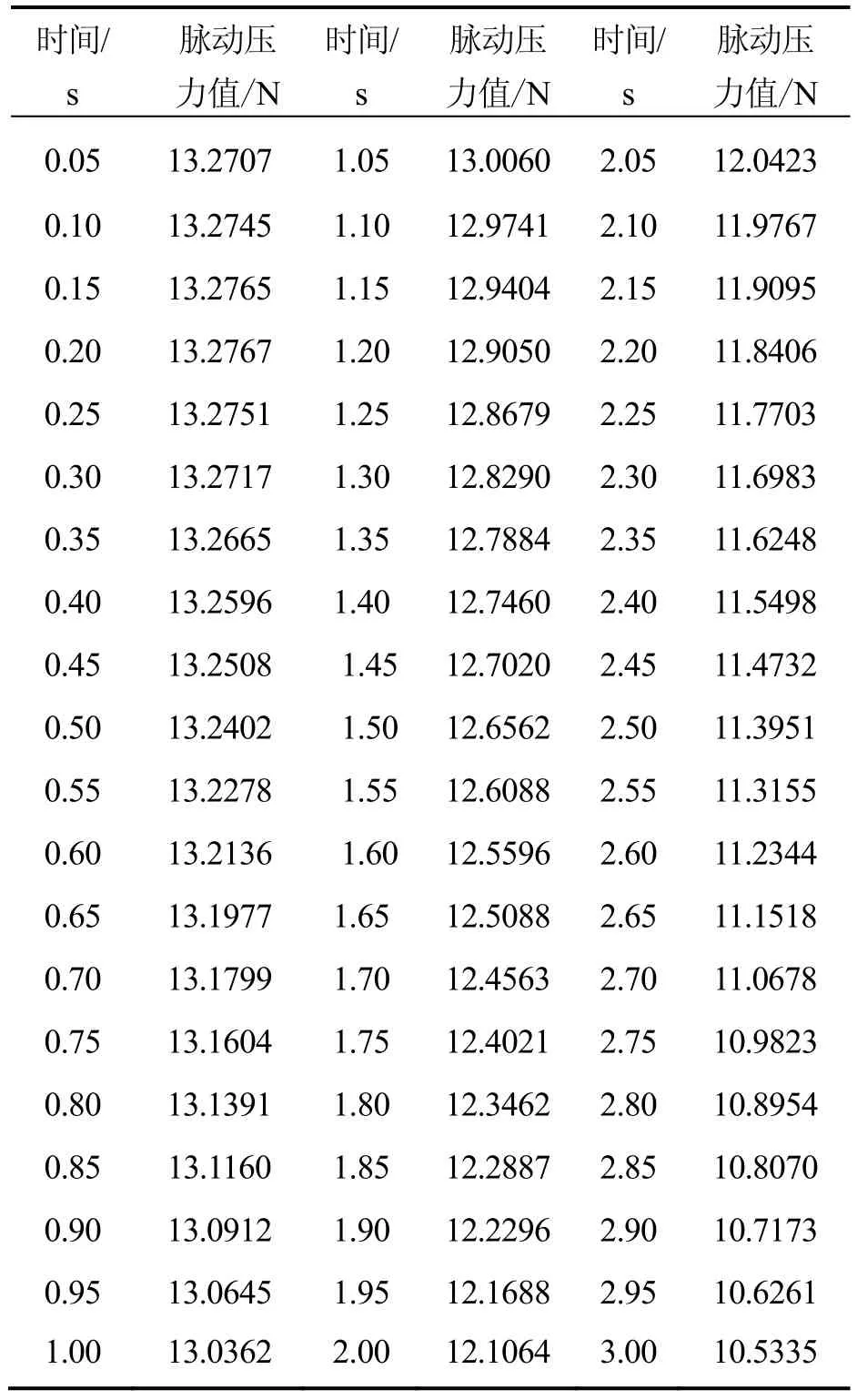
表2 x=0横剖面的脉动压力数据Tab.2 Pulsation pressure data of cross section x=0
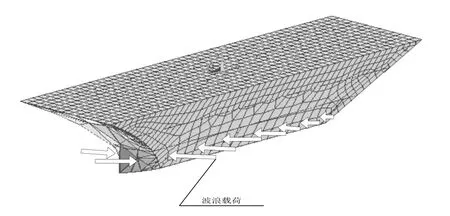
图2 舰船上的波浪载荷加载方式Fig.2 Wave load of ship
20世纪80年代以来,国内外相继发表了一些文献,利用惯性测量匹配法来检测变形失调角并消除误差。俄罗斯圣彼得堡电工大学提出了采用两套三轴激光陀螺组件测量舰船变形的方案[3],利用两惯性测量组件输出的角速度,采用卡尔曼滤波来估算出舰船的变形角。国内汪顺亭等推导了三种惯性测量匹配法测量船体变形的实施方案[9]。
本课题组研究了在舰船上安装惯性测量单元IMU,通过IMU输出的速度增量以及角速度与舰船主惯导信息相匹配的方法,实时估计出 IMU安装处实时、精确的变形角。在舰船中心位置的主惯性导航系统MINS(Main Inertial Navigation System)的坐标系定义为x轴指向舰船的右侧舷,y轴指向舰艏,z轴垂直于舰船向上,与x和y轴构成右手直角坐标系。甲板上IMU的坐标系,沿着甲板的方向与MINS的坐标系定义类似,他们的关系如图3所示。
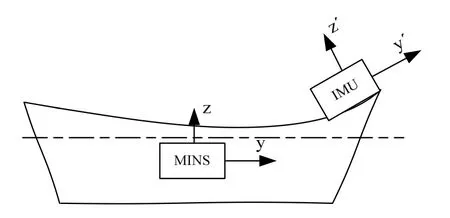
图3 舰船主惯导与IMU相对位置及坐标系示意图Fig.3 Relative position and frame between the main INS of ship and IMU
其他用到的坐标系作如下定义:n:导航坐标系(舰船所在位置的当地地理坐标系);m:主惯性导航系统MINS坐标系(oxyz坐标系);sr:真实的IMU坐标系(ox′y′z′);sc:计算的 IMU 坐标系;:从MINS坐标系到计算的 IMU坐标系的坐标变换方向余弦矩阵;:从MINS坐标系到真实IMU坐标系的坐标变换方向余弦矩阵;:主惯导的姿态矩阵。
定义变形角为主惯导MINS坐标系m到真实IMU坐标系sr之间随时间变化的误差角度,用ψa表示(假设为小角度);同时用ψm(t)表示m坐标系和 sc坐标系之间随时间变化的误差角度。它们之间的关系如图4所示。
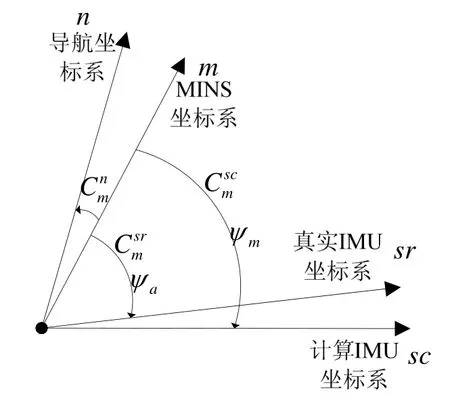
图4 坐标系之间关系Fig.4 Relationship among the defined frames
3.1 系统方程
美国学者Kain J.E和Cloputier J.R等在上世纪末提出了基于载体坐标系内定义的姿态误差的全新误差模型,介绍了基于该误差模型的“速度+姿态角”匹配的快速对准方法[7],很快就引起了国内外研究者的广泛关注和深入研究[6,17-18],并于1998年在美国F-16战机上进行了试飞验证,在 10 s内达到了1 mrad(3.4377′)的对准精度[6]。作者将该思想应用到舰船变形估计中,根据实际需要重新选择了观测变量,推导了估计变形角的 Kalman滤波器量测模型,快速准确地估计出舰船的变形角。
参考kain在文献[7]的误差模型,以及作者前期的研究[19-21]选取速度误差、计算姿态误差、真实姿态误差为滤波器设计时的状态方程,定义状态向量为:

误差方程为:
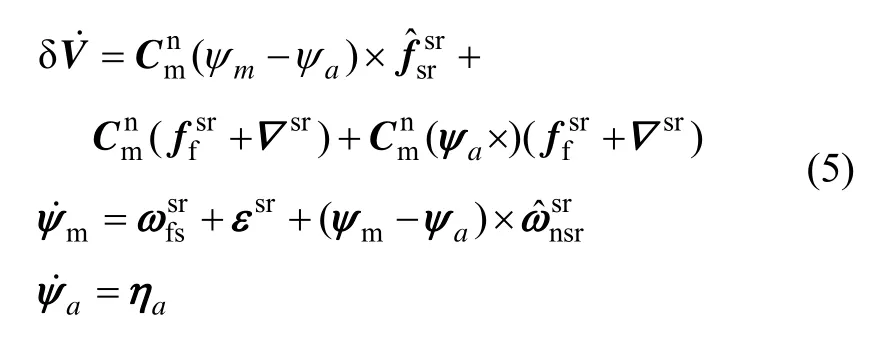
式中,aη为白噪声过程。根据式(5)可以写出状态方程:

3.2 观测方程
速度误差在文献[7]中定义为 IMU处的的速度与经过杆臂误差补偿的主惯导速度之差:
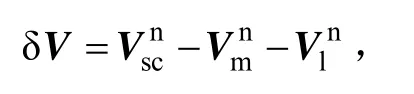
则k时刻的速度误差可以表示为:
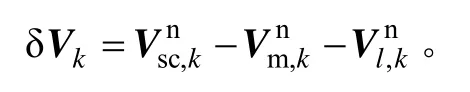
因为加速度计输出的是速度增量的形式,所以k时刻IMU、主惯导的速度及杆臂速度都可以表示为k-1时刻的速度加k-1时刻到k时刻的速度增量的和,所以:
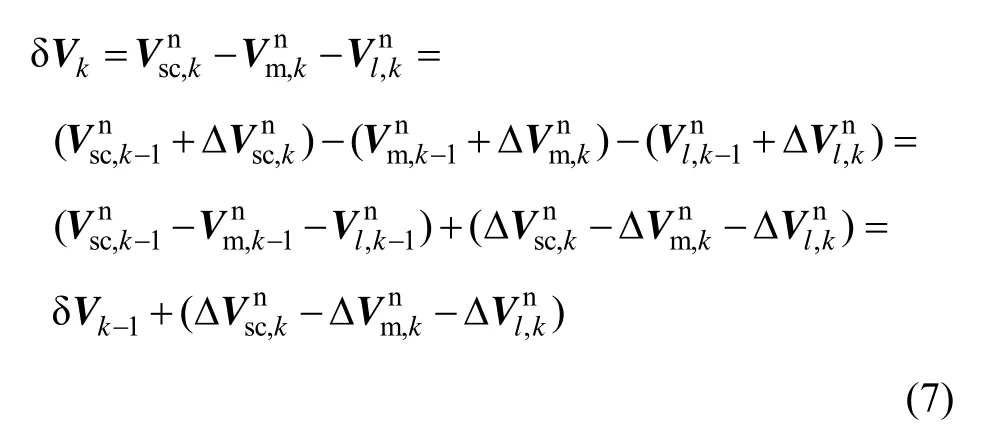

所以:
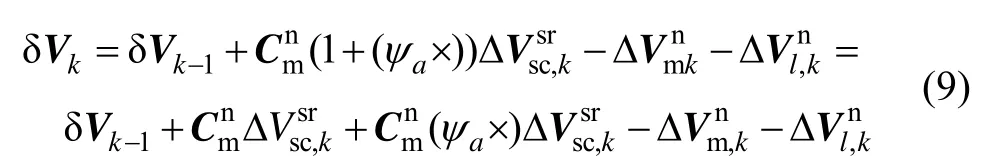
将已知量和状态量分开整理得:
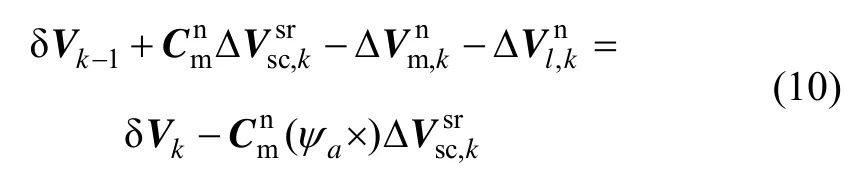
定义速度增量量测为:
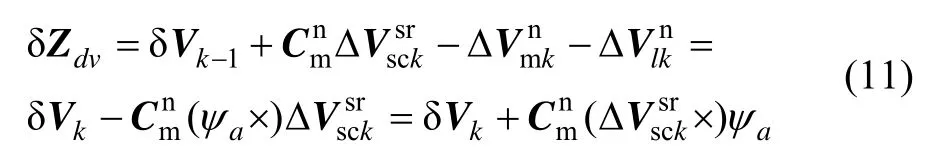
可以用状态向量表示如下:
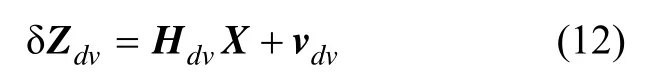
主惯导的角速度测量值为:

IMU的角速度测量值为:

量测差值定义为:
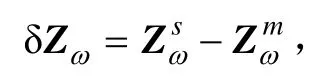
所以量测模型为:
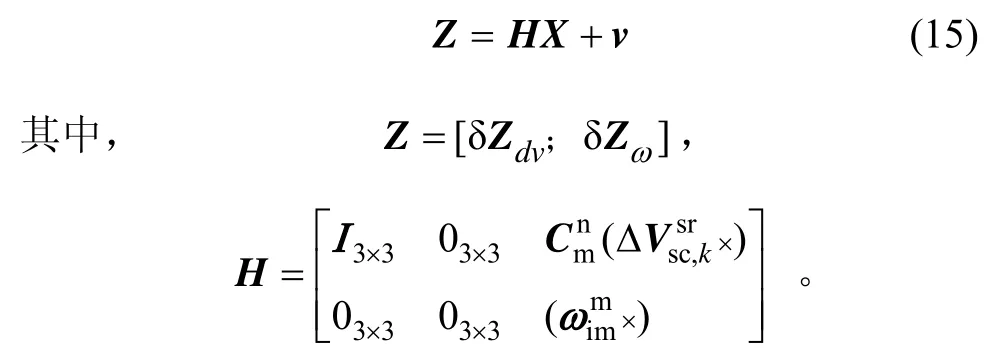
4 计算机仿真分析
应用第2节的舰船结构分析理论模型,得到舰船在波浪作用下的变形数据,再根据舰船上安装的IMU测量舰船各个部分的角运动和线运动值,利用卡尔曼滤波算法估计出舰船各战位点的变形角,变形角估计框图如图5所示。
在仿真中,舰船主惯导陀螺仪常值漂移为 0.02(°)/h,随机漂移为0.01 (°)/h,舰船主惯导导航解算周期15 ms,变形估计滤波周期75 ms,仿真总时间10 s,IMU陀螺仪常值漂移为2 (°)/h,随机漂移为1 (°)/h,刻度系数误差2×10-4,加速度计常值偏置200 μg,随机偏置50 μg,刻度系数误差2×10-4,载体所在纬度为34°,经度为108°,杆臂长度为[100;30;5]m,根据2.4节得到的IMU安装处的速度增量、角速度数据得到IMU的测量数据,按照第3节中推导的惯性匹配方法估计出IMU安装处的甲板变形角。取2.4节计算出的 IMU安装处对应的节点的姿态数据为变形的真实值,与kalman滤波得到的变形角估计值比较,得到舰船甲板动态变形惯性测量方法的误差,如图6所示。
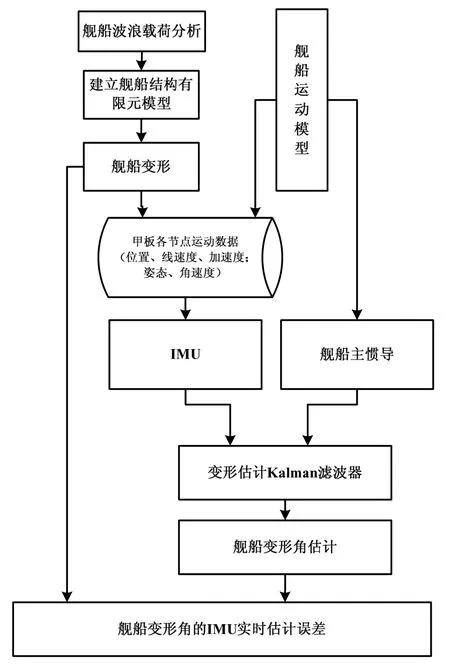
图5 变形角估计框图Fig.5 Estimation diagram of deformation angle
图6为舰船甲板9117号节点处估计得到的变形角与实际变形角的误差图,从仿真结果可以看出,本文所提出的基于 IMU输出匹配的舰船甲板动态变形估计方案,对舰船变形角的跟踪能够在10 s内收敛,估计误差的具体值为[0.367;-0.740;0.723]角分。
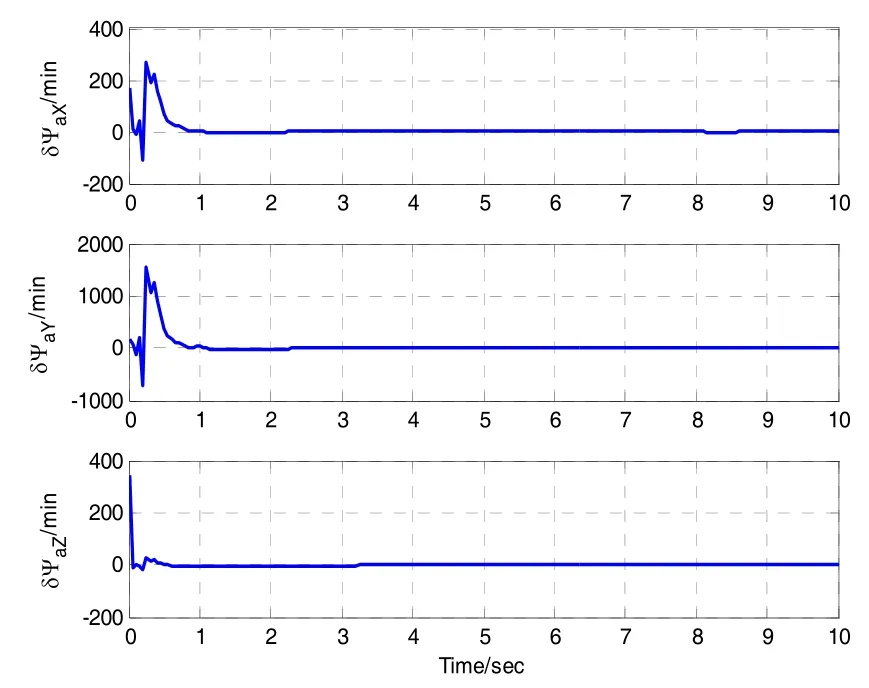
图6 变形角估计误差Fig.6 Estimation error of deformation angle
5 结 论
本文首先建立了舰船结构的有限元模型及海浪的数学模型,分析海浪作用下舰船的受力情况,计算出舰船各个节点的变形运动,分别运用IMU的陀螺仪和加速度计测量出安装位置的角运动和线运动,与舰船主惯导的输出信息匹配,应用卡尔曼滤波器准确估计出舰船关键战位点的姿态信息。仿真结果证明了该方法的有效性。由于舰船上位置有限,且IMU成本较高,所以下一步将研究如何根据舰船上安装的有限IMU得到的变形数据,估计出舰船上任意位置的变形信息。
(References):
[1]Noureldin A,Karamat T B, Georgy J. Fundamentals of inertial navigation,satellite-based positioning and their integration[M]. Berlin:Springer-Verlag Berlin and Heidelberg GmbH &Co.K,2013.
[2]Titterton D H,Weston J L.Strapdown inertial navigation technology[M].2ed.The Institution of Electrical Engineers,2004.
[3]Mochalov A C,Kazantsev A V.Use of the ring laser units for measurement of the moving object deformation[C]//Proceedings of SPIE.2002,4680:85-92.
[4]Crisan D,Rozovskii B L.The Oxford handbook of nonlinear filtering[M].Oxford:Oxford University Press,2011.
[5]Zarchan P,Musoff H.Fundamentals of Kalman filtering:a practical approach [M].Third ed.Virginia:American Institute of Aeronautics and Astronautics,2009.
[6]Shorttelle K J,Graham W R,Rabourn L C.F-16 flight tests of a rapid transfer alignment procedure[C]//Proceedings of the IEEE Position Location and Navigation Symposium,1998:379-386.
[7]Kain J E,Cloutier J R.Rapid transfer alignment for tactical weapon applications[C]//Proceedings of the AIAA Guidance,Navigation and Control Conference,1989.
[8]万德钧,刘玉锋.消减舰船变形的影响和为全舰提供高精度姿态基准[J].中国惯性技术学报,2005,13(4):77-82.WAN De-jun,LIU Yu-feng.Summary on removing influence of ship deformation and providing accurate attitude references for warship[J].Journal of Chinese Inertial Technology,2005,13(4):77-82.
[9]汪顺亭,汪湛清,朱昀炤,等.船体变形的监测方法及其对航向姿态信息的修正[J].中国惯性技术学报,2007,15(6):635-641.WANG Shun-ting,WANG Zhan-qing,ZHU Yun-zhao,et al.Monitoring on ship hul deformation and correction for heading and attitude information [J].Journal of Chinese Inertial Technology,2007,15(6):635-641.
[10]魏学通,马利民,庄伟东,等.一种舰船变形测量方法的研究与应用 [J].中国惯性技术学报,2006,14(3):74-77.WEI Xue-tong,MA Li-min,ZHUANG Wei-dong,et al.Research on distortion surveying of vessels [J].Journal of Chinese Inertial Technology,2006,14(3):74-77.
[11]周瑞.基于有限元的舰船推进轴系合理校中计算方法[J].中国舰船研究,2012,7(3): 74-78.ZHOU Rui.Calculation method for ship propulsion shafting alignment based on finite element analysis[J].Chinese Journal of Ship Research,2012,7(3):74-78.
[12]何凯,唐文勇,罗凯,等.复合材料舰船全船有限元分析的建模方法研究[J].中国舰船研究,2011,6(5):83-88.HE Kai,TANG Wen-yong,LUO Kai,et al.Finite element modeling method for composite ship hull[J].Chinese Journal of Ship Research,2011,6(5):83-88.
[13]Crisfield M A,Remmers J J,Verhoosel C V.Nonlinear finite element analysis of solids and structures [M].John Wiley &Sons,2012.
[14]Karnopp D C,Margolis D L,Rosenberg R C.System dynamics:Modeling,simulation,and control of mechatronic systems[M].John Wiley &Sons,2012.
[15]Cuomo G,Allsop W,Bruce T,et al.Breaking wave loads at vertical seawalls and breakwaters[J].Coastal Engineering,2010,57(4):424-439.
[16]Tarrant D,Roberts C,Jones D.Rapid and robust transfer alignment[C]//IEEE Proceedings of Aerospace Control System,1992.
[17]HAO Y,XIONG Z,WANG W,et al.Rapid transfer alignment based on unscented Kalman filter[C]//Proceedings of the 2006 American Control Conference.Minneapolis,Minnesota,USA,2006.
[18]戴洪德,周绍磊,陈明,李娟.基于四元数非线性误差模型的快速传递对准[J].宇航学报,2010,31(10):2328-2334.DAI Hong-de,ZHOU Shao-lei,CHEN Ming,LI Juan.Quaternion based nonlinear error model for rapid transfer alignment[J].Journal of Astronautics,2010,31(10):2328-2334.
[19]柳爱利,戴洪德.基于惯性传感器输出匹配的舰船变形估计方法[J].传感技术学报,2011,24(1):145-148.LIU Ai-li,DAI Hong-de.Deformation estimation of warship based on the match of inertial sensors’ output[J].Chinese Journal of Sensors and Actuators,2011,24(1):145-148.
Deformation analysis and IMU-based real-time measuring method for big ship sailing in wave
DAI Hong-de1,LIU Ai-li1,LU Jian-hua1,DAI Shao-wu1,SUN Yu-yu2
(1.Naval Aeronautical and Astronautical University,Department of Control Engineering,Yantai,264001,China;2.Naval Aeronautical and Astronautical University,Department of Political,Yantai,264001,China)
A large ship always occurs deformation when sailing in water because of the wave load,which will degrade the accuracy of attitude information on the ship and affect the efficiency of the shipboard weapons.Aiming at this problem,the ship’s deformation is analyzed theoretically,and the ship’s wave load is computed,then by loading the computed wave onto the finite element model,the angular displacement and linear displacement can be achieved by calculation.The IMU(Inertial Measurement Unit),which is composed by gyros and accelerators,are installed in the key battle point of the ship,and the output of the IMU are matched with the main inertial navigation system of ship to estimate the deformations in real-time.Besides,a Kalman filter is designed for real-time estimating the deformation angle of the ship deck where the IMU is installed,and providing accurate locale attitude for shipboard weapons.The experiment results verify the availability of the presented method.
deformation;wave load;finite element;inertial measurement unit;Kalman filter
U666.1
A
1005-6734(2014)03-0327-06
10.13695/j.cnki.12-1222/o3.2014.03.010
2013-12-03;
2014-04-08
国家自然科学基金(61203168);博士后(2013m532173);航空基金(20135184007)
戴洪德(1981—),男,博士后,讲师,从事惯性测量及卡尔曼滤波技术研究。E-mail:dihod@126.com

