一种基于多尺度分析的线条重构方法

樊顺利，罗晓晖

西华大学数学与计算机学院，成都 610039

一种基于多尺度分析的线条重构方法

樊顺利，罗晓晖

西华大学数学与计算机学院，成都 610039

1 引言

计算机视觉中，线条检测又被称为曲线结构检测[1]，曲线结构是指具有某一尺度的直线或曲线[2]。到目前为止，针对不同场景设计出来的线条检测算法被应用在了很多不同的领域，例如，解剖学中分割血管、地球科学中提取遥感图像中的河流、道路等，图像中线条特征的识别对后续的图像理解有很大的意义。

文献[1]提出了一个基于高斯以及高斯一阶和二阶导数的滤波器的方法，利用定位中心点和边缘信息检测出线条信息，类似的利用这种几何法找峰值的还有文献[2-3]中提到的算法。另一类线条检测算法是基于边缘检测的，例如文献[4]中提出的基于边缘增强的线条检测。以上基于几何特性和边缘的线条检测算法对线条尺度信息的确定依赖准确的边缘定位。另外还有一类是基于区域分析的线条检测算法，这一类算法最典型的就是利用Hessian矩阵，文献[5]中提到了一种基于Hessian矩阵分析的非参数提取血管的方法，这种方法可以对三维血管进行有效的分割，文献[6]提出的基于区域统计的LWF算法还考虑了算法实时性，另外，文献[7]提出的PCT算法也是基于区域分析的线条分割算法。

现有线条提取算法多用于线条分割，大多利用边缘获取线条的尺度信息，而边缘检测本身就是一个难度较大的问题，较少利用线条的尺度与角度信息对线条进行重构。本文研究了一种基于多尺度空间的线条检测器，自适应地获取线条的尺度和角度信息，结合非极大值抑制[8]，重构图像中具有较大对比度的不同尺度、不同角度的线条。

2 线条重构原理

线条重构，即原始线条的重新构造，根据线条的尺度和角度信息对线条信息进行恢复。重构第一步是信号检测，然后根据检测到信号的一些特性对信号进行重新构造。

2.1 一维曲线模型

理想的一维线条模型是条状形式[1]，一个尺度为2w，高度为h的线条模型描述如下：

理想信号模型示意图如图1所示。

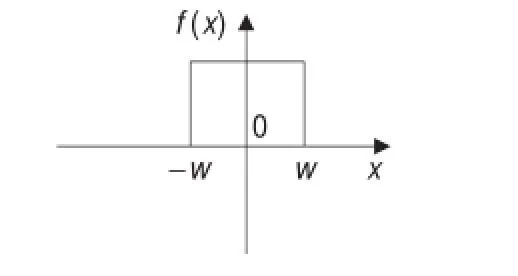
图1 一维信号示意图

2.2 一维线条重构

Lindeberg在文献[9]中规范地定义了多尺度空间。所谓的尺度空间技术就是指从原始图像导出一系列越来越平滑、越来越简化的图像。图像多尺度的基本要求是大尺度下的图像结构为小尺度图像结构的简化，Lindeberg和Koenderink已经证明[10]，唯一可能的尺度核是高斯核。

本文假设信号f(x)为上述公式（1）所描述的情况，即为f2w，h(x)。对信号检测的第一步是利用高斯-拉普拉斯滤波器对信号进行卷积。

能量图的像素值是信号在所有尺度下卷积结果中的全局最大值：

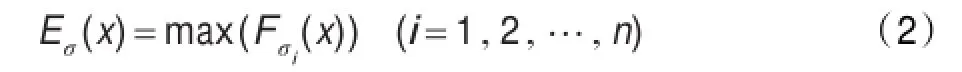
其中n代表尺度空间的个数。Fσi(x)表示在第i个尺度下的卷积结果补偿σ2i：

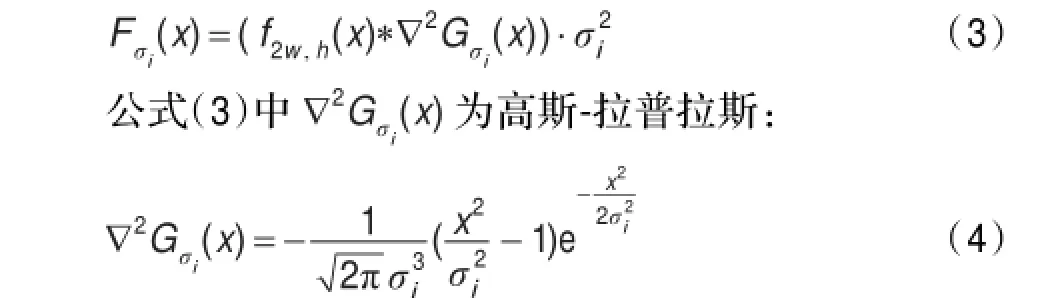
为了保持Lindeberg提出的多尺度空间的稳定性[11]，需要对卷积结果补偿σ2[12]，通过详细的实验对比，Mikolajczyk[13]发现由σ2▽2Gσ的极大值或极小值产生的图像特征比梯度、Hessian以及Harris角点检测等一系列图像函数产生的图像特征更加稳定。

尺度图的像素值是在所有尺度下卷积结果取得全局最大值时对应的尺度。由于信号尺度的有限性，当卷积模板和信号匹配时，在信号的中心位置形成局部极大值。同时可以得到信号的尺度为2σ，证明如下：图2表明了多尺度滤波器对理想信号进行检测重构的实验过程。

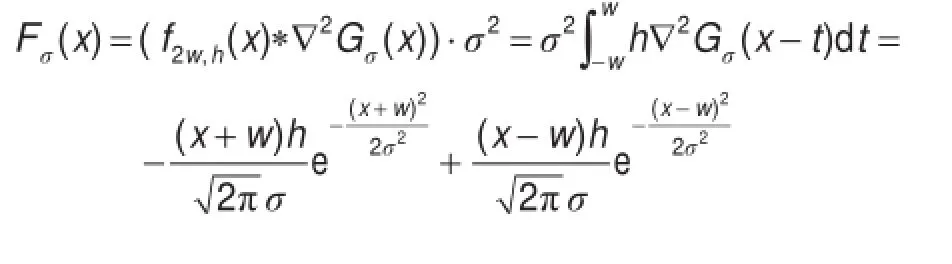
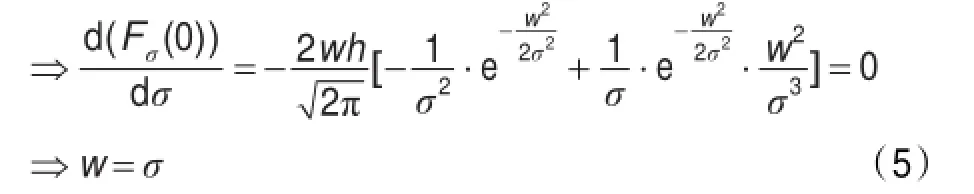
在信号中心点取得局部极值，于是

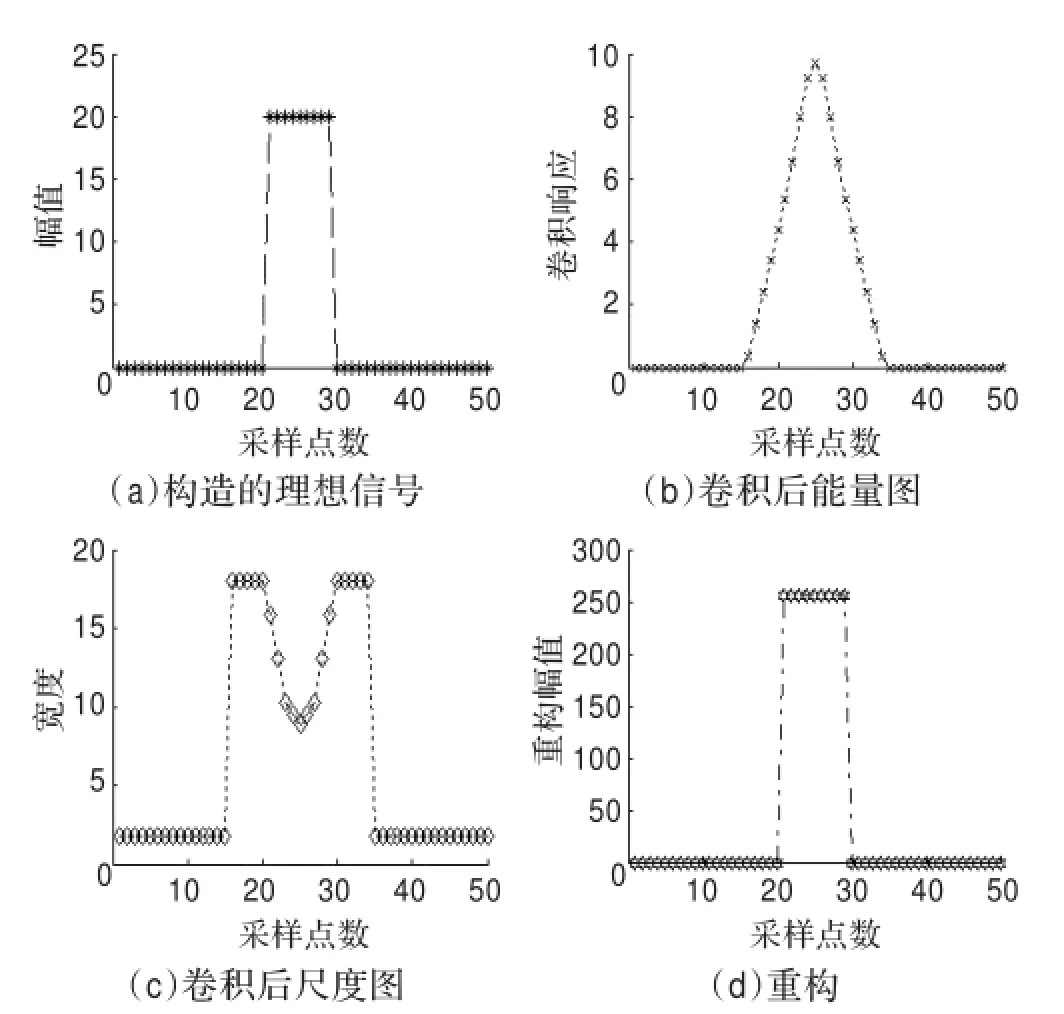
图2 一维理想信号滤波示意图

图2（a）是尺度为9的理想信号，由图（b）可知，信号中心位置的响应结果最大。根据得到的尺度图图2（c），通过公式（4）计算，得到信号尺度为8.38，在误差允许的范围内，计算出来的尺度等于图2（a）信号的尺度。

根据信号的中心位置和尺度重构出原始信号：中心位置左右各一半尺度范围内的点赋大小为255的值，重构结果如图2（d）所示。

空间补偿σ2并不是唯一的，Luo Gang等在文献[14]中对高斯二阶导数滤波器的空间补偿进行了讨论。空间补偿的不同影响线条尺度与滤波器尺度之间的比例关系，但并不影响在线条中心处取得全局最大响应这个事实。

2.3 二维线条重构

在重构二维线条特征时，不仅要考虑中心点位置和尺度，还要考虑线条的角度，即线条在图像中的走向。各向同性的滤波器不能满足要求，必须构造出有角度信息的滤波器。本文的方法是以滤波器中心点为中心对零度（水平方向）高斯-拉普拉斯滤波器做一系列角度的旋转，得到不同角度的滤波器，图3给出了滤波器示意图。

图3是在σ=5.1，θ=60°时滤波器三维示意图。图4是一组在不同尺度(σ)，不同角度(θ)下的二维滤波器。

线条检测的第一步是利用多尺度、多角度的高斯-拉普拉斯滤波器对原图像做卷积，能量图是卷积响应的全局最大值：

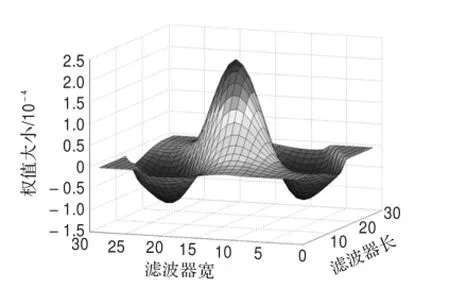
图3 滤波器三维示意图

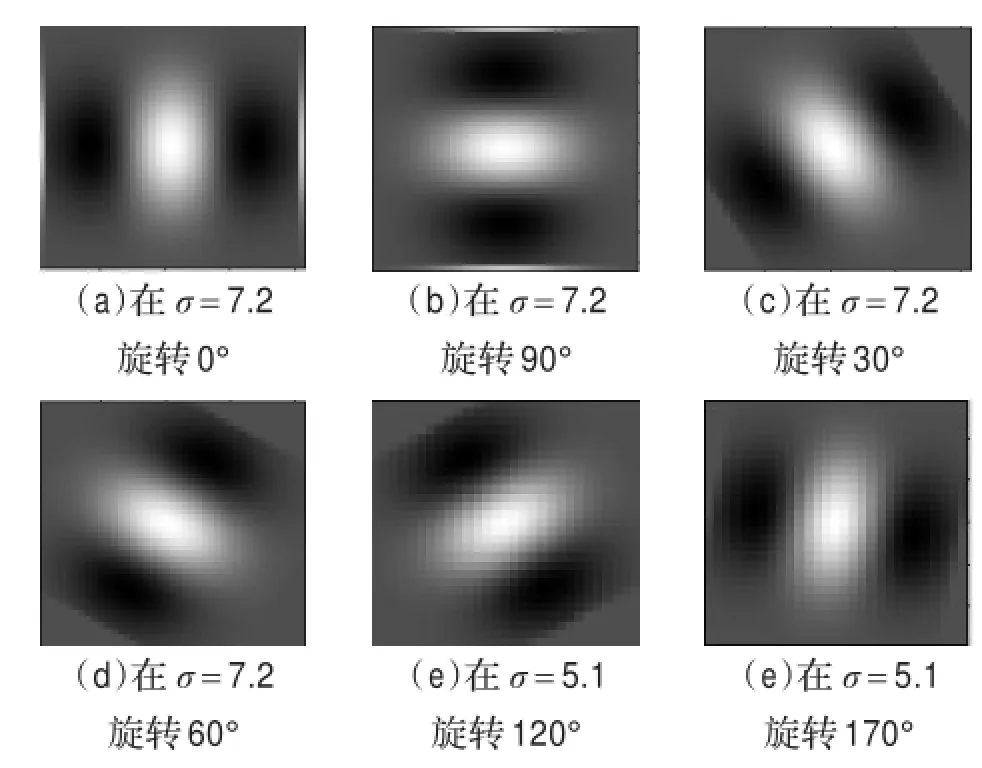
图4 滤波器示意图

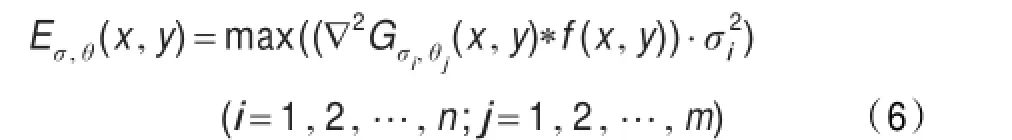
其中，n和m分别代表尺度和角度的个数。

线条的尺度图与角度图是原图中各个像素在所有尺度与角度下卷积响应取得全局最大值时分别对应的尺度与角度组成的图像。

当滤波器与线条完全匹配时，线条的卷积响应在当前尺度与角度下取得全局极值，而且在线条的中心位置形成局部极值，根据这个特性本文采取非极大值抑制和双阈值处理对线条的中心线进行提取。通过对应的尺度图和角度图得到线条的尺度和角度信息。最后对线条进行重构，即中心线图的每个中心线点在其法线方向上画出长度为线条尺度且像素值为255的有向线段。

3 线条重构算法流程

前面讨论了滤波器的构造以及空间补偿问题，接下来分析整个线条重构过程。首先给出本文的算法整体流程图，见图5。

3.1 多尺度滤波

尺度σ最小值选取为0.8，最大值的选取满足线条检测需要即可。本文动态选择步长：当σ较小时，步长较小，随着σ的不断增大，步长逐渐增大。角度设定以步长为5从0°到180°，这样做的时间复杂度较大，文献[7]中提到的解决方案是利用Hessian矩阵计算角度。图6是二维滤波过程示意图。

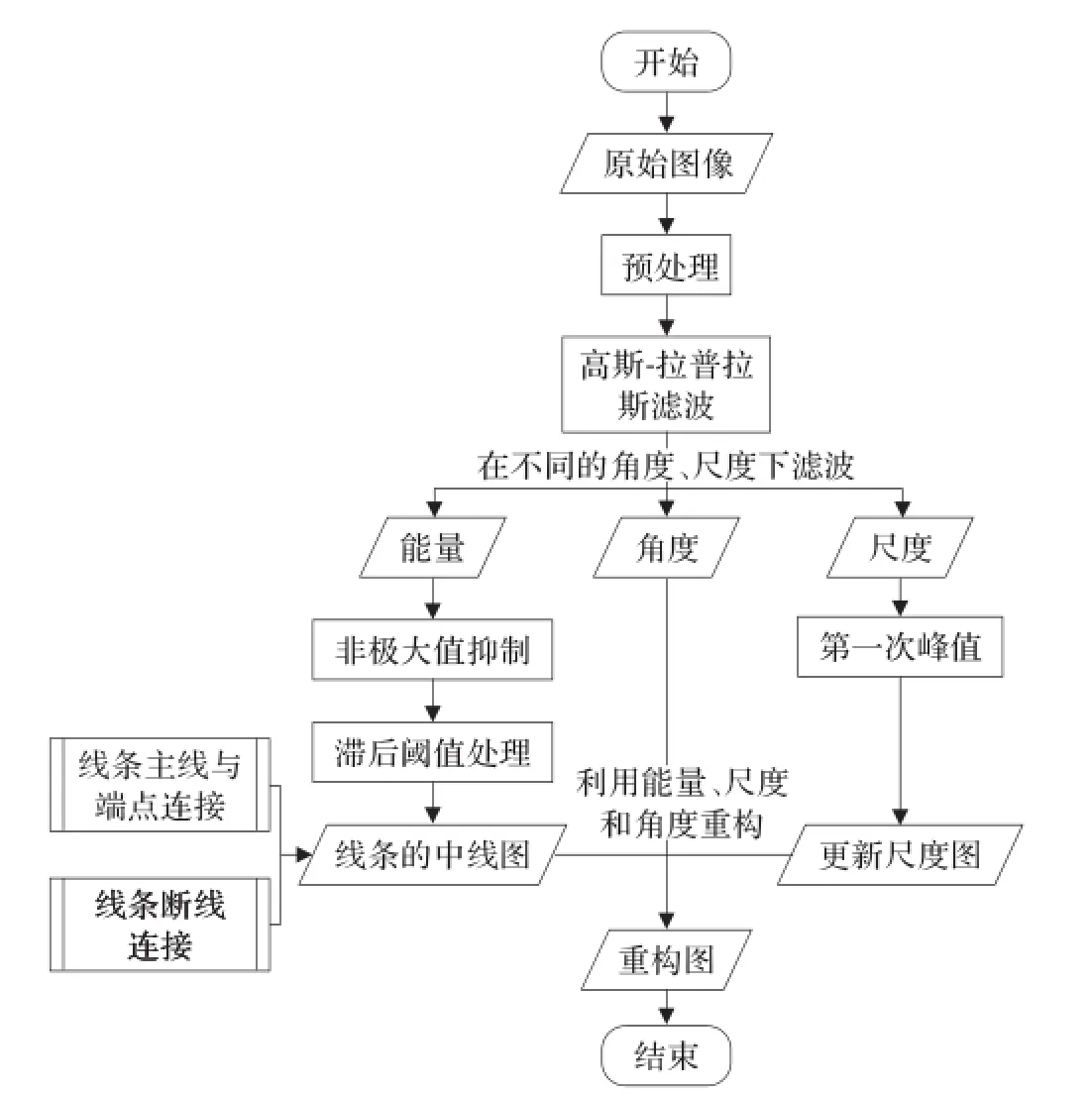
图5 本文整体算法流程图

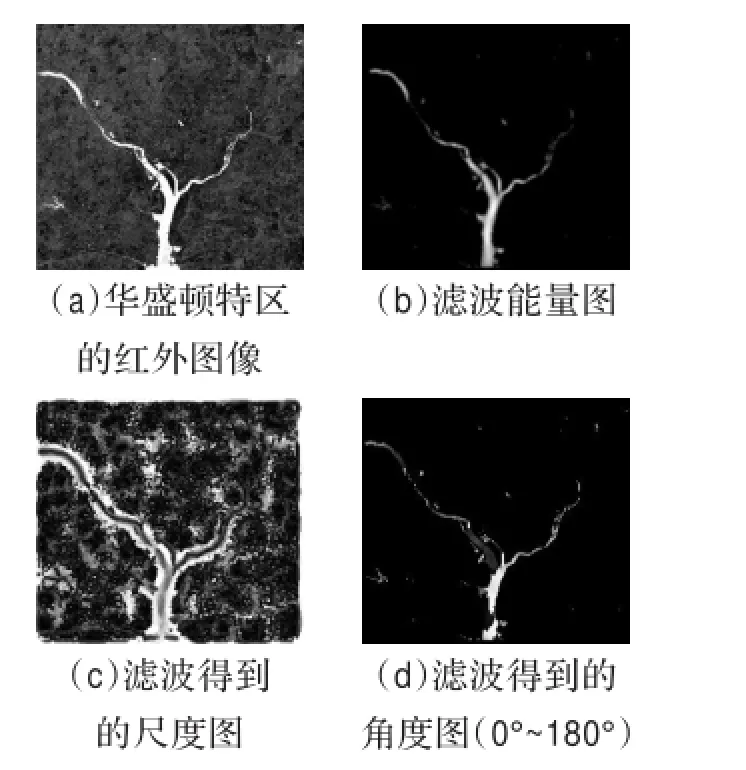
图6 二维滤波过程示意图

分析图6可知，（b）表明只有在线条（河流）部分能取得较大能量，且在线条中心处形成峰值，背景平滑区域的响应值较小，（c）中线条部分的灰度与尺度成正比，（d）图中，在没有考虑线条矢量角度的情况下并不能区分0°和180°。

3.2 中心线提取

提取中心线的算法本文采用Canny算法[8，15]中的非极大值抑制以及滞后阈值处理。滤波得到线条的方向在0°～180°之间，还不能完全刻画线条的走向，需要将原来的线条方向归并编号成八链码信息，如图7。

3.2.1 断线连接

比较细弱的线条在中心线提取后会引起断线的现象。另外，在线条的交叉部分也会出现中心线不连续的情况，所以连接算法还包含了交叉点的连接。

图7 矢量角示意图

首先，对中线图的二值图像进行连通域标记。断线连接需要用八链码信息，利用这样的规则进行断线连接：

（1）确定断线的端点，端点是线条中心线的尾端。（2）在同一个连通域的端点认为是同一个线条，不考虑连接。

（3）对于不在一个连通域的端点，如果距离不超过3像素，不考虑端点的矢量角，直接连接。

（4）对于距离大于3像素且小于8像素的端点需要考虑它们的矢量角方向，只有矢量角方向相反的端点才连接。

3.2.2 交叉区域连接

断线连接结束后，利用这样的规则连接交叉点部分：

（1）对于不是端点的中心线点，在其尺度范围内寻找端点。

（2）如果只找到一个端点且方向不和当前非端点方向平行，就将当前点和端点连接。

（3）如果当前非端点在其尺度范围内找到多个端点，那么距离最短的且方向不平行于当前点的端点符合连接要求。

连接算法效果如图8所示。

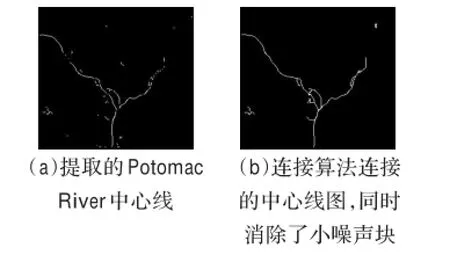
图8 连接算法效果

3.3 线条重构

两个线条距离较近或者线条的双侧或单侧有遮挡，以及边界、噪声等都会对线条尺度的计算带来误差。本文只讨论线条两侧有比较对称的干扰时的尺度调整。采取的方法是多尺度、多角度滤波时如果卷积响应的第一次峰值出现时的尺度与全局最大值响应时的尺度差异明显时，就选取第一次峰值出现时的尺度作为线条真正的尺度。

通过上述一系列处理，最后去除短线条，得到图9的重构图。

图9 （a）重构图

图9 （b）重构图局部放大

4 实验结果与分析

图10中的（a）和（d）分别选取大小为512×340和512×512，8比特的科罗拉多河和华盛顿特区的遥感图像为实验对象。因为本文研究暗背景上检测重构亮线条，所以对高斯-拉普拉斯有一次取反过程，对原始图像也有一次取反过程。在预处理阶段，选取大小5×5的高斯平滑模板对原图进行平滑。多尺度、多角度高斯-拉普拉斯滤波后，将能量图线性压缩到0～255。提取中心线时的双阈值处理的大小阈值本文分别选取50和20，对于不同的实验，大小阈值可做调整。

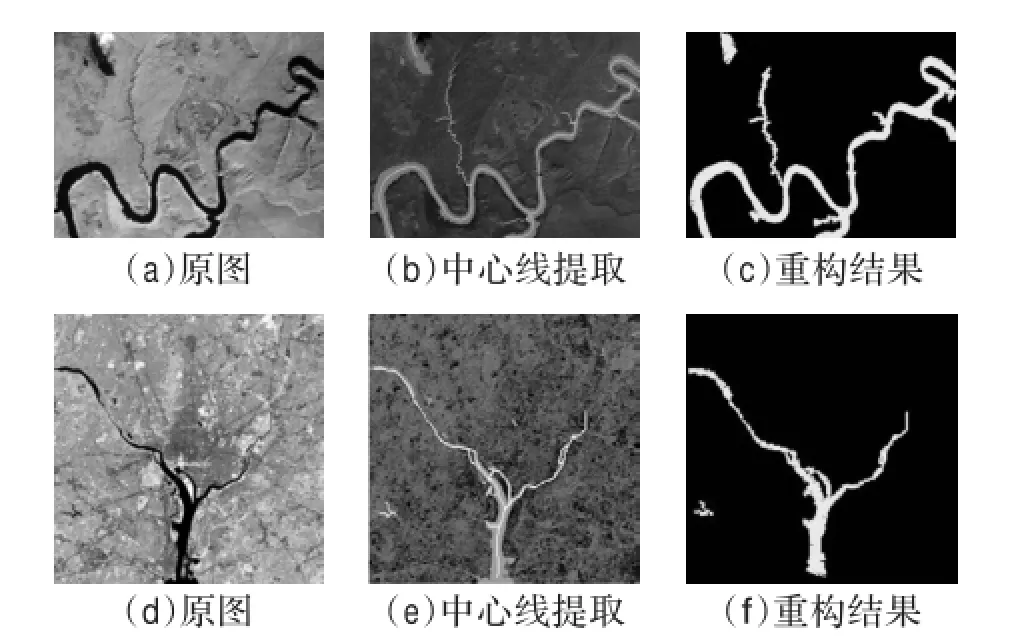
图10 中心线提取及重构结果

图10（b）（e）是中心线提取结果，（c）（f）是重构结果。从（b）观察到，河流偏右的竖直部分被桥梁隔断，利用本文的线条连接算法可以将河流中心线连接起来，但（c）重构结果可以看到，此处的尺度明显有误，类似的错连现象还有在（e）图中的右侧河流分叉部分。对于存在相互干扰的线条以及细弱线条的检测重构能力较差。河流交叉处，中心线提取以及重构有些失真，这是匹配模板的天生缺陷。

图11中（a）（b）分别为人工勾画的图10中（a）（d）的线条，（c）（d）中最亮的部分表示本文算法重构的线条与人工勾画线条的重合部分，即正确重构的部分；最暗的部分表示错误重构的部分；较亮的灰色部分为漏重构部分。通过对本文重构结果与人工勾画线条图像的像素统计，得到表1的测度。

分析图11中的（c）（d），本文算法重构结果的线条尺度大都比实际线条的尺度略小，原因是本文假定线条模型为公式（1）的形式，而实际图像的线条一般都会退化。

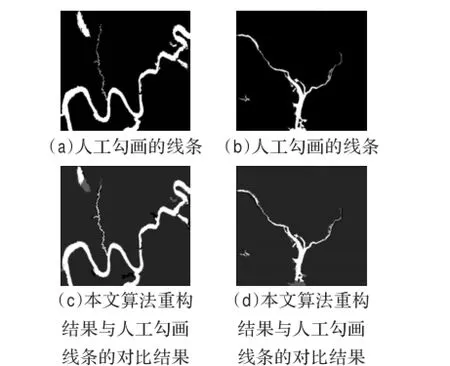
图11 本文算法重构结果与人工勾画线条的对比结果

表1 本文重构结果与人工勾画线条对比（%）

线条曲率变化剧烈的区域，本文算法重构的失真较大，如科罗拉多河支流部分和华盛顿特区图像左下角的湖。华盛顿特区图中河流部分的最下面和科罗拉多河图左上角的核电站因为尺度较大且靠近图像边缘，出现了重构失真情况。排除这些失真较大的重构情况，重构线条的正确率进一步提升，如表2所示。

表2 排除较大失真的重构结果与人工勾画线条对比（%）

对于这种对比度较为明显的线条，利用本文重构算法能比较准确地重构出来。重构出图像中的线条，对后续计算机视觉的图像理解有很大的帮助。

5 结束语

本文通过对基于多尺度空间的高斯-拉普拉斯的线条检测重构进行了理论分析，同时探讨了多尺度空间的补偿问题，结合线条的尺度和角度信息实现了线条的重构。对于不明显和干扰较大的线条特征，人类视觉系统可以轻而易举地辨认，计算机想要做到这一点显然比较困难，展望以后的工作，要想完成对任意线条实现检测重构，需要把研究重点放在较弱、较细以及干扰较大的线条检测重构上。

[1]Steger C.An unbiased detector of curvilinear structures[J]. IEEE Trans on Pattern Analysis and Machine Intelligence，1998，20（2）：113-125.

[2]Jang J H，Hong K S.Detection of curvilinear structures and reconstruction of their regions ingray-scale images[J]. Pattern Recognition，2002，35（4）：807-824.

[3]Hoover A，Kouznestsova V，Goldbaum M.Locating blood vessels in retinal images by piecewise threshold probing of a matched filter response[J].IEEE Trans on Medical Imaging，2000，19（3）：203-210.

[4]Chen Bin，Zhong Hua.Line detection in image based on edge enhancement[C]//Second International Symposium on Information Science and Engineering（ISISE），2009：415-418.

[5]Qian Xiaoning，Brennan M P，Dione D P，et al.A nonparametric vessel detection method for complex vascular structures[J].Medical Image Analysis，2009，13（1）：49-61.

[6]Li Shuxiao，Chang Hongxing，Zhu Chengfei.Fast curvilinear struture extraction and delineation using density estimation[J].Computer Vision and Image Understanding，2009，113（6）：763-775.

[7]Obara B，Fricker M，Gavaghan D，et al.Contrast-independent curvilinear structure detection in biomedical images[J]. IEEE Trans on Image Processing，2012，21（5）：2572-2581.

[8]Canny J.A computational approach to edge detection[J]. IEEE Trans on Pattern Analysis and Machine Intelligence，1986，8（6）：679-698.

[9]Lindeberg T.Scale-space：a framework for handling image structures at multiple scales[C]//Proceedings of the Conference，1996：8-21.

[10]Lindeberg T.Scale-space for discrete signals[J].IEEE Trans on Pattern Analysis and Machine Intelligence，1990，12（3）：234-254.

[11]Lindeberg T.Scale-space theory：a basic tool for analyzing structures at difference scales[J].Journal of Applied Statistics，1994，21（2）：224-270.

[12]Lowe D G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision，2004，60（2）：94-110.

[13]Mikolajczyk K，Schmid C.An affine invariant interest point detector[C]//European Conference on Computer Vision（ECCV），2002：128-142.

[14]Luo Gang，Chutatape P，Krishnan S M.Detection and measurement of retinal vessels in fundus images using amplitude modified second-order Gaussian filter[J].IEEE Trans on Biomedical Engineering，2002，49（2）：168-172.

[15]Nixon M S，Aguado A S.特征提取与图像处理[M].3版.北京：电子工业出版社，2010：103-109.

FAN Shunli,LUO Xiaohui

School of Mathematics and Computer Engineering,Xihua University,Chengdu 610039,China

Aiming to lines reconstruction and understanding in images,this paper puts forward maximum energy response by Laplace filter of Gaussian with multi-scale and multi-angle.It adaptively enhances the lines based on multi-scale space theory.Meanwhile it obtains lines scale,angle information and achieves lines detection using on-maximum suppression. Using lines scale and angle information acquired,the lines are reconstructed at last.The experiment results indicate the validity of lines reconstruction algorithm.

multi-scale analysis;lines detection;lines reconstruction

针对图像中线条的重构与理解，基于多尺度空间理论，提出通过多尺度、多角度高斯-拉普拉斯滤波的最大能量响应，对线条进行自适应增强，同时获取线条的尺度、角度信息，利用非极大值抑制对线条实现检测，利用已获取的线条尺度与角度信息对线条进行重构。实验结果表明该线条重构算法的有效性。

多尺度分析；线条检测；线条重构

A

TP391.41

10.3778/j.issn.1002-8331.1210-0268

FAN Shunli,LUO Xiaohui.Lines reconstruction based on multi-scale analysis method.Computer Engineering and Applications,2014,50（18）：188-192.

四川科技厅支撑计划项目（No.2012GZ0019）；四川省高校重点实验室开放研究基金资助项目（No.szjj2011-022）；四川省网络智能信息处理高校重点实验室基金项目（No.SGXZD1002-10）。

樊顺利（1987—），男，硕士研究生，研究领域为数字图像处理、计算机视觉；罗晓晖（1970—），通讯作者，男，博士，副教授，研究领域为计算机视觉、图像识别。E-mail：lxh10801@163.com

2012-10-26

2013-01-25

1002-8331（2014）18-0188-05

CNKI网络优先出版：2013-03-26，http://www.cnki.net/kcms/detail/11.2127.TP.20130326.1042.015.html