关于WDM双环网络网络负荷的研究

李颖，陈业斌

1.安徽省马鞍山师范高等专科学校，安徽马鞍山 243041

2.安徽工业大学计算机学院，安徽马鞍山 243002

关于WDM双环网络网络负荷的研究

李颖1，陈业斌2

1.安徽省马鞍山师范高等专科学校，安徽马鞍山 243041

2.安徽工业大学计算机学院，安徽马鞍山 243002

波长资源是WDM（Wavelength Division Multiplexing）[1]光网络中的稀有资源，虽然在实验环境中可用波长将近有300个左右，但在实用环境中可用波长不到64个，因此WDM网络要解决的基本问题就是如何合理、有效地使用波长，即路由和波长分配问题。网络负荷是网络在完成业务需求集合的前提下，网络通信所需波长数目的下界，这个参数用于衡量可用波长资源的消耗情况，也是路由选择需要考虑的重要因素之一。因此网络负荷一直是光网络的研究重点。

光网络模型可用有向图G(V，E)表示，节点集和边集分别表示为V(G)、E(G)[2]。节点u、v之间有一条链路，当且仅当u、v之间有一条边。从节点x到y的光路径或路由记作P(x，y)，是指从节点x至y的有向传输路径[2-3]。光网络中信息是通过每条链路中所容纳的波长来承载的。节点u需将信息传送到v，称作u、v之间的业务需求（Request），记作R(u、v)。要完成u、v之间的业务需求就需要在u、v间建立光路径。用R表示网络节点间业务需求的集合，一般而言，网络中的业务需求可统一表示为一个节点到其他相异节点对之间的业务需求的集合。在光网络中有关链路负荷的概念定义如下：

定义1[4]链路e在路由集R中的负荷，指R中通过链路e的路径数目，记为η(G，R，e)。最大的链路负荷称为网络负荷，记为η(G，R)，容易得到：

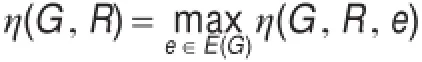
最小的满足需求集的弧负荷称作图G在需求R下的最优弧负荷，记为η(G)。容易得到：η(G)=minη(G，R)。

目前，大多有向双环网络采用光波来传送信息，因此，本文以有向双环网络的拓扑结构为基础来研究光网络负荷的相关问题。

1 有向双环网的网络负荷

近年来，关于有向双环网络的研究主要集中在网络直径、路由算法、最小路径图和最优步长等问题上。Wong和Coppersmith[5]证明了有向双环网络的直径存在下界。该结论给人们寻找最优双环网络提供了理论依据。Chen[6-8]证明了有向双环网络最小路径图——L-型瓦的存在，并给出了求L-型瓦相关参数的定义。有了L-型瓦，使得与距离相关的问题的研究变得更加方便。接下来，人们又对有向双环网络的最优步长问题进行了研究[9-11]，发现了步长与紧优双环网络之间的关系[12-15]。关于双环网络的网络负荷方面的研究，目前还没有见到相关文献。

有向双环网络的图论模型是指这样一个有向图G(N;r，s)[5]，如图1所示。N、r、s是自然数，其中N是网络节点的个数，r、s是步长，且1≤r≠s＜N。节点集V={0，1，…，N-1}，边集为E={v→v+r(modN)，v→v+s(modN)|v∈V}。从每个节点v发出两条有向边v→v+r(modN)和v→v+s(modN)，称v→v+r(modN)形式的边为[+r]边，v+s(modN)形式的边为[+s]边，其中x(modN)是x除以N所得非负余数。从定义可知，对于给定的N、r和s，唯一决定了一个有向双环网络G(N;r，s)的结构，因而也决定了它的相关特性。

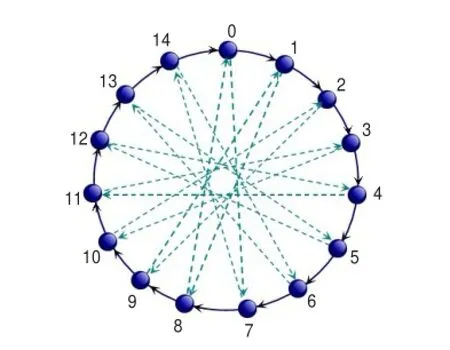
图1 有向双环网络G(15;1，7)的拓扑结构

根据有向双环网络G(N;r，s)的对称性，节点v到任意节点u之间的路由问题可转化为节点0到节点u-v之间的路由问题，因此，在有向双环网络中，任意两节点之间的距离问题都可转化为节点0和其他节点之间的距离问题。为了更直观地了解双环网络的结构，根据有向双环网络的路由特性，把双环网络拓扑结构中的所有节点映射到直角坐标系中，其生成算法如下：

在直角坐标系中，令X轴的单位长度定义为r，Y轴的单位长度为s。由X轴、Y轴以及间隔为r的垂直线和间隔为s的水平线将第一象限分隔为多个格点，把第一象限中的所有格点(x，y)按下列顺序排成序列：(0，0)，(r，0)，(0，s)，(2r，0)，(r，s)，(0，2s)，…，(jr，0)，((j-1)r，s)，…，((j-i)r，is)，…，(r，(j-1)s)，(0，js)，…。并且依次在每一格点上安置双环网络G(N;r，s)的节点v∈{0，1，…，N-1}，其中v=xr+ys(modN)。如果在此之前节点v已出现过，则空出此格点，考察下一个格点，直到双环网络G(N;r，s)中所有的节点0，1，…，N-1都已出现或不再产生新的节点为止。生成图形的形状通常为“L”型，故称为L-型瓦[6]。其中四个参数a、b、p和q分别表示L-型瓦四条边上的格点个数。并记L-型瓦为L(N;a，b，p，q)。如G(15;1，7)所对应的L-型瓦如图2所示。

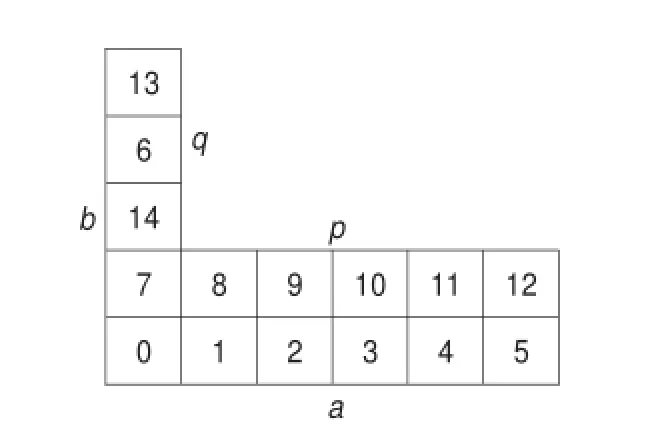
图2 L(15;6，5，5，3)

定义2对于给定N(N≥4)的有向双环网络G(N;r，s)，当r取整数1，s依次取(r，N)中的所有整数值，将得到的一组有向双环网络称为有向双环网络的一个无限族（infinite family），记为IF_G(N)。

有向双环网络只存在两种有向边：[+r]边和[+s]边，根据定义1，对于有向双环网络的网络负荷可以进行如下定义：

定义3用P表示有向双环网络G(N;r，s)最小路径图中一个节点到其他节点间的路径，用η(G，P，e)表示P中所包含的[+r]边和[+s]边的数目，有向双环网络的网络负荷是指所有P中所包含的[+r]边和[+s]边的总数目，记为η(G，e)。因此可得：

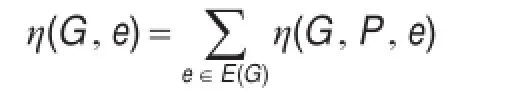
定义4在有向双环网络的一个L-型瓦中，所有[+r]边负荷记为η(G，e+r)，所有[+s]边负荷记为η(G，e+s)，若η(G，e+r)=η(G，e+s)，则称有向双环网络G(N;r，s)的边负荷是平衡的。

在有向双环网络G(N;r，s)的一个IF_G(N)中，由于不同步长的网络所对应的L-型瓦是不同的，因此，其网络负荷也不同。完成相同的业务需求所经过的边越少，其网络的通信效率越高，因此，边负荷越小的网络性能越好。如何才能计算出有向双环网络的网络负荷，根据定义3和定义4可知，有向双环网络的网络负荷也是一个与距离相关的指标，因此，它也可从有向双环网络的最小路径图——L-型瓦中得到解决。方法如下：

定义5设x0，y0是正整数且满足同余方程：xr+ys=v(modN)(v∈{0，1，…，N-1})。则称(x0，y0)是同余方程的正解。若对于同余方程的任意异于(x0，y0)的正解(x1，y1)都有：

（1）x0+y0＜x1+y1

（2）当x1+y1=x0+y0时，有x1＜x0

则称(x0，y0)是同余方程的最小正解。

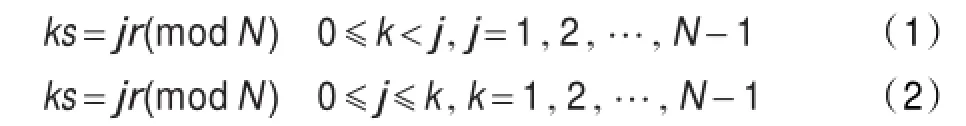
定义6对于给定的有向双环网络G(N;r，s)，同余方程定义如下：定理1对于给定的有向双环网络G(N;r，s)，其最小路径图记为L(N;a，b，p，q)。若同余方程如定义6所定义，且方程（1）的最小正解为(k1，j1)，方程（2）的最小正解为(k2，j2)，则a=j1，b=k2，p=j2，q=k1。

证明（1）根据双环网络G(N;r，s)的L-型瓦定义可知，a是X轴上的最大格点数。定义6中的方程（1）ks=jr(modN)，0≤k＜j，j=1，2，…，N-1所得最小正解(k1，j1)的含义是：从节点0出发，最少走j1个[+r]边就会出现和Y轴上相同的节点。根据L-型瓦的定义，L-型瓦内不允许出现重复节点。因此，从节点0出发，向X轴的正方向只能走j1-1步，每走一步到达一个节点。包括0节点在内，共有j1个节点。所以a=j1；同理在Y轴上可得：b=k2。

证明根据定义3，有向双环网络的网络负荷是指双环网络中一个节点到其他所有节点所要经过的边集。由于L-型瓦为有向双环网络的最小路径图，因此，网络负荷可利用L-型瓦来得到。根据有向双环网络的对称性，只要考虑从节点0到其他所有节点的距离，就能知道有向双环网络的网络负荷，因此，网络负荷可以通过计算L-型瓦中节点0到其他节点的边负荷之和来得到。由于节点0到其他节点的边负荷可以表示为x条[+r]边和y条[+s]边之和(x≥0，y≥0)。因此，可分两个步骤来计算[+r]边和[+s]边的负荷。

（1）计算节点0到其他节点[+r]边的负荷。如图2所示，可将向双环网络G(N;r，s)的L-型瓦分为长为a、宽为b-q和长为q、宽为a-p的两个长方形，分别计算两个长方形中[+r]边的个数，可得下式：

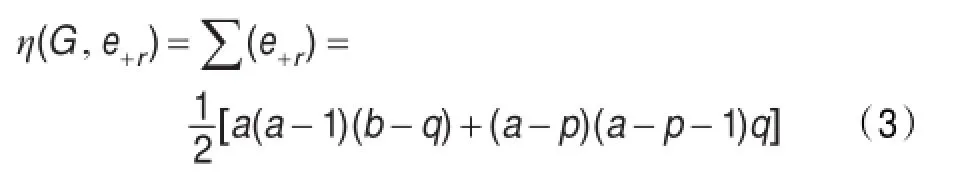
（2）计算节点0到其他节点[+s]边的负荷。如图2所示，可将向双环网络G(N;r，s)的L-型瓦分为长为b宽为a-p和长为p宽为b-q的两个长方形，分别计算两个长方形中[+s]边的个数，可得下式：

由定理1可知，有向双环网络的最小路径图L(N;a，b，p，q)的四个参数可以使用定义6的同余方程直接得出，无需绘制出L(N;a，b，p，q)。用此方法得出四个参数值的算法复杂度比通过绘制出L-型瓦算法的复杂度大大降低。有了L(N;a，b，p，q)的四个参数，根据定理2就能快速地计算出任意N值有向双环网络G(N;r，s)的网络负荷了。

2 实验结果及分析

对于一个业务需求，如何设计一个好的网络结构，使得完成该业务需求的网络负荷最小，即寻找最优负荷网络和平衡负荷网络的分布规律，这是研究网络负荷的最终目标。为了实现这个目标，对多个有向双环网络的无限族进行了仿真实验。实验参数选取如下：

对于有向双环网络G(N;r，s)，N取[4，1 000]内的所有整数值和[1 000，10 000]内的1 000个随机整数值；对于任意N值，r取1，s取(1，N)内的所有整数值，这种取值方式每次都能得到一个完整的无限族。图3所示的是N=40的一个完整无限族的[+r]边的负荷和[+s]边的负荷的分布情况。图4所示的是N=40的一个完整无限族中的网络总负荷的分布情况。根据实验结果分析，不难发现如下一些关系：

（1）对于有向双环网络G(N;r，s)的任意无限族，可能存在多个负荷平衡的网络，如G(40;1，19)、G(40;1，29)和G(40;1，35)都是负荷平衡网络。负荷平衡网络的总负荷通常都比较小，如η(G(40;1，19)，e)=238，η(G(40; 1，29)，e)=204，η(G(40;1，35)，e)=210。其中204是该无限族中最小的网络负荷。但并没有发现负荷平衡网络分布的任何规律。

（2）对于有向双环网络G(N;r，s)的任意一个无限族中，其网络负荷的分布呈轴对称图形。

（3）对于有向双环网络G(N;r，s)的任意一个无限族中，其网络负荷存在一个上界值和下界值，达到下界值的网络称为最优负荷网络。在G(40;1，s)无限族中，G(40;1，12)和G(40;1，29)都是最优负荷网络。如图4所示。

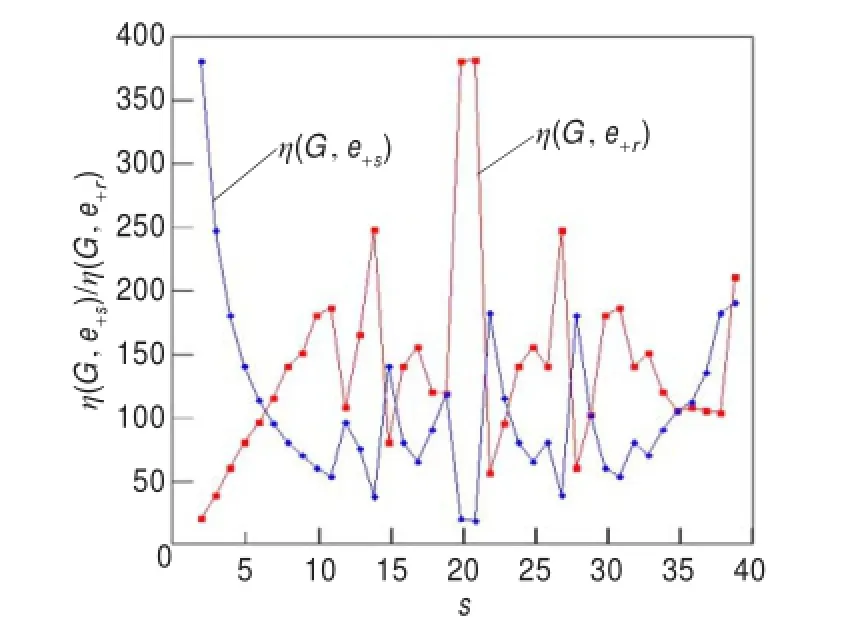
图3 G(40;1，s)的[+r]边的负荷和[+s]边的负荷

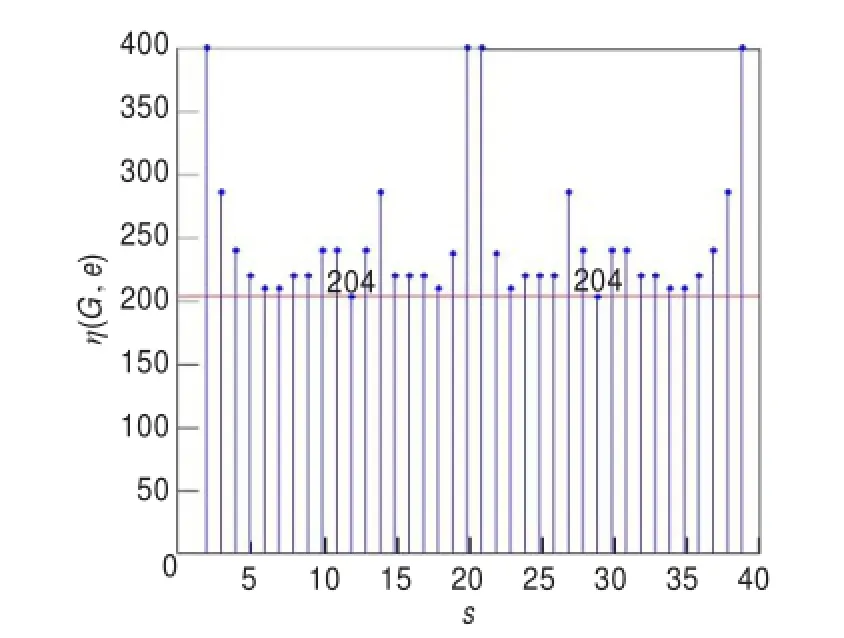
图4 G(40;1，s)的网络负荷分布图

容易求得有向双环网络G(N;r，s)网络负荷η(G，e)的上界值与N的关系：当N为大于4的奇数时，η(G，e)= (N2-1)/4；当N为大于4的偶数时，η(G，e)=N2/4。但网络负荷的下界值与N之间的关系并没有发现，这将是下一个努力的方向。

3 结论

对于给定的有向双环网络G(N;r，s)，通过参数k1、k2、j1和j2的定义，求出G(N;r，s)最小路径图L(N;a，b，p，q)的四个参数值。根据有向双环网络的最小路径图——L-型瓦，给出了计算有向双环网络的网络负荷公式，该公式只与L(N;a，b，p，q)的四个参数相关。通过实验结果的对比分析不难发现：有向双环网络的负荷可分为[+r]边的负荷和[+s]边的负荷，在有向双环网络G(N;r，s)的一个无限族中，可能存在多个负荷平衡的网络。在有向双环网络G(N;r，s)的任意一个无限族中，其网络负荷的分布呈轴对称图形，且网络负荷存在上、下界值，达到该下界值的网络称为最优负荷网络，但该下界值与N之间的关系目前并未发现。该实验结果对于研究网络负荷的意义是显而易见的。网络负荷是否达到或接近最优将成为双环网络设计时考虑的重要因素之一。

[1]Wilfong G，Winkler P.Ring routing and wavelength translation[C]//Proceedings of the 9th Annual ACM-SIAM Symposium on Discrete Algorithms，1998：333-341.

[2]Heydemann M，Meyer J C，Sotteau D.On forwarding indices of networks[J].Discrete Applied Mathematics，1989，23（2）：103-123.

[3]Hou X M，Xu M，Xu J M.Forwarding indices of consistent routings and their complexity[J].Networks，1994，24：75-82.

[4]Gargano L，Vaccaro U.Routing in all-optical networks：algorithmic and graph-theoretic problems[C]//Numbers，Information and Complexity，2000：555-578.

[5]Wong C K，Coppersmith D.A combinatorial problem related tomultimoduleorganizations[J].Journalof Association Computer，1974，21（3）：392-402.

[6]Chen C Y，Hwang F K.The minimum distance diagram of double-loop networks[J].IEEE Transactions on Computers，2000，49（9）：977-979.

[7]Chen C Y，James K L，Tang W S.An efficient algorithm tofindadouble-loopnetworkthat realizesagiven L-shape[J].Theoretical Computer Science，2006，359（1/3）：69-76.

[8]Chen C Y，Hwang F K.Equivalent L-shapes of doubleloop networks for the degenerate case[J].Journal of Interconnection Networks，2000，1：47-60.

[9]Chan C F，Chen C Y，Hong Z X.A simple algorithm to find the steps of double-loop networks[J].Discrete Applied Mathematics，2002，121（1/3）：61-72.

[10]李颖，陈业斌.有向双环网络G(N;r，s)的寻径策略[J].华中科技大学学报：自然科学版，2009，37（5）：45-48.

[11]林宣治，陈宝兴.关于有向双环网络L-形瓦的四个参数[J].漳州师范学院学报：自然科学版，2006，33（2）：12-16.

[12]陈业斌.基于二叉树的有向双环网络最优路由算法[J].华中科技大学学报：自然科学版，2008，36（6）：43-46.

[13]方木云，赵保华，屈玉贵.双环网络G(N;1，s)的L形瓦仿真算法[J].系统仿真学报，2005，17（4）：914-916.

[14]Gomez D，Gutierrez J，Ibeas A.Optimal routing in double loop networks[J].Theoretical Computer Science，2007，381（1/3）：68-85.

[15]Chen Y B，Li Y，Wang J K.On the wide diameter of directed double-loop network[J].Journal of Network and Computer Applications，2011，34（1）：692-696.

LI Ying1,CHEN Yebin2

1.Ma’anshan Teacher’s College,Ma’anshan,Anhui 243041,China
2.School of Computer Science,Anhui University of Technology,Ma’anshan,Anhui 243002,China

Based on analyzing the structure feature of WDM networks,this paper chooses some representative directed double-loop networks to study.It also provides the solutions of some congruence equations to compute the parameter values of L-shaped tile.According to the structure of L-shaped tile,it provides a formula to compute its network load.The experiment results demonstrate that there may be many load-balanced networks.For anyone of infinite families forG(N;r，s),the distribution of loads is axis symmetric figure,and there is a upper bound and a lower bound for loads.The network is called optimal load network when its load equals the lower bound.These results are important to design optimal double networks and improve transmission efficiency about networks.

Wavelength Division Multiplexing（WDM）networks;directed double-loop networks;network load;L-shaped tile;shortest path;infinite family

针对WDM网络的结构特征，选择具有代表性的有向双环网络G（N；r，s）进行研究。给出一组同余方程，用于快速计算其L-型瓦图的四个参数。根据L-型瓦的结构，给出了计算有向双环网络的网络负荷公式。实验结果分析表明：有向双环网络的一个无限族中可能存在多个负荷平衡的网络。对于有向双环网络G（N；r，s）的任意一个无限族中，其网络负荷的分布呈轴对称图形。网络负荷存在上界和下界，负荷达到下界值的网络称为最优负荷网络。该研究成果对于设计最优双环网络和提高网络通信效率起到决定性的作用。

波分复用（WDM）网络；有向双环网络；网络负荷；L-型瓦；最短路径；无限族

A

TP393.14

10.3778/j.issn.1002-8331.1210-0208

LI Ying,CHEN Yebin.Research on network loads of WDM double-loop networks.Computer Engineering and Applications,2014,50（18）：122-125.

国际科技合作项目（No.2011DFB61530）；安徽省高校级自然科学基金资助重点项目（No.KJ2012A262，No.KJ2013A058）。作者简介：李颖（1971—），女，教授，研究方向为计算机网络及数据库。

2012-10-19

2013-02-05

1002-8331（2014）18-0122-04

CNKI网络优先出版：2013-02-28，http://www.cnki.net/kcms/detail/11.2127.TP.20130228.1148.008.html