基于随机优势关系的区间值信息系统

段晶晶，魏立力

宁夏大学数学计算机学院，银川 750021

基于随机优势关系的区间值信息系统

段晶晶，魏立力

宁夏大学数学计算机学院，银川 750021

1 引言

粗糙集理论是波兰数学家Pawlak Z.于1982年提出的一种数据表达和分析的数学工具[1]，粗糙集理论的主要思想是利用已知的知识库，将不精确或不确定的知识用已知的知识库中的知识来（近似）刻画。该理论与其他处理不确定和不精确问题理论的最显著的区别是它无需提供问题所需处理的数据集合之外的任何先验信息，所以对问题的不确定性的描述或处理可以说是比较客观的，由于这个理论未能包含处理不精确或不确定原始数据的机制，所以这个理论与概率论，模糊数学和证据理论等其他处理不确定或不精确问题的理论有很强的互补性[2-5]。

经典粗糙集理论只针对属性值已知并且单一的情况，即完备的信息系统。然而在现实生活中存在大量属性值未知、缺失、模糊、不精确、不惟一的情形。因此，现有大量文献对这些问题进行深入讨论，提出了不完备信息系统[6]（文献[6]中利用数据补充的方法把不完备区间值信息系统转化为完备的区间值信息系统，即区间端点的缺失值用对应属性的所有属性值的最小下界或最大上界来代替），区间值信息系统[6-8]（文献[7]在区间值信息系统中定义了可能概率，并在可能概率的基础上定义了α-优势关系，给出了基于α-优势关系的扩充粗糙集模型；文献[8]用新的方法定义了α-优势关系，采用相对熵最优赋权准则建立了α-优势关系的概率粗糙模型），集值信息系统[9]（文献[9]提出了析取集值有序信息系统和合取集值有序信息系统，并给出了这两种信息系统的属性约简方法）等粗糙集的扩充模型。其次，考虑到信息偏好有序，最早由Greco等人于1998年提出了基于优势关系的粗糙集方法（DRSA）[10]。利用优势关系建立序信息系统有助于处理连续属性和偏序关系的问题。相对于经典粗糙集理论的基本概念，优势关系替代了不可辨识关系，推动了粗糙集理论的发展，构成了不同的优势关系概念，并形成了一些应用研究[6-11]。

然而利用优势关系对属性域进行排序的结果以一定概率成立，得到的决策规则也以一定的概率成立。所以有序信息系统缺少属性值区间上的概率分布信息。概率信息的丢失将导致建立对象之间的优势关系不符合实际情况，所以要建立一种体现属性值区间上的概率分布信息的信息系统。由于随机优势关系是定义在分布函数上的一种特殊的优势关系，因此利用随机优势关系来研究有序信息系统将是以后研究的趋势。例如文献[11]中就分析了区间值有序信息系统没有蕴含属性值区间上的概率分布信息的缺点，建立了一种基于概率的有序信息系统；文献[12]定义了随机意义下的极小极大损失，给出决策的随机优势粗糙集模型；文献[13]利用近似随机优势准则，提出了近似随机优势度，并对方案排序；文献[14]提出了随机优势指标的概念，并对其合理性和优越性作了论证。

2 随机优势关系

定义1[15]（随机小于）令X和Y分别是两个随机变量，满足：称X随机小于Y，记作X≼SY。

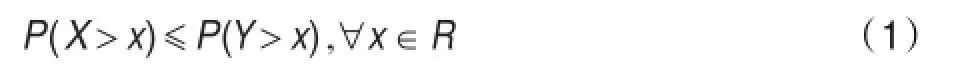
显然上式等价于：

随机优势关系实际上就是定义在概率分布集合上的一个二元关系。

下面先介绍如何在区间值有序信息系统中引入对应属性的概率分布。

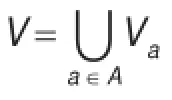
例1表1是高三某班部分同学月考估分情况。

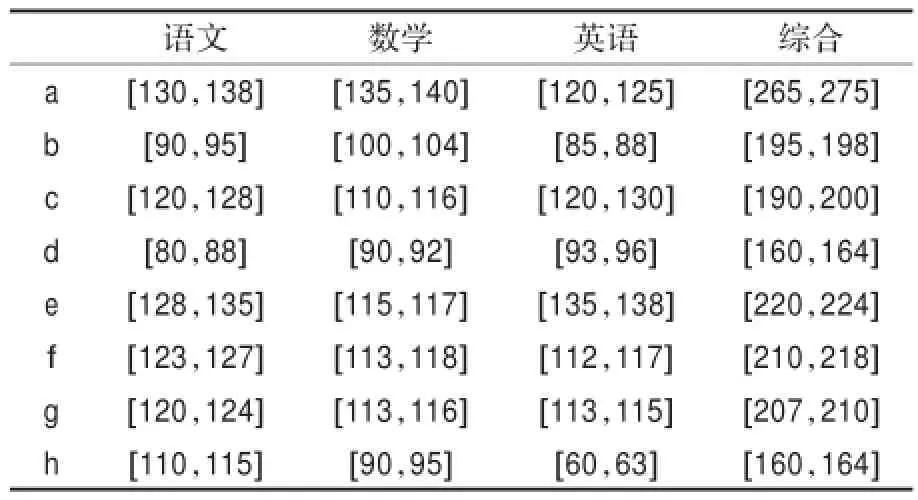
表1 月考估分情况

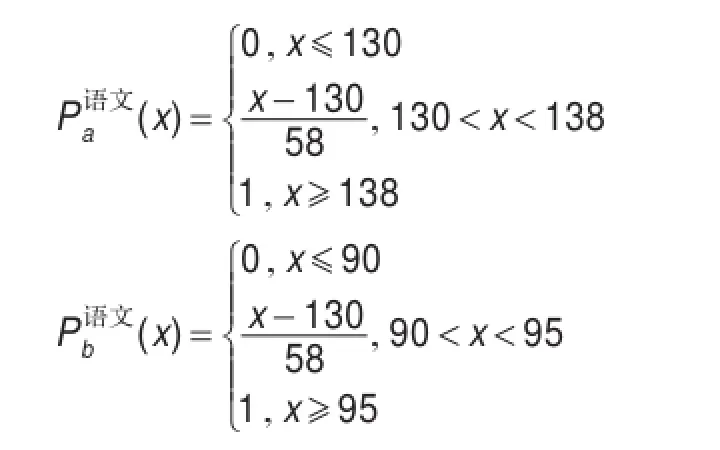
由例1可以看出：

所以，a同学的语文月考成绩要随机优于b。显然，不通过计算也可看出a同学的语文成绩要比b好。

为了叙述简便，以下提到的区间值信息系统均指区间值有序信息系统。

显然，当aL(x)=aU(x)时，f(x，a)退化成单值形式。可见，单值信息系统是区间值信息系统的一种特殊形式。

定义3[11]（区间值有序信息系统）给定区间值信息系统S=(U，A，V，f)，若区间值信息系统S中所有的条件属性都是偏好有序的（即属性值之间存在优劣关系），则称区间值信息系统S为有序信息系统。

定义4（区间值有序信息系统的分布函数）给定区间值有序信息系统S=(U，A，V，f)，对∀a∈A，令Ma= maxi{aU(xi)}，ma=mini{aL(xi)}，则称对象xi在属性a下取值的概率为：

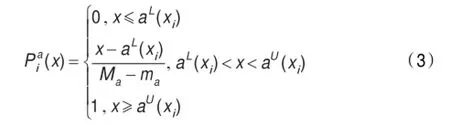
定理2（随机优势的判定定理1）给定区间值信息系统(U,A,V，f)，若aL(xi)≤aL(xj)＜aU(xi)≤aU(xj)(xi，xj∈U，i≠j，a∈A)，则对象xj在属性a下随机优于对象xi。

证明由式（3）可以得到：

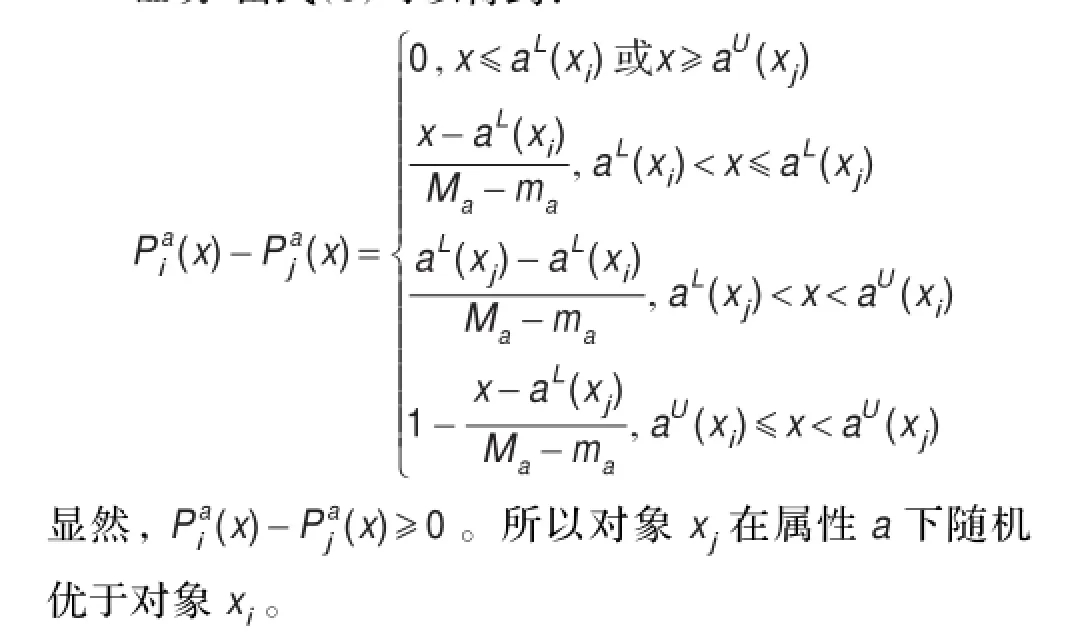
定理3（随机优势的判定定理2）给定区间值信息系统(U，A，V，f)，若aU(xi)≤aL(xj)(xi，xj∈U，i≠j，a∈A)，则对象xj在属性a下随机优于对象xi。

证明同定理2。

3 基于Lévy距离的α-随机优势

文献[8]通过对区间值信息系统进行假设，定义了普通优势关系下各属性对象之间的概率，建立了α-优势关系的概率粗糙模型。本章将利用分布函数这一基本工具，对区间值信息系统进行深入研究，建立α-随机优势关系。

在介绍α-随机优势关系的概念之前，先了解一下Lévy距离的概念。

定义6[16]（Lévy距离）设D={F|F是一维分布函数}，对∀F，G∈D定义：

L(F，G)=inf{ε＞0|F(x-ε)-ε≤G(x)≤F(x+ε)+ε}则L是D上的距离，称为Lévy距离。

定理4[16]（Lévy距离的几何意义）分布函数列G(x)，F(x)之间的最大Lévy距离是2L(F，G)，它的测量沿x轴135°方向。如图1。

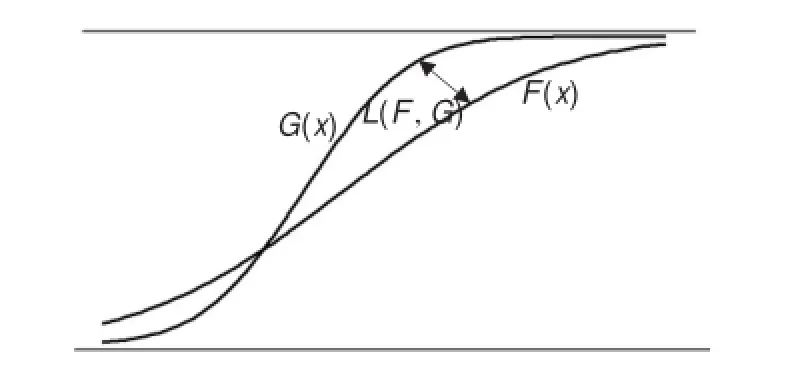
图1 Lévy距离的几何表示图

定义7（α-随机优势）给定区间值信息系统(U，A，V，f)以及属性子集B，L(Fa，Ga)是属性a下对象x和y分别对应的分布函数之间的Lévy距离，α是阈值，称为区间值信息系统的α-随机优势。称

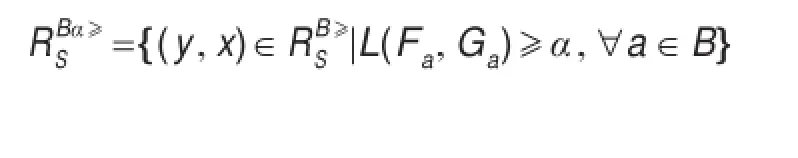
为α-随机优势类。

由α-随机优势关系的定义可以看到，α不仅属于[0，1]这个范围，它还可能比1大。此时的α衡量了两个一维分布函数之间的Lévy距离程度。α越小，两个分布函数越接近，表明对象y随机优于对象x的程度越小；α越大，两个分布函数之间的Lévy距离越大，对象y越是随机优于对象x，作为决策，选择y的可能性就越大。

定理5（α-随机优势关系的性质）给定区间值信息系统(U，A，V，f)，B⊆A，L(Fa，Ga)是对象x和y之间的Lévy距离，则

证明（1）～（4）由定义可证，证明略。（5）证明过程类似于定理1（5），略。

利用定理4计算例1的Lévy距离如表2。从表2中可以看到，用随机优势关系得到元素之间的优劣性，再用Lévy距离衡量元素之间的优势度就不再具有明显的优势关系了。比如，f在数学学科中随机优于g，但利用Lévy距离计算的结果就不再具有随机优势关系了，随机优势度为0。

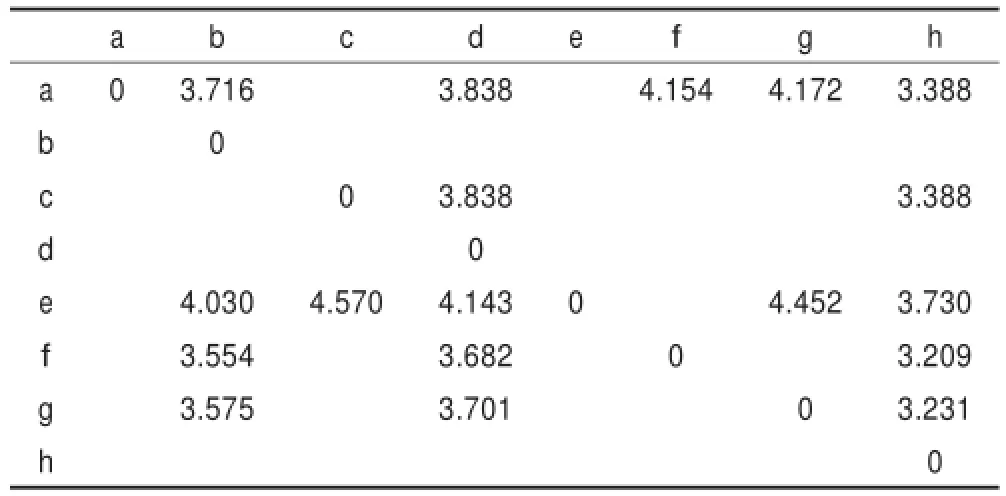
表2 例1的Lévy距离

4 不完备区间值信息系统

如果区间值信息系统里的属性值有未知值时，这样的区间值信息系统就是不完备区间值信息系统。不完备区间值信息系统有三种情形：已知上界，未知下界；已知下界，未知上界；上下界都是未知值。下面就来举例说明不完备区间值信息系统。

例2对于学生成绩，有下面不完备区间值信息系统，如表3。

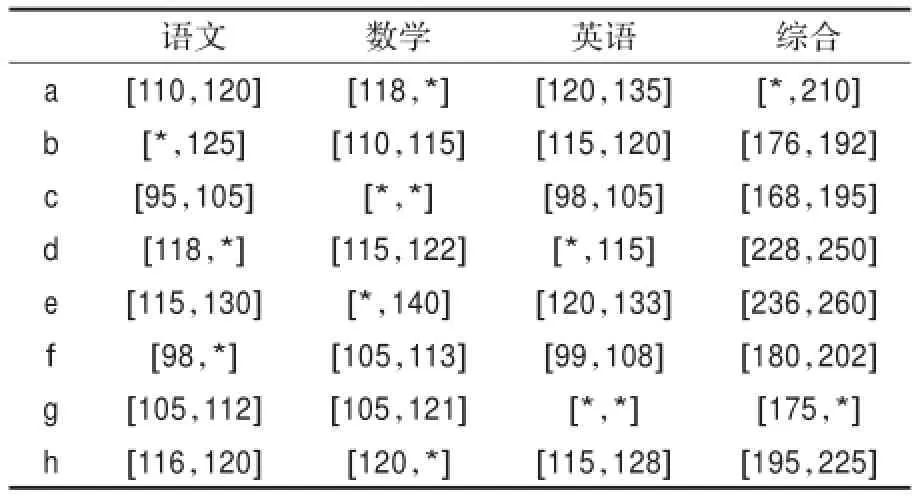
表3 不完备信息系统

例2中“*”表示属性取值的上界或下界未知。在这里未知值是存在的，只不过属性取值的上界或下界缺失。处理这种不完备区间值信息系统的常见方法是把这些未知值补充完整，转化成完备区间值信息系统。这种数据补充的常用方法是求区间端点的平均值。

定义8（区间端点的平均值法）给定不完备区间值信息系统(U，A，V，f)，则填充的不完备区间值信息系统的属性值记为：

其中||aL(U)||，||aU(U)||分别表示属性a下U中属性值不等于*的对象个数。称这种数据补充的方法为求区间端点的平均值法。

表4是经过补充的信息系统。

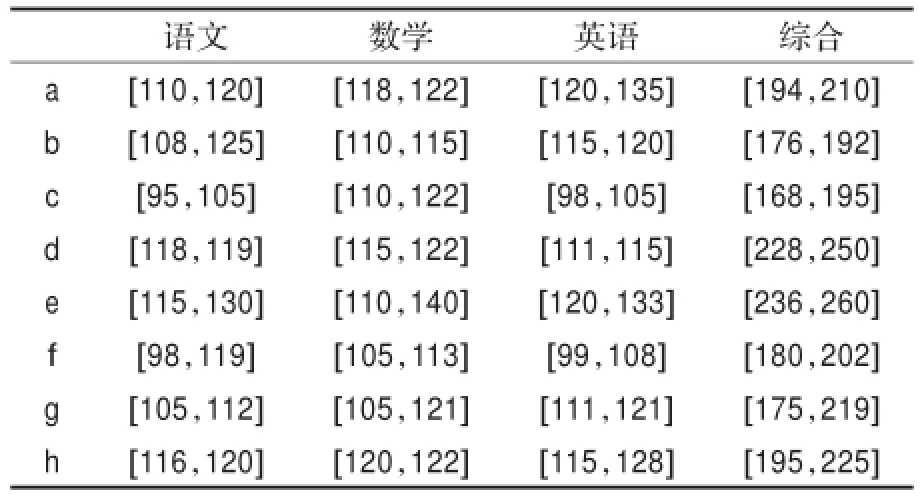
表4 填充的不完备信息系统

表5是例2得出的Lévy距离，得到的随机优势类为：

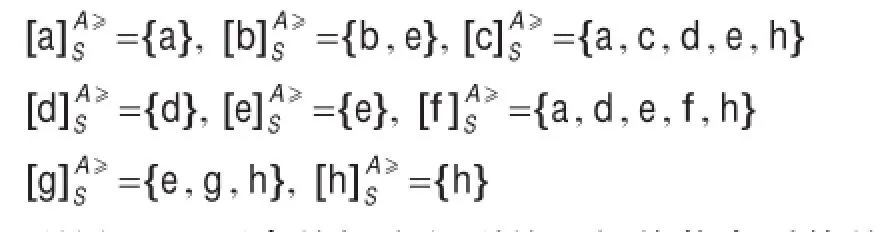
利用Lévy距离的概念得到的区间值信息系统的随机优势类，在整体上反映了对象之间的优劣关系，比对象间点态的优劣比较更具客观性。

当α=5.6时，α-随机优势类为：

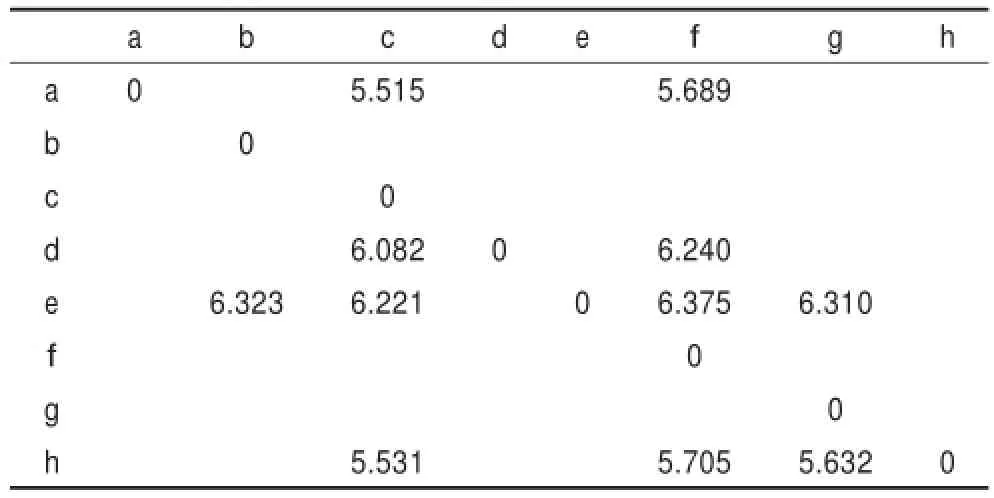
表5 例2的Lévy距离

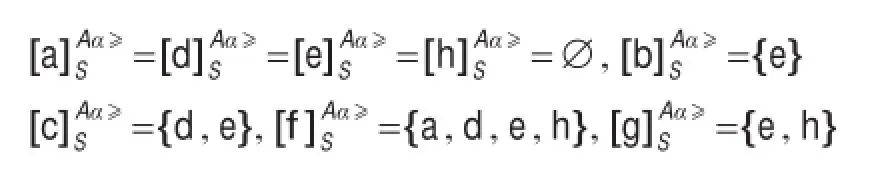
与上面的随机优势类相比较，这里的α-随机优势类是随机优势类的子集，给出了阈值为5.6时的随机优势类。当决策者需要筛选出优势程度不同的对象时，可以调整优势类的阈值，这样可以根据对象间的Lévy距离很容易得到结果。

当α=6.2时，α-随机优势类为：

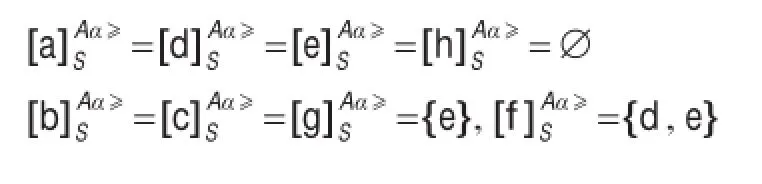
5 结束语

在已有的文献中主要研究了各种基于优势关系的信息系统，没有考虑信息系统本身的概率分布情况。本文讨论了基于随机优势关系的区间值信息系统。首先，在区间值信息系统中引入了分布函数，继而应用随机优势关系的概念，提出了基于随机优势关系的区间值信息系统。由于在分布函数组成的集合中，最为常用的度量之一是Lévy距离，因此，文章在Lévy距离的基础上构造了α-随机优势。最后通过实例进行计算，说明了本文方法的有效性。

[1]Pawlak Z.Rough sets[J].International Journal of Computer and Information Science，1982，11（5）：341-356.

[2]张文修，吴志伟.粗糙集理论介绍和研究综述[J].模糊系统与数学，2000，14（4）：1-12.

[3]王国胤.Rough理论与知识获取[M].西安：西安交通大学出版社，2001.

[4]张文修，梁怡，吴志伟.信息系统与知识发现[M].北京：科学出版社，2003.

[5]张文修，仇国芳.基于粗糙集的不确定决策[M].北京：清华大学出版社，2005.

[6]Yang X B，Yu D J，Wei L H.Dominance-based rough set approach to incomplete interval-valued information system[J].Data&Knowledge Engineering，2009，68：1331-1347.

[7]杨青山，王国胤，张清华，等.基于优势关系的区间值粗糙集扩充模型[J].山东大学学报：理学版，2010，45（9）：7-13.

[8]毛军军，姚登宝，王翠翠，等.α-优势关系下的概率粗糙模型及其在区间数群决策中应用[J].计算机工程与应用，2012，48（18）：48-52.

[9]Qian Y H，Dang C Y，Liang J Y，et al.Set-valued ordered information systems[J].Information Sciences，2009，179：2809-2832.

[10]Greco S，Matarazzo B，Slowińsli R.Rough approximation by dominance relations[J].International Journal of Intelligent Systems，2002，17：153-171.

[11]闫新宝，王国胤，张清华.基于概率的有序信息系统[J].计算机科学，2012，39（1）：239-243.

[12]巩红禹，魏立力.基于粗糙集的随机优势决策方法[J].统计与决策：理论版，2007（16）：60-62.

[13]张尧，樊治平.基于近似随机优势度的随机多属性决策方法[J].东北大学学报：自然科学版，2010，31（9）：1357-1368.

[14]张立清，解林，屠仁寿.随机优势指标方法及其应用[J].控制与决策，1995，10（1）：80-84.

[15]Shaked M，Shanthikumar J G.Stochastic orders[M].New York：Springer，2007.

[16]Huber P J.Robust statistics[M].New York：John Wiley& Sons，Inc，1981.

DUAN Jingjing,WEI Lili

School of Mathematics and Computer Science,Ningxia University,Yinchuan 750021,China

The distribution function is introduced to interval-valued information systems.And the stochastic dominancebased interval-valued information system is proposed.Theα-stochastic dominance relation is constructed in inter-valued information system.Theα-stochastic dominance relation is calculated by the Lévy distance and some numerical examples are shown for the efficiency of the method.

stochastic dominance;interval-valued information system;rough set

在区间值信息系统中引入了分布函数，得到了基于随机优势关系的区间值信息系统，构造了区间值信息系统的α-随机优势关系。利用Lévy距离，对α-随机优势关系进行了计算，实例说明了方法的有效性。

随机优势；区间值信息系统；粗糙集

A

TP18

10.3778/j.issn.1002-8331.1209-0322

DUAN Jingjing,WEI Lili.Stochastic dominance-based interval-valued information systems.Computer Engineering and Applications,2014,50（18）：85-88.

国家自然科学基金（No.11261044）；宁夏高等学校科学技术研究项目。

段晶晶（1987—），女，硕士生，主要研究领域为统计学、人工智能；魏立力（1965—），男，通讯作者，教授，主要研究领域为应用统计与数据分析、人工智能的数学基础。E-mail：weill866@163.com

2012-09-27

2013-01-18

1002-8331（2014）18-0085-04

CNKI网络优先出版：2013-02-07，http://www.cnki.net/kcms/detail/11.2127.TP.20130207.1420.013.html

◎网络、通信、安全◎