分数阶非线性Duffing振子方程的特性研究

李娜

德州学院数学科学学院，山东德州 253023

分数阶非线性Duffing振子方程的特性研究

李娜

德州学院数学科学学院，山东德州 253023

1 分数阶振子方程

实际力学系统中干扰振子振动的因素很多，外界的摩擦力和阻力是产生阻尼的外在原因，另外振子本身在振动过程中也会消耗能量是产生阻尼的内在原因。利用整数阶微分算子来描述黏弹性介质等复杂系统的振子振动时往往会加入一些人为的经验参数来构造非线性微分方程。而引入分数阶微分算子，可以用简单的分数阶微分方程来描述振子的振动。Duffing振子方程是力学中常见的振子方程，在工程技术、物理学，化学以及生物学中都有着广泛的应用[1-2]，Duffing振子的一般形式为：其中l表示阻尼比，m，n分别代表线性与非线性恢复力的系数，f(t)表示外部力。由于Duffing振子的广泛应用，近年来涌现了大量的文献研究Duffing振子的混沌特性，混沌同步问题等[3-4]。本文从另一个角度研究了Duffing振子问题，将Caputo分数阶导数[5-6]：

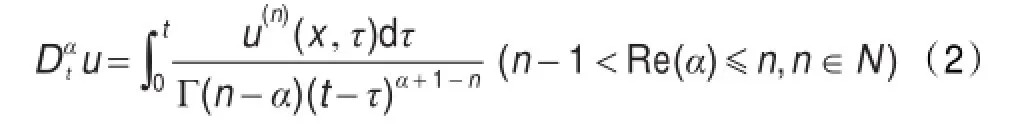
引入到Duffing系统中，Г(·)表示Gamma函数。研究如下一类分数阶非线性的Duffing振子方程：

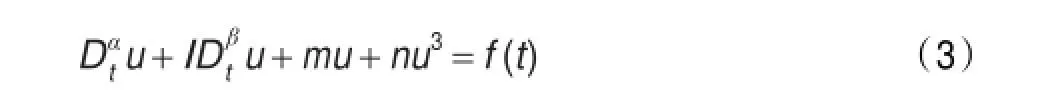
其中1＜α≤2，0＜β≤1分别表示对时间t的α，β阶的Caputo分数阶导数。系统满足初值条件：

关于分数阶非线性系统的求解有很多方法，如积分变换法、格林函数法等解析的方法[7-9]，近年来出现了一些半解析的算法，如Adomian分解法[10-11]、变分迭代法[12-13]、微分变换法[14]等，它们可方便有效地求解大量的线性和非线性问题。这些半解析的方法都存在着内在的一些缺陷，2011年Khan提出一种新的方法[15-16]：同伦扰动变换法，即将同伦扰动法与Laplace变换法两种方法相结合，该方法在一定程度上克服了其他半解析方法存在的缺陷。本文首次将同伦扰动变换法用来求解分数阶的非线性系统并借助Mathematica软件的符号计算功能得到了所研究的分数阶Duffing系统的近似解，最后分析了振子运动与分数阶导数之间的关系。

2 近似解的复杂性研究

首先考虑如下的分数阶非线性Duffing振子方程[17]：

由于级数解比较复杂这里仅列出前三项，其他项可通过Mathematica软件得出，另外每项解中只列出了低幂次的项。从而方程（5）的近似解可以表示为：

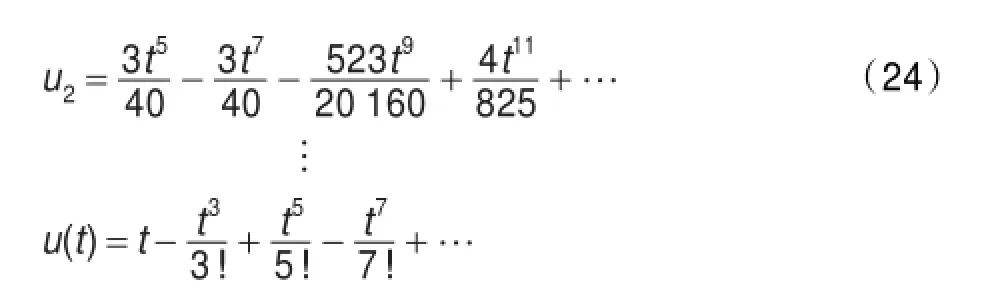
对应的整数阶方程的解u(t)=sin(t)，与文献[17]的结果吻合。从而验证了同伦扰动变换法是一种求解分数阶非线性方程简单有效的方法，提供了一种新的求解分数阶方程的方法。取方程（5）的三阶近似级数解，研究分数阶的振子位移的振动情况如图1。图1给出了振子位移u随分数阶导数α和时间t的三维图像，当分数阶导数α较小时，对振子振动的影响越明显。

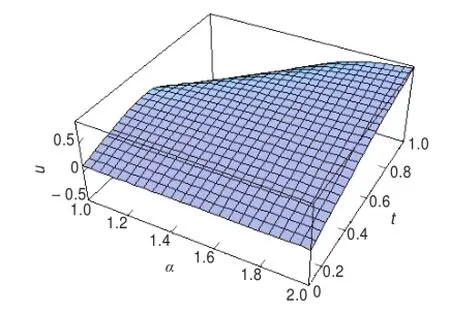
图1 方程（5）的三阶近似解随分数阶导数α和时间t的振动情况

再者为研究阻尼振子方程振动与分数阶导数之间的关系，如在黏弹性介质中的阻尼振动等，阻尼项一般可用分数阶微积分进行描述，研究如下的分数阶非线性Duffing阻尼振动方程：

由于级数解比较复杂这里不再一一列出，其他项可通过Mathematica软件得出，从而方程（25）的近似解可以表示为：

不妨取级数解的前三项并省略高阶项迭代多次得到分数阶阻尼Duffing振动方程的复杂特性如图2，由此可以看出受迫分数阶阻尼振动的运动情况。

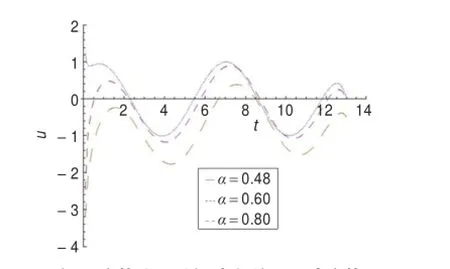
图2 分数阶阻尼振动方程（25）随分数阶导数α的振动情况

图2给出了α=0.48，0.6，0.8三种情况下的图像，可以观察到分数阶振子振动与阻尼项阶数的关系，随着时间的推移呈现衰减的特性。并且α越小，振子的记忆能力越强，振子的变化幅度也就越大。通过引入分数阶的微积分算子来描述黏弹性介质中的阻尼振动往往比人为构造非线性的整数阶方程简单而且更能反应振子运动与阻尼项的关系。

3 结果和讨论

本文利用同伦扰动变换的方法求解了分数阶Duffing振子方程的近似解，并研究了振子振动与分数阶导数之间的关系，为分数阶Duffing振子系统的混沌特性、混沌同步问题等其他特性的研究提供了一定的依据。

[1]王坤，关新平，丁喜峰，等.Duffing振子系统周期解的唯一性与精确周期信号的获取方法[J].物理学报，2010，59（10）：6859-6863.

[2]顾仁财，许勇，郝孟丽，等.Levy稳定噪声激励下的Duffingvan der Pol振子的随机分岔[J].物理学报，2011，60（6）.

[3]刘艳芹.一类分数阶非线性振子的特性研究[J].计算机工程与应用，2012，48（16）：30-32.

[4]Vincent U E，Odunaike R K，Laoye J A，et al.Adaptive backstepping control and synchronization of a modified and chaotic van der Pol-Duffing oscillator[J].Journal of Control Theory and Applications，2011，9（2）：273-277.

[5]Poudlbny I.Fractional differential equations：an introduction to fractional derivatives，fractional differential equations，to methods of their solution and some of their applications[M].New York：Academic Press，1999.

[6]Metzer R，Klafter J.The random walks guide to anomalous diffusion：a fractional dynamics approach[J].Physics Reports，2000，339（1）：1-77.

[7]Ma Junhai，Liu Yanqin.Exact solutions for a generalized nonlinear fractional Fokker-Planck equation[J].Nonlinear Analysis：Real World Applications，2010，11（1）：515-521.

[8]Liu Yanqin，Ma Junhai.Exact solutions of a generalized multi-fractional nonlinear diffusion equation in radical symmetry[J].Communications in Theoretical Physics，2009，52（5）：857-861.

[9]Wang Shaowei，Xu Mingyu.Axial couette flow of two kinds of fractional viscoelastic fluids in an annulus[J]. Nonlinear Analysis：Real World Applications，2009，10（2）：1087-1096.

[10]Adomian G.A review of the decomposition method in applied mathematics[J].Journal of Mathematical Analysis and Applications，1988，135（2）：501-544.

[11]Wazwaz A M，El_Sayed M.A new modification of the adomian decomposition method for linear and nonlinear operators[J].Applied Mathematics and Computation，2001，122（3）：393-405.

[12]He Jihuan.Variational iteration method—a kind of non

linear analytical technique：some examples[J].International

Journal of Non-Linear Mechanics，1999，34（4）：699-708.

[13]Wazwaz A M.The variational iteration method for analytic treatment for linear and nonlinear ODEs[J].Applied Mathematics and Computation，2009，212（1）：120-134.

[14]Erturk V S，Momani S，Odibat Z.Application of generalized differential transform method to multi-order fractional differential equations[J].Communications in Nonlinear Science and Numerical Simulation，2008，13（8）：1642-1654.

[15]Madani M，Fathizadeh M，Khan Y，et al.On the coupling of the homotopy perturbation method and Laplace transformation[J].Mathematical and Computer Modelling，2011，53（9/10）：1937-1945.

[16]Khan Y，Wu Qiaobiao.Homotopy perturbation transform method for nonlinear equations using He’s polynomials[J]. Computers and Mathematics with Applications，2011，61（8）：1963-1967.

[17]Agadjanov.Numerical solution of Duffing equation by the Laplace decomposition algorithm[J].Applied Mathematics and Computation，2006，177（2）：572-580.

LI Na

School of Mathematical Sciences,Dezhou University,Dezhou,Shandong 253023,China

Caputo fractional operator is introduced in the nonlinear Duffing oscillator equation.Homotopy perturbation transform method which is based on homotopy perturbation method and Laplace transform method is applied to solving the fractional nonlinear Duffing oscillator equation and with Mathematica symbols calculation software,the approximate solutions are investigated.The relationship between oscillator movement and fractional derivative is also studied.

Caputo fractional derivative;nonlinear Duffing oscillator equation;homotopy perturbation transform method; approximate solution

将Caputo分数阶微分算子引入到非线性的Duffing振子方程中，运用同伦扰动变换法——一种同伦扰动法和Laplace变换相结合的方法来求解分数阶的非线性方程，借助Mathematica软件的符号计算功能得到了分数阶非线性Duffing振子方程的近似解，研究了振子运动过程与分数阶导数之间的关系。

Caputo分数阶微分；非线性Duffing振子方程；同伦扰动变换法；近似解

A

O175.29

10.3778/j.issn.1002-8331.1304-0070

LI Na.Properties of fractional nonlinear Duffing oscillator equation.Computer Engineering and Applications,2014, 50（18）：75-78.

山东省自然科学基金（No.ZR2010Al019）。

李娜（1979—），女，讲师，主要研究领域为非线性偏微分方程。E-mail：wshlina@163.com

2013-04-07

2013-05-27

1002-8331（2014）18-0075-04

CNKI网络优先出版：2013-06-26，http://www.cnki.net/kcms/detail/11.2127.TP.20130626.1539.015.html