关于定积分的一个性质及其加权推广
时统业, 吴 涵, 韦晓萍
(海军指挥学院 信息系, 南京 211800)
关于定积分的一个性质及其加权推广
时统业, 吴 涵, 韦晓萍
(海军指挥学院 信息系, 南京 211800)
通过建立与高阶可微函数有关的恒等式, 证明了有关文献给出的关于定积分的一个上界, 并给出误差估计,最后给出对带有权函数的定积分的一个上界.
定积分; 可微函数; 上界; 误差估计; 权函数
引言
定理A[1]设函数f:[a, b]→R有2n( n≥2)阶连续导数, 且f(2n)(x)≥0. 令

则有

设函数f在[a, b]上有任意阶导数, 且存在常数M>0, 使得|f(2n)(x)|≤M对任意n∈Z+和任意x∈[a, b]都成立, 则有

本文的目的是通过建立关于2n阶或2n−1阶可微函数的一个积分恒等式, 给出定理A的一个不同的证明.然后分别在的情况下, 给出不等式(1)的误差估计, 最后给出不等式(1)的带有两个独立参数的加权推广.
为方便起见, 记

引理1设f:[a, b]→R有2n( n≥2)阶连续导数, 则有

其中

证明记

简单计算可得


由分部积分法, 得

式(3)、(4)相加即得式(2).
引理2设函数f:[a, b]→R有2n( n≥2)阶连续导数, 则有

其中

证明容易看出p1′(x)=−k1( x),p′2(x)=−k2(x ). 由分部积分法, 得
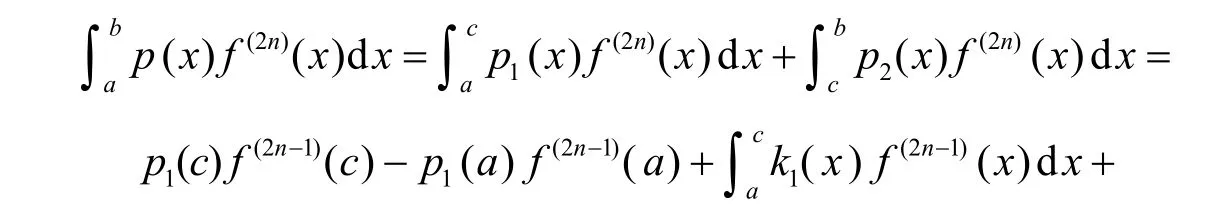

由引理1的式(2), 即可得到式(5).
引理3设函数f:[a, b]→R有2n( n≥2)阶连续导数, 令

则有

其中

证明简单计算可得

由分部积分法, 得

式(7)、(8)相加即得式(6).
主要结果
定理1设函数f:[a, b]→R有2n阶(n≥2)连续导数, 若f(2n)≥0, 则式(1)成立.
证明利用引理1并注意到k( x)在[a, c]∪(c, b]上关于x=c对称, 得
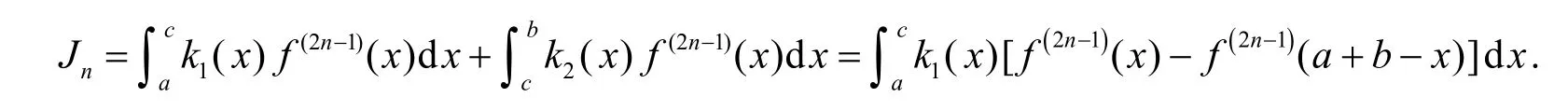
因为f(2n)≥0, 故f(2n−1)在[a, c]上单调不减, 于是当x∈[a, c]时有f(2n−1)(x)−f(2n−1)(a+b−x )≤0. 又因k1( x)≤0, 故有Jn≥0, 即式(1)成立.
定理2设函数f:[a, b]→R有2n( n≥2)阶连续导数, 则有

证明由引理1, 有
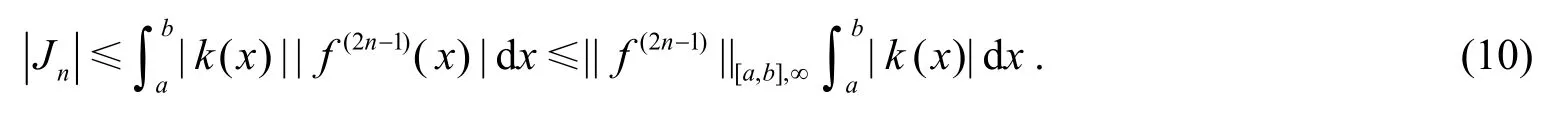
利用|k( x)|在[a, b]上关于x=c对称及k2(x)≥0, 得

由式(10)、(11)可得到式(9)的第一个不等式.由引理2类似可证式(9)的第三个不等式.
由引理1, 得
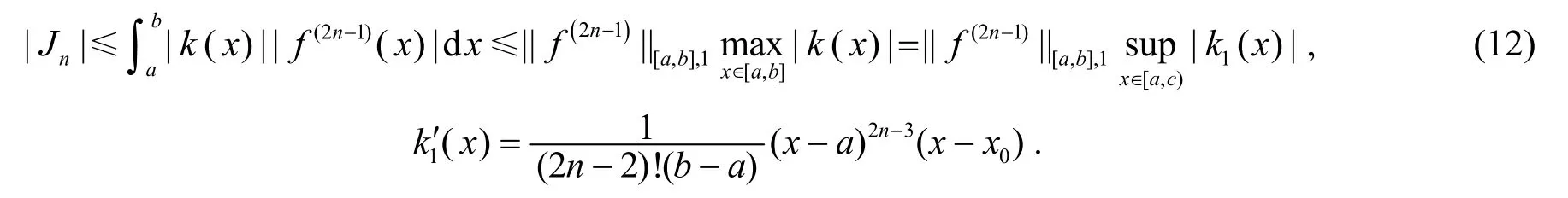
当x∈(a, x0)时, k1′(x)<0; 当x∈(x0, c)时, k1′( x)>0, 故k1( x)在x=x0取最小值. 又k1(x)≤0, 故

由式(12)、(13)得式(9)的第二个不等式.由引理2类似可证式(9)的第四个不等式.
由引理2和Hölder不等式, 得
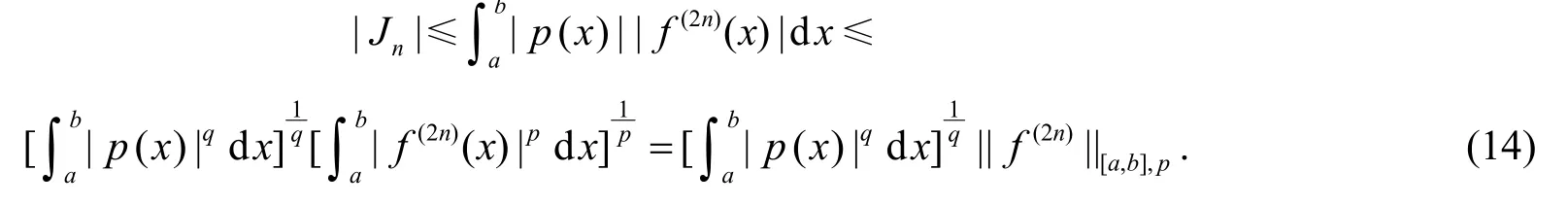
利用|p( x)|在[a, b]上关于x=c对称及p1( x)≥0, 得


由式(14)、(15)、(16)得式(9)的第五个不等式.
定理3设函数f:[a, b]→R有2n( n≥2)阶连续导数, g:[a, b]→R是正的可积函数, 且

若f(2n)≥0, 且是常数), 则有

证明式(17)即Kn≥0. 由引理3, 有

因f(2n)≥0, 故要证明只需证明(x)≥0即可. 当x∈(a, c)时,可表示为
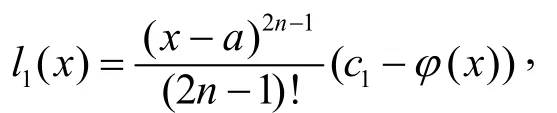

所以ϕ(x)在(a, c)单调增加, 故有ϕ(x)≤ϕ(c)=d1≤c1, 于是有l1( x)≥0. 类似可证l2(x)≥0.
注式(17)可表示为

其中

利用Taylor展开式, 得

其中ξ∈(a, c). 同理有γ2≥0.故式(17)的最好结果是在c1=d1, c2=d2时取得.
推论1设函数f:[a, b]→R有2n( n≥2)阶连续导数, g:[a, b]→R是正的可积函数, 且关于x=c对称, 常数若f(2n)≥0, 则有

由于式(18)中λ的系数非负, 故式(18)的最好结果在λ=d1时取得.特别是当g≡1,时, 得

证明在定理3中取c1=c2=λ即得.
推论2设函数f:[a, b]→R有2n( n≥2)阶连续导数, g:[a, b]→R是正的可积函数. 若f(2n)≥0, 则

特别是当g关于x=c对称时, 有

当n=2时, 由上式得到文[2]的结果:

[1] 文家金, 张日新, 王挽澜.Hermite-Hadamard 不等式的扩张(英文)[J]. 成都大学学报, 2005, 24(4): 241~247
[2] 程海来. Fejér不等式的注记[J]. 大学数学, 2014, 30(1): 38~40
A Property and Its Weighted Generalization About Definite Integral
SHI Tong-ye, WU Han, WEI Xiao-ping
(Department of Information, PLA Naval Command College, Nanjing 211800, China)
Some integral identities involving higher order differentiable functions are established. A new proof of an upper bound on definite integral is given by the identity. Error estimations and an upper bound on definite integral with weighted function also are given.
definite integral; differentiable function; upper bound; error estimation; weighted function
O178; O172
A
: 1672-5298(2014)04-0001-05
2014-08-20
时统业(1963−), 男, 河北张家口人, 硕士, 海军指挥学院信息系副教授. 主要研究方向: 基础数学

