基于自适应高频谐波LMD法的风电机组故障诊断

武英杰， 刘长良， 范德功

(1． 华北电力大学 控制与计算机工程学院， 北京 102206； 2． 华北电力大学 新能源电力系统国家重点实验室， 北京 102206； 3． 北京金风科创风电设备有限公司， 北京 100176)

基于自适应高频谐波LMD法的风电机组故障诊断

武英杰1， 刘长良2， 范德功3

(1． 华北电力大学 控制与计算机工程学院， 北京 102206； 2． 华北电力大学 新能源电力系统国家重点实验室， 北京 102206； 3． 北京金风科创风电设备有限公司， 北京 100176)

针对实际应用中局部均值分解(LMD)法存在的模态混叠问题，提出了自适应高频谐波LMD法.分析了信号中异常事件对求取包络函数和均值函数的影响，将构造的自适应高频谐波加入到原始信号中，通过改变原始信号的极值点位置来抑制模态混叠现象.对含有典型异常事件的信号进行了自适应高频谐波LMD法和ELMD法仿真实验对比，验证了该算法的有效性和优越性.将该算法应用于风电机组传动系统故障诊断中，结果表明：采用该算法后，原有的模态混叠状况得到明显改善，并成功提取出轴系不平衡故障特征，可为风电机组故障诊断提供参考.

局部均值分解； 模态混叠； 自适应高频谐波； 风电机组； 故障诊断

我国风电机组装机总量位居世界第一，随着装机容量的增加，机组逐步进入故障高发期.传动系统作为机组的关键部分，故障率较高[1]，常见故障有轴承磨损、轴系不平衡和不对中以及齿轮损伤等.风电机组振动信号具有调幅-调频特性，并且风电机组处于特殊的工作环境，信号中不可避免地混有噪声和随机干扰脉冲，因此传统的故障诊断算法具有一定局限性[2].

由于风电机组振动信号具有非平稳性和非线性，因此采用时频分析方法更为合理.局部均值分解(LMD)法是一种新的时频分析方法[3]，该方法能够将振动信号自适应地分解为多个PF(product function)分量和残余量之和的形式，其中每个PF分量由一个包络信号和一个纯调频信号的乘积构成，PF分量的瞬时频率可直接根据纯调频信号求取，分量包络谱可由包络信号得到.另外，LMD法能有效提取风电机组传动系统的故障特征，且比常见的时频分析方法具有更好的自适应性，因此，LMD法在旋转机械故障诊断中引起了广泛关注[4-5].

LMD法虽然比经验模态分解(EMD)法更为温和[3]，但同样存在模态混叠和端点效应问题[6-8].模态混叠现象源于Huang对间歇信号的EMD法分解[9].赵进平[10]把由间歇信号、干扰脉冲和随机噪声等引起模态混叠的不连贯信号的事件统称为异常事件.实际振动信号中，异常事件无法避免，很可能导致LMD法无法分解出具有物理意义的PF分量.

抑制模态混叠的方法大致可分为3类：滤波法、异常排除法和加入信号法.滤波法通过小波分解对原始信号进行重构[11-12]，旨在过滤掉异常事件，但该方法存在小波(基)选择和阈值设定的问题，而且不能将异常事件完全过滤.异常排除法[9-10,13]事先寻找异常点特征，并将其排除或分离，此类方法对异常信号有一定要求，缺乏普适性.加入信号法通过加入具有某种特征的信号，改变原始信号中极值点的分布，从而达到抑制模态混叠的目的，该方法简单、有效，已在EMD法中得到广泛应用[14-16].

Yang等[6]将白噪声信号引入到LMD法中，即集总局部均值分解(ELMD)法，模态混叠现象得到明显抑制，但LMD法本身已为3层循环，ELMD法将使计算量进一步增大，另外白噪声信号的添加幅度和平均次数对ELMD法的分解也有影响.

笔者借鉴EMD法抑制模态混叠的方法，提出自适应高频谐波LMD法，通过仿真实验证明其有效性，并将其应用于风电机组故障诊断中.

1 LMD法及模态混叠

1.1 LMD法概述

LMD法由3层循环构成，最里层通过滑动平均求取信号的局部包络函数和局部均值函数；中间层求取纯调频信号和包络信号，并得到单个PF分量；最外层为LMD法停止的判断条件.算法概述如下：

(1) 求取局部包络函数和局部均值函数.

首先确定信号的所有极值点，计算2个连续极值间的局部均值和局部包络值，折线连接所有相邻的均值点和包络点，再利用滑动平均对其进行平滑处理，进而求得局部均值函数和局部包络函数.

(2) 求取纯调频信号和包络信号.

理想情况下，原始信号减去求得的局部均值函数并进行解调处理，可得到纯调频信号，其局部包络函数为1；否则，将解调后的信号作为原始信号重复以上迭代过程，直至求得纯调频信号.将迭代过程中产生的局部包络函数相乘得到第一个PF分量的包络信号.

(3) 求取PF分量.

将所得的纯调频信号与包络信号相乘得到第一个PF分量，将其从原始信号中分离后，重复以上步骤k次，直至残余量为单调函数.最终，原始信号被分解为k个具有明显物理意义的PF分量与残余量之和.

1.2 模态混叠

模态混叠是指在一个PF分量中包含差异极大的特征时间尺度，或者相近的特征时间尺度分布在不同的PF分量中.由于LMD法和EMD法类似，均为基于极值点的包络信号求取方式，需经过多次筛选得到不同特征尺度的各级分量，因此，标准的LMD法算法同样存在模态混叠和端点效应问题.

笔者选用文献[7]中异常事件的仿真信号进行分析，其中x(t)包含周期性衰减脉冲信号.

x(t)=1.2sin(20πt)+ 0.5exp(-80t)sin(240πt)

(1)

图1所示为LMD法模态混叠曲线.由曲线gs可知，异常事件改变了信号的真实包络值和真实均值，其中，曲线1和曲线2分别为求取第一个纯调频信号时的局部包络函数和局部均值函数，与真实的直线包络函数和直线均值函数相比，两者已产生严重变形，尤其是局部包络函数.由于第1个PF分量PF1的包络信号是多个局部包络函数的乘积，因此，迭代次数越多，包络信号的误差就越大.如图1所示，PF1中包含了第2个PF分量PF2的成分，出现明显的模态混叠现象.

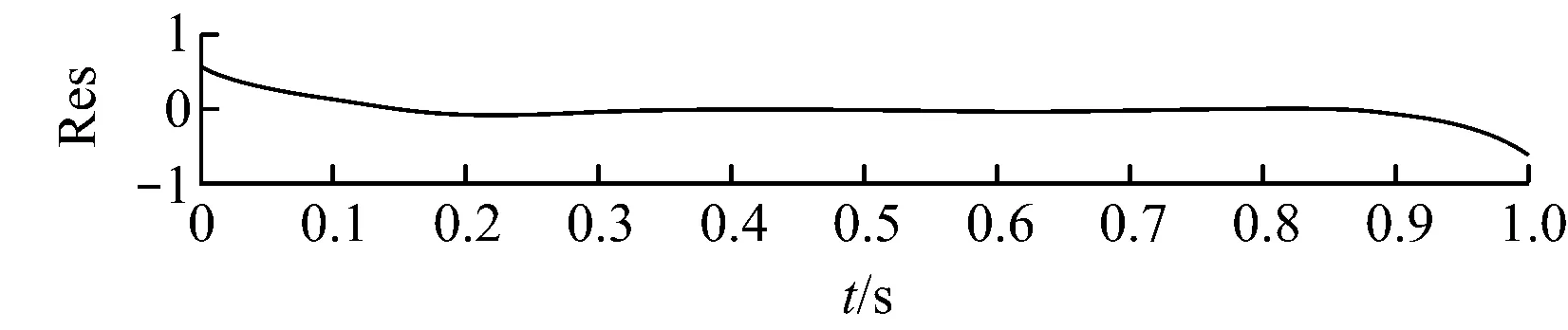
图1 LMD法模态混叠曲线

另外，笔者对含有干扰脉冲和随机噪声的信号进行LMD法分解，发现同样存在模态混叠现象，由于篇幅限制，不一一列出.

2 自适应高频谐波LMD法及仿真实验

2.1 自适应高频谐波LMD法

胡爱军等[16]提出将高频谐波引入到EMD法中，其中高频谐波频率可根据采样频率，在分析频率的上限附近选择，高频谐波幅值一般接近原始信号的峰值.引入的结果显示，异常事件被淹没在高频谐波中，模态混叠现象得到有效抑制，但此方法需要手动确定高频谐波的频率和幅值.

笔者根据包络信号和纯调频信号的物理意义，构造了具有自适应性的高频谐波，并将其一次性加入到原始信号中，通过改变原始信号的极值点位置以淹没或分离出异常事件，从而达到抑制模态混叠的目的.

为避免端点效应对实验结果的影响，本算法采用特征波延拓的方法进行端点处理[8, 17]，分解过程中纯调频信号的认定条件以及LMD法的终止条件依然根据延拓前的数据进行判断.自适应高频谐波LMD法流程图如图2所示.

(1) 对原始信号进行单次LMD法分解，即仅求取PF1的纯调频信号s1n(t)和包络信号a1(t)：

s1n(t)=cos ϑ1(t)

(2)

a1(t)=a11(t)a12(t)…a1n(t)

(3)

式中：ϑ1(t)为纯调频信号相位函数；a1n(t)为第n次迭代中的包络函数，极限值为1.

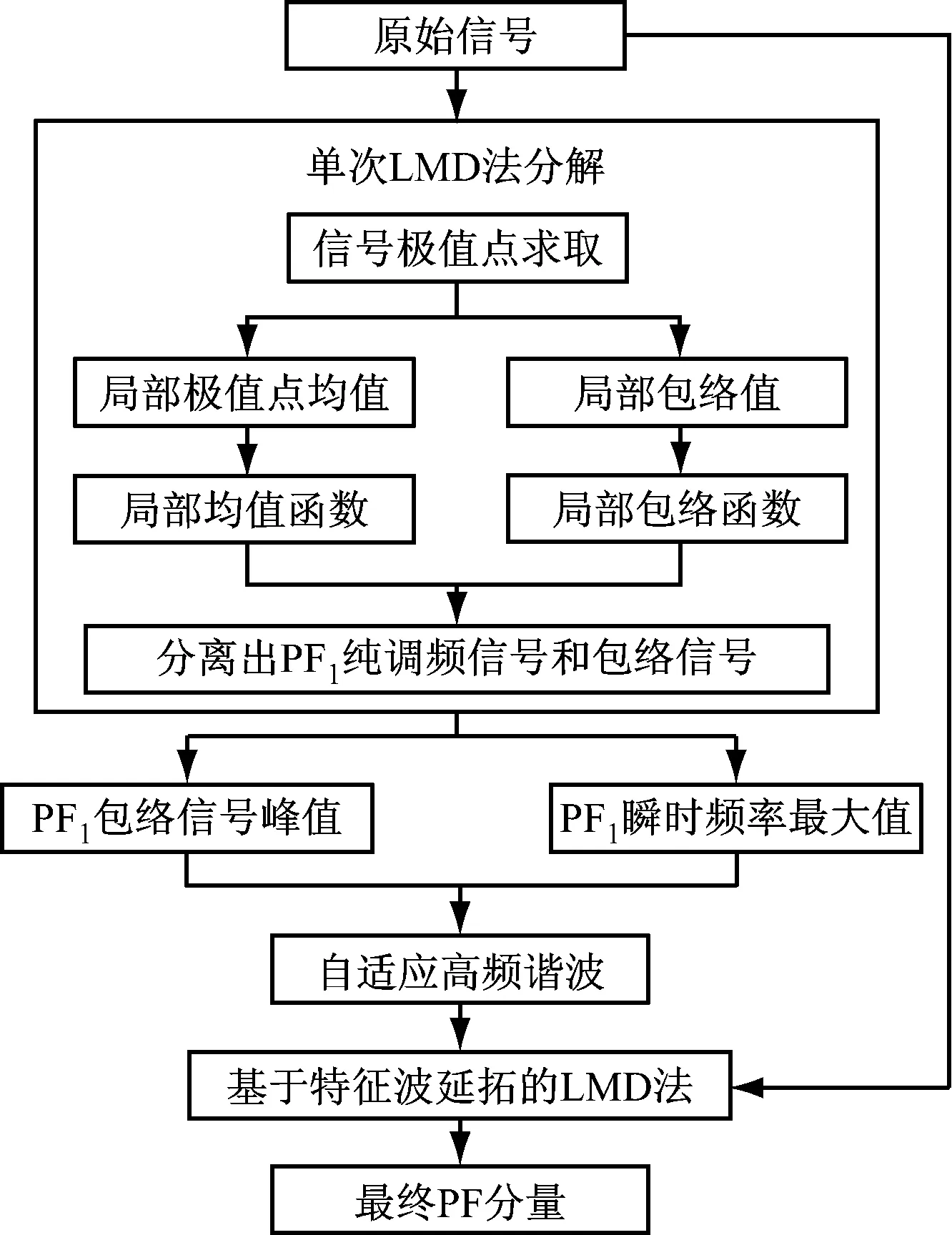
图2 自适应高频谐波LMD法流程图

(2) 构造自适应高频谐波函数X(t).

计算PF1分量的瞬时频率ω1(t)

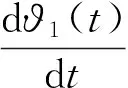
(4)

ϑ1(t)=arccos(s1n(t))

笔者借鉴文献[16]中的构造思路，选择单次LMD法分解中PF1瞬时频率的最大值作为自适应高频谐波的频率，选择PF1包络信号的峰值作为自适应高频谐波的幅值，可得：

X(t)=mean(a1(t))× sin2max(ω1(t))×2πt

(5)

(3) 将自适应高频谐波和原始信号叠加后，再进行经特征波延拓的LMD法分解，并得到最终的PF分量.

2.2 仿真实验

采用自适应高频谐波LMD法对含有周期性衰减脉冲的信号进行分解(由于高频谐波频率取值为PF1瞬时频率最大值的单倍值，因此称之为单倍最高频率法)，所得结果如图3所示.其中gx-s为加入自适应高频谐波并经过特征波延拓的波形，PF1中异常事件被高频谐波淹没，PF2为原始信号中的正弦分量，因此，单倍最高频率法能够根据信号自身特点，自动构造高频谐波函数，有效抑制异常事件引起的模态混叠.

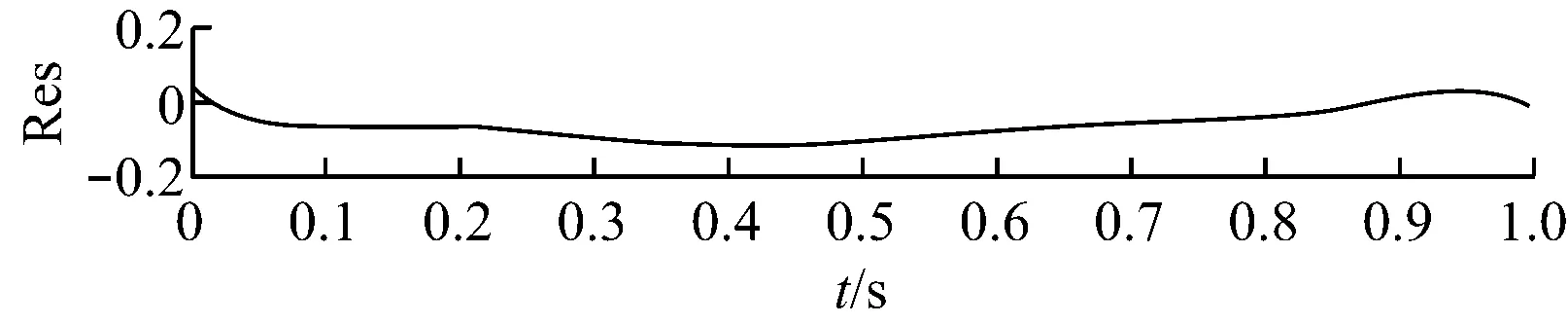
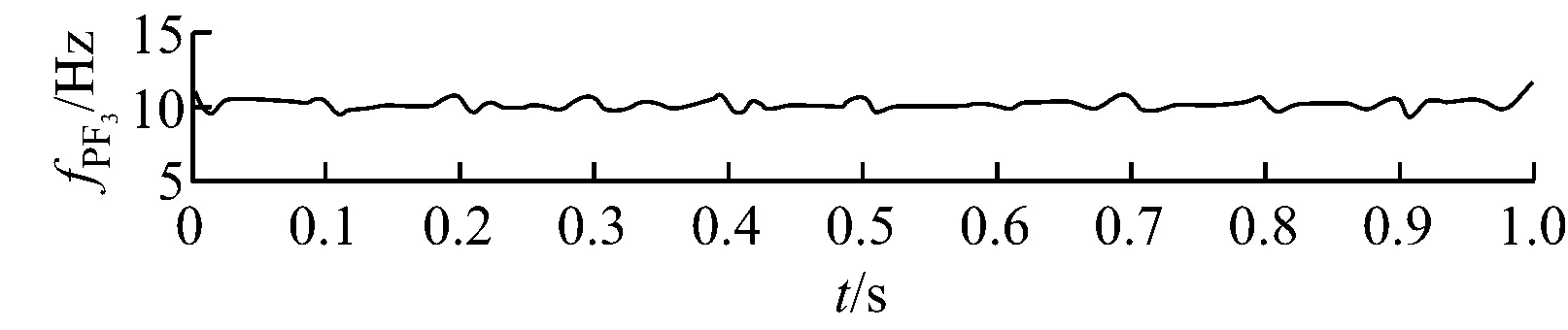
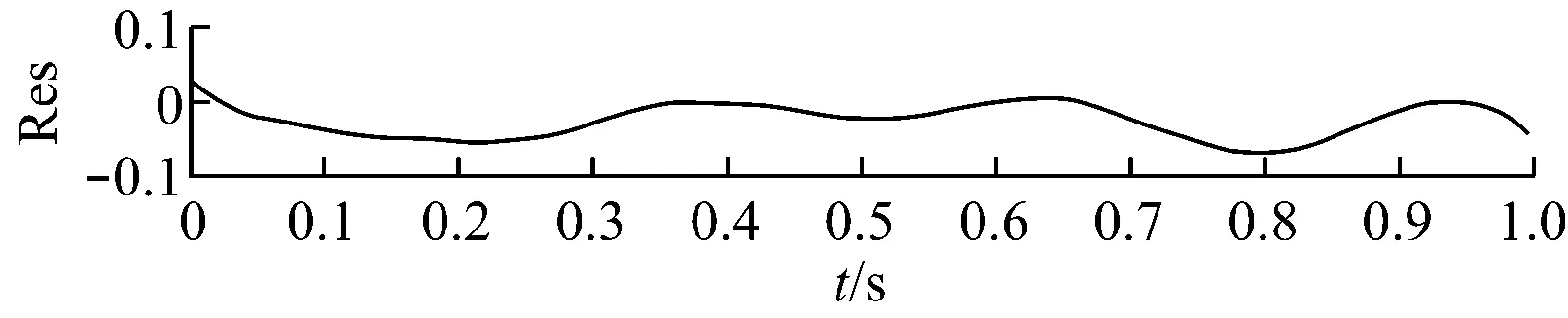
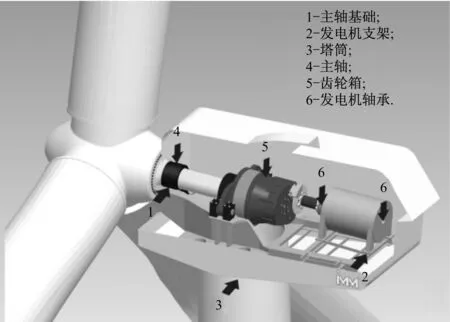
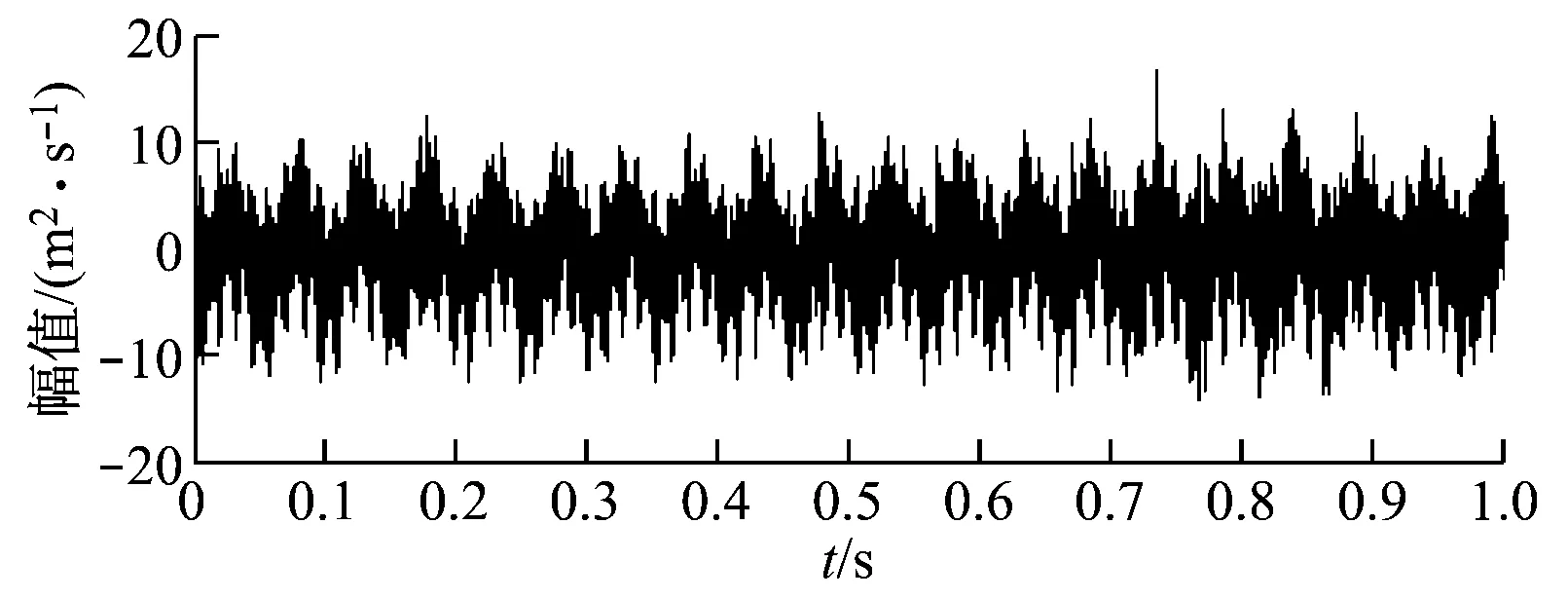
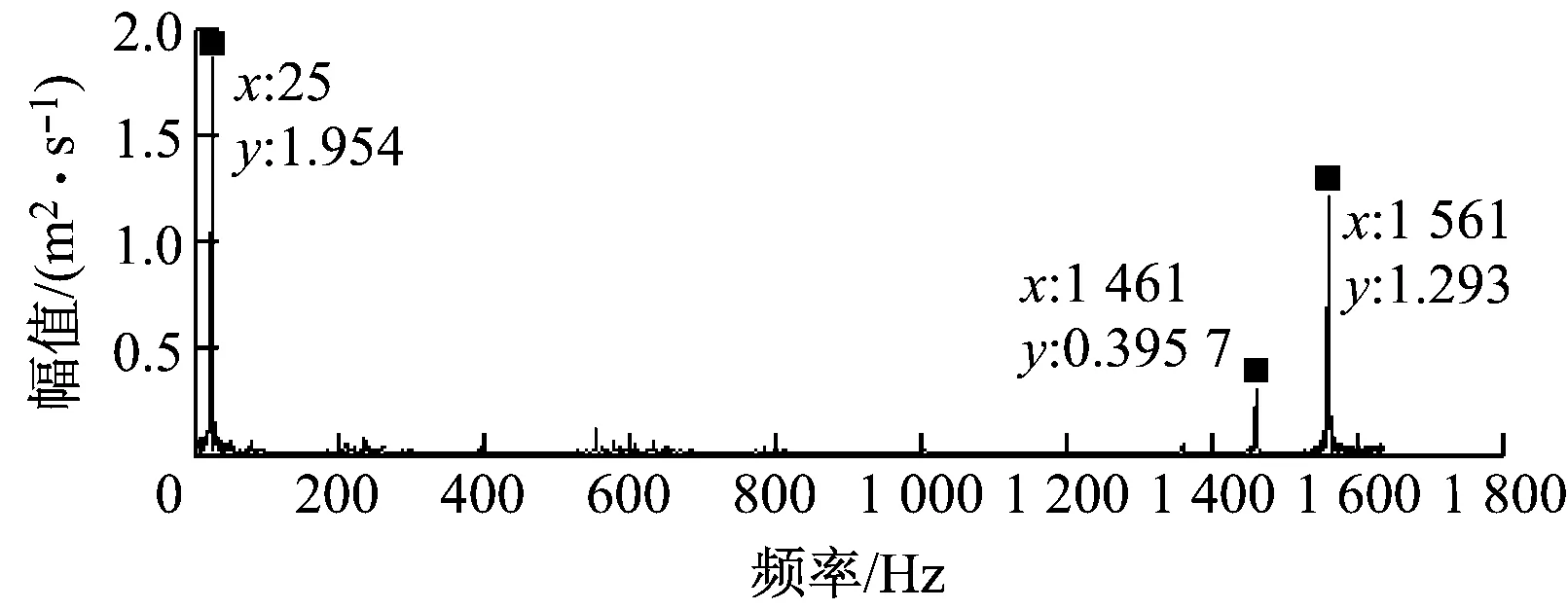
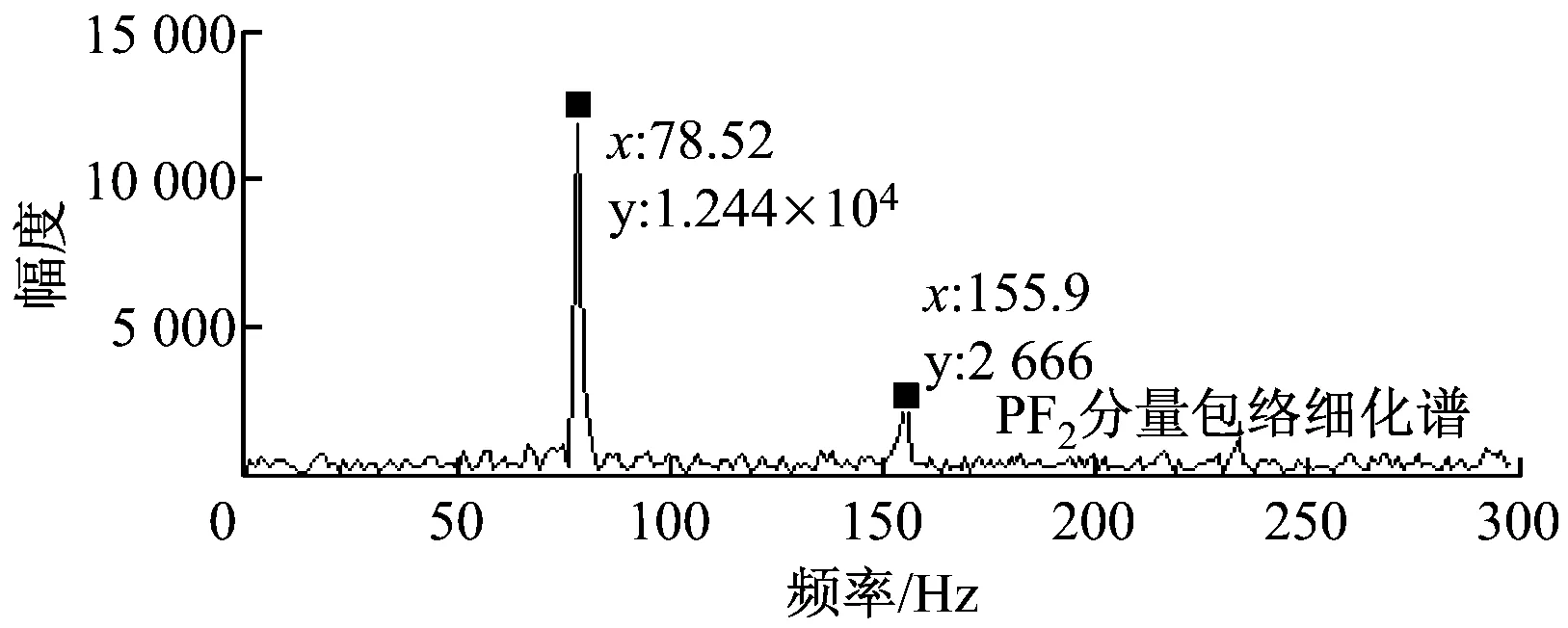
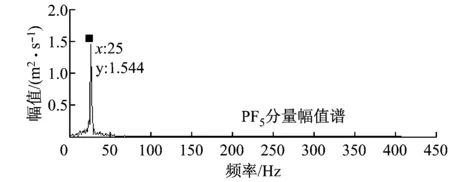
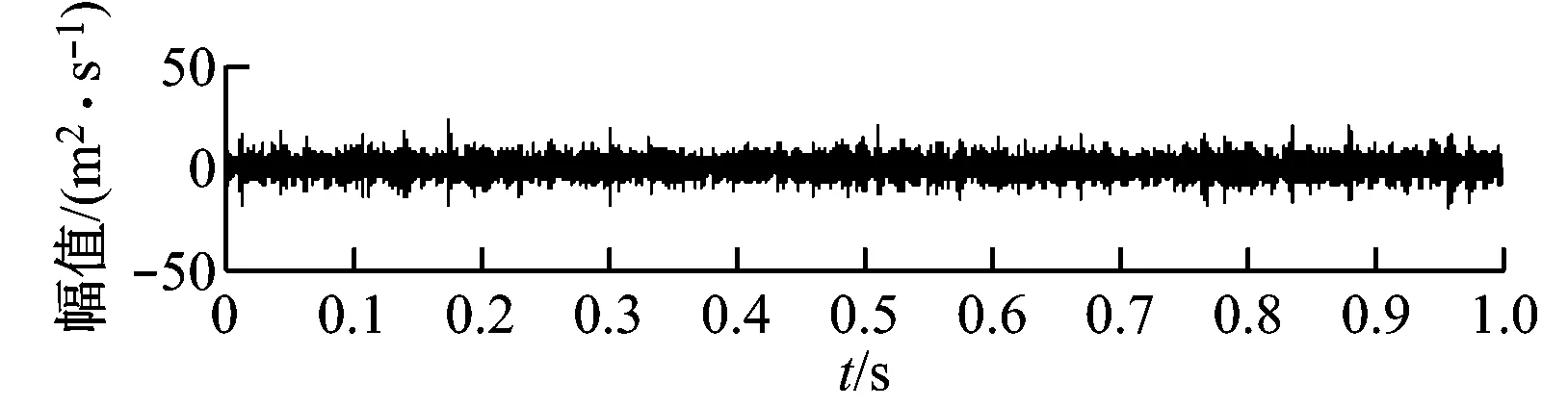
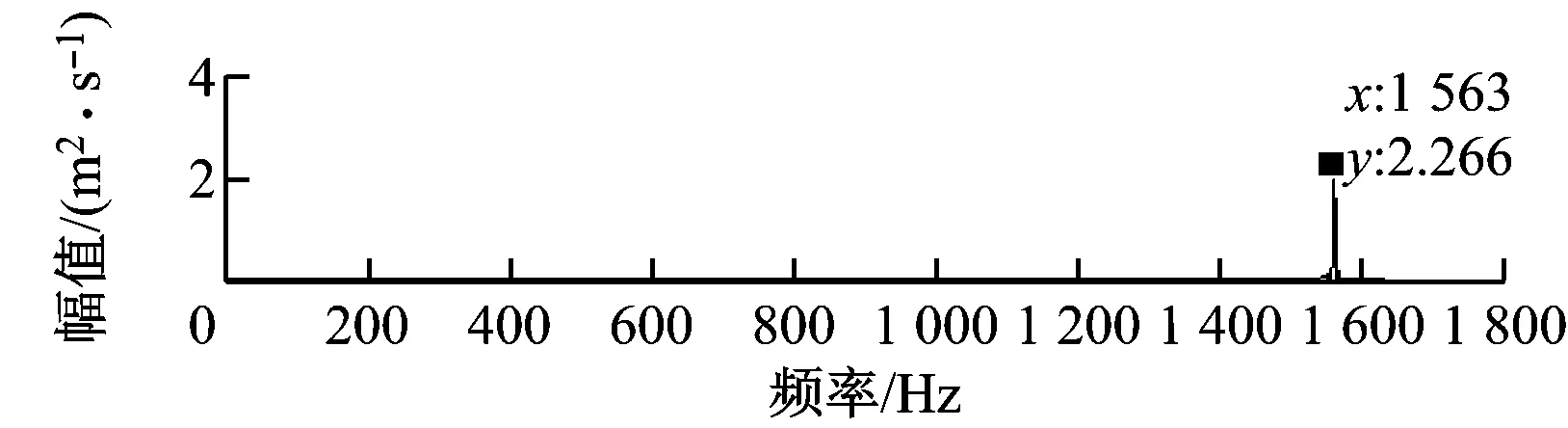
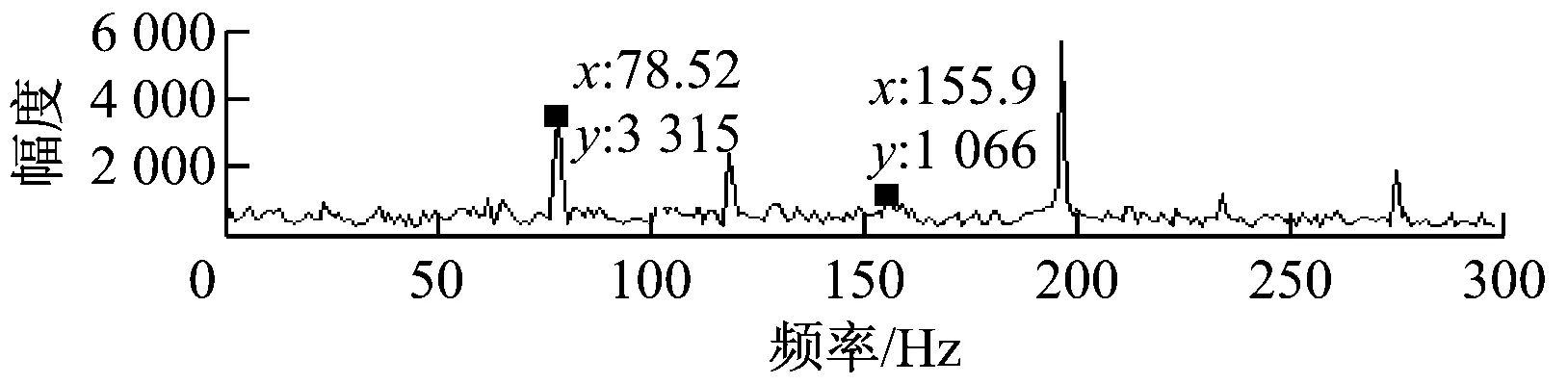
单倍最高频率法可将异常事件淹没在高频谐波中，但未能将其分离.文献[18]中指出，在EMD法中，当2个正弦分量满足0.5

图3 基于单倍最高频率法的LMD法分解结果

选择单次LMD法分解中PF1瞬时频率最大值的2倍作为自适应高频谐波的频率，幅值仍选择包络信号的峰值(下文简称为双倍最高频率法)，再次进行仿真实验，分解效果如图4(a)所示，其中PF1为构造的自适应高频谐波，PF2为分离出的异常事件，PF3为原始信号中的正弦分量.

图4(b)为各分量的瞬时频率，PF1的瞬时频率在335 Hz附近，对应自适应高频谐波的频率；PF2的瞬时频率呈现以10为周期的波动，对应周期性衰减脉冲频率；PF3的瞬时频率稳定在10 Hz附近.

为验证本算法的优越性，采用ELMD法对相同信号进行仿真分析.ELMD法采用白噪声信号,具有均匀地“污染”目标信号整个时频空间的性质，在LMD法分解前加入幅值不同的白噪声信号，不同尺度的分量将自动分解到白噪声所确定的滤波器组中，从而减轻模态混叠现象[6].

据标准EEMD程序对内禀模函数(IMF)个数的限制方法，将PF分量个数固定为：log2(xsize)-n，其中xsize=1 200，为前后各延拓100个点之后的数据，n可根据分解需要手动调整.ELMD法分解中，加入标准差为0.02的白噪声信号，平均100次，分解结果如图5所示.由图5可知，周期性衰减脉冲PF1被成功提取出来，但PF3中仍包含PF2的成分.通过对比可知，文献[7]中虽然分解出2个PF分量，但残余量中同样包含着第2个分量的特征尺度.另外，采用特征波延拓的ELMD法时端点效应要小一些.

(a) 各PF分量

(b) PF分量的瞬时频率

图5 ELMD法分解结果

3 风电机组传动系统故障诊断

主流风电机组传动系统包括主轴、齿轮箱、发电机和联轴器等，其主要部件可分为轴系、滚动轴承和各级齿轮.选取某750 kW风电机组传动系统现场振动数据进行分析，参考VDI 3834标准进行数据采集，其测点分布示意图如图6所示[19]，其中每个测点都装有水平、垂直和轴向3组传感器.

图6 测点示意图

通过与其他同类型风电机组对比发现，该风电机组发电机前端振动数据表现异常，取测点6垂直方向的加速度数据进行分析，其中，采样频率为12 800 Hz，发电机转速为1 519.7 r/min.表1为发电机轴承故障特征频率.

表1 发电机轴承故障特征频率

选取发电机前端轴承1 s内的振动数据进行分析，结果如图7所示.由图7可知，振动信号具有明显的调幅特性，表现为整体周期性波动，并包含冲击脉冲和随机噪声.首先，对故障信号进行频谱分析，其中25 Hz接近发电机转动频率25.3 Hz，但在1 461 Hz和1 561 Hz处也出现明显峰值，因此，仅根据频谱分析无法作出准确的判断.

(a) 原始信号

(b) 频谱分析图

采用标准LMD法对振动信号进行分解，结果如图8(a)所示.由图8(a)可知，PF2具有明显的冲击特性，PF5分量包含周期性波动，但出现了明显的模态混叠现象，部分分量留在了残余量中，对故障的准确定位产生影响.

采用ELMD法对振动信号进行分解，结果如图8(b)所示.由图8(b)可知，信号中的周期性波动成分被分离出来，PF5分量的模态混叠现象得到抑制，但PF6分量中仍包含同样的特征尺度，与ELMD法仿真实验结论一致.

最后，采用笔者提出的自适应高频谐波LMD法对振动信号进行分解，结果如图8(c)所示.由图8(c)可知，原始信号中的冲击成分和周期性波动都被成功分离出.通过对比分析可知，本算法残余量明显小于LMD法，PF分量较ELMD法更加精简，在消除模态混叠的同时没有增加虚假PF分量，有助于故障的进一步判断.

LMD法分解中，冲击分量和周期性波动分量是分析的重点.对PF2分量的包络信号进行细化谱分析，结果如图8(d)所示.由图8(d)可知，78.52 Hz与发电机轴承外圈故障特征频率79.21 Hz相差0.69 Hz；对PF5分量进行频谱分析可知，25 Hz与发电机转动频率25.3 Hz相差0.3 Hz.

由于故障特征频率偏差较大，尚不足以对故障进行定位，笔者对其他正常运行、同转速、同类型及同测点的机组振动数据进行上述分析，发现频谱中没有出现25 Hz，但78.52 Hz及其二倍频仍然存在，只是幅度偏小，如图9所示，因此可排除78.52 Hz作为故障特征频率的可能性.

(a) LMD法分解结果

(b) ELMD法分解结果

(c) 自适应高频谐波LMD法分解结果

(d) PF2包络细化谱与PF5幅值谱

(a) 同类型机组同测点振动数据

(b) 信号FFT

(c) PF2分量包络细化谱

由于实际故障特征频率与计算值之间存在误差，因此可认为25 Hz为发电机转动频率，结合自适应高频谐波LMD法的分解结果，推测机组齿轮箱高速轴和发电机驱动端之间存在不平衡故障，后经维护人员平衡处理，发电机驱动端不平衡故障消失.

4 结 论

(1) 笔者提出的自适应高频谐波LMD法可将异常事件淹没或分离，成功抑制模态混叠现象.

(2) 自适应高频谐波LMD法和ELMD法对抑制异常事件引起的模态混叠现象均有效，但前者计算过程简单，计算结果不增加虚假PF分量，且具有自适应性.

(3) 现场数据分析表明，自适应高频谐波LMD法能有效消除信号中干扰脉冲和随机噪声引起的模态混叠现象，并成功排除和提取出故障特征，为风电机组传动系统故障诊断提供参考.

[1] 陈雪峰，李继猛，程航，等.风力发电机状态监测和故障诊断技术的研究与进展[J].机械工程学报，2011，47(9)：45-52.

CHEN Xuefeng, LI Jimeng, CHENG Hang,etal. Research and application of condition monitoring and fault diagnosis technology in wind turbines[J].Journal of Mechanical Engineering, 2011, 47(9): 45-52.

[2] 胡劲松，杨世锡.基于HHT的旋转机械故障诊断方法研究[J]. 动力工程，2004，24(6)：845-851.

HU Jinsong, YANG Shixi. Research on HHT-based fault diagnosis method for rotating machinery[J]. Power Engineering, 2004, 24(6):845-851.

[3] SMITH J S. The local mean decomposition and its application to EEG perception data[J]. Journal of the Royal Society Interface, 2005, 2(5):443-454.

[4] LIU W Y, ZHANG W H, HAN J G,etal. A new wind turbine fault diagnosis method based on the local mean decomposition[J].Renewable Energy, 2012, 48:411-415.

[5] FENG Zhipeng, ZUO Ming J, QU Jian,etal. Joint amplitude and frequency demodulation analysis based on local mean decomposition for fault diagnosis of planetary gearboxes[J].Mechanical Systems and Signal Processing, 2013，40(1):56-75.

[6] YANG Yu, CHENG Junsheng, ZHANG Kang. An ensemble local means decomposition method and its application to local rub-impact fault diagnosis of the rotor systems[J]. Measurement, 2012，45 (3):561-570.

[7] 廖星智，万舟，熊新.基于ELMD与LS-SVM的滚动轴承故障诊断方法[J]. 化工学报,2013,64(12):4667-4673.

LIAO Xingzhi, WAN Zhou, XIONG Xin. Fault diagnosis method of rolling bearing based on ensemble local mean decomposition and least squares support vector machine[J]. CIESC Journal, 2013,64(12):4667-4673.

[8] 张亢，程军圣，杨宇. 基于自适应波形匹配延拓的局部均值分解端点效应处理方法[J].中国机械工程，2010，21(4)：457-462.

ZHANG Kang,CHENG Junsheng,YANG Yu. Processing method for end effects of local mean decomposition based on self-adaptive waveform matching extending. [J]. China Mechanical Engineering, 2010,21(4):457-462.

[9] HUANG N E, SHEN Z, LONG S R. A new view of nonlinear water waves: the Hilbert spectrum [J]. Annual Review of Fluid Mechanics, 1999, 31:417-457.

[10] 赵进平.异常事件对EMD方法的影响及其解决方法研究[J]. 青岛海洋大学学报,2001,31(6):805-814.

ZHAO Jinping. Study on the effects of abnormal events to empirical mode decomposition method and the removal method for abnormal signal[J]. Journal of Ocean University of Qingdao, 2001,31(6):805-814.

[11] LIU Yibing, WU Qi, MA Zhiyong,etal. An improved Hilbert-Huang transform and its application in faults signal analysis[C]//Proceedings of the 2006 IEEE International Conference on Mechatronics and Automation. Luoyang, China: IEEE Press, 2006.

[12] PENG Z K, TSE P W, CHU F L. An improved Hilbert-Huang transform and its application in vibration signal analysis [J]. Journal of Sound and Vibration, 2005，286 (1/2):187-205.

[13] 胡重庆，李艾华. EMD间歇信号的检测和提取方法[J]. 数据采集与处理, 2008, 23(1):108-111.

HU Chongqing, LI Aihua. Method for detecting and extracting intemittency signal in EMD[J]. Journal of Data Acquisition & Processing, 2008, 23(1):108-111.

[14] DEERING R, KAISER J F. The use of a masking signal to improve empirical mode decomposition[C]//International Conference on Acoustics, Speech, and Signal Processing，2005. Philadelphia, PA, USA： IEEE,2005: 485-488.

[15] WU Zhaohua，HUANG N E. Ensemble empirical mode decomposition：a noise-assisted data analysis method[J].Advances in Adaptive Data Analysis, 2009,1(1):1-41.

[16] 胡爱军，孙敬敬，向玲.经验模态分解中的模态混叠问题[J]. 振动、测试与诊断, 2011,31(4):429-434.

HU Aijun, SUN Jingjing, XIANG Ling. Mode mixing in empirical mode decomposition[J]. Journal of Vibration, Measurement & Diagnosis, 2011,31(4):429-434.

[17] 胡爱军，安连锁，唐贵基.HILBERT-HUANG变换端点效应处理新方法[J].机械工程学报，2008，44(4):154-158.

HU Aijun, AN Liansuo, TANG Guiji. New process method for end effects of HILBERT-HUANG transform[J].Chinese Journal of Mechanical Engineering, 2008，44(4):154-158.

[18] RILLING G, FLANDRIN P, GONCALVèS P. On empirical mode decomposition and its algorithms[C]//IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing. Grado, Italy: IEEE, 2003:8-11.

[19] BLATT.VDI 3834 Blatt1/Part1:2009 measurement and evaluation of the mechanical vibration of wind energy turbines and their components-onshore wind energy turbines with gears[S]. Berlin, Germany: Beuth Verlag，2009.

Wind Turbine Fault Diagnosis Based on Adaptive High-frequency Harmonics LMD

WUYingjie1,LIUChangliang2,FANDegong3

(1. School of Control and Computer Engineering, North China Electric Power University, Beijing 102206, China; 2. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Beijing 102206, China; 3. Beijing Goldwind Science & Creation Wind Power Equipment Co., Ltd., Beijing 100176, China)

To solve the mode mixing problem of local mean decomposition (LMD) in actual applications, an adaptive high-frequency harmonics LMD was proposed. The effect of abnormal events on the envelope function and mean function was analyzed, and the adaptive high-frequency harmonics were constructed and added into the signal to deal with the mode mixing problem by changing the distribution of extreme points of the original signal. Simulation comparison was made to signals containing typical abnormal events between adaptive high-frequency harmonics LMD (AHLMD) and ensemble LMD (ELMD), illustrating the effectiveness and superiority of AHLMD, which was subsequently applied to fault diagnosis for the drive train system of a wind turbine. Results show that the mode mixing situation can be improved significantly and the shaft unbalance characteristics can be extracted successfully via the method, which therefore may serve as a reference for fault diagnosis of wind turbines.

LMD; mode mixing; adaptive high-frequency harmonics; wind turbine; fault diagnosis

1674-7607(2014)12-0952-07

TP273

A

510.80

2014-02-20

2014-04-01

中央高校基本科研业务费专项资金资助项目(13MS102)

武英杰(1986-)，男，河北邢台人，博士研究生，研究方向为：风电机组故障诊断.电话(Tel．)：13731293815； E-mail：wuyingjie6668@163.com．