基于分层模态综合法的大型汽轮发电机组转子-末级叶片耦合系统扭转振动分析

徐自力， 窦柏通， 范小平， 方 宇， 王建录， 曹守洪

(1. 西安交通大学 机械结构强度与振动国家重点实验室， 西安 710049；2. 东方汽轮机有限公司， 四川德阳 618000)

基于分层模态综合法的大型汽轮发电机组转子-末级叶片耦合系统扭转振动分析

徐自力1， 窦柏通1， 范小平2， 方 宇2， 王建录2， 曹守洪2

(1. 西安交通大学 机械结构强度与振动国家重点实验室， 西安 710049；2. 东方汽轮机有限公司， 四川德阳 618000)

针对应用三维有限元法计算大型汽轮发电机组转子-末级叶片耦合系统扭转振动时存在自由度多和难以实现等问题，在模态综合法(CMS)的基础上，推导了计算转子-末级叶片耦合系统振动的分层二重CMS法的基本方程，给出了降阶的思路和原理.采用该方法对某1 000 MW汽轮发电机组的转子、末级和次末级叶片组成的耦合系统进行了扭转振动特性计算和分析，与不考虑末级、次末级叶片实际结构影响的固有振动特性进行了对比.结果表明：如果不考虑末级叶片的实际结构，会漏掉一些重要的振动模态，给转子和叶片的安全带来隐患；降阶前系统的自由度达到1.5亿，而降阶后系统的广义自由度仅为原自由度的0.07%；分层二重CMS法可用于大功率机组转子、末级、次末级耦合系统的扭转振动分析.

汽轮发电机组； 转子； 分层二重CMS法； 末级叶片； 扭转振动

转子-末级叶片系统是汽轮发电机组的核心部件，其扭转振动特性直接影响机组的安全运行[1].以往对转子和叶片的设计往往忽略两者的耦合作用[2]，但随着长叶片的使用，转子的扭转振动与轮盘-叶片系统的切向振动，特别是与末级成圈叶片的零节径伞形振动的耦合作用越来越强[2-3]，因耦合扭转振动而导致汽轮发电机组损坏的事故时有发生[4-5].因此，准确掌握转子-末级叶片耦合系统的扭转振动特性是机组设计和运行中需关注的重要问题之一.

郭力等[6]将转子作为主部件，末级叶片系统作为分支部件，并将分支部件的各阶模态简化为等效的质量-弹簧系统，通过分析简化系统的振动可知，末级叶片零节径振动频率与轴系的扭转振动频率接近时会发生耦合扭转振动.Okabe等[2,7]应用类似于模态综合法的准模态技术，将非耦合末级叶片系统的伞形振动模态简化为一个等效的质量-弹簧系统，根据测得的实际转子的模态参数修正转子-叶片等效缩减模型，并对700 MW汽轮发电机组的轴系耦合系统扭转振动频率进行估算，估算值与现场验证结果吻合较好.鲍文等[8]采用分布参数模型对300 MW汽轮机轴系-叶片耦合系统进行了等效模拟，计算了系统扭转振动特性，发现末级叶片A0型振动与轴系会产生耦合振动，该耦合振动会降低叶片振动频率的避开率.杨建刚等[9]应用改进阻抗匹配方法分析轴系-叶片耦合系统动力特性，发现在某些情况下叶片对轴系扭转刚度的影响大于对转动惯量的影响.尽管已有学者对汽轮发电机组转子和末级叶片耦合扭转振动进行了研究，揭示成圈叶片与转子扭转振动之间的耦合作用，但其大多对末级叶片系统进行了等效处理，没有真实地反映末级叶片系统实际结构的影响.

为准确计算转子扭转振动和末级、次末级叶片系统切向振动的耦合作用，推导了分层二重模态综合法(CMS)计算转子-末级叶片系统耦合振动的基本方程，给出了降阶的思路和原理.采用该方法，并应用三维六面体二次单元对某1 000 MW汽轮机转子-末级叶片耦合系统的扭转振动特性进行了计算，且与未考虑末级、次末级叶片实际结构影响的振动特性进行了对比.

1 分层二重CMS法的基本原理

大型汽轮发电机组转子-末级叶片系统结构复杂、尺寸大，如1 000 MW等级机组轴向长度达到50 m.在采用三维有限元法计算其扭转振动特性时，自由度达到数千万，甚至超过亿.即使采用固定界面CMS法仍会超过计算机的容量，难以完成转子系统振动的数值模拟.因此，还需要在固定界面CMS法的基础上对自由度做进一步缩减.笔者给出了计算大型汽轮发电机组转子-末级叶片系统扭转振动特性的分层二重CMS法.

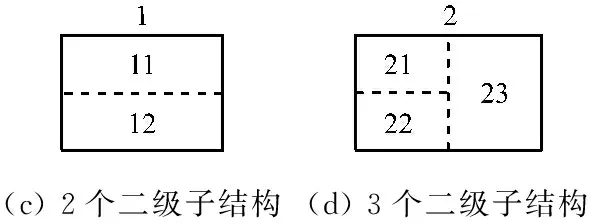
为便于说明，将整体结构划分为2个一级子结构，将其中一个一级子结构划分为2个二级子结构，将另一个一级子结构划分为3个二级子结构，如图1所示.图中1和2为一级子结构编号，11、12、21、22和23为二级子结构编号.

(a) 整体结构

(c)2个二级子结构(d)3个二级子结构

图1 子结构划分示意图

Fig.1 Division of substructures

1.1 二级子结构自由度的缩聚

在物理坐标下，二级子结构无阻尼有限元运动微分方程可表示为

(1)

式中：左上标ij为二级子结构的编号；ijM、ijK、iju、ijf分别为二级子结构ij的质量矩阵、刚度矩阵、位移向量和对接界面节点上由于子结构之间相互作用产生的节点力向量.

采用固定界面CMS法[10-11]缩聚二级子结构内部自由度，依据频率截止准则[11]，主模态选取该子结构的前K阶模态，二级子结构内部节点位移iju可以用二级子结构ij的主模态和约束模态表示为

ijuI=ijΨKijqK+ijΨCijuB

(2)

式中：ijΨK、ijΨC分别为二级子结构ij的固定界面主模态和约束模态；ijqK为二级子结构的模态坐标；ijuB为二级子结构交界面上节点的物理坐标.

该二级子结构的总位移可表示为

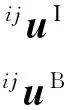
(3)

式中：ijΤ为二级子结构ij的坐标转换矩阵；ijq为二级子结构ij的模态坐标和交界面物理坐标组成的广义坐标向量.

将坐标转换关系式(3)代入式(1)中，并在方程两边左乘坐标转换矩阵的转置矩阵ijTT，可得广义坐标下该二级子结构无阻尼运动微分方程为

(4)

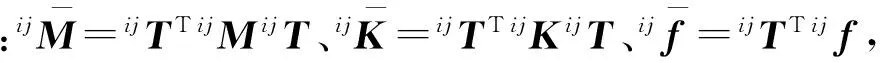
至此可实现二级子结构内部自由度的缩聚，降低了二级子结构运动微分方程的阶数.

1.2 一级子结构运动微分方程的形成

根据二级子结构间对接界面上力平衡和位移协调条件，组装二级子结构，可得到一级子结构在广义坐标下的运动微分方程为

(5)

式中：左上标i表示一级子结构的编号；iM、iK、iq、if分别为一级子结构i的广义质量矩阵、广义刚度矩阵、广义坐标向量和广义力向量.

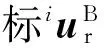
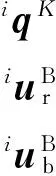
(6)

将式(5) 写成分块形式为

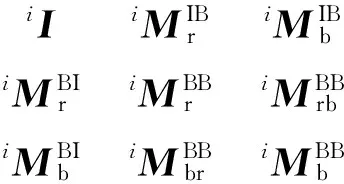
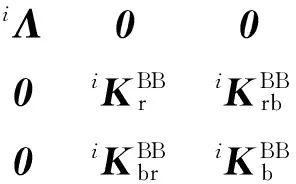
(7)

1.3 一级子结构二次降阶后的运动微分方程

(8)

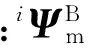
将坐标转换式(8)代入式(6)中，可以得到广义坐标向量iq和自由度进一步缩减后的广义坐标向量iP的关系式

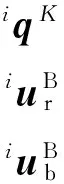
(9)

将式(9)代入式(7)中，得到一级子结构自由度进一步缩减后的无阻尼运动微分方程为

(10)

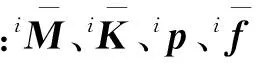
1.4 降阶后的系统运动微分方程及系统的模态求解

根据一级子结构间对接界面上力平衡和位移协调条件，组装一级子结构，可以得到整体系统在广义坐标下的无阻尼运动微分方程

(11)

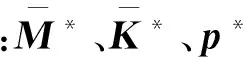
求解式(11)可得到整体系统的固有频率和广义坐标下的模态振型，再经过坐标反变换可得到系统在物理坐标下的模态振型.

2 1 000 MW汽轮发电机组转子-末级叶片耦合系统扭转振动计算

1 000 MW汽轮发电机组转子-末级叶片耦合系统结构见图2.采用前述分层二重CMS法计算了该转子-末级叶片耦合系统扭转振动特性，并计算了不考虑末级、次末级叶片实际结构(即仅考虑转动惯量)影响的轴系扭转振动特性.

2.1 子结构划分及降阶

采用三维六面体二次单元对整个转子、4级末级叶片和4级次末级叶片进行了网格划分，共划分了18 793 212个单元，51 865 985个节点.计算自由度数达到1.5×109，由于自由度数多，无法采用有限元法直接计算.

图2 1 000 MW汽轮发电机组转子-末级叶片耦合系统

考虑实际转子、轮盘和叶片连接的特点，将高压转子、中压转子、低压转子A、低压转子B和发电机转子分别划分为1个一级子结构；将4级次末级叶片系统划分为4个一级子结构；将4级末级叶片系统划分为4个一级子结构.共划分了13个一级子结构.将每个末级和次末级叶片系统又分别划分为7个二级子结构.由于篇幅所限，仅给出了高压转子子结构的有限元网格及其对应的超单元，如图 3所示.末级叶片的二级子结构及其对应的超单元如图 4所示.

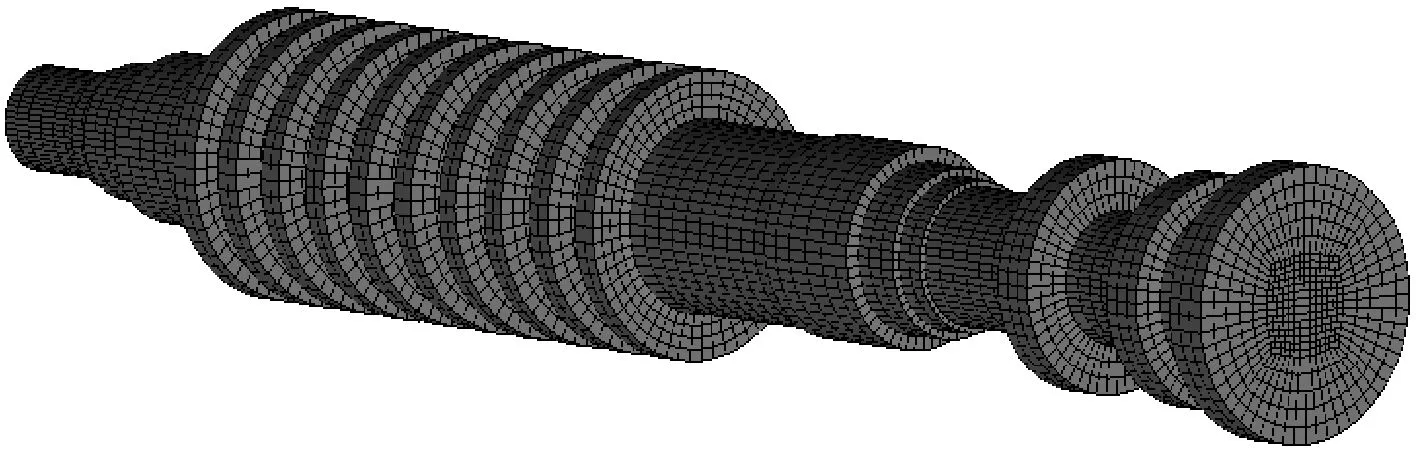
(a) 子结构

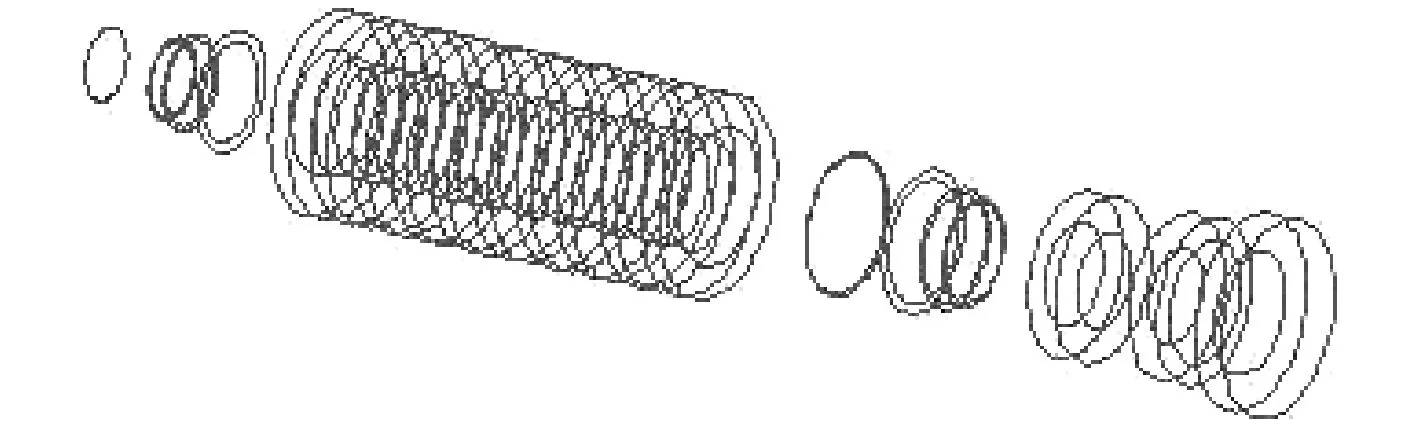
(b) 超单元

采用分层二重CMS法得到的转子-末级叶片耦合系统的自由度约为1.05×105，仅为原整个系统有限元分析所用自由度的0.07%.

2.2 计算结果及讨论

计算出的某1 000 MW汽轮发电机组转子、末级叶片和次末级叶片耦合系统扭转振动特性，以及仅考虑叶片转动惯量影响的轴系扭转振动固有频率见表1.

由表1可知，相比于仅考虑末级叶片转动惯量(非耦合系统)影响的轴系扭转振动模态，考虑末级叶片实际结构(耦合系统)的轴系扭转振动模态增加了一些新的模态.其原因在于：末级叶片零节径同相的切向振动和轴系扭转振动相当于一个串联系统，由振动力学可知，如果组成串联系统的2个元件的刚度相差较大，则只有刚度较小的元件所对应的刚度起主导作用；只有2个元件的刚度相差不大时，2个元件的刚度才会共同起作用.当末级叶片较短时，叶片的切向振动刚度远大于转子的扭转刚度，此时叶片切向振动和轴系扭转耦合作用较弱，分析轴系扭转振动时，仅考虑叶片转动惯量的影响即可，计算叶片振动特性时，也可忽略轴系的影响.然而，随着末级叶片长度的增加，成圈叶片切向刚度降低，成圈叶片零节径切向振动和转子扭转振动的耦合作用不能忽略.在末级叶片的零节径伞形振动频率降到110 Hz以内时，会在100 Hz附近出现由耦合作用造成的以叶片分支振动为主的轴系扭转振动.

(a) 子结构

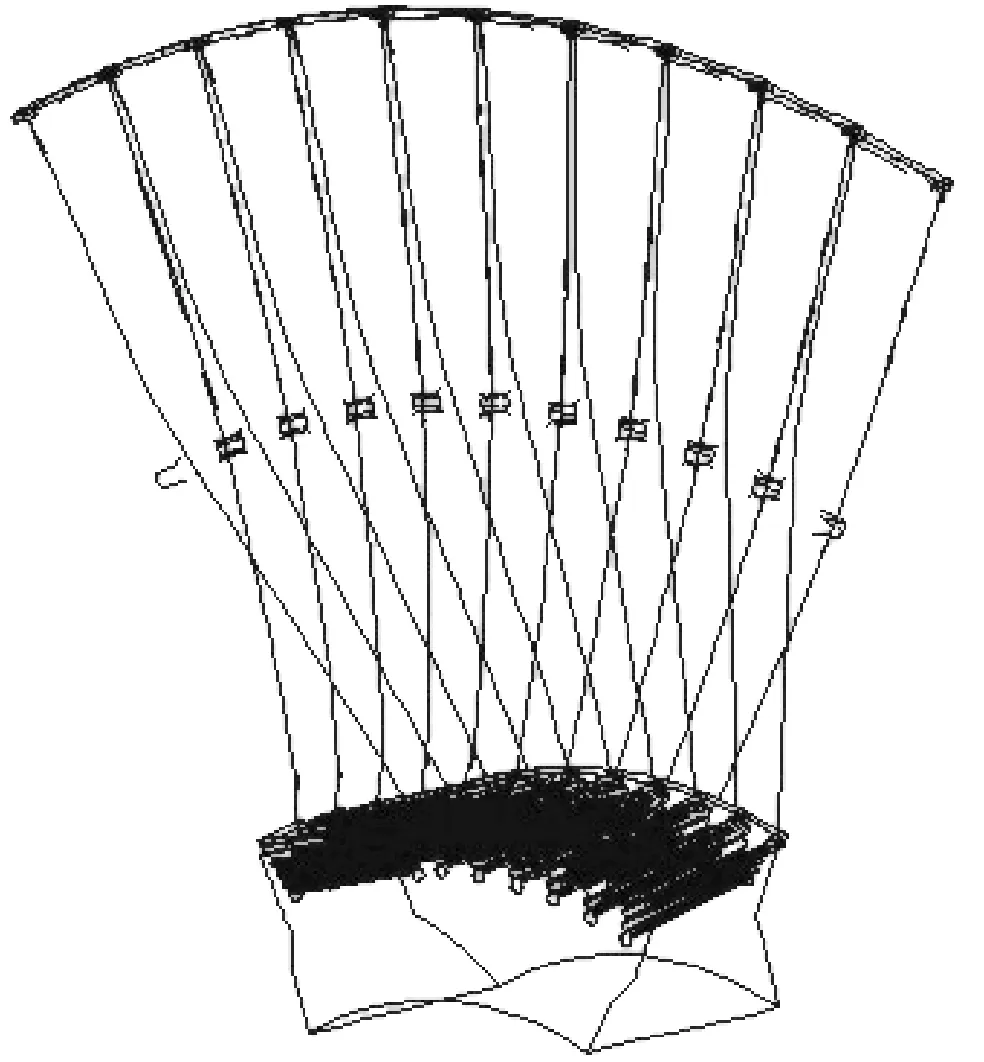
(b) 超单元

表1 轴系扭转振动固有频率计算结果

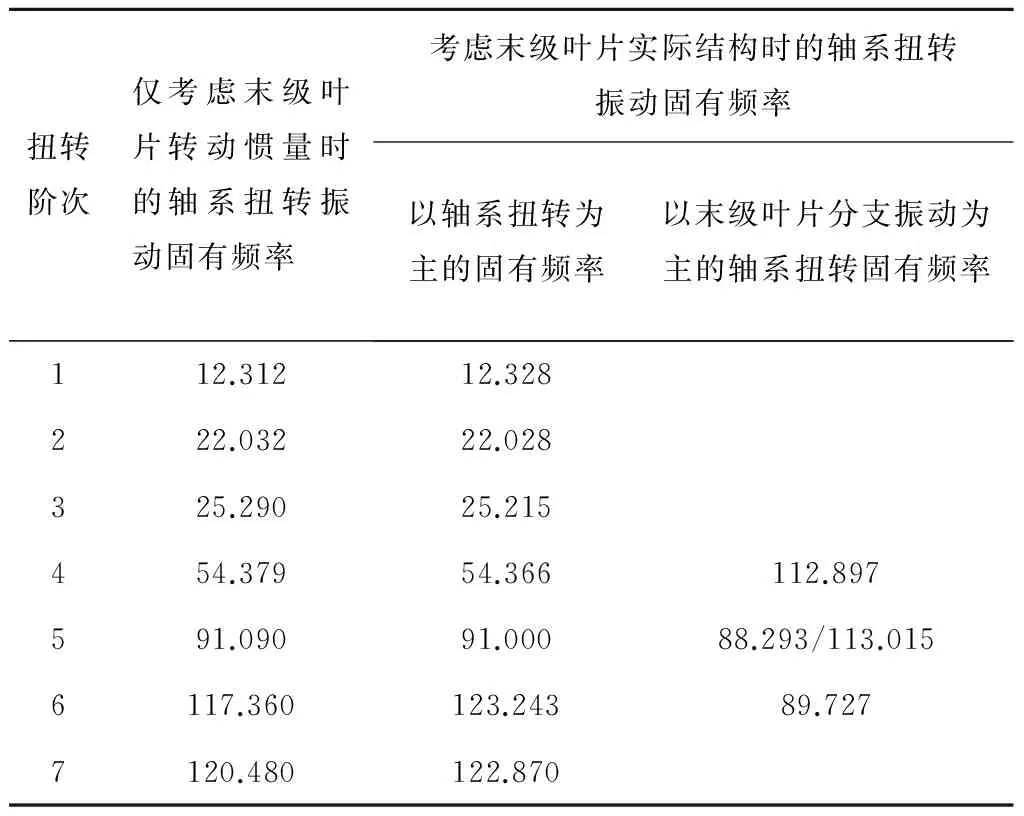
Tab.1 Calculated torsional vibration frequency of the rotor system Hz

采用考虑末级和次末级叶片实际结构以及仅考虑末级叶片转动惯量2种计算模型，得到以轴系扭转为主的第4阶～第7阶扭转振动主振型，如图5(a)～图5(d)所示.由图5(a)和图5(b)可以看出，2种模型计算出的固有频率和主振型基本一致，表明末级和次末级叶片结构的柔性对第4阶和第5阶以轴系扭转为主的扭转振动影响不大.第6阶非耦合系统的固有频率为117.36 Hz，而耦合系统的固有频率增大到123.24 Hz；第7阶非耦合系统的固有频率为120.48 Hz，而耦合系统的固有频率增大到122.87 Hz.耦合系统的主振型更加平缓，表明末级和次末级叶片结构的柔性对第6阶和第7阶以轴系扭转为主的扭转振动有影响.

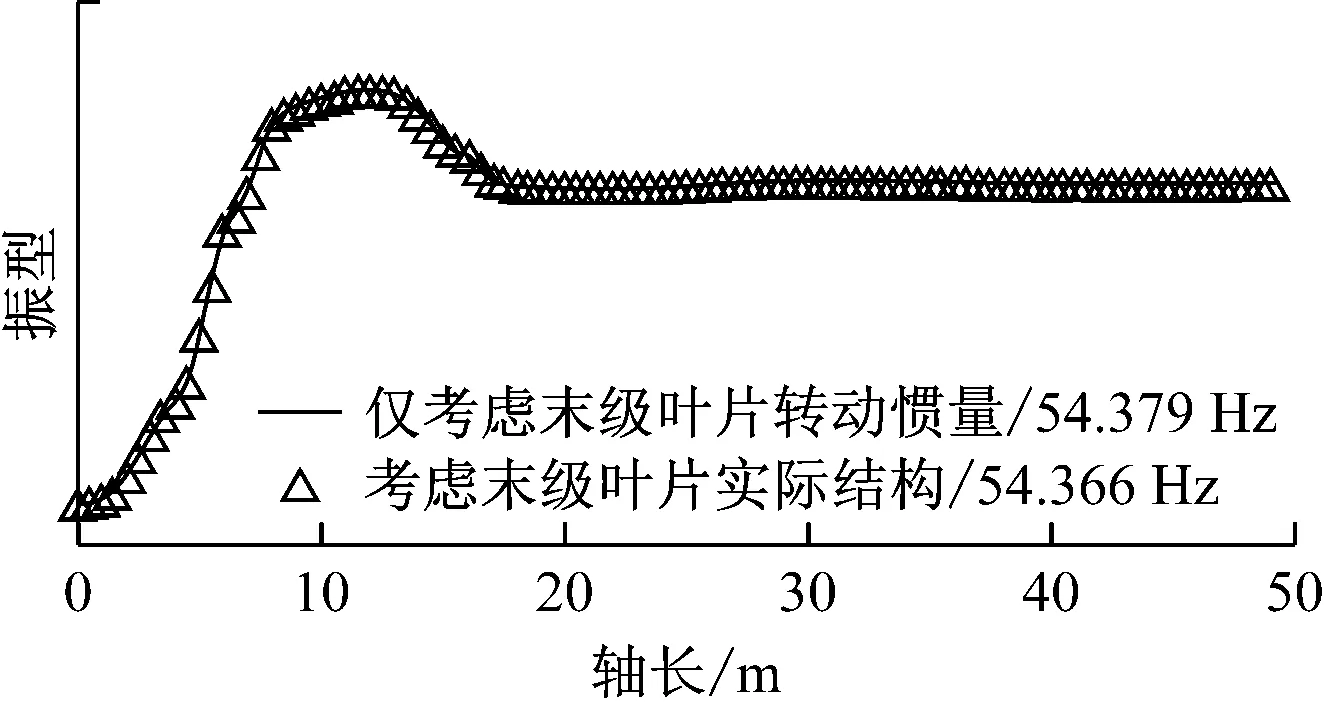
(a) 第4阶扭转振动

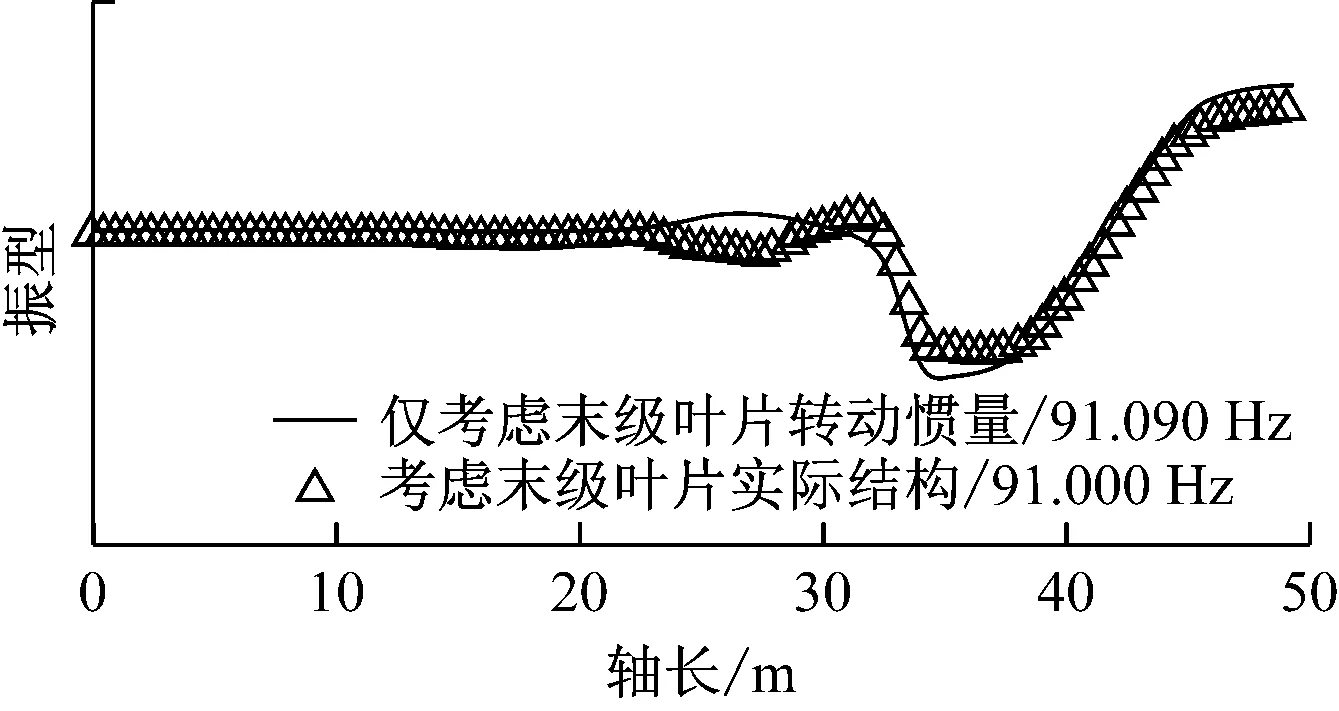
(b) 第5阶扭转振动

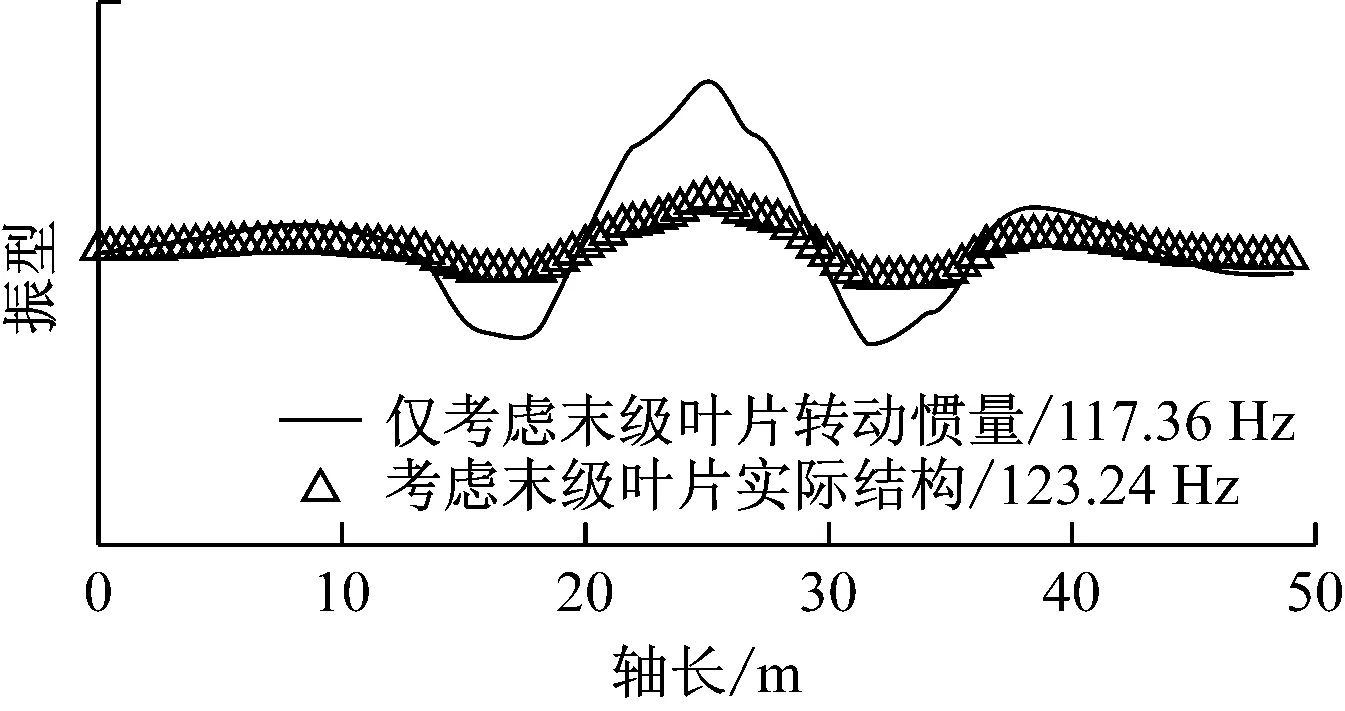
(c) 第6阶扭转振动

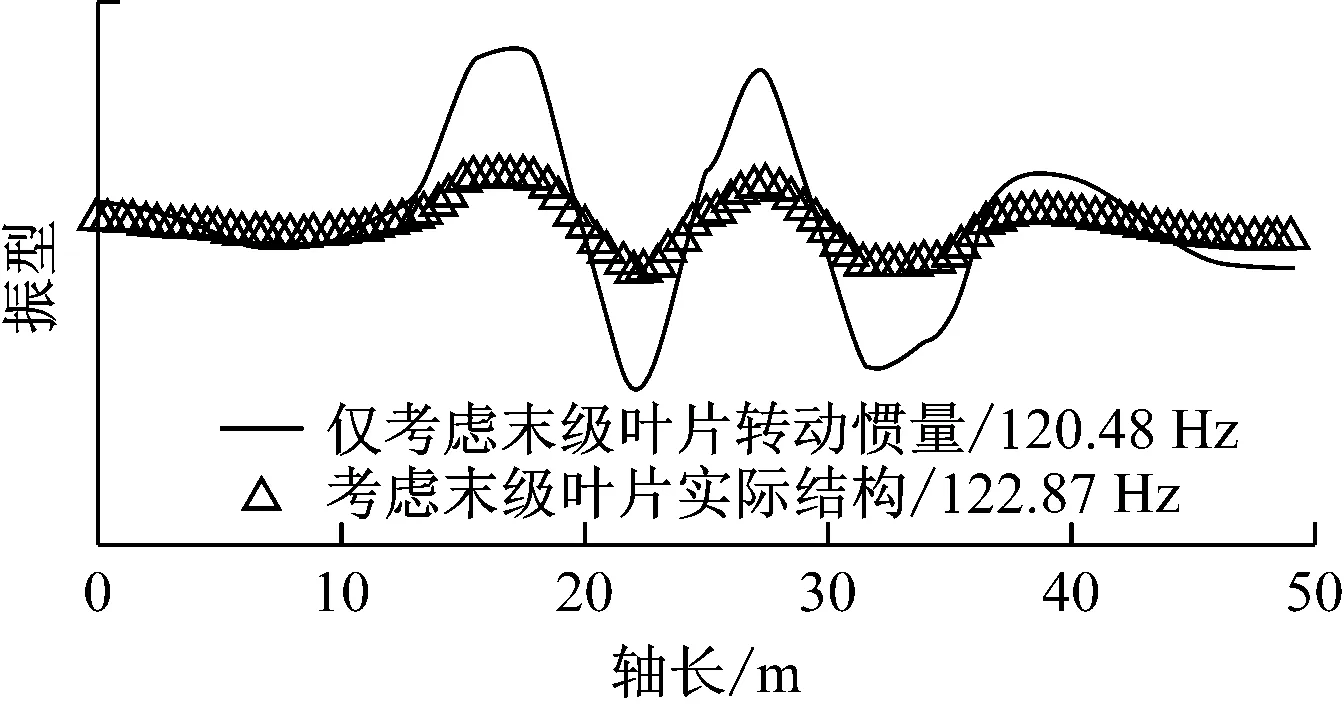
(d) 第7阶扭转振动

考虑末级和次末级叶片实际结构影响后新增1个第4阶扭转固有振动，其主振型见图6，扭转振型云图见图7.由图7可知，该振动是由末级叶片的分支振动引起的轴系扭转振动.进一步分析数据发现末级叶片的切向振动都与对应轴的扭转振动反相；4级末级叶片之间的切向振动是同相的.

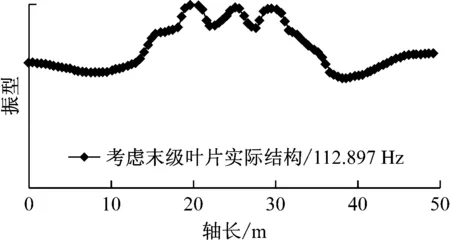
图6 末级叶片分支振动引起的轴系第4阶扭转振动

考虑末级和次末级叶片实际结构影响后新增2个第5阶扭转振动，其扭转振型见图8，扭转振型云图见图9和图10.由图9和图10可知，2个第5阶扭转振动都是由末级叶片的分支振动引起的轴系扭转振动.进一步分析113.015 Hz对应的主振型可知，末级叶片的切向振动都与对应轴的扭转振动反相；低压转子A上2级末级叶片的切向振动同相，低压转子B上2级末级叶片的切向振动同相；但低压转子A上2级末级叶片的切向振动与低压转子B上2级末级叶片的切向振动反相.分析88.293 Hz对应的主振型可知，末级叶片的切向振动都与对应轴的扭转振动同相；低压转子A上2级末级叶片的切向振动反相，低压转子B上2级末级叶片的切向振动反相.

图7 耦合系统频率为112.9 Hz的主振型云图

考虑末级和次末级叶片实际结构影响后新增1个第6阶扭转振动，其扭转振型见图11，扭转振型云图见图12.由图12可知，该振动也是由末级叶片的分支振动引起的轴系扭转振动.进一步分析数据可知，89.727 Hz对应的主振型中末级叶片的切向振动都与对应轴的扭转振动同相；低压转子A上2级末级叶片的切向振动反相，低压转子B上2级末级叶片的切向振动反相.

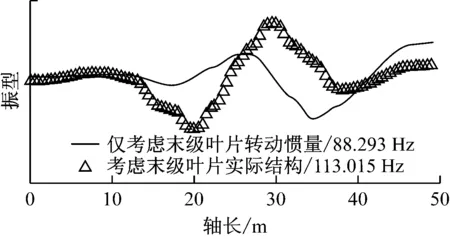
图8 叶片分支振动引起的轴系第5阶扭转振动

图9 耦合系统频率为113.015 Hz的主振型云图

图10 耦合系统频率为88.293 Hz的主振型云图

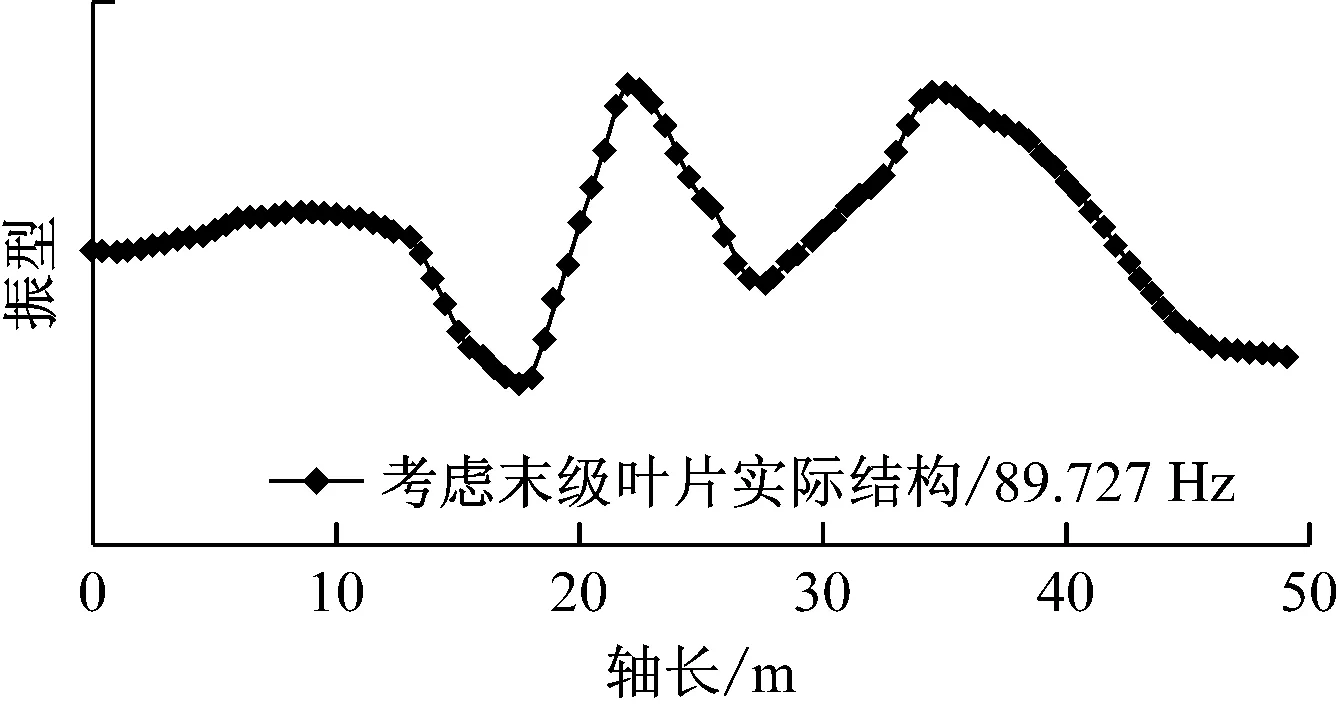
图11 叶片分支振动引起的轴系第6阶扭转振动

从以上分析可知，耦合以后，当成圈叶片零节径伞形振动的切向振动方向与对应轴部分的扭转振动同相时，叶片分支振动频率会变小；而当成圈叶片零节径伞形振动的切向振动方向与对应轴部分的扭转振动反相时，叶片分支振动频率会变大.

图12 耦合系统频率为89.727 Hz的主振型云图

该轴系上共有4级末级叶片，叶片分支振动引起的轴系扭转振动是由4级末级叶片分支振动共同作用的结果.4级末级叶片之间切向振动的同相、反相以及轴系其他部分的转动惯量和扭转刚度等因素决定了耦合系统轴系扭转振动的阶次.所以，轴系的扭转振动阶次并不与单级叶片分支振动的频率高低直接关联，因此出现了阶次高、频率低的现象.

3 结 论

在模态综合法的基础上，推导出计算转子-末级叶片耦合系统扭转振动的分层二重模态综合法的基本方程，给出了降阶的思路和原理.采用三维六面体二次单元对某1 000 MW汽轮发电机组转子、末级和次末级叶片系统进行了离散，系统自由度数达到1.5亿.采用分层二重CMS法计算了该转子耦合系统的扭转振动特性.考虑末级和次末级叶片实际结构的影响比不考虑实际结构影响时新增4个扭转固有振动,固有频率分别为88.293 Hz、89.727 Hz、112.897 Hz和113.015 Hz.这4个固有频率主要是由叶片分支振动引起的，且这些分支振动引起了整个轴系的扭转振动，它们分别引起了1个新的第4阶扭转固有振动，2个新的第5阶扭转固有振动和1个新的第6阶扭转固有振动.第6阶和第7阶以轴系扭转为主的固有频率比不考虑末级、次末级叶片实际结构时稍有增大.可见，如果不考虑末级叶片实际结构，会漏掉一些重要的振动模态，给转子和叶片的安全运行带来隐患.降阶后的系统广义自由度仅为原自由度的0.07%，突破了计算资源的限制，有效实现了转子耦合系统振动特性的计算与分析.

[1] 宋光雄, 陈松平, 宋君辉,等. 汽轮发电机组转子裂纹故障研究及分析[J]. 动力工程学报, 2012, 32(4): 289-295.

SONG Guangxiong, CHEN Songping, SONG Junhui,etal. Cause analysis of rotor cracks in turbine-generator units[J]. Journal of Chinese Society of Power Engineering, 2012, 32(4): 289-295.

[2] OKABE A, KUDO T, YODA H，etal. Rotor-blade coupled vibration analysis by measuring modal parameters of actual rotor[C]//Proceedings of ASME Turbo Expo 2009, Power for Land, Sea, and Air. Orlando, Florida, USA：International Gas Turbine Institute，2009：803-812.

[3] Standards Policy and Strategy Committee. BS ISO 22266-1:2009(E) mechanical vibration-torsional vibration of rotating machinery-part 1: land-based steam and gas turbine generator sets in excess of 50 MW[S]. Switzerland: ISO Copyright Office, 2009.

[4] ROSARIO D A, KHALID T. Generator shaft key way cracking failure investigation[C]//Proceedings of the 9th EPRI Steam Turbine/Generator Workshop. Denver, Colorado, USA：EPRI, 2005.

[5] 许楚镇, 张恒涛. 汽轮发电机组轴系扭振事故剖析和技术开发展望[J]. 动力工程, 1990, 10(2): 9-14.

XU Chuzhen, ZHANG Hengtao. An analytical review of torsional vibration failures of turbine-generator shafting system abroad and in China with a prospect of future development [J]. Power Engineering, 1990, 10(2): 9-14.

[6] 郭力, 朱均. 汽轮发电机组转子-轮盘-叶片系统耦合扭转振动研究[J]. 汽轮机技术, 2001, 43(4): 226-228.

GUO Li, ZHU Jun. The coupled torsional vibrations research of rotor-blade disk-vane system in steam turbine [J]. Turbine Technology, 2001, 43(4): 226-228.

[7] OKABE A, SHIOHATA K, KUDO T,etal. Rotor-blade coupled torsional vibration analysis using modal parameters based on FEM analyses and experiments[C]//Proceedings of ASME 2010 International Mechanical Engineering Congress & Exposition. Vancouver, British Columbia, Canada：ASME，2010.

[8] 鲍文, 王西田, 于达仁，等. 300 MW汽轮机低压缸末级长叶片与轴系扭振的耦合振动[J]. 汽轮机技术, 2000, 42(2): 65-68.

BAO Wen, WANG Xitian, YU Daren,etal. The coupling of the long blades at the final stage of the low pressure turbine with the shaft torsional vibrations [J]. Turbine Technology, 2000, 42(2): 65-68.

[9] 杨建刚, 高斖. 大型旋转机械叶片-轴弯扭耦合振动问题的研究[J]. 动力工程, 2003, 23(4): 2569-2573.

YANG Jiangang, GAO Wei. Research on the coupled blade-bending and shaft-torsion vibration of rotating machinery [J]. Power Engineering, 2003, 23(4): 2569-2573.

[10] 楼梦麟. 结构动力分析的子结构方法[M]. 上海：同济大学出版社, 1997.

[11] 王永岩. 动态子结构方法理论及应用[M]. 北京：科学出版社,1999.

Coupled Torsional Vibration Analysis of Shaft-Last Stage Blade System in Large Turbo-Generator Units Using CMS Method with Nested Substructures

XUZili1,DOUBaitong1,FANXiaoping2,FANGYu2,WANGJianlu2,CAOShouhong2

(1. State Key Lab for Strength and Vibration of Mechanical Structures, Xi'an Jiaotong University, Xi'an 710049, China; 2. Dongfang Turbine Co., Ltd., Deyang 618000, Sichuan Province, China)

To solve the problem of multi-degree of freedom and hard achievement in calculating the torsional vibration of coupled shaft-last stage blade system in large turbo-generator units with three-dimensional finite element method, major equations based on component mode synthesis (CMS) method with nested substructures were derived, while the thinking and principles of order reduction were given. Torsional vibration characteristics of a coupled system of rotor, last-stage and second last-stage disks and blades of a 1 000 MW turbo-generator unit were calculated and analyzed by the proposed method, of which the calculated results were compared with the torsional vibration modes of the entire shaft without considering the effect of actual structure of the last-stage and second last-stage disks and blades. Results show that some important natural modes would be neglected if the actual disk-blade structure is not considered, bringing hidden dangers to the safety of the rotor and blades. The degree of freedom of the entire system is about 150 million by 3D finite element method, which is only 0.07% of the original one after order reduction. The CMS method with nested substructure can be used to analyze the torsional vibration of a coupled system consisting of rotor, last-stage and second last-stage disks and blades of large turbo-generator units.

turbo-generator unit; shaft; CMS method with nested substructure; last stage blade; torsional vibration

1674-7607(2014)12-0938-07

TK263

A

470.30

2014-03-03

2014-04-28

国家973计划资助项目(2011CB706505); 国家自然科学基金资助项目(51275385)

徐自力(1967-), 男，山西运城人，教授，博士，研究方向为：能源动力装备结构强度与振动. 电话(Tel.): 029-82664686; E-mail: zlxu@mail.xjtu.edu.cn.