钛合金管冷弯回弹及其控制研究现状

宋飞飞，杨 合，杨英丽，吴金平，苏航标，罗媛媛，毛小南

(1. 西北有色金属研究院，陕西 西安 710016) (2. 西北工业大学 凝固技术国家重点实验室，陕西 西安 710072)



钛合金管冷弯回弹及其控制研究现状

宋飞飞1，杨 合2，杨英丽1，吴金平1，苏航标1，罗媛媛1，毛小南1

(1. 西北有色金属研究院，陕西 西安 710016) (2. 西北工业大学 凝固技术国家重点实验室，陕西 西安 710072)

钛合金管被广泛应用于航空航天等领域的液压管路系统中。然而，高的屈弹比会导致钛合金管冷弯后产生显著的回弹，而过度回弹会严重影响管路的装配及密封性能。为此，对近年来钛合金管冷弯回弹及其控制问题的研究工作与成果进行了综述，重点介绍了研究钛合金管冷弯回弹问题时通常采用的两种方法及相应的研究成果，主要包括理论解析法和有限元模拟法，并指出应对钛合金管材小角度下的弯曲及回弹进行深入研究，进一步提高管材弯曲理论研究的水平，将有限元模拟法与实验验证充分结合。

钛合金管；冷弯；回弹；控制

0 引 言

导管在飞机液压管路系统中有着广泛的应用，例如被用于油路、环控、冷却、供氧等，并且其可靠性及持久性对飞机的性能有着至关重要的作用。随着我国新一代先进飞行器的发展，迫切需要能够承受较大工作压力(如28 MPa，甚至32 MPa)的液压管路系统，以满足新一代飞机对机动性、稳定性和安全性等方面的要求。与常用不锈钢管或铝合金管相比，钛合金管具有质轻、高强、耐腐蚀、耐高温和长寿命等优异特性，将其用于液压管路系统，不仅能够承受更大的工作压力，还能满足航空航天领域对轻量化构件的需求[1-2]。

导管在使用时由于受到空间及装配要求的限制，需要对其进行弯曲。冷弯具有效率高、精度好的优点，是成形导管的主要方法。管材弯曲时外侧受拉、内侧受压，会产生管壁减薄、截面扁化及回弹等现象。其中，回弹是模具松开后管材弹性变形发生卸载造成的必然结果，使得成形角减小，成形半径增大。由于管材弯曲的特点，回弹时管材内外侧应力卸载，回弹效应叠加，导致弯管的回弹较板材显著。相比于铝合金、不锈钢等管材，钛合金管的屈弹比(屈服强度/弹性模量)更大[3]，造成钛合金管冷弯后的回弹现象更加显著(如图1所示[2])。而过度回弹会严重影响导管的成形精度，造成后续装配困难，影响管路系统的使用性能，因此，对回弹进行预测及控制是十分有必要的。为此，综述了目前钛合金管冷弯回弹及其控制问题的研究现状，在此基础上，指出了钛合金管冷弯回弹及其控制研究中存在的问题，相信对于发展钛合金管精确成形技术，进而对提高飞机性能有着重要意义。

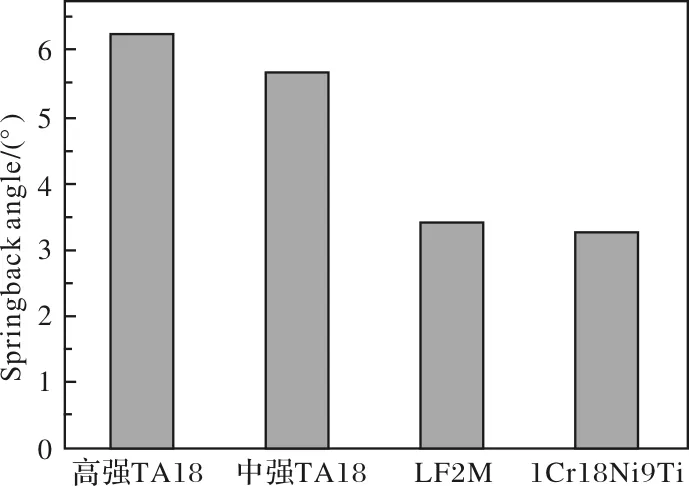
图1 不同材料管材的回弹角Fig.1 Springback angle of different material tubes

1 钛合金管冷弯回弹研究现状

目前，国内外学者多采用理论解析、有限元模拟和实验等方法对管材弯曲回弹问题进行研究。

在理论解析法研究方面，钛合金管的弯曲受力状态与其他材料管材一致，只是应力应变关系不同，因此可以借鉴其他常用管材的弯曲理论及分析思路。由于卸载后回弹过程是由弯曲结束时管材的应力应变状态决定的，因此计算弯曲结束时管材的应力应变是采用理论解析法研究回弹的首要工作。Al-Qureshi[4-5]根据梁的弯曲回弹理论推导了理想弹塑性弯管弯曲结束时的应力及弯矩，根据弹性卸载规律，推导了回弹和残余应力计算式，研究了管材外径、壁厚、屈服强度及弹性模量等参数对回弹的影响。熊淑元[6]对圆管的弯曲工艺、变形规律、失效形式以及回弹规律进行了理论分析，阐述了管材在弯曲力矩作用下弯曲时的受力情况及应力应变状态，并运用弹塑性弯曲理论推导了弯曲力矩与曲率之间的变化关系，阐述了管材在弯曲加工全过程中弯曲角与成形角之间的变化关系。刘光武等人[7]将理想弹塑性材料的弯曲回弹分为一次回弹与二次回弹两个阶段，并进行了应力应变分析，根据应力平衡条件和变形协调条件推导出了回弹曲率、回弹弯矩等一系列计算式，并进行了回弹误差估计，然后在弯矩假设模型的基础上，推导出任意弯曲加工角度时管材的回弹规律。但是，由于上述研究假设太多，仅仅考虑了弯曲切向应力应变，使计算求解结果与实验结果偏差较大。

张立玲[8]通过对管材弯曲条件下的应力应变分析，推导了幂指数硬化材料弯管弯矩的计算式，并根据回弹理论与卸载前后中性层不变的条件，推导了回弹角以及回弹半径补偿量的计算式。Li[9]通过塑性变形理论与横截面不变等假设，忽略钛合金管的壁厚变化，采用弹塑性硬化模型，推导了回弹半径和回弹角度计算公式。虽然上述研究采用与钛合金材料硬化规律近似的幂指数硬化模型来求解，但仅考虑了弯管的切向应力，忽略了其立体应力应变状态。

Normani[10]基于全量理论建立了管材拉弯过程的解析模型，并根据梁弯曲的弹性卸载理论建立了回弹解析模型，通过数值方法求解整个分析过程。但是，研究中将弯管截面周向应变简化为了一个经验函数式，也没有考虑弯曲成形中的弹性变形以及材料的各向异性。

由于理论解析法往往存在大量假设条件，例如，没有考虑管材弯曲过程中的摩擦、内外侧壁厚变化、截面扁化及中性层偏移现象、假设管材为理想弹塑性或弹塑性硬化材料等，这些假设使求解精度和实用性受到一定限制。近年来，随着塑性成形有限元法和计算机技术的逐步发展，有限元法以能够处理复杂非线性问题而被广泛应用于研究材料弯曲回弹过程。而有限元模拟中的数值参数及材料模型对回弹计算精度的提高极为关键[11]。其中，数值参数包括单元类型、厚向积分点个数、求解算法等。Li[12]和Wagoner[13]进行了三种板材典型工艺下的一系列拉弯过程模拟，发现提高厚向积分点个数、细化与模具接触的单元网格以及采用3D壳单元和非线性实体单元能够提高回弹预测精度，并且，随着弯曲半径减小，回弹预测最大误差会增大。Papeleux[14]发现显式或隐式求解算法除了对计算成本有影响以外，对回弹计算结果影响不大。然而，在有限元法数值参数选取方面，大量研究都以板材为研究对象，在管材弯曲回弹方面，特别是关于钛合金管的研究却很少。Jiang[15]建立了钛合金管绕弯三维有限元模型，讨论了显式计算时单双精度及质量放大因子选取对弯曲结果的影响。Song[16]基于Abaqus平台建立了钛合金管数控弯曲三维弹塑性有限元弯曲和回弹模型，系统地研究了管材单元类型、管壁厚向积分点个数、单元尺寸、阻尼因子等显式算法及隐式算法数值参数选取对钛合金管冷弯回弹模拟精度及效率的影响。上述研究对钛合金管冷弯回弹有限元建模具有一定的指导作用。

对于材料模型，目前国内外学者在这一方面作了大量研究工作，包括屈服准则、塑性本构方程及弹性卸载行为。对于屈服准则，Mises各向同性屈服准则应用最为广泛，然而，钛合金管在轧制过程中产生的织构将导致性能的各向异性，因此，Hill’1948各向异性屈服准则因表述简单也被广泛应用于弯曲回弹研究[17]。为了更加精确地描述铝合金板及钢板的弹性或塑性各向异性行为，提出了Hosford、Barlat’1989、Barlat’2005等屈服准则[18]。在硬化规律方面，采用非线性随动强化硬化模型可以提高板材回弹预测精度[19]。考虑非线性回弹及变弹性模量，也被证实可以提高回弹预测精度[18]。然而，一方面，由于上述研究基本上只针对铝合金板或钢板的拉弯或冲压回弹，对于其他材料、弯曲方式及截面形式的研究少之又少，如钛合金管材的弯曲回弹；另一方面，采用复杂的先进模型所带来的求解成本远大于所提高的预测精度。因此，上述两方面原因造成目前在对钛合金管冷弯回弹有限元研究时仍广泛采用经典的Hill’1948各向异性屈服准则、等向强化模型及线性回弹定律。

西北工业大学杨合教授的团队在钛合金管冷弯回弹规律方面进行了大量研究。岳永保[20]模拟研究获得了退火态TA18(TA18M)钛合金管的弯曲回弹规律，发现当弯曲角大于30°后，弯曲角与回弹角呈线性关系。Jiang[21]采用逐步回归分析法对弹性模量、屈服强度、硬化指数、厚向异性指数等材料参数与弯曲角度耦合作用下的TA18M钛管弯曲回弹进行了模拟研究与分析，发现在弯曲角增大的情况下，弹性模量和硬化指数对回弹角有较大影响。王艳等人[22]基于Abaqus平台，模拟研究了去应力退火TA18钛管弯曲卸载回弹规律及回弹对壁厚减薄和截面扁化的影响，发现去应力退火态管材回弹量大于退火态，回弹对壁厚减薄的影响不显著，对截面扁化有显著影响。宋飞飞等人[23]模拟发现TA18钛管回弹角随芯棒伸出量的增大而减小，随弯曲模-管材摩擦系数、压块-管材间隙和芯棒-管材间隙的增大而增大，当压块相对助推速度小于1时，回弹角明显增大。Li[9，24]研究了TA18钛管回弹的弯曲回弹特性，发现材料是影响回弹的关键因素，并发现回弹半径在某一临界角度之前随弯曲角的增大而迅速减小，在该临界角度之后保持不变。在小角度弯曲时回弹角随弯曲角呈非线性变化，且该角度随弯曲半径的减小而增大。上述研究获得了材料参数、工艺参数对钛合金管冷弯回弹的影响规律，对实际弯曲回弹预测方面具有理论指导意义。

有限元法的应用，使得钛合金管冷弯回弹研究取得很大进展，模拟出的结果更加接近实际。然而，有限元模拟中定义的载荷、接触摩擦等边界条件，由于过于理想化，与实际管材弯曲过程中的状况还存在差别，因此，需要结合实验来进行验证。

2 钛合金管回弹控制研究现状

研究钛合金管弯曲回弹的目的是为了对其进行控制，调整弯曲工艺，使卸载后钛合金管的最终形状及尺寸满足使用要求。常用的管材弯曲回弹的控制方法主要有拉弯法和过弯法。拉弯法是在零件弯曲时施加拉力，改变弯曲零件的应力状态和分布情况，减小厚度方向应力梯度，减小弯曲力矩，减小卸载后内外层回弹叠加的趋势，从而可以显著减小弯曲回弹。Schmoeckel[25]研究了双向拉应力下的回弹，发现拉应力可以减小回弹，并且可以通过调整压边力来控制回弹，并通过实验验证了有限元模型。Gu[26]研究了施加轴力对管材弯曲回弹的影响，发现可以通过在弯曲时施加轴向拉力或压力，或在弯曲后施加轴向拉力来减小薄壁管的弯曲回弹。

由于钛合金管的回弹较为显著，且不能一味地增大拉力，否则会增加管壁弯曲开裂的倾向，而拉弯法的控制效果有限，因此常常采用过弯法来进行回弹角度的控制。过弯法是通过改变弯曲模转角，使得管材过量弯曲，借此使得回弹后的管材形状符合精度要求的补偿方法。Li[27]通过测量弯矩大小、压块运动位置和芯棒与管材摩擦来预测回弹。美国伊顿公司[28]将弯曲角与回弹角做近似线性关系处理，在弯管机上按120°和20°弯曲管材，然后测出其实际成形角，建立经过这两点的直线方程便可获得弯曲角与管材所需成形角之间的关系，该方法称为20°-120°法。在此基础上，Lou[29]提出了双线性补偿法，对小角度非线性回弹和大角度线性回弹分别采用直线拟合，精度较20°-120°法好。

在空间弯管时，不仅仅是回弹角，回弹半径的大小同样会影响弯管件成形精度。因此，修模法可以用来补偿弯管的回弹半径，即在弯曲模设计时预先考虑弯管件的回弹半径，修改模具尺寸，使得生产出的弯管件在回弹之后形状达到精度要求。Li[9]研究发现钛合金管回弹半径随弯曲半径的增大而增大，且达到某弯曲角度后保持不变，并提出了一种先补偿回弹半径再补偿回弹角的钛合金管弯曲回弹顺序补偿方法，该方法可以同时考虑回弹半径和回弹角度的补偿，提高补偿效率。这种方法在大角度弯曲时回弹补偿效果更好。

3 研究中存在的问题

(1)目前，国内外学者对铝合金、不锈钢等管材的回弹问题进行了大量研究，且多关注于角度回弹，然而钛合金管在小角度弯曲时回弹角与弯曲角呈非线性关系，且钛合金管回弹半径远大于同规格其他管材。因此，有必要对钛合金管材小角度下的弯曲及回弹进行深入研究，特别是在需要进行空间弯曲时。

(2)理论解析法虽然需要大量假设，但却能定性地认识回弹的内在机理，甚至定量地计算回弹结果。因此，应进一步提高管材弯曲理论研究水平，尽可能地考虑立体应变状态、中性层偏移及接触条件等。

(3)将有限元模拟法与实验验证相结合，仍是目前研究钛合金管回弹及控制的主要手段。因此，首先应研究建立能真实反映钛合金管冷弯回弹过程材料流动的屈服准则及本构方程。在此基础上，正确选取有限元数值参数、提高接触摩擦边界条件处理精度，可以提高有限元回弹预测精度，提升回弹控制效率。

[1]Yang H, Zhan M, Liu Y L, et al. Some advanced plastic processing technologies and their numerical simulation[J]. Journal of Materials Processing Technology, 2004, 151(1/3): 63-69.

[2]Yang H, Li H, Zhang Z Y, et al. Advances and trends on tube bending forming technologies[J]. Chinese Journal of Aeronautics, 2012, 25(1): 1-12.

[3]Mackenzie P M, Wakler C A, Mckelvie J. A method for evaluating the mechanical performance of thin-walled titanium tubes[J]. Thin-Walled Structures, 2007, 45(4): 400-406.

[4]Al-Qureshi H A. Elastic-plastic analysis of tube bending[J]. International Journal of Machine Tools and Manufacture, 1999, 39(1): 87-104.

[5]Al-Qureshi H A, Russo A. Spring-back and residual stresses in bending of thin-walled aluminum tubes[J]. Materials & Design, 2002, 23(2): 217-222.

[6]熊淑元. 圆管弯曲的弯曲变形规律和弯曲回弹的研究[D]. 重庆：重庆大学, 2001.

[7]刘光武, 胡勇, 王呈方. 弯管回弹的理论分析[J]. 武汉理工大学学报, 2007, 29(2): 136-138.

[8]张立玲. 管材塑性弯曲回弹量计算[J]. 锻压技术, 2002(3): 37-39.

[9]Li H, Yang H, Song F F, et al. Springback characterization and behaviors of high-strength Ti-3Al-2.5V tube in cold rotary draw bending[J]. Journal of Materials Processing Technology, 2012, 212(9): 1973-1987.

[10]Normani F V. Analytical modeling of tube bending with hydroforming[D]. Canada: Waterloo University, 2004.

[11]Li K P, Carden W P, Wagoner R H, et al. Simulation of springback[J]. International Journal of Mechanical Sciences, 2002, 44(1): 103-122.

[12]Li K, Geng L, Wagoner R H.Simulation of Springback: Choice of Element[C]//Advanced Technology of Plasticity 99: Proceedings of the 6th ICTP.Bavaria, Germany, 1999:2091-2098.

[13]Wagoner R H, Li M. Simulation of springback: through-thickness integration[J]. International Journal of Plasticity, 2007, 23(3): 345-360.

[14]Papeleux L, Ponthot J P. Finite element simulation of springback in sheet metal forming[J]. Journal of Materials Processing Technolgy, 2002, 125-126(9): 785-791.

[15]Jiang Z Q, Yang H, Zhan M,et al. Establishment of a 3D FE model for the bending of a titanium alloy tube[J]. International Journal of Mechnical Science, 2010, 52(9): 1115-1124.

[16]Song F F, Yang H, Li H, et al. Springback prediction of thick-walled high-strength titanium tube bending[J]. Chinese Journal of Aeronautics, 2013, 26(5): 1336-1345.

[17]Hill R. A theory of the yielding and plastic flow of anisotropic metals[J]. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1948, 193(1033): 281-297.

[18]Zhu Y X, Liu Y L, Yang H, et al. Development and application of the material constitutive model in springback prediction of cold-bending[J]. Materials & Design, 2012, 42(12): 245-258.

[19]Wagoner R H, Lim H, Lee M G. Advanced issues in springback[J]. International Journal of Plasticity, 2013, 45(6): 3-20.

[20]岳永保. 钛合金管弯曲成形过程数值模拟及实验研究[D]. 西安：西北工业大学, 2009.

[21]Jiang Z Q, Yang H, Zhan M, et al. Coupling effects of material properties and the bending angle on the springback angle of a titanium alloy tube during numerically controlled bending[J]. Materials & Design, 2010, 31(4): 2001-2010.

[22]王艳, 杨合, 李恒，等. 数控弯曲下TA18高强钛管回弹对壁厚减薄和截面畸变的影响[J]. 稀有金属材料与工程, 2012, 41(7): 1221-1225.

[23]宋飞飞, 杨合, 李恒，等. TA18高强钛管数控弯曲回弹工艺参数影响的显著性分析[J]. 稀有金属材料与工程, 2013, 42(1): 43-48.

[24]Li H, Yang H, Song F F, et al. Springback nonlinearity of high-strength titanium alloy tube upon mandrel bending[J]. International Journal of Precision Engineering and Manufacturing, 2013, 14(3): 429-438.

[25]Schmoeckel D, Beth M. Springback reduction in draw-bending process of sheet metals[J].CIRP Annals-Manufacturing Technology,1993, 42(1): 339-342.

[26]Gu R J, Yang H, Zhan M, et al. Springback of thin-walled tube NC precision bending and its numerical simulation[J]. Transactions of Nonferrous Metals Society of China, 2006, 16(S2): 631-638.

[27]Li H Z, Fagerson R, Stelson K A. A Method of adaptive control of rotary-draw thin-walled tube bending with springback compensation[C]//22nd North American manufacturing research conference, NAMRC XXII. Evanston, the United States,1994: 25-28.

[28]胡勇, 王呈方. 弯管工艺中回弹、伸长和成形半径的确定方法[J]. 锻压机械, 1997(1): 35-37.

[29]Lou H, Stelson K A. Three-dimensional tube geometry control for rotary draw tube bending, part 1: bend angle and overall tueb grometry control[J]. Journal of Manufaturing Science and Engineering, 2001, 123(2): 258-265.

Research Status in Springback and its Control of Titanium Alloy Tube Cold-bending

Song Feifei1, Yang He2, Yang Yingli1, Wu Jinping1, Su Hangbiao1, Luo Yuanyuan1, Mao Xiaonan1

(1.Northwest Institute for Nonferrous Metal Research，Xi’an 710016, China)(2.State Key Laboratory of Solidification Processing, Northwestern Polytechnical University, Xi’an 710072, China)

Titanium alloy tubes(Ti-tube) have been widely used in hydraulic plumbing systems of aircraft and spacecraft. However, significant springback of Ti-tube occurs after unloading due to its high ratio of yield strength to Yong’s modulus. The severe springback affects the connection and sealing performance of tubes with other parts. Therefore, the present research and findings of Ti-tube springback as well as its control are reviewed, while the methods of theory analysis and finite element simulation are introduced respectively. Finally, it is pointed out that bending and springbank beheavior under small angle for Ti-tube needs further investigation, and the level of theory research also needs to be improved.Besides, the methods of finite element simulation and experiment can be combined during the research.

titanium alloy tube; cold-bending;springback; control