数控加工中心维修时间模型研究

张海波，刘 亮，黄洋洋

(东北电力大学 机械工程学院，吉林 吉林 132012)

数控加工中心维修时间模型研究

张海波，刘 亮，黄洋洋

(东北电力大学 机械工程学院，吉林 吉林 132012)

因数控加工中心故障造成的停机是影响其工作效率的一个主要因素。为提高加工中心的工作效率，减少维修时间，文章运用origin8的绘图和Matlab的编程计算功能对某型号数控加工中心故障维修时间数据进行分析。首先绘制了加工中心故障维修时间的概率密度函数，然后由概率密度函数图形判断该函数可能符合的分布规律并进行参数估计，最终证明该型号数控加工中心故障维修时间符合对数正态分布规律，结合函数性质及故障数据，提出了减少数控加工中心维修时间的方法，为加工中心的维修提供了依据。

数控加工中心；维修时间模型；对数正态分布

0 引言

现代制造技术的快速发展使得数控机床越来越广泛的被机械加工企业所采用[1]。随着数控机床可靠性增长技术的发展，可靠性设计使得故障大大减少，但故障仍会不可避免的发生[2-3]。

维修性指维修的难易程度，它是影响数控机床寿命周期费用的重要因素[4]。数控机床维修性的研究建立在大量的故障数据基础之上，需要对其进行收集、选择、分析等步骤才能获得结论。在数控机床使用中需要处理好其维修、维护及备件管理等问题，而由于大多数数控机床用户缺乏专业的维修人员或维修人员经验不足等多种原因限制了数控机床性能的发挥[5]。为了更好的提高数控机床的工作效率，需要对数控机床的故障数据进行分析，以便快速提高其维修性能。

不同的数控机床有其各自不同的故障特点，故障维修时间也有较大差距，不同的数控机床应对应不同的维修方式及策略。本文对某型号9台数控加工中心故障维修时间数据进行了为期1年的跟踪，记录得到了92组数据并对其进行研究，按不同的故障维修时间将数据分类并用origin8软件绘制维修时间概率密度函数和维修时间分布函数图形；通过观察两组函数的图形和经验判断维修时间分布规律应符合正态分布或对数正态分布；最后应用Matlab编程求得各参数值，并进行K-S检验，得出了维修时间函数的分布规律，根据其分布规律制定了维修计划，起到减少维修时间、提高数控机床工作效率的目的。

1 维修时间模型的初步计算与预测

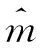
(1)

其中：ni-每组所含维修时间观测值的频数

n-维修时间观测值的总频数，共92组数据

Δti-组距，组距为10(min)

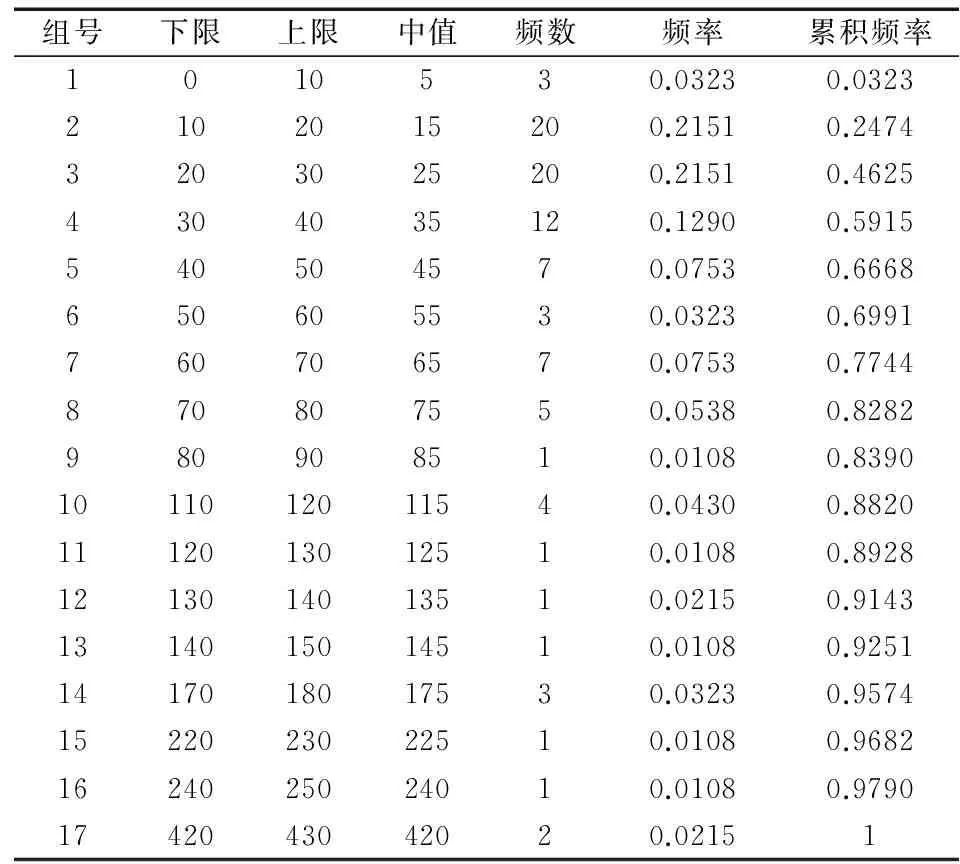
表1 数控加工中心故障维修时间频率及累计频率

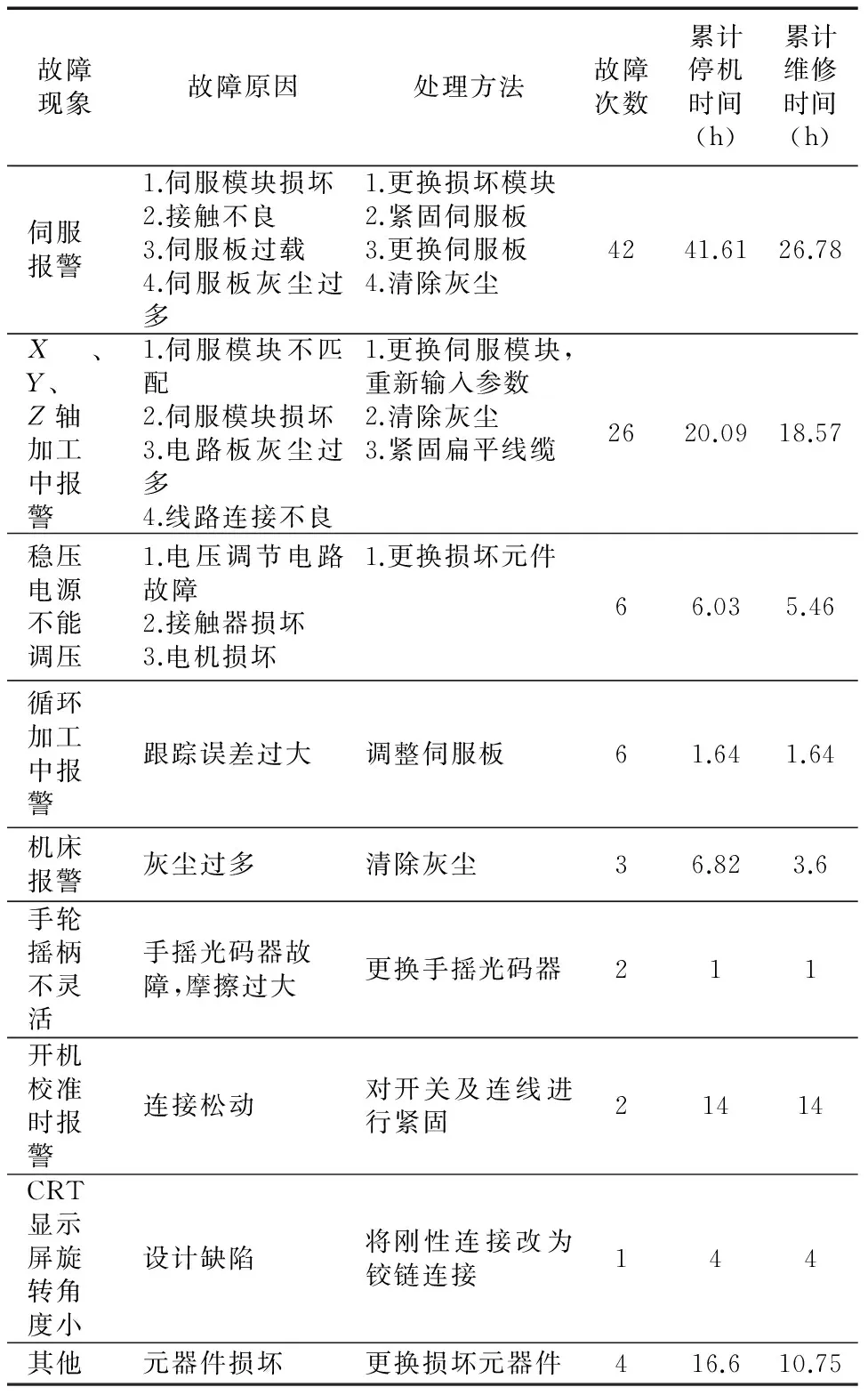
表2 数控加工中心故障分类表

使用origin8画出维修时间概率密度函数m(t)和分布函数M(t)的直角坐标散点图[6-7]，图中以每组中值为横坐标，分别以每组的频率和累积频率为纵坐标画得图1和图2。

数控加工中心维修时间概率密度函数整体呈单峰型，个别位置有出现跳动可能是由于数据在采集过程中出现的误差或受其他因素影响造成，在图像的起始部分存在维修时间频率的快速升高，维修时间分布函数呈凸型，将两图与常见的分布曲线相比较，同时根据经验判断该分布可能是正态分布或对数正态分布，其中对数正态分布的可能性更大。

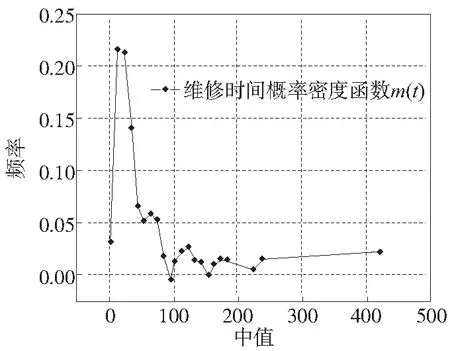
图1 维修时间概率密度函数m(t)

图2 维修时间分布函数M(t)

2 维修时间分布的参数估计

由于判断维修时间分布模型可能是正态分布或对数正态分布，所以采用极大似然估计的方法对其进行参数估计[8-9]。

当维修时间的分布类型是正态分布时，计算过程如下：

(2)

将公式2两侧同时取对数，得到：

(3)

解极大似然方程组

(4)

得到正态分布的参数估计公式

(5)

同理得到对数正态分布的参数估计公式

(6)

使用Matlab软件编程计算(Matlab程序略)，如果数控加工中心故障维修时间服从正态分布，则参数μ=44.1698、σ2=1.6512；如果数控加工中心故障维修时间服从对数正态分布，则参数μ=3.4904，σ2=0.6089。

3 维修时间模型的检验

假设数控加工中心维修时间模型是正态分布或对数正态分布，分别计算各维修时间的点估计值，并对假设执行K-S检验，检验方法：将数据按由小到大的次序排列，根据假设的分布，计算每个数据对应的F0(xi)，将其与经验分布函数Fn(xi)进行比较，其中差值的最大绝对值即检验统计量Dn的观察值。将Dn与临界值Dn,α进行比较。满足下列条件，则接受原假设，否则拒绝原假设[10]。

(7)

式中：F0(x)—原假设分布函数；

Fn(x)—样本大小为n的经验分布函数；

(8)

(9)

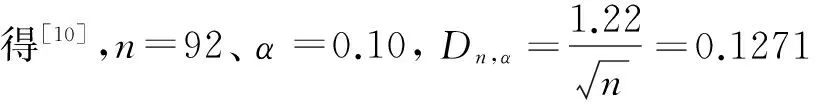
表3 假设检验结果对比

由K-S检验原理，假设维修时间模型服从正态分布，Dn=0.1456>Dn,α，所以该假设不成立；假设维修时间模型服从对数正态分布，Dn=0.1268

该加工中心维修时间的概率密度函数m(t)，维修时间分布函数M(t)，不可维修度函数G(t)，维修率函数u(t)，如下：

(10)

(11)

(12)

(13)

由对数正态分布的图形性质可知，大量的维修时间集中于某一范围，其他的维修时间则较为分散，同时也说明某一类故障发生频率较其他故障要高很多，因此需要加强对此类较多故障的预防与维修。

由表2可知该型号数控加工中心的主要故障是外购外协件质量问题和装配问题引起的伺服和各轴系统故障，除以上两点外灰尘堆积造成的通讯故障也是其中一类比较重要的故障。基于以上分析可以从以下三个方面采取措施：①加工中心生产厂商对外购外协件供应商的选择应在多家择优选取，同时其质量检验部门应明确产品的技术、质量标准等细节，并严格执行外购外协件的入厂检验工作；②生产厂商在对加工中心进行装配工作前要对零件进行清洗、去毛刺等工序以保证零件质量，并对旋转部件作动平衡试验，在装配中要使用专业工具并做好零部件的保护工作，装配完成后还要检测装配精度是否符合要求；③生产厂商应改善加工中心的防尘设计，尽量防止灰尘进入机床内部，使用方应注意环境的湿度和温度等条件，并定期清扫防止灰尘积累造成停机。

4 结论

本文采用origin8软件进行数控加工中心故障维修时间的绘图工作，运用Matlab编程计算其故障维修时间的分布函数并对其进行检验，最终确定该型号加工中心故障维修时间分布函数符合对数正态分布。造成该型号数控加工中心故障的主要原因是外购外协件质量问题、装配质量问题引起的伺服系统故障和各轴故障，此外还有灰尘堆积造成的通讯故障，在平时的数控加工中心维护中尤其需要注意这三方面问题，以提高数控加工中心的工作效率。

[1] 梁铖，刘建群.五轴联动数控机床技术现状与发展趋势[J].机械制造，2010,48(545)，5-7.

[2] Chen Diansheng, Jia Yazhou,Shen Guixiang. Probability Distribution of the Early Failures of Machining Centers[C]. Proceedings of the Sixth International Conference on Progress of Machining Technology,Xian,china,2002.

[3] Yi Dai, Yazhou Jia. Reliability of a VMC and its Improvement[J].Reliability Engineering and System Safety, 2001,72:99-102.

[4] 秦英孝.可靠性维修性保障性管理[M].北京：国防工业出版社，2003.

[5] 李文耿.数控机床维修性研究[J].中国城市经济，2010(9):139-142.

[6] 朱海涛，陈少秀，蔡华,等.origin软件在药学研究数据作图中的应用[J]. 医药导报,2008,27(9):1089-1091.

[7] 邓晓敏，张军朋，吴先球.利用origin确定试验中非线性函数的曲线关系[J].大学物理实验,2011,24(1):73-76.

[8] 王娜，李新海. 关于对数正态分布参数极大似然估计的讨论[J].北华大学学报(自然科学版),2007,8(5):394-397.

[9] 王蓉华，徐晓玲，费鹤良.对数正态分布参数的近似极大似然估计[J].上海师范大学学报,2000,29(1):39-43.

[10]贺国芳,许海宝. 可靠性数据的收集与分析[M]. 北京：国防工业出版社，1995.

(编辑 李秀敏)

Maintain Time Model of CNC Machining Center

ZHANG Hai-bo, LIU Liang，HUANG Yang-yang

(College of Mechanical Engineering, Northeast Dianli University, Jilin Jilin 132012, China)

Down time caused by CNC machining center failure is a main influence factor on its efficiency. In order to improve machining center and reduce maintenance time, origin 8 and matlab are used to draw, program, calculate and analyze its failure maintain time data. Firstly, machining center failure maintain time probability density function is drawn; Secondly, the distribution of its function is judged and parameter estimation is done; Finally, the CNC machining center failure maintain time according to lognormal distribution is proved. Measures to reduce CNC machining center maintain time is proposed combining function nature with failure data. It provides basis for machining center maintain.

CNC machining center; maintain time model; lognormal distribution

1001-2265(2014)05-0158-03

10.13462/j.cnki.mmtamt.2014.05.043

2013-02-01

张海波(1970—)，男，吉林省吉林市人，东北电力大学教授，博士，主要从事数控机床及数控系统可靠性研究等,(E-mail)zhhb@mail.nedu.edu.cn。

TH166;TG659

A