基于模糊参数逼近器的永磁同步电机反推控制
刘桂秋,潘德栋,李 龙
(沈阳工业大学 电气工程学院功率电子与电力传动研究所,沈阳 110870)
基于模糊参数逼近器的永磁同步电机反推控制
刘桂秋,潘德栋,李 龙
(沈阳工业大学 电气工程学院功率电子与电力传动研究所,沈阳 110870)
为了解决永磁同步电机的非线性、强耦合及不确定干扰等因素的影响,文章拟采用非线性动态逆控制和反推控制相结合的方法来设计控制系统。动态逆控制能够实现多输入多输出系统的精确线性化,解决电机多变量间的强耦合问题。反推控制能够保证系统全局一致渐近稳定,但对变化较快和较大的参数扰动抑制不够理想,在此基础上,采用模糊参数逼近器来消除负载扰动等因素对电机的影响。仿真结果证明了该方法的有效性。
反推控制;模糊参数逼近器;反馈线性化;永磁同步电机
0 引言
随着永磁磁性材料、半导体功率器件和控制理论的发展,永磁同步电机(PMSM)在中、小功率运动控制中发挥着重要作用。它具有体积小、功率因数高、转动惯量低等优点,从而工业生产过程中有着非常广泛的应用,如数控机床和工业检测过程中各种高精度的定位系统等。为了达到快速启动、加速和四象限运行,永磁同步电机控制方法主要是矢量控制,由于永磁同步电动机包含速度和电流的非线性耦合, 因此一般的线性控制方法效果不够理想。为了解决其控制问题,当前采用的非线性控制方法主要有模糊控制[1]、滑模变结构[2-3]、神经网络[4]和反推法[5]等。但这些非线性控制的设计方法比较复杂, 不易理解。
为此,本文提出一种新型控制器,将动态逆和反推控制结合起来,可实现对定子电流和转速同时控制,并设计模糊参数逼近器给出定子电阻、负载转矩和粘性摩擦系数的自适应律,使其快速逼近真实值,用以消除其系统稳定性的影响。仿真结果表明,设计的控制系统能够实现对电流和转速的快速跟踪,具有良好的稳定性。
1 永磁同步电机的数学模型
基于面装式的永磁同步电机,其基于同步旋转转子坐标的d-q模型[6]如下:(假定交轴、直轴电感近似相等,即Ld=Lq=L)
(1)
式中:id和iq为d,q轴定子电流;ud和uq为d,q轴定子电压;R为定子电阻;L为定子电感;P为极对数;J为转动惯量;B为粘性摩擦系数;TL为负载转矩;ω为转子机械角速度;ψf为永磁磁通。
设该方程的状态变量为:
输出变量为:
输入变量
得到非线性系统如下:
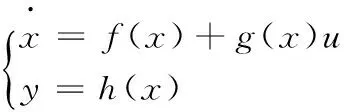
(2)
其中
2系统控制设计
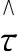

图1 PMSM控制系统结构框图
2.1 反推控制器设计
在利用反推法设计控制器时,需要先分别对给定ω、id求导r1、r2次,直至输入量uc=(τx,τy)T中的某一分量出现在微分式子中,从而得到相对阶,并产生输入与输出一对一的表达式。
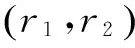
a)对所有的x0邻域内的x和所有1≤j≤2,1≤i≤2,0≤k≤ri-1,满足:
(3)
b)在x=x0处,下面的3×3阶矩阵是非奇异的:
(4)
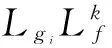
利用定义1,可以得到永磁同步电机数学模型的相对阶为r1=2,r2=1,于是可以得到
(5)
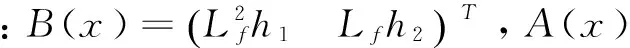
uc=A-1(S-B)
(6)
下面利用反推法求解S。反推法是一种由前往后递推的设计方法,从离控制输入量最远的方程入手,通过逐步修正算法设计镇定控制器,实现系统的全局调节或跟踪。在每一步把状态坐标的变化,不确定参数的自适应调节函数和一个已知李雅普诺夫函数的虚拟控制系统的镇定函数联系起来[8-9]。

(7)
对式(7)的每一步进行状态坐标的变化,使得式(7)和一个一致李雅普诺夫函数的虚拟控制系统联系起来,期望通过虚拟控制的作用,使得Xωi与虚拟反馈τωi具有某种渐近特性,从而实现整个系统的渐近镇定[12]。故定义误差变量
(8)
其中,τω1为待定虚拟控制量,虚拟控制本质上是一种静态补偿思想,前面子系统必须通过后边子系统的虚拟控制才能达到镇定目的。在每一步构造一个李雅普诺夫函数,使每一状态分量具有适当的渐近特性。式(8)本质上是一个微分同胚,因此为镇定原系统,只需要镇定原系统状态与虚拟反馈τω1间的误差Zω即可。
对Zω1求导得
(9)
其中Cω1>0。对于Zω1定义李雅普诺夫函数
(10)
求导,得
(11)
令τω1=-Cω1Zω1,则有
(12)
对Zω2求导,得
(13)
其中,
对Zω1、Zω2定义李雅普诺夫函数
(14)
求导,得
(15)

可见误差是渐近收敛的。
由式(13)得
(16)
定义e=id-id_c,其中id_c为给定电流信号。对于id控制,由于相对阶r2=1,故可取为
(17)
将(16)、(17)带入(6)式,即可求出控制量。
2.2 模糊参数逼近器设计
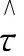

(16)
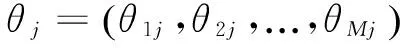
(18)
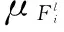
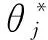
(19)
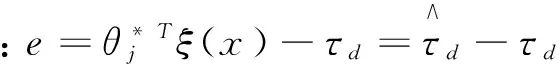
(20)
下面一般采用梯度下降法调整θj,此处借鉴文献[12]的方法:
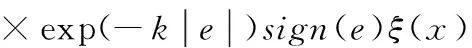
(21)

3 仿真结果与分析
为验证所采取方法的有效性,对永磁同步电机控制系统的跟踪性能进行了仿真研究。
永磁同步电机的参数选择为:
B=0.0003,R=0.958,
L=0.00525,J=0.000632,
ψf=0.182,P=4。
控制器的参数选择为:
Cω1=300,Cω2=200。
模糊参数逼近器的参数选择为:
η1=100,η2=200,
k1=0.02,q=5,p=9。
在[-1,1]上定义5个集合分别为NB、NS、ZE、PS、PB,相应的隶属度函数选择为:

μNS=exp(-(x1+0.25)2),

μNS=exp(-(x1-0.25)2),

初始给定电流id和转速ω分别为1mA和5 r/min。
其中图2为电机转速跟踪性仿真图,在0.4s时改变给定转速为10 r/min;图3为电机电流跟踪性仿真图,在0.5s时改变给定电流为2mA;图4为电机负载转矩仿真图,在0.6s时由负载由空载突变到1N·m;图5为电机定子电阻仿真图。在0.7s时定子电阻提高10%;图6为电机粘性摩擦系数仿真图,在0.8s时定子粘性摩擦系数提高10%。

图2 电机转速
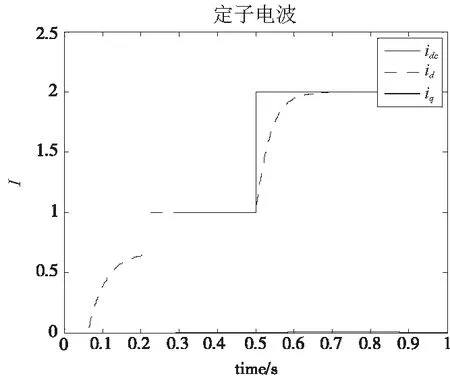
图3 电机电流
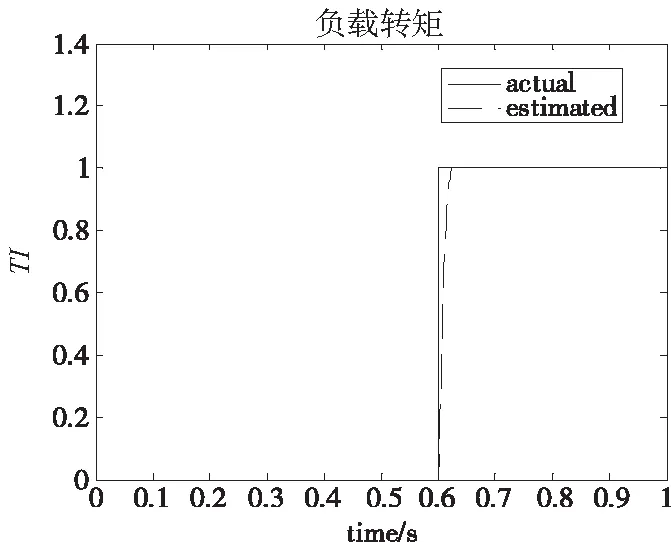
图4 负载转矩
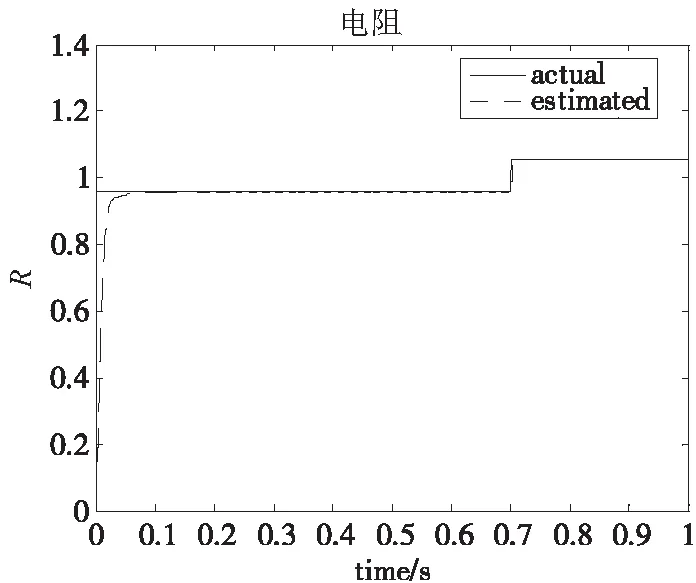
图5 电阻
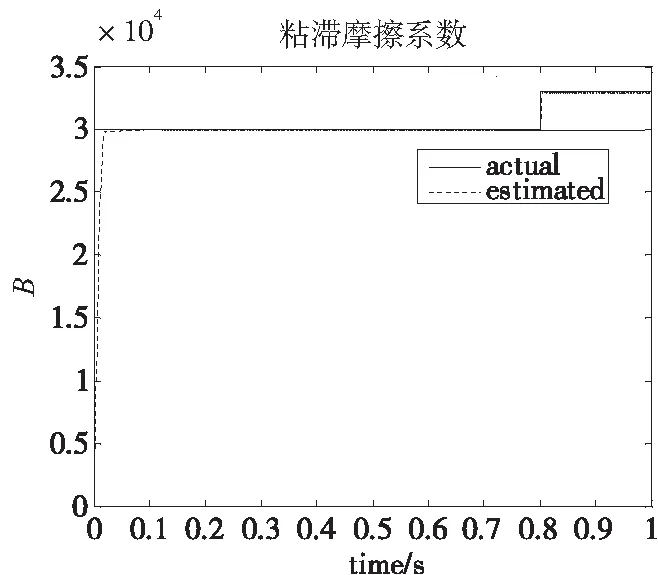
图6 粘性摩擦系数
从仿真结果可以看出,所采用的控制方法能够快速跟踪给定电流和转速,并且在突加负载扰动时,参数逼近器可以快速逼近负载扰动、定子电阻和粘性摩擦系数的真实值,从而提高系统的跟踪精度。
4 结论
本文所设计的基于动态逆反推控制的永磁同步电
机模糊参数逼近器调速系统,在反推控制中加入了动态逆控制,实现定子电流和转速的解耦,并作为调速系统的输入,结合模糊参数逼近器消除负载转矩、定子电阻和粘性摩擦系数扰动对系统稳定性的影响,并且通过Lyapunov定理证明了所设计的控制器的稳定性。在给定定子电流和转速变化时,仿真结果表明所设计的控制系统实现了对给定定子电流和转速的快速跟踪性,具有较高的跟踪精度。
[1] Han Ho Choi. Design and Implementation of a Takagi-Sugeno Fuzzy Speed Regulator for a Permanent Magnet Synchronous Motor[J]. IEEE Transactions on Industry Electronics, 2012, 59(8):3069-3077.
[2] 王宪,杨坤等.新型模糊滑模控制器在交流位置伺服系统中的应用研究[J].计算机应用研究,2011,28(1):65-68.
[3] 童克文,张兴等. 基于新型趋近律的永磁同步电动机滑模变结构控制[J].中国电机工程学报,2008,28(21):101-106.
[4] 李毓洲,阳 林.基于小波神经网络的永磁同步电机无速度传感器滑模控制[J].电机与控制应用,2010,37(3):31-34.
[5] Chih-Hong Lin, Ren-Cheng Wu. Adaptive Recurrent Network Network Uncertainty ObserverBased Integral Backstepping Control for a PMSM Drive System [J]. International Journal of Power Electronics and Drive System, 2012, 2(2): 127-137.
[6] Pragasen Pillay, Krishnan R. Modeling of permanent magnet motor drives[J]. IEEE Transactions on Industry Electronics, 1988, 35(4): 537-541.
[7] Alberto Isidori著,王奔,庄圣贤译. 非线性控制系统[M].北京:电子工业出版社,2005.
[8] 胡跃明.非线性控制系统理论与应用[M].北京: 国防工业出版社,2002.
[9] Farell J, Sharma M, Polycarpou M. Backstepping based flight control with adaptive function approximation[J]. J. of Guidance, Control and Dynamics, 2005, 28(6): 1089-1102.
[10] Wang L X, Mendel J M. Back-propagation fuzzy systems as nonlinear dynamic system identifiers[A]. IEEE International Conference on Fuzzy Systems[C]. 1992, 3: 1409-1418.
[11] Yue S H, Zhang K C. An optimal fuzzy approximator [J]. Appl. Math.J. Chinese Univ. Ser. B, 2002, 17(2): 236-240.
[12] Yunfeng Liu, Fei Cao, et al. A Novel fuzzy approximator with fast terminal sliding mode and its application[J]. Fuzzy Systems and Knowledge Discovery, Lecture Notes in Artificial Intelligence, 2006,Vol.4223: 179-187.
(编辑 李秀敏)
The Backstepping Control of PMSM Based on Fuzzy Parameter Approximation
LIU Gui-qiu,PAN De-dong,LI Long
(Institute of Power Electronics and Motion Control, School of Electrical Engineering, Shenyang University of Technology, Shenyang 110870, China)
In order to solve the influence of the permanent magnet synchronous motor nonlinear, strong coupling and uncertain disturbance, this paper is intended to apply the method of combing the nonlinear dynamic inversion control and backstepping control to design the control system. The MIMO strongly coupled system is accurately linearized using the dynamic inversion technique which can solve the problem of the motor's multivariate and strong coupling. The backstepping control law guarantees the system global stability, but it can not attenuate the effects well for the changing faster and larger parameters. On the basis, the fuzzy parameter approximation based on fuzzy basis function vector is used to eliminate the effect of the disturbance. The efficiency of the proposed control scheme is verified using computer simulation.
backstepping; fuzzy parameter approximation; feedback linearization; PMSM
1001-2265(2014)05-0117-04
10.13462/j.cnki.mmtamt.2014.05.030
2013-09-10;
2014-02-18
刘桂秋(1962—),女,沈阳人,沈阳工业大学副教授,研究领域为电力电子电机及其控制系统,(E-mail)Liugq_shy@sina.com; 通讯作者:潘德栋(1988—),男,沈阳人,沈阳工业大学硕士研究生,研究方向为交流伺服系统控制理论与应用,(E-mail)dedong001@163.com。
TH166;TG65
A

