航空领域国产加工中心速度谱的研究*

方 杰，马宇鹏，陈 菲，刘 畅，蒋敬仁，段 炜，周传阳

(吉林大学 机械工业数控装备可靠性技术重点实验室，长春 130025)

航空领域国产加工中心速度谱的研究*

方 杰，马宇鹏，陈 菲，刘 畅，蒋敬仁，段 炜，周传阳

(吉林大学 机械工业数控装备可靠性技术重点实验室，长春 130025)

为了初步建立航空领域国产加工中心速度谱及其分布模型，对航空领域若干生产企业所使用的7台国产加工中心进行了平均每台1974小时的现场连续跟踪记录，对采集到的加工中心的运行情况、加工零件数目、切削参数、零件每一工步的加工时间等数据进行统计和分析，初步建立了航空领域国产加工中心速度谱，并提出了运用模拟退火优化方法对速度谱的概率密度以及累积分布的数学模型进行参数估计及优化，通过Matlab软件对所建立的模型进行拟合及残差分析，得到了较好的拟合效果。

加工中心；速度谱；可靠性试验；模拟退火优化

0 引言

在数控机床可靠性分析，特别是可靠性设计中，数控机床载荷不仅是必不可少的已知条件，而且其是否准确、可靠是可靠性设计成败的关键之一[1]。同时，数控机床载荷谱也是进行数控机床可靠性试验设计的重要依据。因此，机床载荷谱的研究就显得十分必要。

载荷谱是结构或机器零部件所承受的随时间连续变化的载荷，也称作“载荷-时间历程”或“应力-时间历程”[2-3],这里所说的载荷可以是力、力矩、功率、速度等[4]。我国在航空、汽车、农业机械、重型机械等诸多领域都相继进行了载荷谱的研究[5-8]。前苏联专家烈歇托夫[9]在二十世纪五十年代提出了普通机床的载荷谱，该载荷谱在机床传统设计中长期沿用。在数控机床载荷谱研究方面，王义强[1]等通过收集数控车床典型用户企业在零件加工过程中的切削参数、切削条件和零件图、加工工艺卡、车床基本信息等数据，采用多元回归分析方法建立了数控车床载荷谱分布模型。黄祖广[10]等通过对加工中心的切削数据的调研、收集和处理，分别建立了国产加工中心铣削、钻削、镗削等典型加工工艺的功率谱和速度谱。加工中心速度谱为其主轴转速与其所对应的相对运转时间的分布规律，速度谱为载荷谱的重要组成部分。速度谱不仅是加工中心及其关键功能部件设计与可靠性试验设计的重要依据，而且，加工中心用户企业可以依据速度谱更加合理的安排生产与维护设备。另外，速度谱也是加工中心及其关键功能部件进行可靠性试验设计的重要依据。本文在“高档数控机床与基础制造装备”国家重大科技专项的支持下，依据航空领域国产加工中心可靠性设计和可靠性试验的需求,对航空领域某企业的7台国产加工中心进行现场跟踪，记录加工中心的运行情况、加工零件的数量、切削参数以及加工每一个零件的加工时间等数据，对切削数据进行了分析与处理，分别对加工中心铣削、钻削和镗削等典型加工艺进行分析与研究，并对加工中心速度谱及速度谱分布模型的建立方法进行了探讨。最终采用模拟退火优化方法对贝塔分布、伽玛分布、威布尔分布、对数正态分布这四种模型进行了参数估计及优化，通过柯尔莫戈洛夫拟合优度检验对比，确定对数正态分布为本文采样数据的最优分布模型。

1 数据的采集与预处理

1.1 数据的采集

为了科学的建立航空领域国产加工中心的速度谱，对航空领域若干企业所使用的7台国产加工中心进行了平均每台1974小时的现场跟踪，所采集的数据包括这些企业生产的航空发动机的机匣、叶片、转子等典型的零件的数目、切削参数、加工每一个零件所消耗的时间等数据以及加工中心的运行情况。利用这些数据建立航空加工中心切削数据库，为建立速度谱及其分布模型提供依据。

1.2 数据的预处理

根据采集到的7台加工中心每台加工每种零件的数量以及加工零件所对应的每一工步的切削速度、切削时间等工艺参数，计算7台加工中心的总考核时间TΣ和总切削时间T切削，得出加工中心切削率η切削为：

(1)

由(1)式可知，航空领域国产加工中心的切削率较高，即设备的运行效率较高，这是因为大部分航空零件材料硬度高，切削难度大，切削用量和进给量小，零件加工速度慢，切削时间相对辅助时间较长。

2 速度谱的建立

为了便于数据的处理和分析，通过对计算数据的观察与分析，引入主轴相对转速(nr)这一概念，nr是指加工中心的主轴速度ni与最高速度nmax之比。其数学表达式为:

(2)

根据机床低速、中速和高速的定义，并综合考虑机床设计的最高速度，对所分析的加工中心速度作相对于该机床最高速度而言的低速、中速和高速分类处理。对主轴相对转速nr进行如表1分类处理：

表1 主轴相对转速nr分类

最后，根据航空领域国产加工中心的主轴相对转速nr，统计不运转、低速、中速和高速四类速度所占的时间比例图，即航空领域国产加工中心的速度谱，如图1所示。

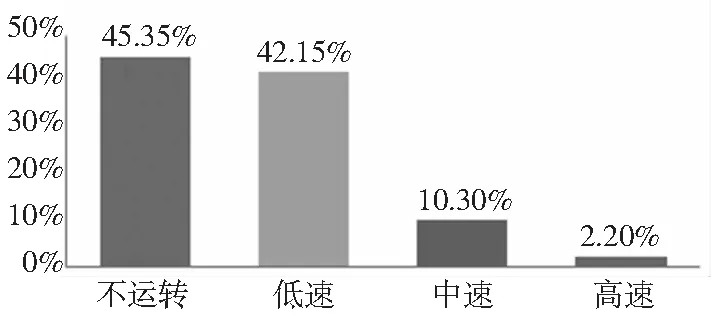
图1 航空领域国产加工中心的转速分布图

图1分析结果可以作为航空领域国产加工中心及其关键功能部件主轴的可靠性试验的重要依据。同时，从得到的速度谱可以看出，航空领域国产加工中心不运转和低速情况所占的比例较大，中速和高速所占的比例较小。这反应出大部分航空领域零件加工低切削速度、慢进给的特点，这是由零件硬度高，加工难度大造成的。

传统的寿命试验，往往试验时间长，试验难度大，因此可靠性试验一般采用加速寿命试验。加速寿命试验要求利用与物理失效规律相关的统计模型对在超出正常应力超出正常应力水平的加速环境下进行试验[11]。本文依据疲劳损伤累计原理，采用强化中载和重载所占的比例，减小低速和不运转的比例的方式对航空领域加工中心主轴进行加速试验。具体的可靠性加速寿命试验时间分配方案如表2所示。

表2 航空领域可靠性加速寿命试验时间分配表

3 速度谱分布模型的建立

为了建立航空领域国产加工中心速度谱的分布模型，我们对采集到的加工中心的主轴速度分组，将分组后的主轴速度与其对应的相对运转时间的分布规律进行分析研究。将各组主轴速度所对应的运行时间ti除以总切削时间T切削得到主轴的各组速度所对应的频率(ωi)

(3)

再计算相对转速概率密度采样值，通过下式获得：

(4)

这里，Δnr—主轴相对转速的组距。

综合式(3)和式(4)，得到主轴相对转速nr和主轴相对转速概率密度估计值f(nr)的数据。通过对航空领域国产加工中心的现场跟踪采集得到的大量数据经分析得到主轴相对转速nr、主轴相对转速概率密度采样值f(nr)和主轴相对转速分布函数采样值F(nr)的统计数据如表3。

经过上述处理就得到了航空领域主轴的主轴相对转速及其对应的概率密度的数据，即航空领域国产加工中心速度谱的采样数据。根据对采样数据的初步分析，我们从常用的几种统计分布中初选贝塔分布、伽玛分布、威布尔分布、对数正态分布四种基本符合上述情况的候选分布模型进行参数估计。对于威布尔分布的累积分布函数模型以及对数正态分布、贝塔分布、伽马分布的概率密度函数模型这四种不含有积分项的模型，本文采用多元线性回归分析方法进行了模型参数估计并进行线性假设的显著性检验，再利用柯尔莫戈洛夫检验方法进行拟合优度检验，以确定最佳的拟合模型。具体计算过程如下：

假设随机变量y和x1，x2，(，xp是线性关系，第i次采样数据为(yi；xi1，xi2，(，xip) ，(i=1，2，(，N)，则可得到下列方程：

yi=b0+b1xi1+b2xi2...+bpxip+εi

(5)

这里，误差项εi服从正态分布N(0,σ2)，且εi互相独立 (i=1，2，(，N)； (b0，b1，(，bp)是未知参数；

为了便于表达和计算， 我们引入如下矩阵，记

B=(b0b1b2...bp)T

Y=(y1y2...yN)T

E=(ε1ε2…εp)T

则方程(5)可表示为矩阵形式：

Y=X·B+E

(6)

称X为结构矩阵，B为参数矩阵，E为误差矩阵。

构造矩阵：

则正规方程组的矩阵形式为

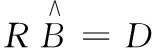
(7)

这里R是x1，x2，...，xp的互相关系数矩阵。

我们可得到模型(5)的最小二乘估计参数

(8)

这里，C=(cij)=R-1，R-1是R的逆矩阵；上角标-1表示矩阵的转置。

(9)

其中，n—数据总频数；

m—多元线性规划正规方程组未知量个数；

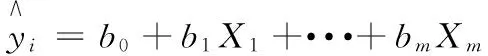
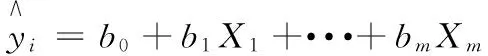
yi=Yi；

如果F≥Fα(n-m-1),则认为在显著性水平α下，Y与X1,X2,···,Xm成线性关系。

另外，对于探求采样数据究竟服从何种分布模型，还需进行拟合优度检验，本文采用柯尔莫戈洛夫检验(Dn检验)法进行拟合优度检验。Dn检验法的统计量D可由下式计算：

(10)

其中，Fn(x) — 经验分布的累积分布函数；

Fo(x) — 假设分布的累积分布函数；

xi— 第i个样本值；

n— 样本容量。

如果D≤Dα(n),则认为在显著性水平α下， 该批数据服从分布Fn(x)。

以对数正态分布为例，其概率密度函数模型为：

(11)

上式两边取对数，并整理：

(12)

令

(13)

式(13)代入式(12)中，得到如式(5)的二元回归方程。由式(13)得：

(14)

利用Matlab对上述过程进行处理，求得：

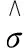
同样，对威布尔分布、贝塔分布和伽马分布这三种模型进行参数估计，然后对四种分布模型分别进行线性假设显著性检验以及拟合优度检验，其结果见表4。

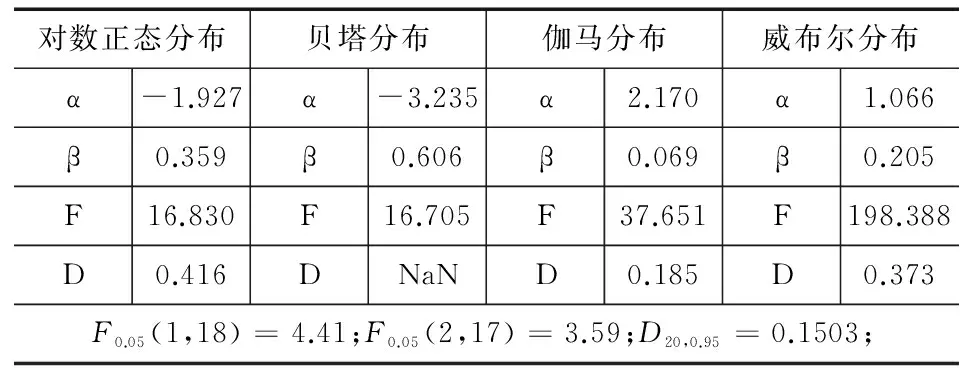
表4 分布参数估计(线性回归分析)

通过上表可以看出，虽然所选取的四种分布模型的F值均大于F0.05，但是他们的柯尔莫戈洛夫检验统计量D20均大于D20,0.95，因此应该拒绝原分布假设。产生这种现象的原因在于在对各个分布模型进行线性化的过程中，模型的非线性关系被改变，导致线性回归后数据的残差分布不具有正态性和独立性，导致参数估计出现较大误差。

针对这样的问题，本文以采样数据经验分布与拟合分布的残差ε为输入条件，采用模拟退火优化方法对各个分布的参数进行估计。

所采用的优化变量为：

ε=norm(Ffit(xi)-F(xi))

(15)

其中：Ffit(xi)—拟合分布的累积分布概率；

F(xi)—相对转速的经验分布频率；

利用Matlab编写模拟退火优化方法程序，得出各个分布的参数估计值，并对各个分布进行柯尔莫戈洛夫检验，结果见表5。图2～图5分别为各个分布的概率密度和概率累计分布在模拟退火优化后的拟合图。

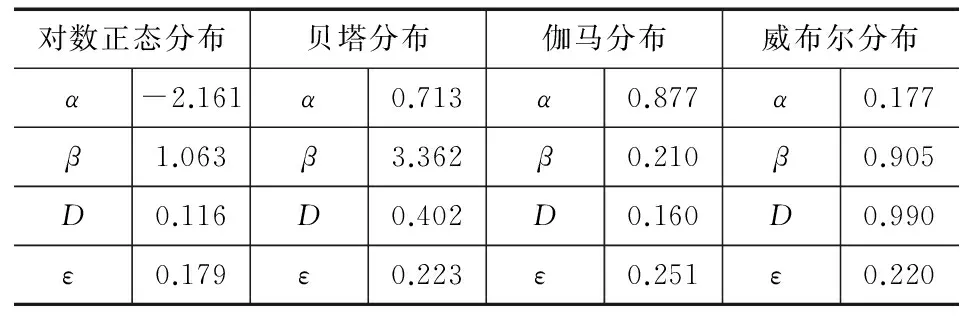
表5 分布参数估计(模拟退火优化)

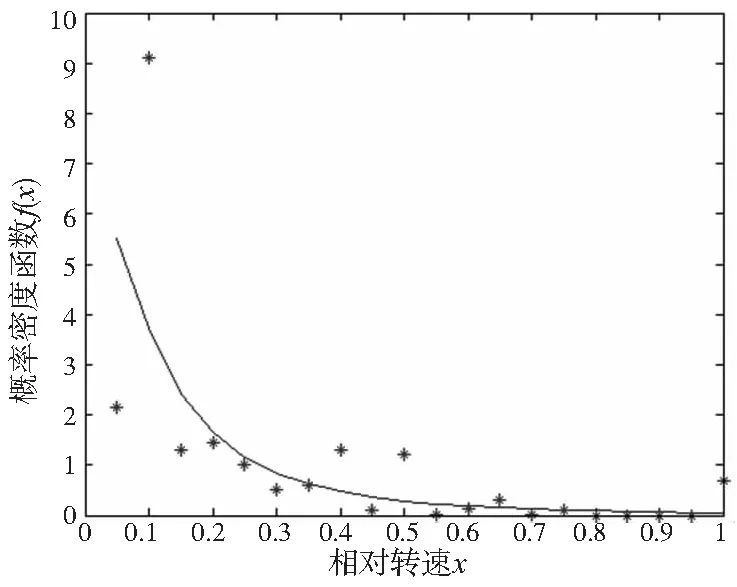
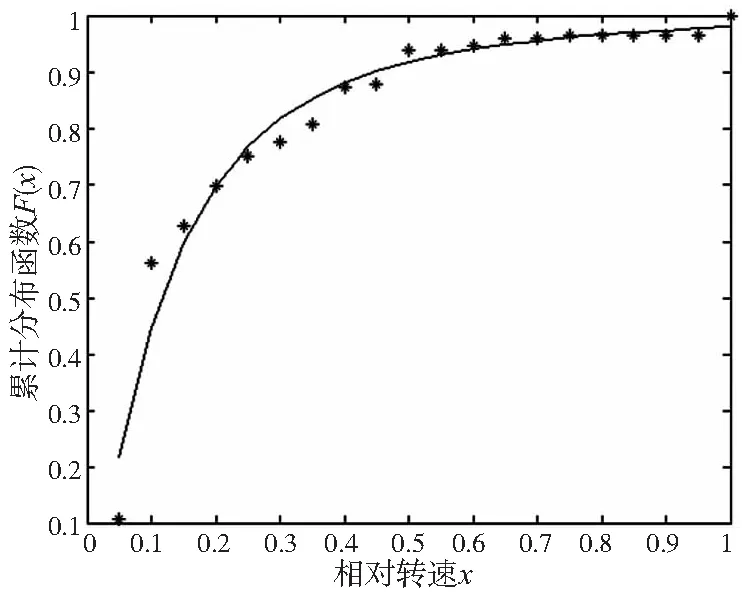
图2 对数正态分布拟合曲线(模拟退火优化)

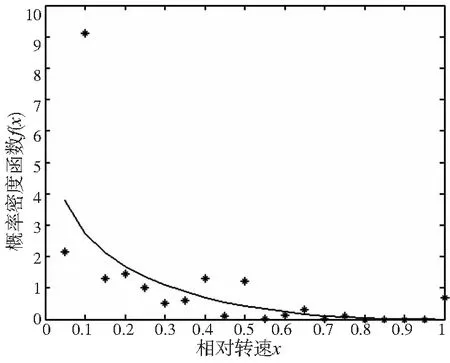
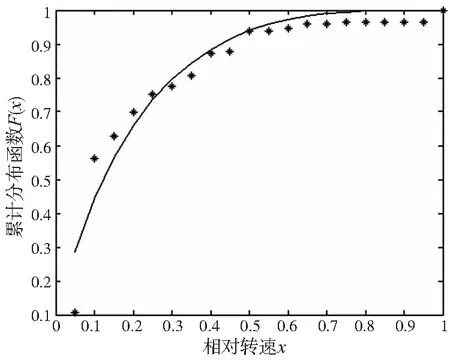
图3 贝塔分布拟合曲线(模拟退火优化)

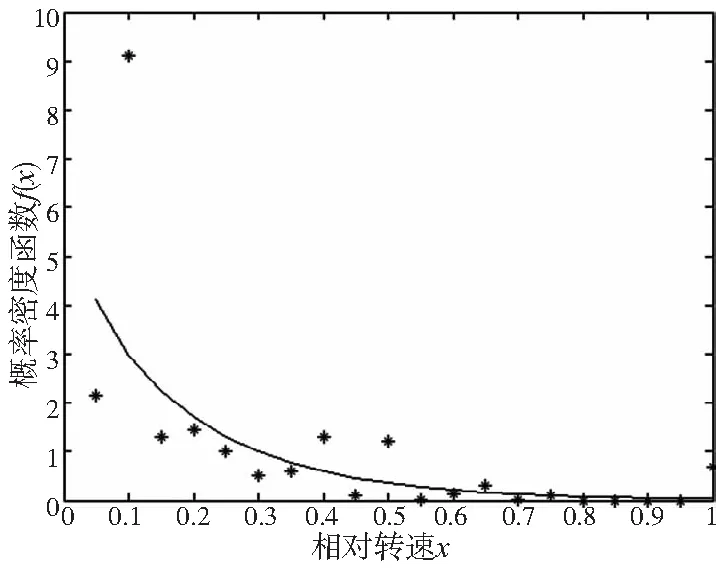
图4 伽马分布拟合曲线(模拟退火优化)

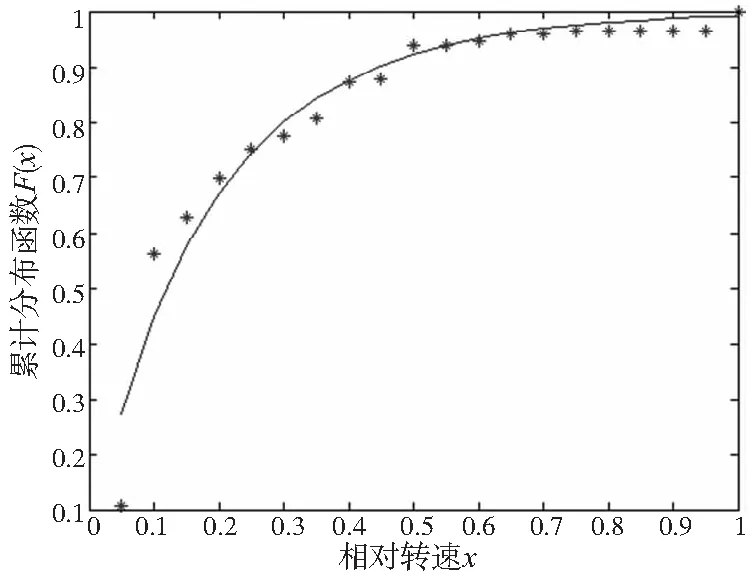
图5 威布尔分布拟合曲线(模拟退火优化)

查表可以得到D20,0.95=0.1503，对比表5中的结果可以看出，只有对数正态分布通过了柯尔莫戈洛夫检验，同时对比图2—图5的拟合效果图也可以看出对数正态分布的拟合效果较好，且残差ε值为0.179亦为最小。因此参数为μ=-2.161，σ=1.063的对数正态分布为本文采样数据的最优分布模型。该批航空领域国产加工中心速度谱为：

4 结束语

本文通过到航空加工中心典型用户驻厂现场采集和收集加工中心的运行情况、加工零件数目、切削参数等数据，并在对航空领域若干企业的7台国产加工中心进行平均每台1974小时的现场连续跟踪的基础上，对采集和收集的数据进行统计和处理，统计出了航空领域国产加工中心铣削、钻削和镗削的加工时间分布情况。通过对各加工速度及其对应的加工时间的分析，初步建立了航空领域国产加工中心速度谱，为加工中心的可靠性试验提供了一定的依据。同时，分析了主轴相对转速及其对应的概率密度和分布函数，分别采用多元线性回归分析方法和模拟退火优化方法对贝塔分布、伽玛分布、威布尔分布、对数正态分布这四种模型进行了参数估计及优化，通过线性假设的显著性检验和柯尔莫戈洛夫拟合优度检验，最终确定对数正态分布为本文采样数据的最优分布模型，同时确定了航空领域国产加工中心主轴相对转速符合采样数据的概率密度和分布函数的表达式。

加工中心载荷谱的建立是一项长期而艰巨的工作，需要耗费大量的人力、物力和财力，采集的数据越多，所建立的载荷谱价值越高。本文所提出的速度谱的建谱方法和分布模型的建模过程为加工中心的其他载荷谱如切削力谱、功率谱的建立提供了一种参考。由于条件的限制，本文所建立的加工中心速度谱仍需要不断补充和完善。

[1]王义强,贾亚洲,于骏一，等.数控车床载荷谱数据库的建立[J].吉林工业大学学报，1998(1)：34-38.

[2]高镇同,熊俊江.疲劳可靠性[M].北京：北京航空航天大学出版社,2000.

[3]徐灏.概率疲劳[M]，沈阳：东北大学出版社，1994.

[4]王义强.计算机数控车床可靠性分析与设计方法的研究[D].长春：吉林大学,1999.

[5]宋迎东，高德平.发动机机动飞行类综合载荷谱研究[J].航空动力学报，2002，17(2): 212-216.

[6]刘庆华，张为公.基于车轮力传感器的道路载荷谱采集系统设计[J].江苏大学学报(自然科学版)，2011,32(4):389-393.

[7]张英爽，王国强，王继新，等.工程车辆传动系载荷谱编制方法[J].农业工程学报，2011，27(4):179-183.

[8]谭援强，左晃，张跃春，等.多级多工况传动载荷处理方法及研究[J].机械强度，2011，33(6):932-938.

[9]Л . H .烈歇托夫.机床零件的计算,郑明译[M], 北京：商务印书馆，1956.07.

[10] 黄祖广，赵钦志，盛伯浩，等.加工中心可靠性试验载谱的研究.制造技术与机床，2008(2)：60-64.

[11] YurkowskyW,SchafterRE,FinkelsteinJM.Acceleratedtestingtechnology.TechnicalReportNO.RADC-TR-67-420,1967: 1-2.

[12] 高文森，潘伟.大学数学-随机数学[M]，北京：高等教育出版社，2004.

(编辑 李秀敏)

Research on the Velocity Spectrum of Domestic-made Machining Centers Applied in The Aviation Domain

FANG Jie,MA Yu-peng,CHEN Fei,LIU Chang,JIANG Jing-ren,DUAN Wei,ZHOU Chuan-yang

(Key Laboratory of CNC Equipment Reliability Technique of Machinery Industry,Jilin University,Changchun 130025,China)

Based on the operating condition, number of parts machined and cutting parameters gathered and collected via continuously on-site tracing of 7 machining centers for 1974 hours each, this paper has formatted the mathematical model, including the probability density function and the cumulative distribution function of the velocity spectrum of domestic-made machining centers used in aircraft manufacturing factories by mean of data processing and statistics with the Simulated Annealing Method under Matlab, gaining the estimated parameters and residual errors of each chosen distribution model. The fitting result turned out to be relatively good.

machining centers, velocity spectrum, reliability test, simulated annealing method

1001-2265(2014)05-0035-05

10.13462/j.cnki.mmtamt.2014.05.009

2013-08-28;

2014-01-16

国家科技重大专项:千台国产加工中心可靠性提升工程(2013ZX04011-012)

方杰(1988—)，男，四川眉山人，吉林大学硕士研究生，研究方向为数控装备可靠性，(E-mail)fonjet@qq.com; 通讯作者:马宇鹏(1988—)，男，吉林松原人，吉林大学硕士研究生，研究方向为数控车床载荷谱编制方法，(E-mail)michael.joseph.ma@hotmail.com。

TH113;TG65

A