基于零空间追踪算法的铣削功率信号分析*

李衍佳，石新华，邵 华

(上海交通大学 机械与动力工程学院，上海 200240)

基于零空间追踪算法的铣削功率信号分析*

李衍佳，石新华，邵 华

(上海交通大学 机械与动力工程学院，上海 200240)

功率信号因获取简便、成本低等特点被广泛应用在切削过程监控中，因此对功率信号的特征进行深入分析非常必要。利用零空间追踪算法(Null Space Pursuit，NSP)分解铣削功率信号，分析分量及其能量分布的特征；通过计算能量分布与相关系数的相关程度，探究NSP的自适应性。分析结果表明，铣削功率信号的NSP分量包含大量有关铣削过程的信息，分量能量集中在前4阶；铣削参数恒定时，功率信号可分为静态分量和动态分量两部分；NSP分解铣削功率信号的自适应性良好。

铣削；功率信号；零空间追踪；NSP

0 引言

与其它电量参数(电流、功率因数等)相比，功率信号具有灵敏度高、受干扰小的优点，且其获取简便，测量装置成本低廉、安装无需改装机床，被广泛应用在切削过程监控中。邵华等[1]在小波变换和独立分量分析的基础上提出了一种单通道盲源分离算法，运用该算法分离铣削功率信号得到了能用于监控铣刀和主轴状态的多种源信号；Faleh A[2]等提出监测功率消耗微分的方法，该方法仅记录实际钻削过程的功率，不记录驱动主轴电机和进给电机所需功率，试验表明该方法的监测刀具磨损效果优于传统功率监控方法；王海丽[3]等建立了机床主电机功率信号的自回归时序模型，并把其作为神经网络的输入之一，试验表明该方法具有较好的刀具破损识别效果。然而，大量研究表明，目前提出的绝大部分功率监测方法适应性不强，大多局限于特定的加工设备或加工参数。因此，对机床功率信号的特征进行深入分析有极为重要的现实意义。本文以铣床功率信号为研究对象，以期对其他机床功率信号的研究提供一定的借鉴。

近年来，信号处理方法发展迅速，从傅立叶变换到短时傅立叶变换、Gabor变换，再到小波变换，研究人员把目光从全局分析转移到局部分析，从单分辨率拓展到多分辨率。但这些方法对非平稳信号的分析效果并不理想，因为其基本时域信号都是平稳的简谐信号，是全局性的信号。直到1996年，Norden E.Huang等提出基于瞬时频率的EMD算法，完全适用于非平稳信号的方法才真正出现。2010年，彭思龙等[4]提出的零空间追踪算法同样适用于非平稳信号，与EMD有一定的类似，其分量局部窄带信号比EMD的分量IMF更易理解。

1 零空间追踪算法

零空间追踪算法(Null Space Pursuit，NSP)，是一种基于算子的信号分解算法，由彭思龙等于2010年提出。基于算子的信号分解算法同样由彭思龙等人提出，其主要目的是将信号分解为一系列局部窄带信号分量的叠加，其思想及算法步骤等介绍如下。

1.1 算子的信号分解算法

基于算子的信号分解算法[5]的思路是，将一个紧支撑的奇异的局部线性算子作用在信号上，由于算子是奇异的，这样得到的信号与原信号相比必然有一部分“消失了”。根据局部窄带信号的定义(见下文)可以知道，这部分“消失了”的信号正是局部窄带信号，并且这部分信号属于算子的零空间。所以，只要能从信号中自适应的获得算子的参数，就能从信号中分离出“消失了”的信号——局部窄带信号，从而实现信号分解。

1.1.1 局部窄带信号

窄带信号可以用A(t)cos(ωt+φt))(这里A(t)的最大频率远小于ω，φ(t)的变化很缓慢)来描述。将窄带信号的定义拓展，如果某信号在任意时间处存在一个邻域使得该邻域的信号可被近似看成是窄带信号，那么该信号被称之为局部窄带信号[5]。

彭思龙等人根据局部线性算子来定义局部窄带信号，同时定义了两种局部线性算子：积分式(1)和微分算子式(2)。

T(S)(t)=ʃBtS(x)dx

(1)

(2)

根据两种局部线性算子定义了两类局部窄带信号：

对于局部窄带信号S(t)，如果存在奇异的积分算子T和整数n使得下式成立，则称S(t)为第一类局部窄带信号。

Tn(S)(t)=0(n≥1)

(3)

对于任意t处的局部窄带信号S(t)，存在序列α∈l2(Z)使得A(x)=Σk∈Zα(k)xk的零点均为虚数，且

Tα(S)(t)=0

(4)

则称S(t)为第二类局部窄带信号。

1.1.2 基于算子的信号分解

基于算子的信号分解算法主要解决式(5)的问题，式中S(t)为某信号，S1(t)是第一类或第二类局部窄带信号，U(t)是残余信号。

S(t)=S1(t)+U(t)

(5)

由于S1(t)是局部窄带信号，所以存在一个奇异线性算子T使得T(S1)(t)=0。解决以下优化问题就能获得U(t)，实现信号分解。

(6)

1.2 零空间追踪算法

零空间追踪算法的优化方程如下：

argmin{‖TS(S-U)‖2+λ1(‖U‖2+γ‖S-U‖2)+F(Ts)}

(7)

式中γ是泄露参数，最后一项是算子Ts的拉格朗日项。γ是泄露参数，因为γ的值决定了S-U的信息量大小，控制了算法的“贪婪”程度。

2 铣削功率信号的NSP分量分析

2.1 仿真信号分析

为了了解零空间追踪算法的性能，先用它来分解仿真信号S=0.3sin(4t) +sin(10t)+t+10，λ1，∈的初始值依次取为1×10-8，1×10-7分解结果如图1所示。

图1 零空间追踪分解仿真信号

图1中，S是仿真信号，U1、U2、U3分别是零空间追踪的1、2、3阶分量。仔细观察图1不难发现，U1是信号S的趋势项，对应于分量t+10；U2、U3分别对应于S中的分量sin(10t)和0.3sin(4t) 。从图中可知，除在端点处有一定的波动外，U1、U2无论是频率还是幅值都能很好的逼近原信号分量；U3的频率十分逼近原信号分量，幅值则有一定差别。

2.2 铣削功率信号分析

图2是铣削功率信号的零空间追踪分解分量及其功率谱。试验条件如下：工件材料为45号钢，切削深度ap=1mm, 主轴转速v=160r/min, 进给速度f=42mm/min，两个处于相对位置的铣片铣削(刀柄齿数为四)。λ1,∈的初始值依次取为1×10-4,1×10-7。

图2 铣削功率信号的零空间追踪分解 (左边的U1-U5是一到五阶分量，右边是对应的功率谱图)

图3 功率信号及零空间追踪分解(S为原功率信号)

从图2可知，第5阶分量U5的幅值比其他4阶分量小得多，说明第5阶分量在原功率信号中占的比重很低，故6阶及以上的分量不再列出。比较第1阶分量与其他4阶分量的时域图可以发现，第1阶分量的幅值远大于其他4阶分量，而且幅值变化幅度很小。这说明第1阶分量是功率信号的趋势项，是一个直流分量，该分量在原功率信号中占的比重极高，且在铣削参数恒定时其幅值基本恒定不变。这一点也可以从其功率谱图得到验证。这表明铣削参数恒定时，功率信号可分解为静态分量和动态分量两部分：静态分量(图3中U1)正是NSP分解的第1阶分量，该分量变化幅度很小；动态分量(图3中R1)则是呈周期性变化的，且动态分量中周期最大的分量是主轴转频分量。

从第2-5阶分量的功率谱可知，其频率依次是4.6Hz,9.2Hz,2.3Hz和13.8Hz。因为主轴转速v=160r/min，所以理论上主轴转频fv=160/60≈2.67Hz。由于试验所用铣床传动系统含带轮传动，而皮带与带轮间存在滑动，带轮传动无法保证严格的传动比，所以第4阶分量U4是包含主轴状态信息的主轴转频分量，这说明铣床实际的主轴转频约为2.3Hz。另一个值得注意的分量是U2，其幅值很大(仅小于直流分量)，其频率是主轴转频的二倍，应为处于相对位置的两铣片铣削所致，故分量U2是包含铣片位置信息的分量。另外，分量U4是频率为主轴转频四倍的分量。由以上分析知，功率信号的NSP分量包含丰富的有关主轴状态和刀具状态的信息，因此，如能很好的利用这些信息，铣削过程监控将变得简便。

3 铣削功率信号能量分布特征分析

3.1 铣削功率信号能量的表征

类似EMD的IMF分量能量分布[6]，建立铣削功率信号NSP分量的能量分布，具体步骤如下：

1)对铣削功率信号进行NSP分解，得到各分量Ui；

2)计算各分量的能量:

(8)

3)计算各分量的能量占总能量的比例ηi：

由2.2中的分析知，如果计算Ei与原功率信号总能量E的比值，E1/E的值将非常大(数据证明均大于99.9%)，这不利于对2阶及以上分量的能量分布进行分析，而大多时候研究人员关心的正是这些动态分量。因此，这里将功率信号的总能量值换成去除第1阶分量后信号的总能量值Er。

(9)

3.2 功率信号采集

试验分三组，记为试验一、二、三，采集到的功率信号依次记为Y1、Y2、Y3。三组试验铣削参数相同：切削深度ap=1mm,主轴转速v=160r/min,进给速度f=42mm/min，工件材料均为45号钢，刀柄齿数为四。试验一为单一铣片铣削，试验二为两相对位置铣片铣削，试验三为三铣片铣削。

信号采集的采样频率为2000Hz。为去除高频干扰，对信号Y1、Y2、Y3进行100点滑动平均处理，处理后的信号依次记为S1、S2、S3。

3.3 NSP分量能量特征分析

3.3.1 NSP分解

对信号S1、S2、S3依次进行NSP分解，均选取前7阶分量进行进一步分析，对S1的分解结果见图4。

根据[7]，EMD分解的第1阶IMF分量频率最高，随着分解的进行IMF频率越来越低。而NSP的分解结果则恰好相反(图4)，第1阶分量是趋势项，随着分解的进行分量的频率有逐步增大的趋势。

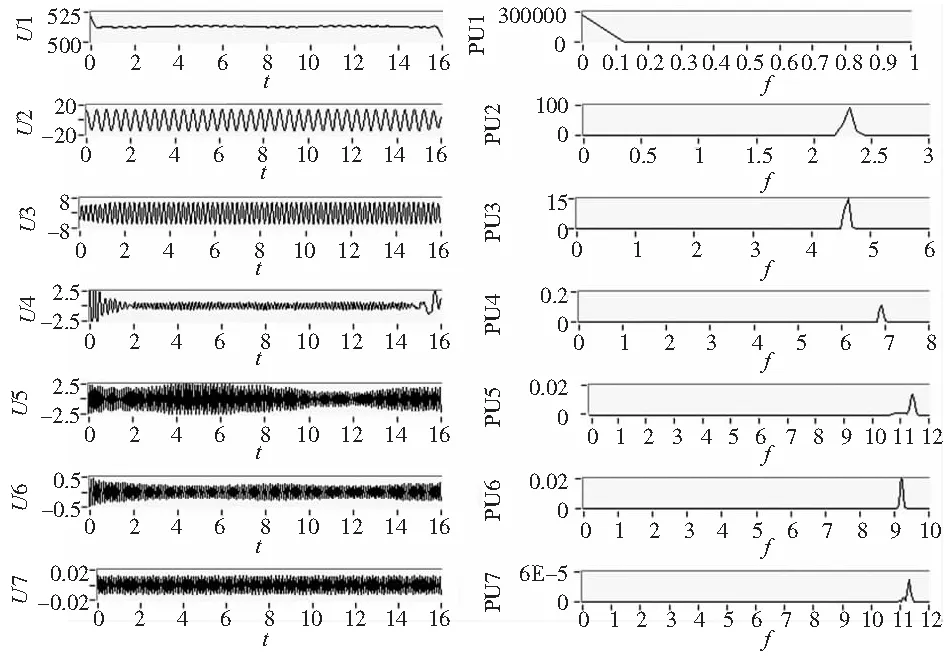
图4 信号S1的NSP分解及其功率谱

3.3.2 NSP分量能量分布

信号S1、S2、S3经NSP分解后均获得7阶分量，分量按式(8)、(9)计算能量分布，结果如下表。

表1 铣削功率信号的能量分布

从表1可以看出，3段铣削功率信号经NSP分解的2-4阶分量的能量占去除第1阶分量后信号总能量的百分比依次为99.34%、99.21%、95.89%。这表明铣削功率信号的能量在频域上虽分布广泛，但绝大部分能量集中在前4阶分量中，且能量分布不均匀。

3.3.3 NSP的自适应性分析

NSP和EMD一样，是自适应的信号分解算法，两种算法在分解中均没有固定的基函数，每个分量的提取由信号本身的性质决定，且分解出的分量与原信号相似。在数字信号处理中常用相关系数来表示两个信号的相似程度[7]，NSP分解的分量与原始信号相关系数的数据见表2。

表2 NSP分量与原始信号的相关系数

为探究功率信号能量分布与分量相关系数的关系，以分量为横坐标，能量分布和相关系数为纵坐标作图，见图5。从图5知，经NSP分解的分量能量分布与相关系数的变化趋势基本相同，两者的相关性很大，相关系数依次为0.972、0.997、0.988，均大于0.95。信号分量的能量分布与相关系数的相关程度越高，表明分解算法根据信号本身的固有特性进行自适应分解的能力越强。因此，分解铣削功率信号时，NSP算法具有良好的自适应性。

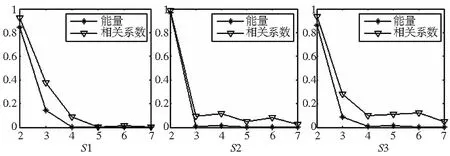
图5 NSP分量能量分布与相关系数

4 结论

(1)与EMD算法相反，NSP算法分解的第1阶分量是趋势项，随着分解的进行，分量的频率有逐步增大的趋势；

(2)铣削参数恒定时，功率信号经NSP分解的分量可分为两部分：静态分量和动态分量，静态分量是NSP分解的第1阶分量，动态分量呈周期性变化；

(3)铣削功率信号NSP分量的能量集中在前4阶，分量包含丰富的有关主轴状态和刀具状态等的信息；

(4)分解铣削功率信号时，NSP算法具有良好的自适应性。

[1] Hua Shao, Xinhua Shi, Lin Li. Power signal separation in milling process based on wavelet transform and independent component analysis[J]. International Journal of Machine Tools & Manufacture 2011,51: 701-710.

[2] Faleh A. Al-Sulaiman, M. Abdul Baseer, Anwar K. Sheikh. Use of electrical power for online monitoring of tool condition[J]. Journal of Materials Processing Technology 2005,166:364-371.

[3] 王海丽, 马春翔, 邵 华, 等. 车削过程中刀具磨损和破损状态的自动识别[J]. 上海交通大学学报, 2006, 40(12):2057-2062.

[4] Silong Peng, Wen-Liang Hwang. Null Space Pursuit: An Operator-based Approach to Adaptive Signal Separation[J]. IEEE Transactions on Signal Processing, 2010,58(5):.

[5] Silong Peng, Wen-Liang Hwang. Adaptive Signal Decomposition Based on Local Narrow Band Signals[J]. IEEE Transactions on Signal Processing, 2008 ,56( 7).

[6] 杨明伦, 邵 华. 基于EEMD和IMF能量分布的刀具破损识别[J]. 组合机床与自动化加工技术, 2013(4):54-58.

[7] 凌同华, 张胜, 易志强, 等. 岩石声发射信号能量分布征的EMD分析[J].振动与冲击, 2012,31(11):26-31.

[8] 石新华. 基于盲源分离技术的切削过程监控[D]. 上海：上海交通大学, 2010.

[9] 张贤达. 现代信号处理[M]. 北京: 清华大学出版社, 2002.

(编辑 李秀敏)

An Analysis of Power Signal in Milling Based on Null Space Pursuit

LI Yan-jia, SHI Xin-hua, SHAO Hua

(School of Mechanical Engineering，Shanghai Jiao Tong University，Shanghai 200240，China)

Power signal has been widely used in cutting condition monitoring because of its easy access and low costs. Therefore, it is essential to perform a deep analysis on the features of power signals. Decomposition of power signals was implemented by using null space pursuit (NSP) method, further more, characteristics of subcomponents obtained from the decomposition and its energy distribution were analyzed in the paper. The adaptability of NSP was also explored. Analysis results showed that the NSP subcomponents of power signals in milling were rich in cutting process related information, and the energy of the original signals concentrated on the first four subcomponents. It was also found that when milling parameters kept constant, a power signal could be divided into two parts: static component and dynamic component. Experiments demonstrated that NSP had an excellent adaptability when being applied in decomposing power signals in milling.

milling;power signal;null space pursuit;NSP

1001-2265(2014)05-0001-04

10.13462/j.cnki.mmtamt.2014.05.001

2013-09-05

国家自然科学基金项目(51075276)

李衍佳(1989—)男，湖南浏阳人，上海交通大学硕士研究生，主要从事切削过程监控及切削机理的研究，(E-mail)lyj_zp2011@163.com。

TH166;TG65

A