基于反馈控制的插电式混合动力汽车电池模块控制系统部件互换模块化的研究*

林 程，周逢军，曹万科，王 刚，2，南金瑞

(1.北京理工大学，电动车辆国家工程实验室，北京 100081; 2.山东交通学院，济南 250023)

前言

随着汽车控制系统中电控单元组件的增多，控制系统的设计、制造、维护过程的标准化要求也随之提高。汽车控制系统中的组件发生改变时，系统控制器和组件控制器均须重新设计，包括标定的更新。控制系统中采用组件互换模块化(component swapping modularity，CSM)进行设计时，当控制系统组件发生改变时，系统控制器无须重新设计，控制器的再标定工作只需在组件控制器中进行［1－2］，因此对汽车控制系统进行CSM设计可以增加组件之间的互换性，缩短开发时间和降低开发成本［3］。

目前用来处理控制系统组件发生改变的方法主要有鲁棒控制、自适应控制和增益系数调度控制，但这些方法在一定程度上不大适用于大组件的变动［3］。传统方法中的鲁棒控制器能适应由制造公差、工况变化和组件自身老化所带来的参数变化，但不适用于交换组件时所造成的参数变化［4］。自适应控制器需要在线调整和复杂的实施步骤来保证对噪声抑制的稳定性、鲁棒性和激励的持续性，并且在工业应用中不允许出现自适应阶段递降的暂态特性［5］。增益系数调度控制要求微控制器有较大的内存空间和较强的计算能力，这将大大增加开发成本。因此本文中提出采用极点配置法对PHEV电池模块控制系统进行设计研究。

1 预备知识

1.1 状态反馈控制与极点配置

把系统状态变量按一定的比例关系，反馈到系统输入端的形式称为状态反馈，设线性系统［6］为

而反馈规律为

式中:A、B、C、D、K 分别为 n×n、n×m、p×n和 m ×n矩阵，v为参考输入。令v=0，则状态反馈的闭环系统的状态空间表达式为

状态反馈系统框图如图1所示。闭环系统极点的分布情况决定了系统的稳定性和动态品质，比较式(1)和式(3)可知，状态反馈前后的系统矩阵分别为A和(A+BK)，特征方程分别为det(λI－A)=0和det［λI－(A+BK)］=0，因此状态反馈系统的极点不仅与系统本身的结构参数有关，而且与状态反馈K有关，据此可对控制系统极点进行配置，并使系统的极点保持在左半平面，以保证系统的稳定性。

1.2 PHEV控制系统简介

PHEV储能电池主要在两种模式下工作［7］:耗电模式(charge deleting，CD)和电量保持模式(charge sustaining，CS)。PHEV在电池充满电时，工作在CD模式，即纯电动模式，储能电池向驱动电机提供电能，电机作为唯一的动力源驱动车辆。储能电池SOC整体上趋于下降的趋势，在制动能量回收时，会有波动出现。当电池SOC降到参考值时，控制系统进入CS模式工作，类似于传统混合动力电动汽车的工作模式，储能电池SOC会波动，但整体平均值维持在同一水平。因此文中在PHEV电池控制系统设计中，将SOC作为电池唯一的状态变量。

2 PHEV电池控制系统建模

如前所述，由于电池工作在CD模式时，PHEV处在纯电动模式，发动机不参与工作，因此本文中主要对CS模式下的电池控制系统建模，PHEV电池模块CS模式控制系统示意图如图2所示。整车控制器根据工况计算得到实际功率需求Prw，控制系统根据电池状态反馈信息x，在发动机和电池模块之间进行功率分配，并分别向发动机和电动机发送功率需求命令Pre和Prb。电动机和发动机根据分配的功率需求命令驱动车辆前进。

根据上述控制系统的逻辑分析，建立数学模型:

式中:K1、K2为状态反馈增益向量，K1=［k1，k2，k3］T，K2= ［k4，k5，k6］T;q1、q2为前馈增益;ce、cb为组件控制器增益，表示控制器之间信息的相互传递。状态空间变量 x= ［x1，x2，x3］T，具体表达式为

电池SOC变化率与电池放电功率的关系［8］为

式中:bh是和电池硬件系统相关的参数。根据式(5)和式(6)可知 x3和 x1、x2线性相关，可用 x1、x2线性表达。

设式(4)闭环控制系统极点为 p1、p2、p3，系统中电池的效率为ηb，电机的效率为ηm，发电机的效率为ηg，则由反馈控制系统极点配置可得控制器反馈增益［9］为

从以上公式可知，k4可用k1表示，k5可用k2表示，而k6=0。因此需要优化的参数为k1、k2和k3。以功率跟随累计误差、发动机燃油消耗和电池等效燃油消耗建立目标函数如下:

其中:

3 仿真分析

以BFC6110HEV旅游客车为设计参考对象，根据式(4)～式(7)，基于BUSRTE工况(图3)进行仿真，分别对4种不同容量的电池组件控制器参数进行优化。表1和表2分别列出了整车和电池基本参数。SOC参考值选取时，须考虑［9］:(1)为了尽可能使用CD模式，SOCk的取值应尽可能小;(2)为了满足CS模式下电池能量的使用需求，SOCk应足够大。因此，SOCk可根据CS模式下的能量需求进行选取，较小容量的电池模块，要取较大值，较大容量的电池模块SOCk可取较小值。4种电池模块的设计参数取值见表3。整个工况循环中，4种电池SOC变化曲线如图4所示。

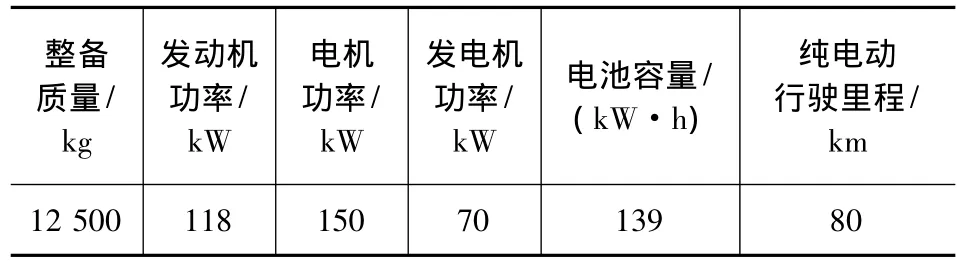
表1 整车基本参数

表2 电池基本参数

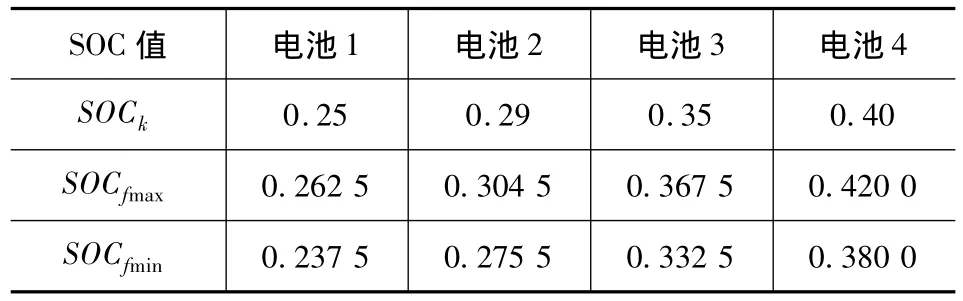
表3 电池设计参数

以设计参考车型电池2模块参数为基准参数，根据式(7)和式(8)，应用Matlab中fmincon函数，进行非线性约束优化求解，得到电池2的控制器增益参数k1=305.868，k2=0.458 575，k3=6.881 817。电池2 的工况循环功率曲线见图5(a)，功率跟随误差曲线见图5(b)。将电池2的控制器增益参数分别用于电池1、电池3、电池4控制系统，得到发动机功率变化曲线和功率跟随误差曲线分别如图6～图8所示。

从图5～图8可以看出，电池模块提供的功率变化幅度大，在尽可能提高电池模块功率的同时，SOC变化偏移量能始终保持在容许范围内，发动机功率变化较为平缓，可满足循环工况使用需求。虽然高能量的电池模块能够提高大的需求功率，但是其质量大造成其需求功率也大，等效燃油消耗也相对较高，但整体上表现出良好的燃油经济性，如表4所示。电池2的控制系统增益值用于电池1、电池3、电池4系统仍能表现出良好的特性，证明各电池模块之间具有互换性，对电池2的控制系统具有兼容性，能满足CSM的要求。

表4 车辆性能优化结果

4 结论

本文中采用反馈控制法进行极点配置的PHEV电池模块控制系统，通过多约束非线性优化得到的控制器反馈增益，并用于不同容量的电池模块控制系统设计中，提高了不同电池模块之间的互换性和兼容性。通过工况循环仿真的结果表明，整车具有良好的经济性和电量保持性，因此采用反馈控制极点配置法设计的控制器能够满足电池模块CSM需求，这对电动汽车整车控制系统模块的开发设计具有指导意义。

［1］Ulrich K，Tung K.Fundamentals of Product Modularity［J］.Harvard Business Review，1997，75:84 －85.

［2］Zhang Y，Gershenson J K，Prasad G J.Product Modularity:Measures and Design Methods［J］.Journal of Engineering Design，2004，15:33－51.

［3］Li S，Kolmanovsky I V，Ulsoy A G.Direct Optimal Distributed Controller Design for Component Swapping Modularity with Application to ISC［C］.Proceedings of American Control Conference，Marriott Waterfront，Baltimore，MD，USA，June 30－July 02，2010.

［4］周克敏，毛剑琴.鲁棒与最优控制［M］.北京:国防工业出版社，2006.

［5］韩正之，陈彭年，陈树中.自适应控制［M］.北京:清华大学出版社，2011.

［6］刘豹，唐万生.现代控制理论［M］.北京:机械工业出版社，2011:14－15.

［7］丁云波.Plug－in混合动力轿车动力管理策略的仿真研究［EB/OL］.［2012－02－04］.http://www.doc88.com/p－057205562469.html.

［8］Di Cairano S，Liang W，Kolmanovsky I，et al.Engine Power Smoothing Energy Management Strategy for a Series Hybrid Electric Vehicle［C］.2011 American Control Conference，San Francisco，CA，USA，June 29 －July 01，2011.

［9］Lester Faleiro，Jean－François Magni，Jesús M.de la Cruz ，et al.Eigenstructure Assignment［J］.Robust Flight Control，1997，224:22－32.