基于行驶工况特征的汽车燃油消耗的预测*

姜 平，石 琴

(1.合肥工业大学机械与汽车工程学院，合肥 230009; 2.合肥工业大学交通运输工程学院，合肥 230009)

前言

汽车燃油消耗与其自身特性、道路交通状况、自然环境和驾驶水平与习惯有关［1］。到目前为止，国内外针对汽车自身特性的燃油消耗研究较多，并且相应的节油技术在汽车设计、制造和使用方面已得到了广泛的应用，相比之下，针对其它因素的研究较少，因此研究道路交通状况下汽车行驶特征对燃油消耗规律具有现实意义。文献［2］～文献［4］中考虑了速度和加速度等较少的参数，直接采用线性回归对燃油消耗进行预测。文献［5］～文献［8］中对城市道路燃油消耗多局限于城市道路瞬态消耗的研究，预测模型只是单纯考虑速度或加速度等特征参数与燃油消耗的关系。回归分析方法属于传统的预测方法，对变量之间的因果关系进行分析时，存在多重共线性和序列相关等问题，模拟效果不佳。人工神经网络具有很强的自适应、自学习和纠错能力。本文中针对汽车在城市典型道路行驶工况中的特征参数与燃油消耗之间的关系进行实际燃油消耗预测。通过主成分分析方法(principal component analysis，PCA)提取影响燃油消耗的主成分，克服了影响因素间相关性的问题，简化BP神经网络的输入单元数，提出典型道路行驶工况燃油消耗的预测模型，为目前国内构建城市典型道路行驶工况的燃油消耗预测模型提供了新的方法。

1 实际燃油消耗的影响因素

汽车在实际行驶过程中影响其燃油消耗的因素很多，除汽车自身性能(如发动机功率、燃油消耗率、转速、传动系传动效率、传动比等)，还取决于道路状况、交通环境和汽车的行驶工况等因素。车辆运行过程中的一些影响因素(行驶速度、加减速度、怠速时间等)对燃油消耗有重要影响。本文中从汽车在典型道路上的行驶工况方面来分析汽车实际燃油消耗。

行驶工况又称汽车运转循环［9］，是指在特定行驶环境下，汽车在一定的道路路网中行驶的速度-时间变化规律。汽车行驶工况可由不同的行驶特征参数来区分。文献［10］中经过多次选用不同的特征参数做主成分分析后，最终选出13个特征参数来描述和评价行驶工况的特征并进行了计算，它们是最大速度vmax(km/h)、平均速度vm(km/h)、行驶速度vmr(km/h)、速度标准偏差vsd(km/h)、最大加速度amax(m/s2)、平均加速度aa(m/s2)、最小减速度amin(m/s2)、平均减速度ad(m/s2)、加速度标准偏差asd(m/s2)、加速比例 pa(%)、减速比例 pd(%)、匀速比例pc(%)和怠速比例pi(%)。百公里油耗是评价汽车燃油经济性的一项重要评价指标，本文中以实际百公里燃油消耗作为燃油消耗的评价指标，计算式为

式中:q为汽车实际的燃油消耗量，L;S为汽车的行驶路程，km。

2 基础理论

2.1 主成分分析［11］

由于影响燃油消耗的变量因素很多，完全用特征参数来对大量行驶片段进行预测，计算将很复杂。特别在神经网络预测方法中，由于输入节点过多而经常导致网络收敛慢、预测精度低。虽然每个影响因素变量都提供了一定的信息，但变量之间有一定的相关性，并不完全独立，从而使这些变量所提供的信息在一定程度上有所重叠［12］。

主成分分析是一种处理高维数据的方法，其思想就是降维，减少变量的个数。设有p个有一定相关关系的变量表示原始指标，记为 X1，X2，…，Xp，样本数为n，则观测样本数矩阵为

主成分分析的计算过程如下。

(1)将原始数据进行标准化变换

(2)计算相关系数矩阵

(3)利用雅克比法求矩阵R的非负特征值和对应于特征值的特征向量

(4)选取主分量

假设有p个变量则最多有p个主成分，保留多少个主成分取决于累积贡献率的大小。选取前m个(m＜p)主成分，使其累积贡献率达到一定要求(如大于80%)，以前m个主成分代替原始数据进行分析，这样便可达到降低原始数据维数的目的。

2.2 BP 神经网络［13］

BP网络是利用非线性可微分函数进行权值训练的多层网络。BP网络能学习和存贮大量的输入-输出模式映射关系，无须事前揭示描述这种映射关系的数学方程。

一般BP神经网络模型的拓扑结构包括输入层、中间层(隐层)和输出层。隐层的神经元个数很难确定，而且在很大程度上影响网络的预测性能。隐层神经元个数n2和输入层神经元个数n1之间有如下近似关系:

根据式(6)初选隐层神经元的个数，再经过实际的检验训练。对初选的隐层神经元数进行调整，当网络误差最小时，就找到了一个最佳的隐层神经元。

3 实际燃油消耗的预测

3.1 实验数据采集

试验车为某款微型轿车。测试系统由综合性能检测平台﹑油耗测试系统和速度测试系统组成。实验方法为道路循环试验法，按照规定的路段和规定的时间进行单车试验，速度信号采样频率为1Hz。在城市交通流量调查中发现，城市内不同区域、不同等级道路对应着不同的交通流量和不同的车辆行驶工况。本文中选取了合肥市屯溪路、明光路等5条典型路段进行实验，每条路线作为一个行驶片段，采集的数据包括:步长为1s的瞬时速度、行驶时间、行驶距离和油耗值。研究表明，一天内的交通流早晚呈对称趋势，因此试验时间选取为每天下午高峰期和平常期，即下午3:00～6:00。为使采集的数据能反映合肥市整体道路的交通情况，统计数据具有代表性，进行了多次试验，收集了大量实验数据，选取较优的数据进行分析。行驶工况的部分速度和加速度与时间的曲线如图1所示。

3.2 主成分分析法的主要参数分析

对合肥市典型道路行驶片段特征参数和燃油消耗进行分析，得到了包含13个特征参数的96个行驶片段样本。行驶片段样本的特征参数值如表1所示。

利用SPSS统计软件对得到的行驶片段样本的13个特征参数值进行主成分分析，得到13个主成分。主成分得分可以代替特征参数来描述原行驶片段的行驶特性，只需少量主成分即可反映原来较多特征参数才能反映的行驶特性。

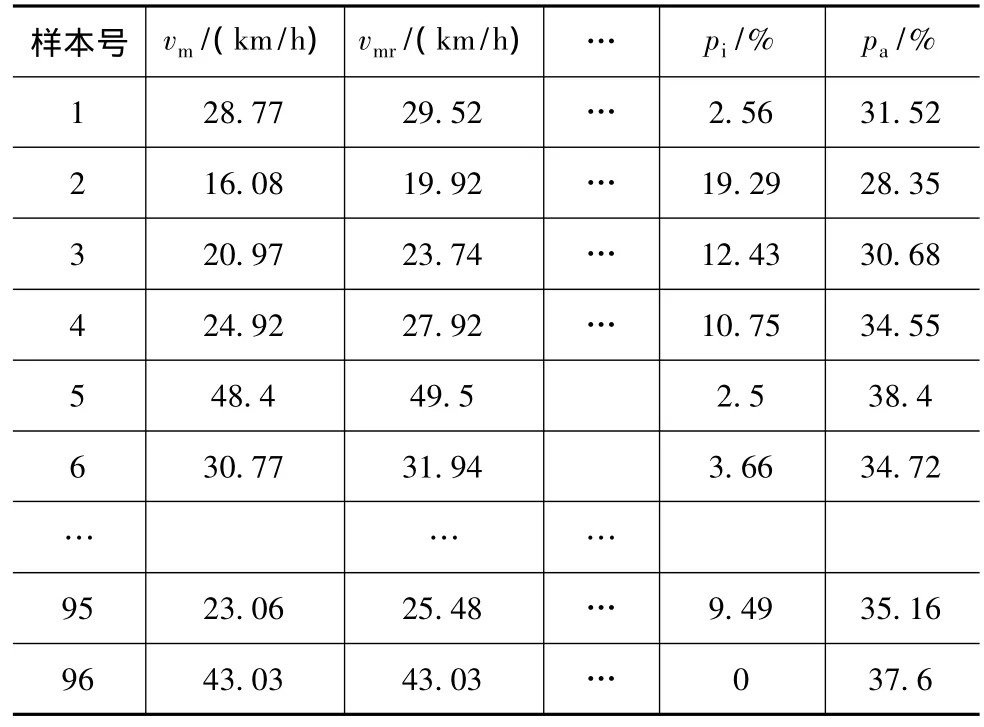
表1 所有行驶片段及其特征参数值

(1)主成分累积贡献率

表2给出了13个变量的主成分特征值和累积贡献率。前3个主成分的累积贡献率为84.776%，所以选取这3个主成分进行分析。

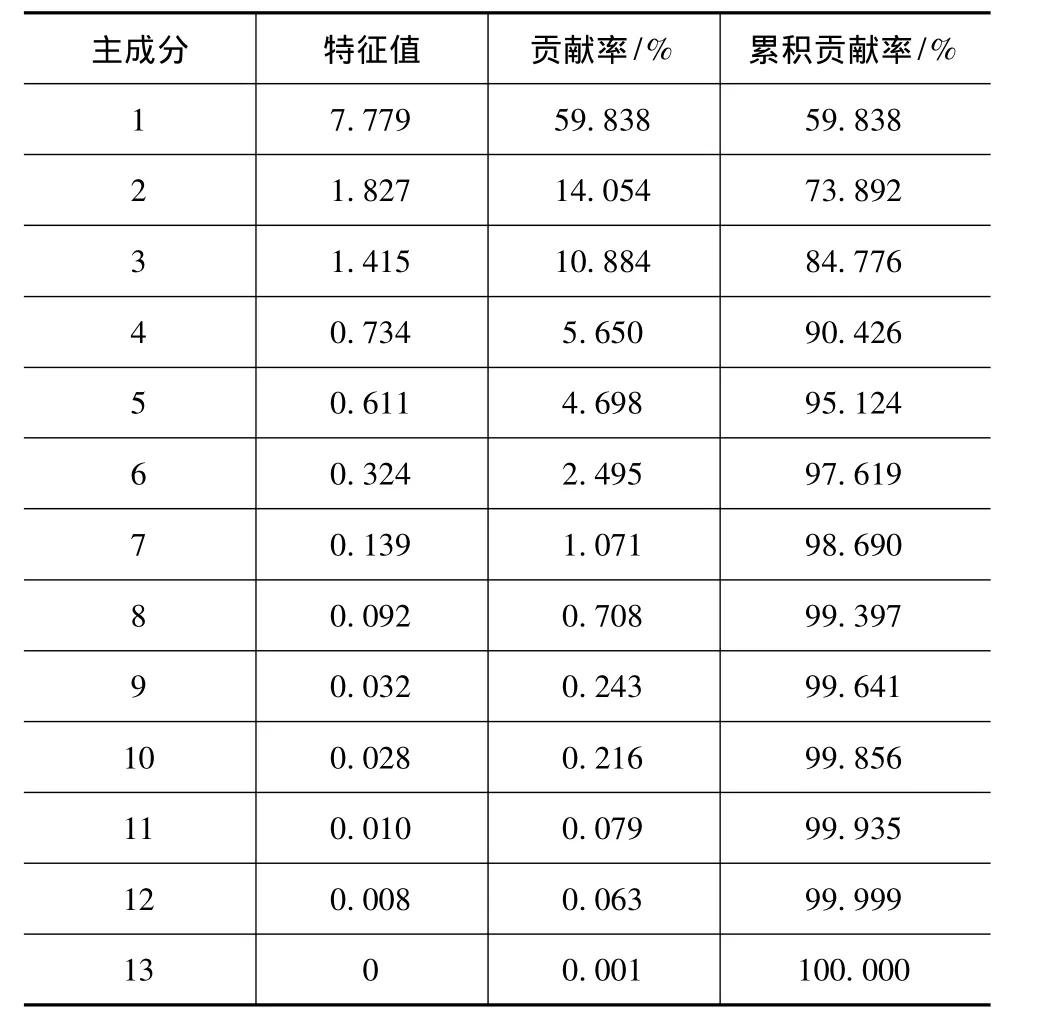
表2 各主成分的特征值和累积贡献率

(2)主成分载荷矩阵和得分矩阵

表3为主成分载荷矩阵。主成分载荷矩阵为参数在某个主成分上的载荷系数。一般如果载荷系数大于0.5，就表明该参数与这个主成分相关。根据这个原则，则这3个主成分所反映的主要特征参数如下:

①第1主成分主要反映最大速度、平均速度﹑行驶速度﹑最大加速度、最小加速度﹑加速比例、减速比例和怠速比例;

②第2主成分主要反映平均速度﹑行驶速度、最大加速度、平均加速度、最小减速度、平均减速度和加速度标准偏差;

③第3主成分主要反映最大速度、速度标准偏差和匀速比例。

从3个主成分与特征参数的关系也可以看出，3个主成分在很大程度上能反映13个特征参数的性质。所以3个主成分得分能代替13个特征参数来描述原行驶片段的行驶特性。因此下文的神经网络分析的样本输入(方法1)时取所有行驶片段的前3个主成分得分进行分析，如表4所示。

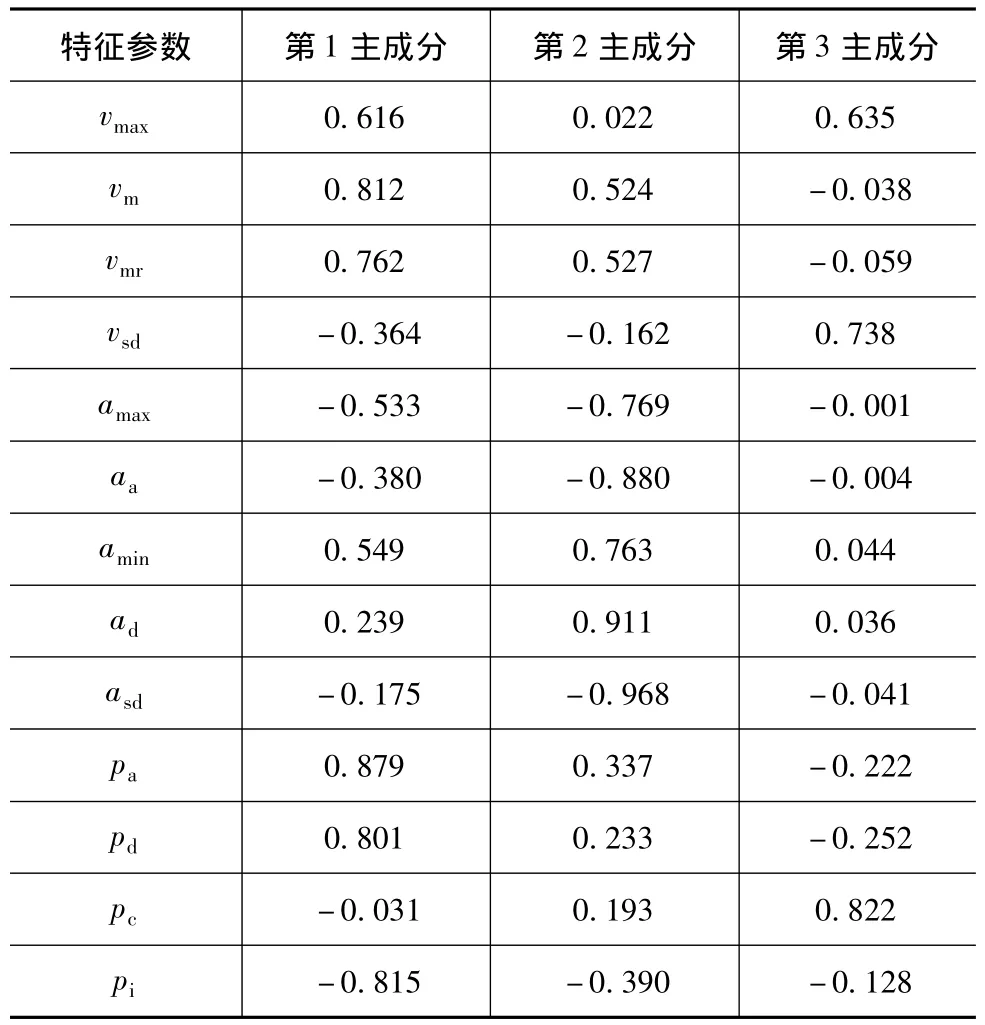
表3 主成分载荷矩阵

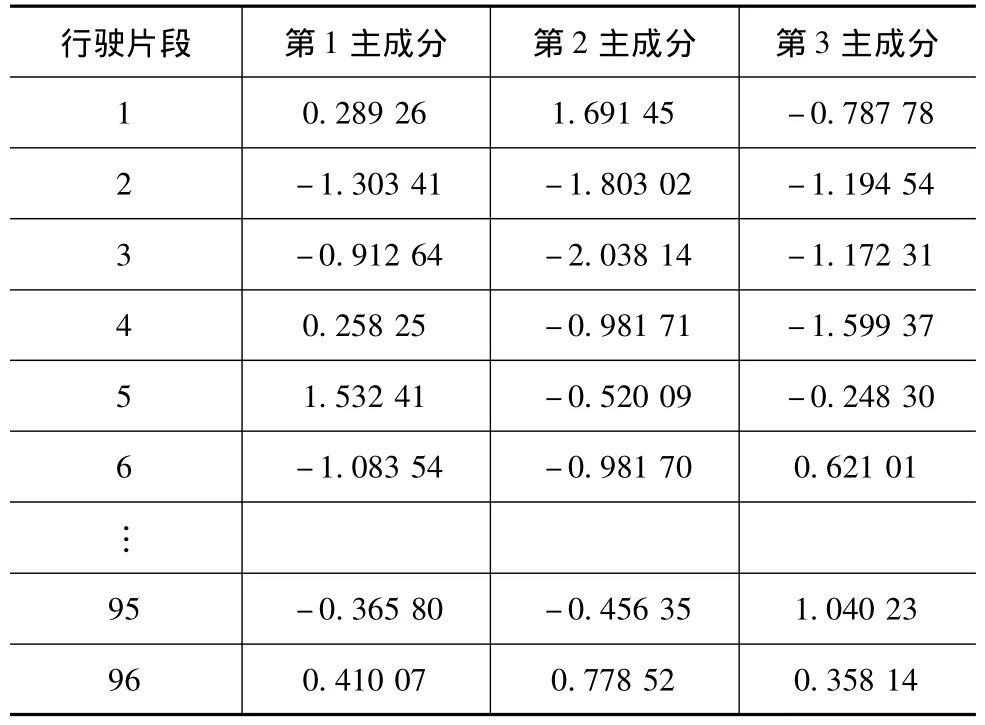
表4 主成分得分矩阵

3.3 BP神经网络设计

为了进一步说明本文所用方法的预测效果，在相同训练参数条件下，即网络最大训练次数为1 000、网络训练目标为0.000 1时，分别采用传统BP神经网络模型与主成分和神经网络结合的模型进行燃油消耗预测和比较。在预测分析之前，对样本的输入和输出数据进行归一化处理，将样本数据统一归化到区间［0，1］之间。两种方法如下。

方法1:选取表4样本数据中的前86个行驶片段的前3个主成分得分作为训练样本的输入，后10个行驶片段的前3个主成分得分为测试样本的输入。网络输出为汽车实际的百公里油耗。网络输入层为3个神经元，即3个主成分，中间层为6个神经元，输出层为1个神经元。中间层神经元传递函数为S型正切函数。输出层神经元的传递函数为S型对数函数，学习速率是自适应的。

方法2:先不提取主成分，而是直接使用原始数据作为网络输入。与方法1对应的表1中的前86个原始样本特征参数值为训练样本的输入，后10个行驶片段特征参数值为测试样本的输入。网络输出为汽车实际百公里油耗。输入层为13个神经元，中间层为27个神经元，输出层为1个神经元。中间层神经元的传递函数为S型正切函数。输出层神经元的传递函数为S型对数函数，学习速率是自适应的。

4 结果分析

经过训练，主成分和BP网络结合的方法的网络经过78次迭代就达到了训练目标。而直接采用BP网络方法经过145次迭代才达到训练目标，收敛速度慢。方法1与方法2预测的实际百公里油耗与原始数据的比较如图2所示。从图中可以看出，3条折线形状接近，趋势一致。

方法1所有样本预测值与实际值之间的平均相对误差为1.72%，均方根误差为2.55%。方法2所有样本预测值与实际值之间的平均相对误差为2.55%，均方根误差为3.25%。结果表明，经过主成分和神经网络结合的预测方法预测精度高，更能反映城市道路汽车实际的百公里燃油消耗。

5 结论

(1)从行驶工况特征参数方面分析了影响实际燃油消耗的因素，以实际百公里燃油消耗为评价指标，建立了实际百公里燃油消耗预测模型，为预测城市典型道路行驶工况的实际百公里油耗提供了新的思路。

(2)通过主成分分析引入了13个行驶工况特征参数，提取前3个主成分。未经主成分分析的BP神经网络输入神经元数为13。基于主成分分析的BP神经网络输入神经元数为3，从而降低神经网络的输入维数，简化网络结构，收敛速度快。

(3)利用组合方法预测城市道路实际百公里燃油消耗与单纯采用神经网络方法相比，试验数据的误差小，构建的预测模型能较准确地反映城市道路上汽车的实际燃油消耗与行驶工况的关系。

［1］高磊.基于城市道路工况的汽车燃油消耗模型研究［D］.长春:吉林大学，2007.

［2］Ergeneman M，Sorusbay C，Goktan A.Development of a Driving Cycle for the Prediction of Pollutant Emissions and Fuel Consumption［J］.International Journal of Vehicle Design，1997，18(3/4):391－399.

［3］Tzeng G H，Chen J J.Developing a Taipei Motorcycle Driving Cycle for Emissions and Fuel Economy［J］.Transportation Research Part D，1998，3(1):19 －27.

［4］Ericsson E.Independent Driving Pattern Factors and Their Influence on Fuel-use and Exhaust Emission Factors［J］.Transportation Research Part D，2001(6):325 －345.

［5］姚志良，马永亮，贺克兵，等.宁波市实际道路下汽车排放特征的研究［J］.环境科学学报，2006，26(8):1229 －1234.

［6］隗海林，王劲松，王云鹏，等.基于城市道路工况的汽车燃油消耗模型［J］.吉林大学学报(工学版)，2009，39(5):1146－1150.

［7］马冬，丁焰，刘志华，等.轻型汽车实际行驶工况的排放研究［J］.安全与环境学，2008，8(5):66 －68.

［8］张金武，石琴，朱俊虎.基于车辆行驶特征的燃油消耗分析［J］.科技传播，2011(6):194 －195.

［9］余志生.汽车理论(第3版)［M］.北京:机械工业出版社，2010.

［10］马志雄.典型城市公交车实际行驶工况的开发及研究［D］.武汉:武汉理工大学，2003.

［11］李友文.混合交通环境下行驶工况构建方法的研究［D］.合肥:合肥工业大学，2010.

［12］范金城，梅长林.数据分析［M］.北京:科学出版社，2002.

［13］飞思科技产品研发中心.神经网络理论与MATLAB 7实现［M］.北京:电子工业出版社，2006.