五轴加工中非线性误差的分析与研究
代子阳,谢明红
(华侨大学机电及自动化学院,福建厦门361021)
在对大型复杂的零件 (如发动机叶轮和叶片,大型箱体及高精度的复杂模具等)进行加工时,三轴数控机床越来越不能满足要求,取而代之是五轴数控机床。在加工复杂曲面时,有很多方面的因素(如机床精度、刀具与工件的弹性变形和热变形等)都会对五轴机床的加工精度产生影响,从而造成与实际曲面的不一致性,以至于产生很大的误差。文中所述的非线性误差是由于实际走刀轨迹与理论走刀轨迹的不一致性造成的。理论走刀轨迹要求刀具与工件表面相对运动是非线性的;然而由于目前的数控插补系统一般只能进行线性插补,由于旋转轴的加入使得刀具与工件表面的实际相对运动为非线性;造成实际走刀轨迹与理论走刀轨迹之间发生了偏差,称为非线性误差[1]。它是五轴加工所特有的。所以,在进行五轴加工时如何控制非线性运动误差是目前研究的一个热点问题。
1 五轴加工非线性误差理论分析
在前置处理中,由CAD/CAM生成的刀位轨迹时,是通过微小直线段来逼近工件模型的轮廓来实现。因此在加工过程中,只有实际运动为直线运动的刀位点才能符合实际编程精度。在五轴数控加工中,由于两个旋转轴的加入,造成了数控加工的非线性,导致了机床各轴的合成运动不再是直线而是一条条空间曲线。使得实际刀位运动严重偏离理论轨迹,造成误差严重影响加工精度和效率。所以,要进行误差计算,对超差部分作必要的修改,使误差控制在允许的范围内。
1.1 非线性误差产生的原因
在生成刀位文件时,把自由曲面按一定的精度来划分成微小的直线段,并假设只有刀具运动而工件不动原则来生成刀位轨迹。由于曲面曲率不断变化,必然引起刀轴矢量的不断变化。因此,只有在三轴加工时,才能获得理想的直线段。五轴联动时,由于旋转轴的加入,同时加上五轴数控系统是一个非连续轨迹控制系统,相邻两个刀位点之间轨迹不再是直线而是空间曲线[2]。由于非线性误差是在相邻的刀位点之间产生的,所以研究非线性误差不应该在整个刀位轨迹上,而应该分段进行。图1为相邻两个刀位点间,理想轨迹与实际插补轨迹的仿真图。

图1 为相邻刀位点间,理想轨迹与实际插补轨迹的仿真图
1.2 非线性误差的模型建立
图2显示了非线性误差产生的原因。由于在进行五轴双转台加工时,3个平动轴的运动过程容易想象,两个旋转轴的运动不易想象,也不易用视图显示。按照工件不动刀具运动的原则,可把它想象成刀具相对于工作台的摆动。图2中显示了两个刀位点C1、C2之间实际轨迹曲线与理论曲线形成的过程。在理想的情况下,要求刀具的旋转中心轨迹应按经过OiO'mOj的曲线运动。但是,由于目前的数控系统一般只能按照图中经过OiOmOj的直线轨迹进行插补运动,从而造成了实际轨迹曲线rs(图中虚线轨迹)与理论轨迹rl(图中实线轨迹)之间的偏差。根据微分几何,严格的非线性误差的计算可由公式 (1)精确地描述:

在实际中为了准确计算非线性误差,需要对rl和rs进行离散。经过离散化之后的非线性误差的计算为:
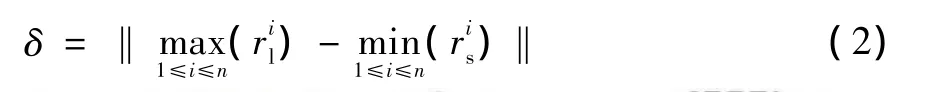
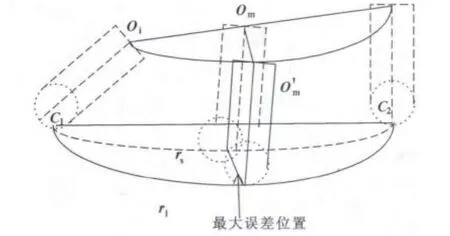
图2 非线性误差模型
严格非线性误差的计算不仅要知道待加工工件表面的几何信息和刀具信息,而且对曲面包络面的求解也很困难。然而对五轴后置处理时的刀位文件中上述信息并不存在,因此只能根据非线性的理论进行分析,并简化模型[3]。
1.3 最大非线性误差位置预测
下面以A-C双转台五轴数控机床为例,来预测最大非线性误差的位置。假设两个刀位点数据 (p1,r1)和 (p2,r2),以及刀触点分别为T1、T2投影到xOy平面如图3所示。由于数控插补系统是按线性进行插补的,所以过刀位点 (p1,r1)和 (p2,r2)的直线方程为:
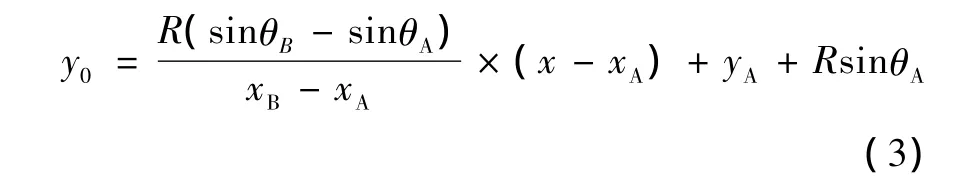
同样的角度变化如公式 (4)所示:
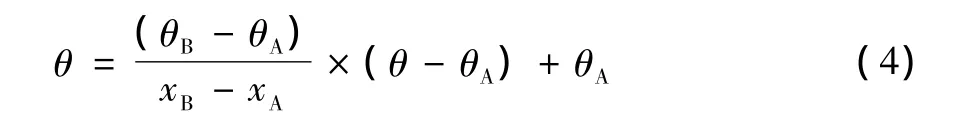
由公式 (3)、(4)可得刀触点的轨迹方程,如公式 (5)所示:

将y分别对x求一次导数和二次导数可得:
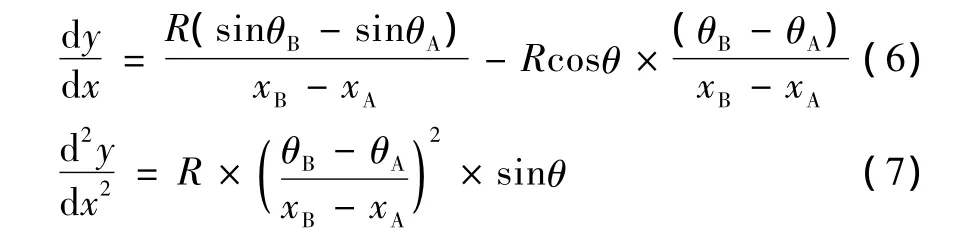
令其一次导数为零,可以预测出最大非线性误差的位置。

由公式 (8)得,最大非线性误差产生的位置为两个刀位点的中点附近。其中公式中的R为刀具半径。

图3 xOy平面上刀位点和刀触点的投影
1.4 求解非线性误差的方法
前几节已经预测出两个刀位点插补轨迹间非线性误差产生的最大位置。但是如果采用图2的模型来求解非线性误差,就需要知道模型轮廓的表面信息以及刀具的信息等。但是由于CAD/CAM软件生成的刀位文件中已经不包括这些信息,因此,文中采用机床运动学正反解的方法来求出非线性误差的大小。按照理想的情况,两个刀位点p1、p2的轨迹应该是一条直线pl,可是由于五轴数控插补系统只能进行线性插补,从而造成了两个刀位点p1、p2的插补轨迹为一条空间曲线ps如图4所示。
首先根据机床运动学的正解,求出在工件坐标系下的对应刀位数据点p1、p2转换到机床坐标系下,得到各个运动轴分量分别为 (x1,y1,z1,A1,C1)和 (x2,y2,z2,A2,C2)。然后根据数控系统的插补特性,获得任意时刻机床各运动轴的运动分量。最后,再利用机床运动学的反解法,把机床坐标系下任意时刻机床各轴的运动量转换成对应工件坐标系下各时刻刀具刀位点的坐标。最后求得各个刀位点与理想直线pl的距离h,如果距离h超过了允许误差,就要在这两个刀位点产生最大的误差位置插入新的刀位点,来达到减小误差的目的。
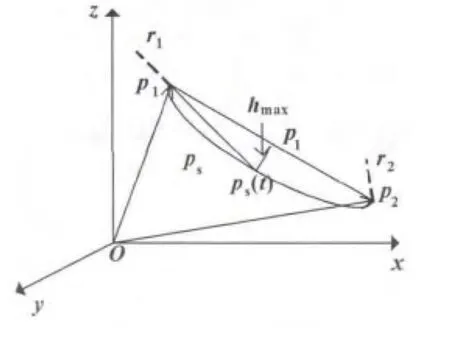
图4 两个刀位点p1、p2的插补轨迹
求非线性误差的步骤如下:
(1)首先求出在工件坐标系下的对应刀位数据点p1、p2对应机床坐标系下各个运动轴分量分别为(x1,y1,z1,A1,C1)和 (x2,y2,z2,A2,C2)。由于数控系统的线性插补功能,计算出任意时刻的各个运动轴坐标。插补轨迹方程为:
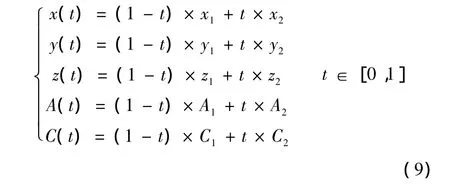
(2)利用机床运动学的反解法求出 (xt,yt,zt,At,Ct)对应的工件坐标系下刀位点的坐标ps(t)。
(3)在图5中,假设理想插补轨迹pl的单位方向矢量为n,则实际插补轨迹ps任意时刻的刀位点坐标ps(t)到单位方向矢量n的距离为h(t),则

对公式 (11)进行求导,得到当t=ts时,h(t)有最大值为hmax:

2 控制最大误差的策略及模拟仿真
目前对于非线性误差超差的情况,主要使用刀触点偏执法、线性化法和自适应线性化处理方法,来达到减小非线性化误差的目的,使其达到允许的误差范围的要求。
(1)刀触点偏执法。该方法是为了消除工件加工过程中的过切和欠切现象,将刀具沿着刀触点的法线方向偏执一定的距离,改变误差的分布,但是该方法无法偏执过后的误差在允许的范围内,无法达到精确控制的目的[4]。
(2)线性化法。是将所有插补段线性分割,加密走刀步数,减小因走刀步长过大引起的非线性运动误差,但是这种方法的缺点是,随着零件设计的曲面的复杂化,数控程序的数量会不断加大,因此在密化加工程序时,会加大加工程序的数量,影响数控加工的插补和译码能力,降低了数控加工的效率和加工能力[5]。
(3)自适应线性化法。该方法的思想是,首先计算出各个程序段的线性误差,只对超过许用误差的程序段进行线性分割再折半分割来减小刀位点位置和刀轴矢量的变化,该方法不仅可以减小非线性误差保证其不超过允许误差,并且消除了非必要的刀位密化,较线性化法可以提高机床的加工效率和插补译码的能力,最大限度地发挥了机床加工的能力[6]。
2.1 自适应非线性误差的控制方法
如前所述,在五轴加工时由于两个旋转轴的引入,使得在实际加工过程中刀具与工件的接触位置很难预测。再加上刀位数据中只有刀触点位置与刀轴矢量的描述,缺少刀具的实际形状和工件表面信息。因此,在五轴加工时很难预测出最大非线性误差出现在相邻刀位点的什么位置。但是,根据前面对最大非线性误差位置的预测和仿真验证,在实际中往往取两个刀位点中点位置作为新刀位点的插入位置。假设相邻两个刀位数据为 (pj,rj)、(pj+1,rj+1),首先计算出这两个相邻刀位点的误差,如果超差就插入新的刀位点 (pw,rw),然后再分别求出 (pj,rj)、 (pw,rw)和 (pw,rw)、(pj+1,rj+1)的误差,如果超差,就继续插入新刀位点,直到误差在允许范围内为止。

根据上述思想画出如图5所示的非线性误差控制程序流程图。
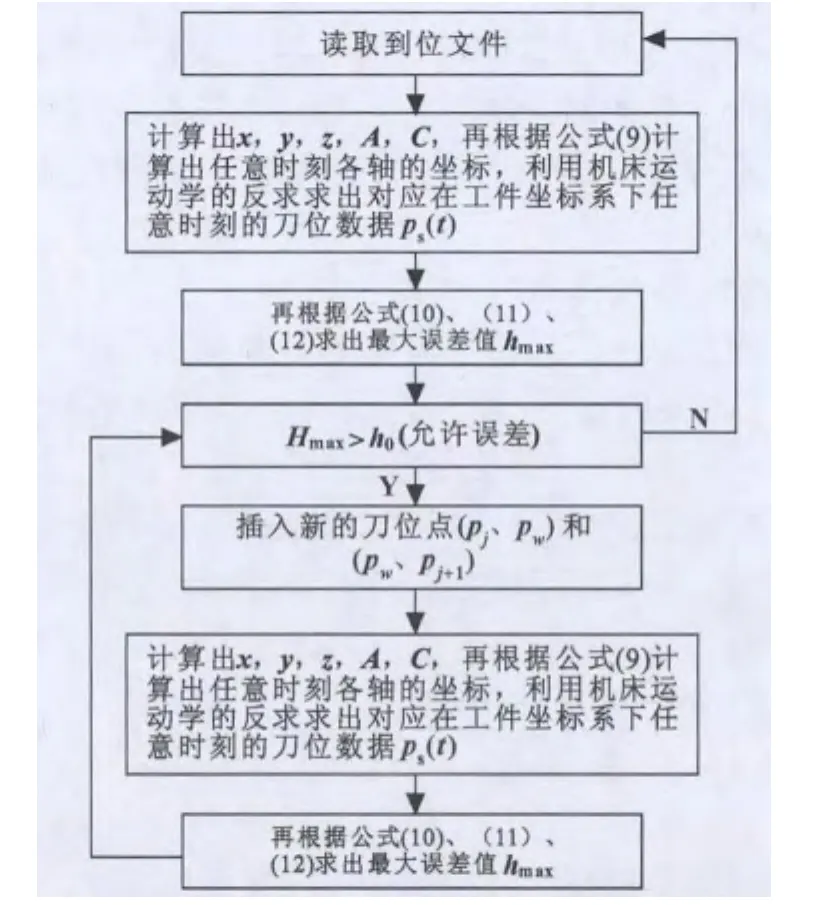
图5 非线性误差控制程序流程图
2.2 通过MATLAB软件对算法结果进行仿真验证
通过对橄榄球面的加工,验证上述减小非线性误差的正确与否。首先取出通过PRO/E生成的刀位文件中的10个采样点,对其进行误差计算。其误差分布图如图6所示。未经误差补偿的非线性误差结果偏大,其平均值大概在0.015 mm左右。
采取文中提出的减小非线性误差的算法,即在超差的相邻两个刀位点中间插入新的刀位点,来减小非线性误差。取最大非线性误差不超过0.9 μm。在对进行刀位数据补偿后,进行计算与仿真。其仿真结果如图8所示。从图中可以看到非线性误差有效的控制在0.9 μm之内。在没有进行非线性误差补偿前,只有10个刀位点;在非线性误差补偿后,刀位点个数增加到52个。从图7中可以看出,非线性误差补偿后明显达到了减小非线性误差的目的。
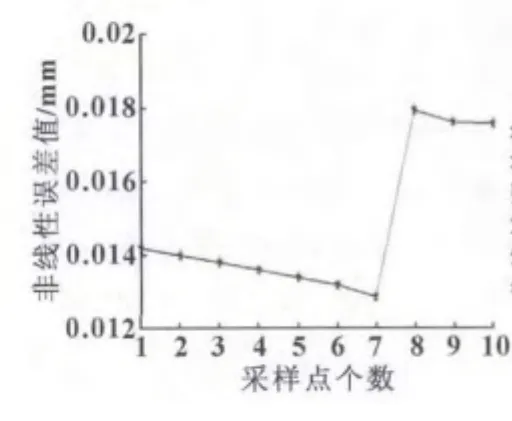
图6 非线性误差补偿前

图7 非线性误差补偿前后对比
通过上述仿真结果,说明了该方法的有效性,达到了减小非线性误差的目的。图8显示了对相邻两个刀位数据进行补偿前后的仿真图。补偿后的到位轨迹更加接近理想曲线。
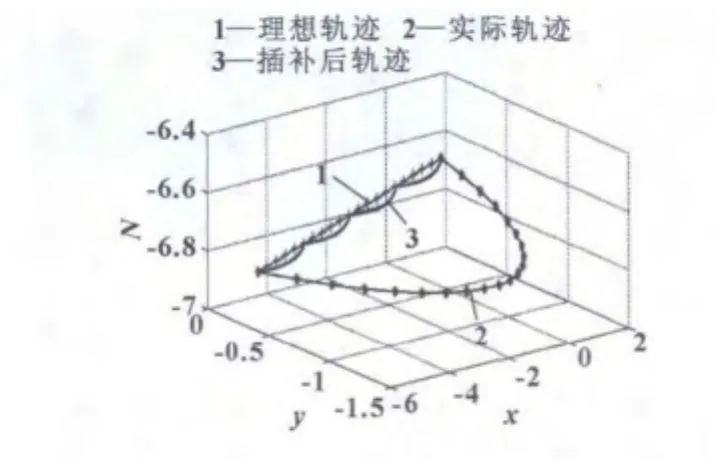
图8 非线性误差补偿前后的刀位轨迹
3 小结
非线性误差是五轴加工过程中不可避免的,也是其特有的。文中在基于双转台五轴数控加工的基础上,介绍了一种在两个相邻刀位点中间插入新的刀位点,并通过了MATLAB的仿真验证了该方法可以有效地减小非线性误差。弥补了CAM软件输出刀位文件对非线性误差没有考虑的缺陷[1]。
[1]吴大中.五轴联动数控加工非线性误差控制及后置处理[D].上海:上海交通大学,2007.
[2]范冬青,张洪.曲面数控加工中的非线性误差[J].机械设计与制造,2004,(4):35 -37.
[3]何永红,齐乐华.赵宝林双转台五轴数控机床后置处理算法研究[J].数控技术,2006(1):9-11.
[4]刘宏.复杂曲面多轴数控加工非线性误差理论分析及控制[J].组合机床与自动化加工技术,2003(12):66-68.
[5]TAKEUCHI Y,IDEMURA T.5-Axis Control Machining and Grinding Based on Solid Model[J].Annals of CIRP,1991,40(1):455-458.
[6]任秉银,唐余勇.数控加工中的几何建模理论及其应用[M].哈尔滨:哈尔滨工业大学出版社,2000:93.

