滚珠丝杠副载荷分布情况研究
张陈灵,范元勋
(南京理工大学 机械工程学院,江苏 南京 210094)
滚珠丝杠副载荷分布情况研究
张陈灵,范元勋
(南京理工大学 机械工程学院,江苏 南京 210094)
滚珠丝杠副受外载荷作用时滚珠的受力是比较复杂的,但目前在研究滚珠丝杠副滚珠受力时都是简单地按照均载来分析,这与实际的载荷分布情况有较大的偏差。建立一个变形协调条件下的滚珠丝杠副载荷分布的模型,并分析了几何误差对滚珠受载的影响。
滚珠丝杠副;载荷分布;几何误差
0 引言
滚珠丝杠副作为一种新型的螺旋传动元件,由于其高精度、高效率、优越的耐磨损性和高速特性以及运动可逆性等良好的机械性能,它在国内外工程技术界已经获得了广泛的应用,尤其是近年来其在航空工业的各个部门更是获得了高度的重视。而研究滚珠丝杠副的载荷分布情况是研究其一系列机械性能的基础。但是,目前在研究滚珠丝杠副载荷分布时都是简单地按照滚珠均匀受载来分析,这与实际的载荷分布情况有较大的偏差。因此,建立一个求解滚珠丝杠副载荷分布的模型显得十分必要。
1 数学模型的建立
1.1 滚珠丝杠副滚珠等效受力模型的研究
首先对单螺母滚珠丝杠副在丝杠受拉和螺母受压状态下(以下简称T-C状态)的受力进行分析,如图1所示。图中Fa0为滚珠丝杠副的轴向外载荷;Ds为丝杠的外径;Dn为螺母的外径;Fsi,Fni为丝杠和螺母对第i个球的轴向力。
为了有效地分析滚珠与滚道接触时的受力情况,将某个滚珠和滚道接触时的状态放大,如图2所示。图中βj为第j个滚珠和滚道间的接触角(j=1,2,3,…);Pj为第j个滚珠所受的法向载荷db为滚珠的直径;t为曲率比。

图2 滚珠在滚道中的接触状态图
为了方便分析,结合图1和图2建立一个如图3所示滚珠丝杠副滚珠等效受力的模型图,它清楚地显示了滚珠和滚道的接触状态。

图3 滚珠丝杠等效受力分析图
根据平衡受力情况和赫兹理论,丝杠和螺母对第i个球的轴向力,Fsi和Fni,可以由式(1)得来:
(1)
式中:Fa0——所受的轴向载荷;
Pj——第j个滚珠所受的接触力;
λ——滚珠丝杠的螺旋角。
由滚珠轴向外载荷和滚珠间的作用力关系可得:
(2)
式中:Z——滚珠的个数;
Pjsinβjcosλ——第j个球和滚道间接触力的轴向投影。
式(2)就是得到的轴向外载荷与每个滚珠法向载荷之间的关系。
1.2 考虑误差情况下变形协调关系的建立
在分析了滚珠丝杠副滚珠受力状态之后,来考虑滚珠受力时的变形情况。如图4所示,为了简化分析,把第i个滚珠,i-1个滚珠,螺母和丝杠轴的延螺旋角方向的接触状态放大出来。

图4 第i个滚珠和第i-1个滚珠在螺旋角方向的接触状态图
接下来研究滚珠受力时的变形协调关系。首先,给丝杠提供一个轴向力,这个轴向力使所有的滚珠都保持T-C状态。实际受载后,滚珠及滚道的几何误差(主要是滚珠的直径误差、丝杠副的导程误差)会导致的滚珠接触位置有所偏移。假设由于几何误差导致的所有接触位置误差不会改变初始的接触角。如图4所示,空间变形量在螺旋角的平面内。在接触点a和b,几何误差分别为σisinβi,σi-1sinβi-1。
图5显示的是丝杠单元的受力变形分析。ΔL表示第i个滚珠和i-1个滚珠间的距离。第i个球和滚道的接触点a和c的变形量εa和εc,它们会随着滚珠丝杠的轴向变形而改变。同样的,还有第i-1个球和滚道的接触点b和d的变形量εb和εd。
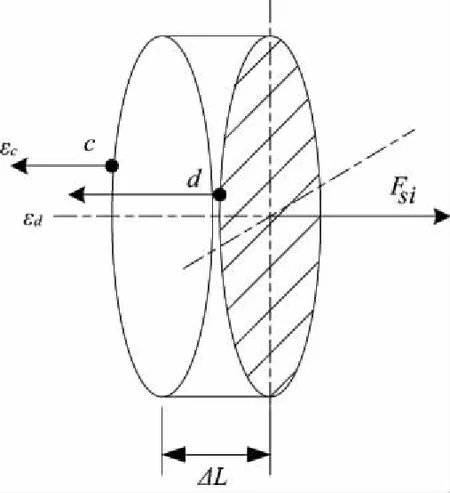
图5 丝杠单元变形受力分析图
在T-C状态下,丝杠c点和d点之间的轴向位移变化量是εsi,螺母a点和b点之间的轴向位移变化量是εni。他们可以由式(3)和式(4)得到:
εsi=εc-εd
(3)
εni=εb-εa
(4)
结合上述两式,可以得到滚珠的变形协调关系,即:
εsi=(εc-εa)-(εd-εb)-εni
(5)
这里(εc-εa)和(εd-εb)分别是第i个球和i-1个球的轴向变形。当第i个滚珠及i-1个滚珠和滚道接触时,相应轴向变形将抵消丝杠的几何误差σisinβicosλ,σi-1sinβi-1cosλ和滚珠接触变形的轴向投影δisinβicosλ和δi-1sinβi-1cosλ,这就是所要研究的位移协调理论。将他们代入式(5),就可以得到考虑误差情况下的变形协调条件:
εsi=[δi-1sinβi-1-δisinβi-
(σi-1sinβi-1-σisinβi)]cosλ-εni
(6)
式(6)就是滚珠在考虑误差情况下变形协调关系。
1.3 滚珠受载模型的建立
本小节根据误差情况下的变形协调条件,建立滚珠受载分布的模型,假设滚珠丝杠副每个滚珠的接触角在每一时刻都相等。根据式(6)可得:
(7)
式(7)中,δi、δi-1是第i个滚珠及i-1个滚珠和滚道接触时,相应接触变形变形量,(σi-1-σi)为误差项。对于间距ΔL内的丝杠轴和螺母在T-C状态下得变形量εni和εsi可以由式(8)和式(9)得到:
(8)
(9)
这里En,Es分别为丝杠和螺母的弹性模量。An,As分别为丝杠和螺母的有效截面区。假设丝杠的导程为L,每个导程内的滚珠数为M,则两个滚珠间的轴向平均距离ΔL为:
(10)
由于主要的接触曲率随着方向变化,而且接触区是一个椭圆,所以形变量δ可以由赫兹弹性接触理论得到:
(11)
这里K为常数,它是由接触点的主曲率半径,材料的弹性系数等决定。
将式(1)、式(8)、式(9)和式(11)代入式(6)中得:
(12)
假设每个滚珠的接触角都相等,则式(12)化为:
(13)
式(13)反映了第i个滚珠及第i-1个滚珠法向接触载荷Pi与Pi-1的关系,其中(σi-1-σi)为误差项,接触角β与螺旋升角λ都是已知的,而其他参数K,εsi,εni都是可以通过上述相应的计算式得出的。
因此,式(2)与式(13)组成了滚珠丝杠副变形协调条件及几何误差下的载荷分布模型,即:
(14)
这个滚珠受载模型可以运用牛顿迭代法计算得到,通过计算出每个滚珠的受载情况,就可以分析出整个滚珠丝杠滚珠的受载分布情况。
此外,上述模型是滚珠丝杠副在丝杠受拉和螺母受压状态时(即T-C状态)的建立分析的。当然,其他外部载荷条件(如假设单螺母和丝杠都承受张力)的非线性方程也可以根据上述的方法构造建立。
2 滚珠受载实例计算与误差分析
2.1 无误差时滚珠受载分析
现就滚珠丝杠副滚珠载荷分布问题,进行了载荷分布的理论计算与推导,举例对某型号滚珠丝杠副的滚珠受载进行计算。各项参数如下:丝杠公称直径d0=16mm,螺母外径Ds=30mm,滚珠直径db=3.175mm,导程L=4mm,滚道曲率半径和滚珠半径之比t=1.04,滚珠圈数n=4,每个滚珠的接触角β0=45°,螺旋升角λ=4.55°,工作滚珠总数Z=52,轴承钢的弹性模量E=2.07×105MPa,泊松比μ=0.29,且给螺母施加30kN的轴向外载荷。
由式(10)得两个滚珠间的轴向平均距离ΔL为:
丝杠和螺母有效截面积为:
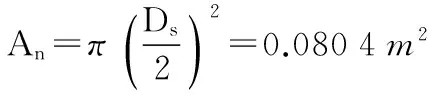

计算K,由查文献[1]可知:
(15)
计算滚珠与滚道面出的曲率和∑ρ
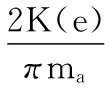
由Kn的值得则式(12)中Kp的值:
当滚珠直径无误差时,式(15)迭代方程中σi-1-σi=0,式(14)模型可变为:
(16)
运用牛顿迭代法计算出每个滚珠的受载情况,求得最大法向接触载荷P1= 0.928kN,最小法向接触载荷P52=0.711kN。以滚珠数为横坐标,第i个滚珠法向载荷Pi与最小载荷P52之比为纵坐标,得到滚珠丝杠副的载荷分布情况。
为了验算本模型计算结果的准确性,以滚珠数i为横坐标,第i个滚珠接触载荷与最小接触载荷之比Pi/Pmin,将本模型在无误差情况的计算结果和半螺距模型[2]进行比较,初始的接触角β0=45°。
在T-C状态的情况下,半导程模型和本文模型的比较结果如图6所示。由图可知,第i个滚珠的接触载荷随着i的增大而呈减小的趋势。而且,本模型滚珠的负载分布曲线介于半螺距模型曲线之中,这表明本模型计算结果与半导程模型结果是吻合的。
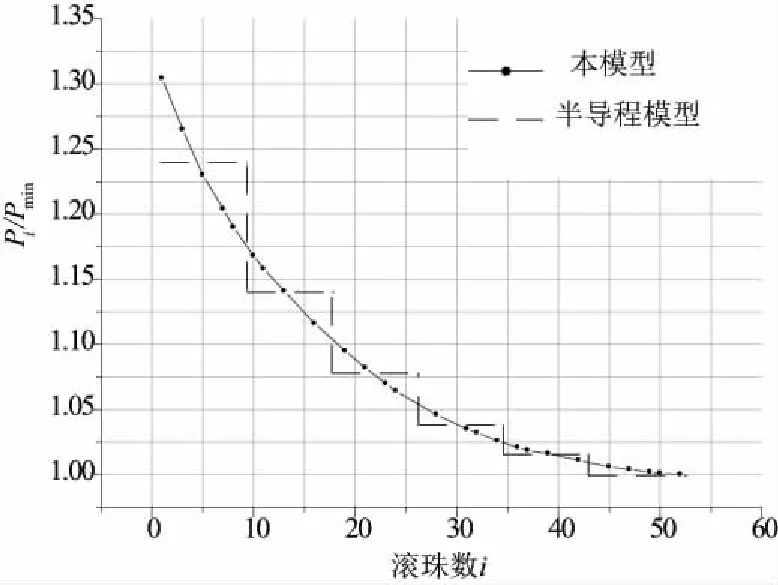
图6 无误差情况下本模型和半螺距模型滚珠载荷分布情况图
2.2 滚珠几何误差对载荷分布的影响
2.2.1 滚珠几何误差的计算分析
图4所示的,滚珠几何误差可以转化成本模型所计算的误差。在本文建立的模型中,滚珠几何误差对载荷分布的影响是可以分析计算的。
丝杠滚珠的直径误差实际上是一种随机误差,很难分析,但是在一定的统计范围内误差对滚珠受载的影响是可以分析的。假设给定一组滚珠的直径误差,如图7所示,该组平均几何误差为-2μm。对于滚珠直径误差的分析,Masaomi Tsutsumi等[6]结合数值实验的结果分析指出,对于一组随机误差的滚珠直径,当误差的平方差Sd≤5μm时,滚珠所受的法向载荷变化量ΔP≤1N(不到1%的变化量)。因此当给定一组误差的平方差Sd≤5μm时,,由于误差随机性引起的载荷变化量可以忽略,可以直接用平均几何误差来代替计算。

图7 负误差情况下滚珠载荷分布情况图
当滚珠平均几何误差为-2μm时,式(15)迭代方程可以转化为:
(17)
这样联立式(17)迭代方程和式(2)即可以求出所有滚珠的接触载荷。
同理可以分析求出滚珠平均几何误差分别为+1μm,+2μm,-4μm时的滚珠受载情况。
2.2.2 误差对滚珠受载的影响分析
现研究误差对滚珠载荷分布的影响。首先,假设位于丝杠中间的第i个滚珠的直径误差是负误差,对于不同的负误差,计算出每个滚珠的接触载荷。我们来研究当误差σi-1-σi=-2um和σi-1-σi=-4um两种负误差情况下的滚珠接触载荷分布情况。首先计算出每个载荷Pi与最小载荷P52之比,然后再画出载荷分布图,载荷分布图如图7所示。由图可知,第i个滚珠的接触载荷呈减小的趋势,减少的量与误差的比例有关。从图中还可以得出结论,滚珠丝杠副工作滚珠中的载荷会随着负误差的增加而增加。
接下来,再研究误差σi-1-σi=+1um和σi-1-σi=+2um两种正误差情况下的滚珠接触载荷分布情况。同样地计算出每个载荷Pi与最小载荷P52之比,画出载荷分布图,载荷分布图如图8所示。从图中可以得出结论,滚珠丝杠副工作滚珠的载荷随着正误差的增加而减少。
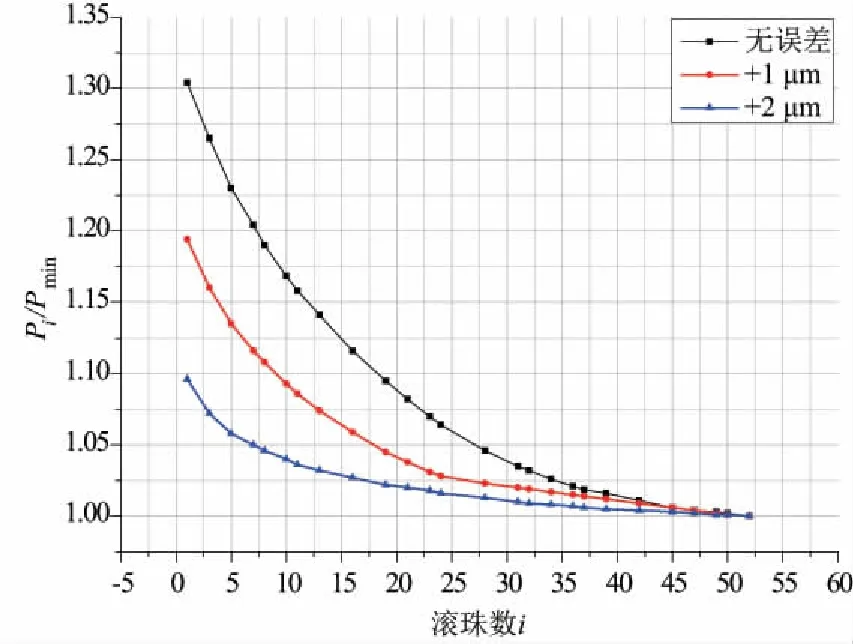
图8 正误差情况下滚珠载荷分布情况图
3 结论
根据以上丝杠几何误差对滚珠丝杠载荷分布影响的分析,可以得出以下结论:
1) 本文提出的滚珠丝杠机构载荷分布计算模型可以用来计算滚珠几何误差在一定分布规律内的滚珠载荷。
2) 接触位置的负误差会导致滚珠在该位置的赫兹接触载荷的减小,正误差会导致载荷的增加,增加量和减小量与丝杠其他滚珠共同分担。
3) 上述中一些运用于单螺母结构的结论也适用于双螺母结构。
[1] T.A.Harris,滚动轴承分析[M](1、2卷),北京:机械工业出版社,1967.
[2] M. Izawa, H. Shimoda, Study on the load distribution in the ball screw,Japan Journal of Precision Machine 42 (11) (1976) 1021-1028.
[3] 程光仁,施祖康,张超鹏.滚珠螺旋传动基础[M].北京:机械工业出版社,1987.
[4] 万长森.滚动轴承的分析方法[M]. 北京:机械工业出版社,1987.
[5] 饶振纲,王勇卫.滚珠丝杆副及自锁装置[M].北京:国防工业出版社,1990.
[6] Masaomi Tsutsumi, Xuesong Mei, Study on the load distribution of ball screws with errors, Mechanism and Machine Th- -eory 38 (2003) 1257-1269.
Research on Load Distribution of Ball Screw
ZHANG Chen-ling,FAN Yuan-xun
(College of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)
The stress of the ball is complicated when the ball screw is loaded by external force.However, the ball load is analyzed simply according to the average load distribution when its load distribution is researched on. This is large different from the actual load distribution. A model is developed to analyze its load distribution and geometry errors which have influence on its load disfribution.
ball screw; load distribution; geometry errors
张陈灵(1988-),男,江苏南通人,硕士研究生,研究方向为机械电子工程。
TH133.2
A
1671-5276(2014)02-0006-04
2013-01-17

