基于 A*算法与自适应分片的大规模最优路径规划

郭耕辰 冯良炳 邓 亮 赵永刚 刘 宇

(中国科学院深圳先进技术研究院 深圳 518055)

基于 A*算法与自适应分片的大规模最优路径规划

郭耕辰 冯良炳 邓 亮 赵永刚 刘 宇

(中国科学院深圳先进技术研究院 深圳 518055)

路径规划引擎是在线地图系统中一个至关重要的部分，静态路径规划算法是重中之重。现有的对 A* 算法的改进主要是通过预处理算法，对路网数据进行静态分层预处理，其效率过低。文章提出了一种自适应分层的思想，同时对 A* 算法的启发式函数进行改进，引入了方向引导函数，使得 A* 算法在日常路网上的可用性有了较大的提高。实际的路网实验表明，提出的算法的搜索效率、效果均优于同类算法，与标准层次 A* 算法相比，文章算法的搜索空间降低为原来的 42%，搜索时间仅为原来的13%。

路径规划；A* 算法；自适应分层；方向启发式函数

1 引 言

对于一个在线地图系统来说，路径规划引擎是其中一个重要的组成部分。路径规划问题，简而言之就是以路网拓扑结构为基础，在其形成的有向图中找到一个最短路径的问题。在现实环境中，往往指的是从出发点到目标点总代价最小的路径过程。这个代价依据相应的需求来制定，如道路的物理长度、道路的类别和车速限制等。

A* 算法在进行大规模搜索的时候，耗时急速增加，因此，在应用到实际的系统中时，需要对其进行优化。优化可以在如下几个方面进行：缩小搜索空间、双向搜索和层次化搜索。钱红昇等[1]提出了一种在分层基础上对启发式函数的改进，在前期搜索过程中，由于运算速度的要求较高，可以通过增大权值来加大启发式函数的作用。在后期过程中，路径搜索主要以精度为重，可以减小启发式函数的权重以提高搜索精度，同时，设置了权值的上下限阈值，以保证不会因为前期搜索太快而损失搜索精度，后期因为搜索太细而损失了搜索速度。这种改进的 A* 算法综合考虑了路径搜索效率和搜索精度的双重要求，在保证搜索精度的同时提高了搜索效率。实验结果表明其总的搜索节点数明显小于经典 A* 算法，效率有了较大的提升。在实际工程基础上，往往使用双向搜索[2]来加快寻路的速度。双向搜索是指从起点和终点同时运行路径规划算法，当发现有候选点满足终止条件后，终止算法。殷[3]和Bauer 等[6]提出了路径搜索过程中，起点和终点所在方位对缩小搜索空间的重要性，通过设置优先区域，在优先区域内搜索，减少了无意义的运算。但其设计的启发式函数时间复杂度比较高。Holzer 等[4]则提出了工程化的分层思想用于优化路网图，但无法自动适应不同路网的结构，无法动态的对层次进行改变。很多优化的思想在算法之间是可以通用的，Delling 等[5]提出了很多工程化的优化方式，穆[7]从数据结构层面上，引入了Cheap 表来改进 open 表的操作效率，用时间换取空间，但这两者之间的平衡很难把握。

本文将在现有 A* 算法的改进基础上，提出一种针对方向加强的启发式函数，待搜索路径偏离起点和终点向量越远，导致代价越高，因此算法会尽量选出与出发点到目的地方向相符度高的候选点，极大地缩小了搜索空间。同时提出一种自适应的分层方式，使得算法对路网的动态适应成为可能，从而达到对现有路径规划方法的优化。

2 算法描述及实现

2.1 A* 算法

A* 算法[8]是人工智能中的一种启发式算法，它通过定义代价函数评估代价大小来确定最优路径。代价函数为：

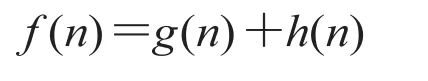
其中，n 表示待拓展的节点；g(n)表示从起点沿着已生成的路径到一个给定节点的移动开销，这个值由我们根据路网选定的度量来决定，一般情况下，取道路的物理长度；h(n)表示从给定节点到目的节点的估计移动开销，这个值是一个启发式的预估。

现有的启发式函数最主要是如下几种：(1)以起点和终点在标准坐标系上的绝对轴距总和的曼哈顿距离；(2)在二维空间中两点之间的直线段距离的欧氏距离；(3)在二维空间下取起点和终点坐标数值差的最大值的切比雪夫距离。

以上的三种启发式函数主要应用于平面网格，在城市路网的应用方面，适用性不强，因此本文首先会对启发式函数进行优化。

同时，上述的 A* 算法如果直接应用在大规模路网上将会产生严重的计算性能瓶颈。现有的效率较高的算法[1]往往是对路网进行分层处理，降低路网的复杂性。本文将通过在分层基础上，加上自适应的划分过程，进一步提高算法的效率。

2.2 启发式函数

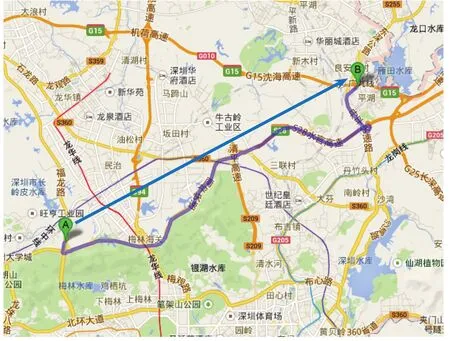
图 1 方向导向实例Fig. 1. Goal-directed example

如图 1 所示，根据路网图的特点，从起点到终点的路径，其方向上应符合从起点指向终点的向量[6]，也就是每次在路径选择上，与 AB 向量夹角越小的边，其权重就越大。记起点为终点为则该向量与坐标轴 x 轴正方向的夹角为待搜索点的坐标为与坐标轴 x 轴正方向的夹角为则向量 SB 与向量 AB 的夹角为但是，在实际计算中使用这个公式，会导致计算量过大，路径规划过程的大部分运算时间都被用来计算这个启发式函数。因此，为了表示待搜索点与待搜索路径结果的符合程度，同时还能放大这种差异，本文选用图 2 中，以点 S 分别向 x 轴正方向和 y 轴正方向做延伸，与三角形的两条边相交于两个点，形成的矩形面积(即 S 点形成的梯形与完全符合AB 方向形成的三角形的面积差)作为启发式函数(公式(1))来引导路径规划过程。

图 2 启发式函数Fig. 2. Heuristic function

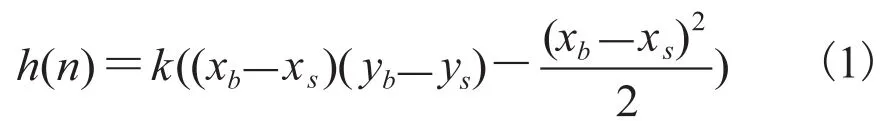
其中 k 表示放大系数，用来调校向量的大小，根据每个系统的实际情况进行取值，用来改变这种方向引导对整个路径选取过程的影响系数。

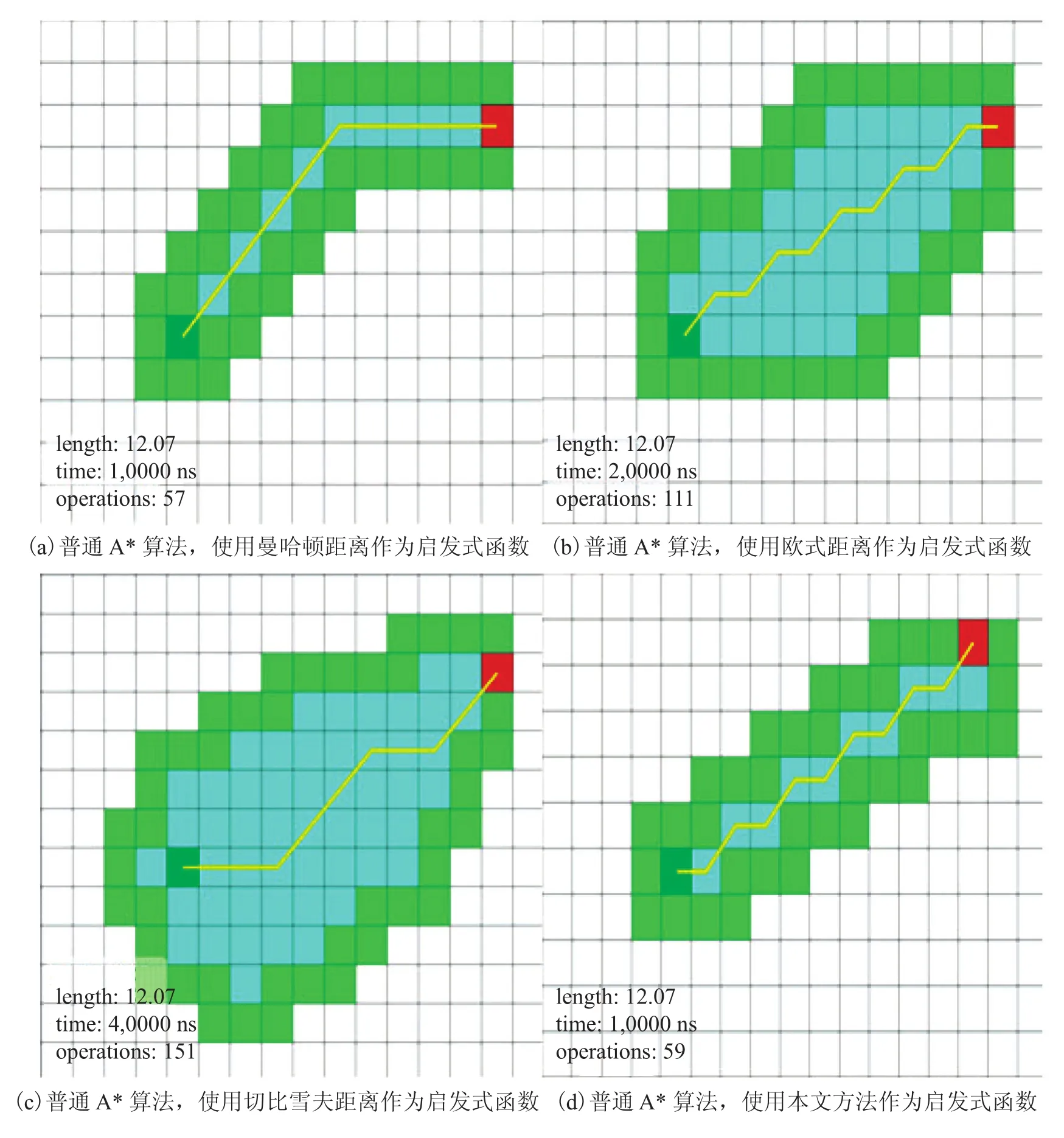
图 3 使用普通 A* 算法测试各启发式函数的搜索空间Fig. 3. The search space for each heuristic function used common A* algorithm testing

图 3 为常见 A* 启发式函数，图中(a)～(d)分别为使用曼哈顿距离、欧氏距离、切比雪夫距离和使用本文的强化方向指向距离的搜索空间的测试结果。

双向策略[2]同时进行正向搜索和反向搜索两套搜索，当发现一个点同时被正向搜索和反向搜索选为路径点的时候，算法结束。从图 4 可以看到，使用双向搜索的时候，搜索空间的优化效果更为明显。

图 4 使用双向 A* 算法测试各启发式函数的搜索空间Fig. 4. The search space for each heuristic function used bi-direction A* algorithm testing

2.3 自适应分层

对实际的大规模路网进行搜索时，如果直接使用上述改进的 A* 算法，时间代价太大。一般都采用对路网图进行层次划分方法，层次划分可以通过动态和静态两种方式进行。Holzer 等[4]提出的代表性静态方式通过对路网划分为网格，对给定的路网图赋予相应的网格结构来实现。本文将引入一种动态的分割方法，可以对整个地图程序的路径规划引擎提供自适应的分层，以此来减少人工的参与和对各种不同地区的路网结构进行适配。

路网的分层通过构建一系列的层次图来实现。一个路网 G 的层次图实质上通过以下两种方式拓展了原有的 G 图：

(1)通过层次结构中添加的边拓展了 G 的边集 E；

(2)V 集中任意两点 s、t 的最短距离与层次图 M 中 s 到 t 的距离相等。

为了得到以上的层次图，我们使用了一种叫做组件树[4]的特殊数据结构来实现。生成层次图M 的目的在于使每个层次的子图要比原有的路网图 G 规模小。这样，把 A* 算法应用到这个相对小的图上，速度会更快一些。

层次图 M 通过以下输入来构建：

我们把 Li＝(Ei, Ui, Di)叫做多层图 M 的第i层。同时我们预先定义 L0＝(E, Ø, Ø)为第 0 层，其中 E 表示原路网图 G。加上第 0 层，我们说M(G , S1, …, Sl)是一个 l+1 层的图。

层次图的构建是一个迭代的过程，我们总是假设已经构建了第 Li—1层。迭代从 i＝1 开始，对于 Si—1中的每个点 u 来说，以 u 为根在图(Si—1, Ei—1)中构建一个最小路径树 Tu。具体判断一个候选边(u, v)是否被添加到集合Ei，Ui，Di的条件为：

Li包含了一个边(u, v)当且仅当没有 Ti中 u到 v 路径上的点属于 Si。

换句话说，如果 u 到 v 路径上的点除了两个端点 u 和 v 之外，在 Si中再也找不到其他的点，此时边(u, v)被添加到 Li中去。新边(u, v)的权重为 G 中 u 到 v 的最短路径长度。

值得注意的是，层次 Li在这个构建的过程中不是唯一的，因为最短路径树不是唯一的。到此为止，我们可以给出多层图的定义：

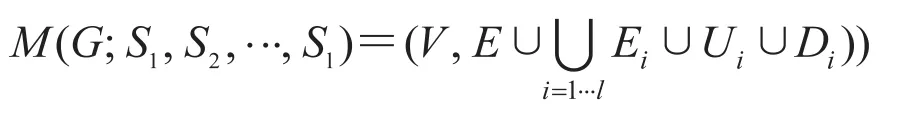
图 5 是一个三层图的例子，第 0 层包含了原始的路网图 G。取 S1＝{a, b, c}，S2＝{a, c}。为了更好的说明问题，我们在第 1 层和第 2 层上画上了所有点，但实际上，他们是不存在的。第 1层和第 2 层被化成了两个平面，上面的平面用于表示边集 Ei，下面的平面用于表示图 G～Si中的连接组件。Ui和 Di中的边连接了一个层的不同平面。

图 6 是与图 5 对应的组件树，只有点 s 和 t的叶子节点被保留。

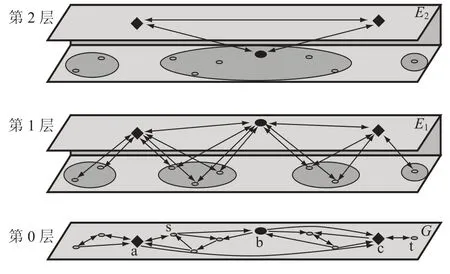
图 5 三层图例子Fig. 5. A three levels example

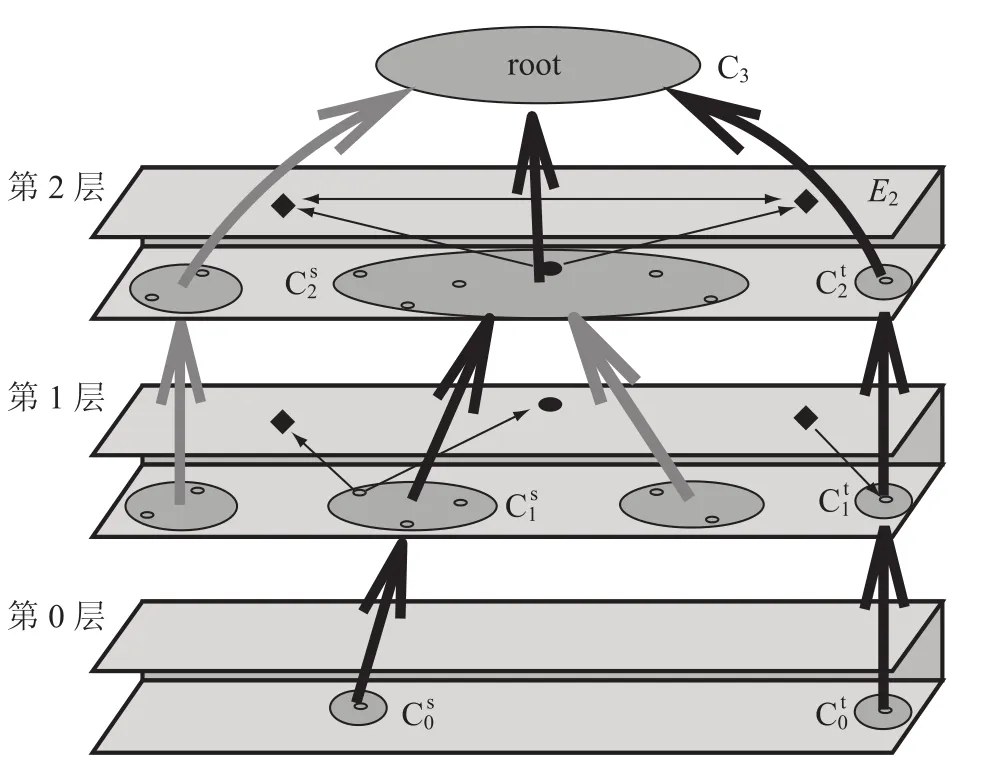
图 6 对应的组件树Fig. 6. A corresponding component tree

由于最短路径树不是唯一的，路网的这个预处理过程就涉及到图的分割问题，如果仅仅使用网格来分割这个图，不能最大程度地反映出路网的自然属性。实际上，路网不同部分的性质差别很大，人口密集区域应该分割得更细，而如湖泊等地点的分割粒度要求比较粗，因为没有人会去试图寻找从湖泊中央到湖泊边界的路径，这也不是路径规划系统的应用范畴，因此，本文提出了自适应分割的概念。

自适应分割，就是在原有的路网网格分割基础上，对内部查询频繁的单位格进行进一步自适应划分，使得查询频繁的区域(即人口密集区域)的划分粒度更细致，提高查询的效率。

首先，按照网格分割的思想，假定要将路网划分为 n 层，最开始为第 n 层，对整个原路网图G 以坐标为标准进行 Kn等分；然后第 n—1 层，对第 n 层划分后的格子进行 Kn—1等分，并将这个过程一直迭代下去，直到第 1 层为止。这个过程被叫做路网的预处理过程，其耗费的时间比较长，但是往往在很长的一段时间里，在路网整体结构变化不大的情况下，不需要多次运行。这个过程与路网代价的选取是相互独立的。

图 7 对层次化优化原理进行了进一步说明。如果路径 BC 和路径 CD 在第 i 层被分到不同的格子里面，这样在层次结构的表示上，第 i+ 1 层里面，就会保存一个从 B 到 D 的快捷方式(shortcut)，在第 i+1 层的搜索过程中，如果一个人找从 A 到 D 的路径，就可以得到 A→B→D的结果，然后在下一层对 BD 这个 shortcut 进行展开，其路径查找次数就会降低。

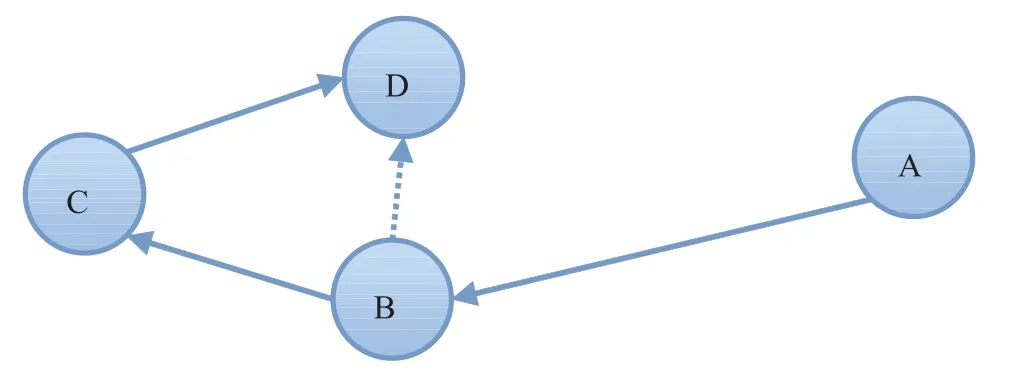
图 7 层次化优化的说明Fig. 7. The hierarchical optimization

这便是分层的好处，也是本文要引入自适应分割对层次进行扩充的目的。

如果系统运行过程中，很多用户去查找一个格子中的起点和终点，则说明在这个格子里，路网节点的密集程度比较高，也可理解为人口密集程度比较高。因此，如果对这个格子进行进一步的划分，可以得到一个更好的层次结构，从而提高系统的查询效率。而且在预处理过程后，网格的结构已经基本形成，往往这个自适应的过程并不会对原有的层次结构产生过大的改变。同时这种新的分割与代价的选取是相关的，可以根据不同的代价，如道路的长度、道路的限速等动态而灵活改变。

自适应扩充的过程如下：

在整个系统中，为第 1 层(该层是分割粒度最小的一个层)每个格子维护一个计数器，设定一个阈值 T1，每发生一次格子内的查询，计数器 c 加 1，当达到 c＞T 的时候，对该格子进行分割。类似于细胞增殖的过程，当其需要向下一代繁衍的时候，对这个格子的所有结构，包括上下文等信息复制 K1份，新产生的 K1个格子与原格子不同点在于其计数器置 0，同时，格子的面积是原来的 K1分之一。原格子在第一层被标记为不可用。但这种裂变并不是无止境进行下去的。分层之所以不可以无限划分，是因为要调和连通性和划分粒度之间的矛盾，如果划分过多的话，会导致附加的存储信息过多，干扰查找的效率。因此，在系统的实现过程中，若第一层的原格子被标记为不可用之后，其计数器的值将用来表示其内部分裂的次数，当分裂次数达到系统设定的阈值 T2的时候，分裂不再发生。

2.4 算法实现

给定路径规划的起点 S 和终点 D，使用本文的方法求最短路径的步骤如下：

(1)加载路网数据，对路网数据进行初始化，本文选用以网格方式对路网进行划分。

(2)从路网的类金字塔的层次图中，从高层向底层查找，直到找到第一个使 Si和 Di不在同一个格子的层次 L，如果 L＞0，则直接调用本文的指向性 A* 算法来计算最短路径，用 Si和 Di的坐标算出方向向量，使用启发式公式(1)作为常规 A* 算法[8]的 h(n)。如果 L＝0，说明可能需要自适应分层，找到 Si和 Di所在的格子，由 2.3 中所述的条件判断该格子是否可以分割。如果可以分割，产生新格子，再调用本文的指向性 A* 算法；如果不可以分割，则说明裂变次数已经达到上限，直接调用本文的指向性 A* 算法得到规划结果。

(3)如果(2)中得到的路径 P1是从层次 0 得到的，则 P＝P1直接跳转到(5)，如果是从其他层次得到的，遍历路径结果，找到低层路网到高层路网最近的节点作为新的起点和终点，分别记为 S' 和 D'，调用本文的指向性 A* 算法求 S 到 S'的路径为 P2，D 到 D' 的路径为 P3。

(4)组合路径 P＝P1+P2+P3，得到最终的路径，跳转到(5)。

(5)返回最终结果 P，即为 S 到 D 的最短路径。

3 仿真实验与结果分析

从图 3 的网格实验结果可以看出，使用欧氏距离作为启发式函数和本文的方向指向函数得到的路径结果是最正确的，因为在无障碍的情况下，两点间线段最短。因此取本文启发式函数与欧氏距离做启发式函数作对比。如表 1 所示，相比之下本文启发函数的时间仅需要 1 ms，比欧氏距离作为启发式函数快一倍，搜索空间也仅为欧氏距离作为启发式函数结果的 53%，效率提升非常明显。

以上结果的放大系数 K 取值为 1，实验过程表明，K 越大，算法的贪心性也就越强，如果过强的话，在实际路网中会对结果的正确性造成干扰。例如，一个完全符合起点和终点向量方向的道路，其代价为 α，另一条稍微偏离一点的道路的代价为 β，αβ，K 的值如果设定过大的话，往往会导致最终选取了第一条道路。

因此 K 的选取要结合路网的比例尺、度量的表示单位等数据来选取。一般选取 K 为单位代价的坐标偏移值。例如，如果每个格子的代价为1，坐标的偏移也为 1，那么取 K＝1。

图 4 是双向路径规划试验的结果。本文启发式函数的搜索空间也仅为欧氏距离作为启发式函数结果的 69%。

为了验证此算法在真实路网上的优化效果，采用深圳路网图的一部分作为测试集。分别对经典 Dijkstra 算法、经典层次 A* 算法、自适应层次A* 算法和指向性自适应层次 A* 算法进行比较。

表 1 网格模拟结果Table 1. Grid simulation results

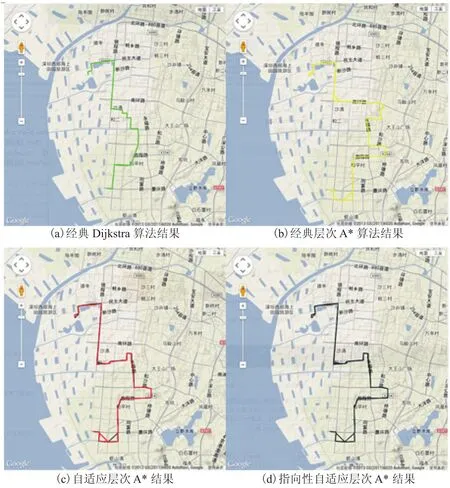
图 8 路网实验结果Fig. 8. The experimental results of road network

我们使用的测试环境是深圳市路网图，共有 30256 个节点和 185202 条路段，运行在 Intel 2.0 GHz 主频的 CPU 上，内存为 2G，使用 Java语言开发，使用 SWT 构建桌面环境，以实际的行驶道路长度作为度量参数。仿真结果如图 8 所示。同时从表 2 我们可以看到 Dijkstra 算法虽然得到了最优的路径长度 6957.85 m，但是其搜索时间 4187 ms 要远大于 A* 系列算法。

表 2 路网实验结果Table 2. The network experimental results

同时在 A* 算法中，本文的指向性自适应层次 A* 算法在裂变前的路网结构与经典层次 A* 算法的路网结构是相同的，所以两者结果相同。但查询若干次后，第 1 层的高层路网发生了裂变，由于此时高层对搜索时间的影响比较大，使得搜索时间由 1710 ms 降为 1582 ms，但是搜索的节点数反而增加了，由 3583 个节点增加到 3894，这是由于搜索底层节点到高层节点时，多搜索了一些节点。

在自适应层次 A* 算法上加上指向性启发式函数后，搜索空间从 3583 降低到了 1545，降低为原来的 43%，可见，指向性启发式函数对搜索空间的缩小作用很大，使得搜索时间也大幅降低为 281 ms。值得注意的是，带指向性启发式函数的算法裂变后，它的搜索节点数降低了，而非指向性的实验结果则是增加，这是由于在计算底层节点到高层节点的过程中，由于是在同格子的一个很小的区域中进行，因此，指向性启发式函数对搜索空间的缩小更为明显。

综合以上分析，搜索节点的减少得益于启发式函数对方向的引入，同时，自适应分层技术通过对层次进行扩充来提高搜索的效率。虽然不排除损失了一部分精度，但指向性自适应层次 A* 算法算出来的结果已经很大程度上接近于Dijkstra 算法的结果。这更加符合路径规划引擎对路径规划算法的要求。

4 结 论

本文在常规 A* 网格分层的基础上，提出了一种自适应的层次划分方法，根据算法运行时的情况对层次进行动态扩充，顾及到了划分粒度和层次连通性对效率影响之间相互的平衡。同时结合指向性的启发式函数，极大地缩小了搜索空间，提高了搜索的效率，且算法的精度和效率也达到了一个比较好的平衡。实验结果表明，改进后的 A* 算法的效率比原有的经典层次 A* 算法高 8 倍以上，适用于实际的路网环境。

[1] 钱红昇, 葛文锋, 钟鸣, 等. 基于分层的改进 A*算法在路径规划中的应用 [J/OL]. 计算机工程与应用, 2013.

[2] 李引珍, 顾守淮. 有向网络上两顶点间最短路径的双向搜索算法 [J]. 甘肃科学学报, 1998, 10(2): 11-14.

[3] 殷超. 基于改进 Dijkstra 算法的最短路径搜索仿真 [J]. 山东理工大学学报(自然科学版), 2010, 24(6): 33-36.

[4] Holzer M, Schulz F, Wagner D. Engineering multilevel overlay graphs for shortest-path queries [J]. Journal of Experimental Algorithmics, 2008, 13: 2.5-2.26. doi: 10.1145/1412228.1412239.

[5] Delling D, Sanders P, Schultes D, et al. Engineering Route Planning Algorithms [M]. Springer Berlin Heidelberg, 2009: 117-139.

[6] Bauer R, Delling D, Sanders P, et al. Combining Hierarchical and Goal-directed Speed-up Techniques for Dijkstra’s Algorithm [M]. Springer Berlin Heidelberg, 2008: 303-318.

[7] 穆中林, 鲁艺, 任波, 等. 基于改进 A′ 算法的无人机航路规划方法研究 [J]. 弹箭与制导学报, 2007, 27(1): 297-300.

[8] Hart PE, Nilsson NJ, Raphael B. A formal basis for the heuristic determination of minimum cost paths [J]. IEEE Transactions on Systems Science and Cybernetics, 1968, 4(2): 100-107.

Large Scale Route Planning A＊ Algorithm Based on Self-Adaptive
Hierarchy Method

GUO Gengchen FENG Liangbing DENG Liang ZHAO Yonggang LIU Yu
( Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055, China )

The route planning engine has already become an important part for an online map system. The route planning algorithm is the key for the engine. The existing improvements for A* algorithm are mainly on the preprocessing part in which the roadmap data were layered statically. In this paper, an adaptive hierarchical method was proposed with an improved heuristic function which has goal-direction process. It greatly improves the efficiency and usability of A* algorithm in the engineering road planning system. The experiment result shows that the algorithm takes up only 42% of the search space and 13% of the search time when compared with the general A* algorithm.

route planning; A* algorithm; self-adaptive hierarchy method; directional guiding heuristic function

TG 156

A

2013-12-29

国家自然科学基金项目(61070147)，深圳市科技研发资金基础研究计划(JC201105190951A)。

郭耕辰，硕士，研究方向为地理信息系统和图形图像；冯良炳(通讯作者)，博士，研究方向为智能计算与智能控制、多视角三维重建、网络服务组合和增强现实，E-mai：lb.feng@siat.ac.cn；邓亮，硕士，研究方向为模式识别和视频监控等；赵永刚，硕士，研究方向为增强现实和图像处理等；刘宇，硕士研究生，研究方向为图像检索和软件架构。