一种基于光学定位的自由式三维超声系统研发

温铁祥秦文健辜 嘉

1(中国科学院深圳先进技术研究院 深圳 518055)

2(中国科学院大学 北京 100049)

一种基于光学定位的自由式三维超声系统研发

温铁祥1,2秦文健1辜 嘉1

1(中国科学院深圳先进技术研究院 深圳 518055)

2(中国科学院大学 北京 100049)

自由式三维超声成像是一种新型的采用二维超声原理进行任意部位三维成像的设备，可以在传统的二维超声探头上固定用于空间定位的标记物，对扫描对象进行任意部位、大范围的三维扫描成像。文章介绍了一种可应用于微创手术导航的自由式三维超声成像系统，并详细分析了当前基于距离加权的三维超声重建算法的性能和优缺点。通过对体模和动物器官的超声图像扫描，并使用三维重建系统分别进行超声三维重建，得出了比较满意的结果，验证了三维重建算法及三维重建系统的可行性和有效性。

超声图像；三维重建；距离加权插值算法；体绘制

1 引 言

在过去几十年里，图像引导在手术治疗方面的应用越来越广泛，而三维超声的使用不仅安全，且图像显示直观，能准确定位病变组织，缩短医生诊断时间[1]。近年来，涌现出了各种三维超声成像系统，但最常用的还是在常规的二维超声设备上附加定位装置的自由式三维超声系统。它使用二维超声图像及其相对位置关系来重建出三维图像。

三维超声重建的一个关键步骤是体数据的重建[2]。重建算法的选择很重要，因为它既需要保存超声图像的细节信息，又要求降低图像的斑点噪声。当前，自由式三维超声重建算法主要有三大类，分别为：基于最邻近体素的算法(Voxel Nearest Neighbor，VNN)，基于最邻近像素的算法(Pixel Nearest Neighbor，PNN)和基于距离加权的算法(Distance Weighted，DW)[2]。一般地，在降低噪声和减小阴影方面，DW 算法比VNN 和 PNN 算法表现得好。除了以上经典的算法外，2003 年，Jose-Estcpar 等[3]提出了一种基于自适应高斯核的插值算法；2004 年，Penney等[4]运用非刚性配准实现了三维超声体数据的重建；2005 年，Coupe 等[5]提出了基于探测器轨迹的三维自由臂超声重建方法。与经典的算法相比，后面几种算法对图像质量有一定的改进，但是这些算法的效率低、耗时长，实验结果表明并不能满足微创手术的实时性要求。因此，本系统采用具有较快重建速度的 DW 算法，同时又能够获得较理想的重建图像质量。

本文研究内容是研发一个自由式超声图像三维重建系统，在 Windows 操作系统下，利用Visual Studio 2005 开发工具，结合 VTK 可视化技术构建出一个完整的交互式超声图像三维重建处理平台。在 2D 超声探头的定位方面，本研究采用 NDI 光学定位系统，自制超声探头定位架。同时系统地研究和分析了自由式三维超声成像系统的体数据重建算法，对基于距离加权插值算法做了一定的改进，在保证重建质量的前提下，提高重建算法的速度，实现自由式三维超声成像系统的数据处理及显示。这一算法可应用于图像引导手术机器人中，在手术过程对医生的手术引导和规划起一定的辅助作用。

本文第二部分将从 3D 超声重建系统的实验装置入手，详细描述超声三维重建的过程；第三部分介绍各种基于距离加权算法及其内在机理，最后对各种算法的效果做对比和分析；第四部分是对超声图像三维重建实验分析研究，最后做了总结。

2 方 法

2.1 实验装置

由于三维超声成像系统需要采集每个二维超声平面的同步位置信息，我们采用蓝韵公司提供的彩色超声设备来采集超声图像。NDI(Northern Digital Incorporated)光学定位系统能得到每个超声平面的位置与方向信息，并计算出每个超声图像上的像素的三维空间位置。系统装置如图 1所示。

图 1 自由像系统组成Fig. 1. System setup for our freehand 3D ultrasound imaging

2.2 三维超声的重建过程

三维超声重建过程一般有三个必要的组成部分：数据采集、三维体数据重建和三维可视化[2,6]，如图 2 所示。

图 2 三维重建的过程Fig. 2. Workflow for the volume reconstruction

2.2.1 数据采集

进行三维成像首先要取得足够的二维数据。绝大多数的三维超声成像系统使用二维超声探头获取一序列二维超声断层图像并经重建完成三维成像过程[7]，不同的只是确定这些二维图像在三维体数据空间位置的方法。本文利用 NDI 光学定位装置进行超声探头的自由式扫描来采集数据。扫描的时候尽可能地平稳和缓慢，这个过程能得到具有空间位置信息的二维超声序列图像。

2.2.2 体数据重建

取得序列二维数据后，便要开始三维重建。三维重建过程中采用的算法根据重建目的的不同而各不相同。如果重建目的是为了三维测量，那么三维重建过程就是从原始二维图像中重建考察目标的表面信息，主要目标在各二维断层图像的边缘；如果三维重建的目的是为了观察脏器的立体形态，那么三维重建过程就是从原始二维图像中重建规则体数据[8,9]。我们的目的是为了手术过程中图像引导，所以三维重建过程主要是要重建出规则的体数据。

三维重建的对象和目的不同，则重建的步骤和具体实现过程也不尽相同。一般来说，重建步骤包括像素重采样和空隙填补两部分[8,10]。

(1)像素重采用

这个阶段主要工作是遍历二维超声平面上的每一个像素点，并根据它们的位置信息，把像素值映射到三维体素中，如图 3 所示。如果不止一个像素同时落入到同一个体素中，就取它们的平均值。这个过程计算的速度很快，不可避免的在规则体数据中留下空隙，故后续工作需要填补空隙[11,12]。

图 3 像素重采用示意图Fig. 3. Illustration of freehand 3D scanning

(2)空隙填补

针对空隙进行插值的方法很多，但基本原理都是利用周围已知的像素值去插值出体素网格中未知的体素值[6]。本文采用基于距离加权的插值算法进行空隙填补。

2.3 距离加权算法[2]

图 4 是基于距离权重插值算法的平面示意图。确定一个半径为 R 的球形邻域，中心点是体素，用落入球形区域的二维超声图像平面上的像素的距离加权平均得出该体素，其中需要确定的参数是加权函数和邻域区间的大小和形状。

传统的距离加权插值方法表达式如下所示：

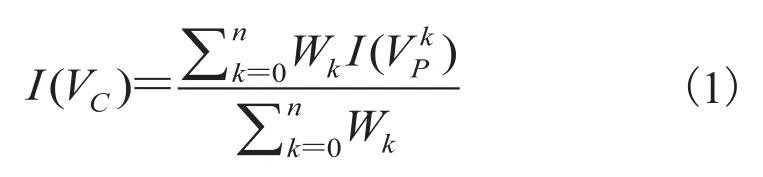
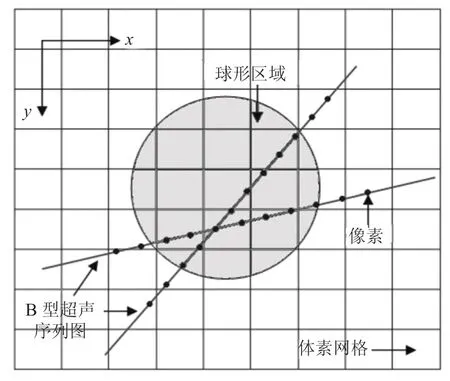
图 4 DW 插值算法的体数据重建示意图Fig. 4. Illustration for the volume reconstruction based on the DW interpolation method

其中，I(VC)是体空间 C 处的体素值，确定以体素 VC为中心的球形区域，n 为落入这一区域内的像素数目。是像素点处的像素值。是第 k 个像素点的权重值，dk是第 k 个像素点到中心体素 VC点的距离。

为了减小以上提到的传统 DW 插值算法的模糊性，提高精度并对超声图像中斑点噪声起到抑制作用，使用平方距离加权(Squared Distance Weighted，SDW)来计算目标像素的值[13]：

Huang 等[6]提出了一种改进的 SDW(HSDW)重建方法，这种方法的表达式为如下的权重函数：

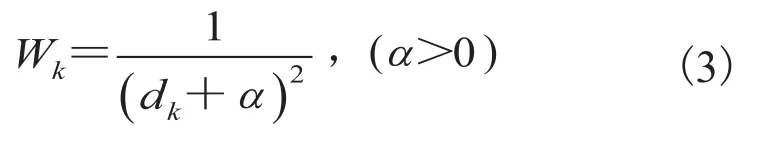
a是调整插值效果的一个正数。因为 HSDW能够对权值提供一个非线性的分配，所以重建体阵列相比于传统的 DW 方法模糊性要低。实验结果表明：当a较大时，能够较好的抑制斑点噪声；当a较小时，能够较好的保存细节信息。因此，在 HSDW 算法中存在噪声较少和细节保存的平衡问题。

为了在保持边缘的同时更好的抑制斑点噪声，Huang 等[6]提出了一种自适应策略来调整SDW方法中的a。这种新的方法利用这一球形区域内像素的统计特性来自适应地控制值a。在三维超声体数据重建中，有 3 个目的：减少斑点噪声、加强组织边界和减少伪影。在 SDW 算法中，较小的a能够很好的保持边缘，但仍然存在很多的斑点噪声；较大的a虽然大大减少了斑点噪声，但令边缘和细节变得模糊。因此，我们的目的就是设计一种改进重建方法，使其能够在保持组织边缘的同时减少斑点噪声。

对于超声图像中斑点噪声，有人提出了一种信号依赖噪声模型(Signal-Dependent Noise Model)：其中 y 为观察到的超声信号，s 为自由噪声信号，n 是噪声[14]。在均匀区域内，假设 s 是一个常数。因此，这一区域内的方差与噪声方差是线性关系：如果这一区域内的算术均值 μ 是 s 的数学期望，那么上式也可表示为：如果在这一均匀区域内只有斑点噪声，即意味着方差和均值是成比例的。

根据这一模型，包含组织边缘的区域

的值相对较大。为了保持边缘，在 SDW 中的参数应该尽可能小。然而，如果这一球形区域是均匀的，参数a应尽可能大。因此设计一种自适应的方法来控制a的值，这种新的自适应平均距离加权插值方法(ASDW))可表示为[6]：

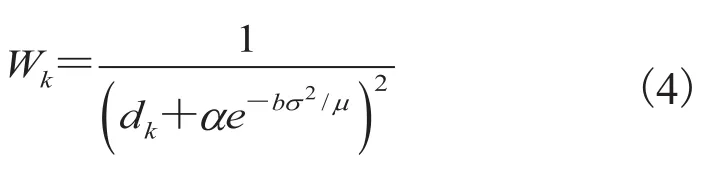
2.4 算法实现

图 5 为三维重建的实现流程图，各插值算法需要分别实现。

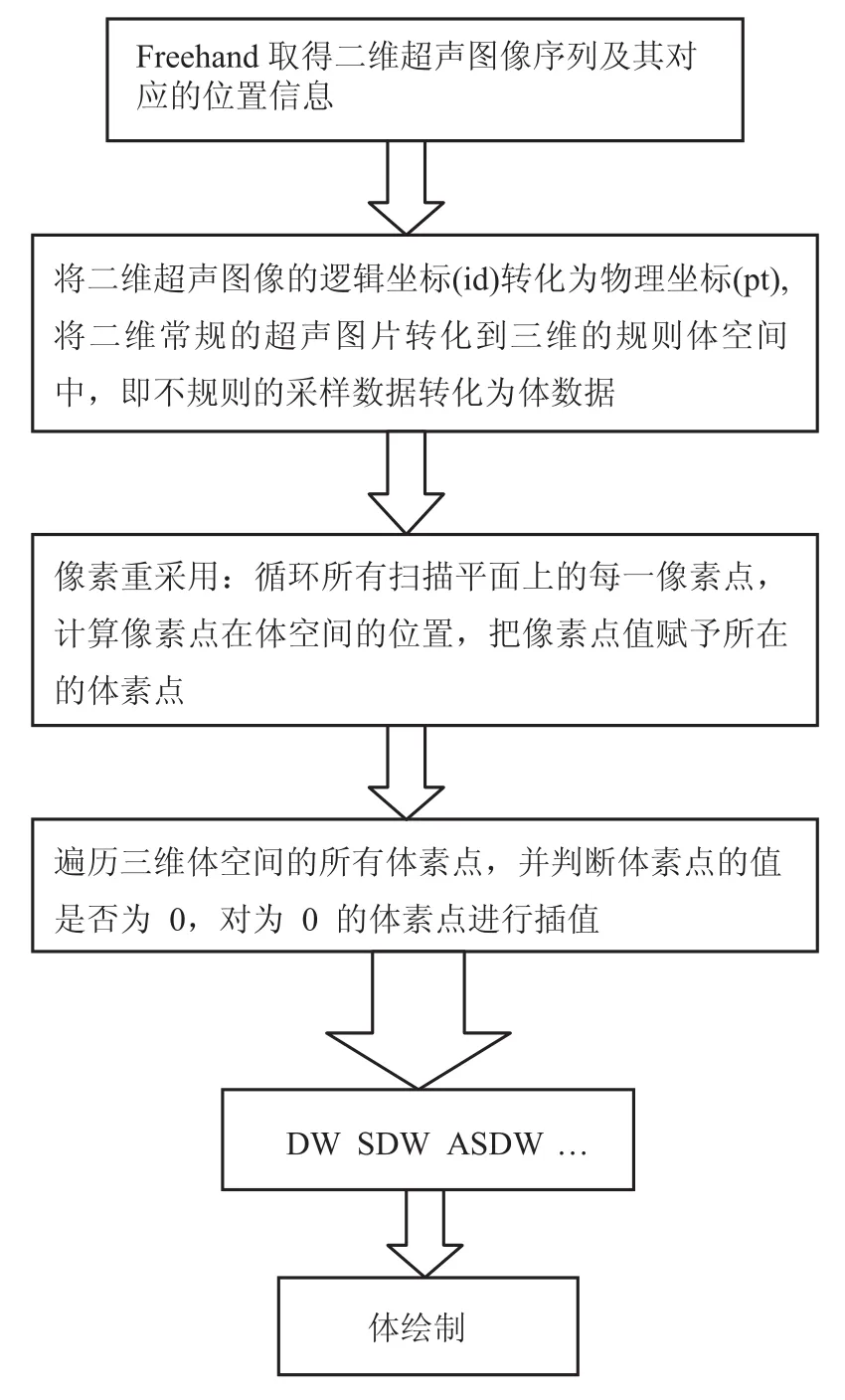
图 5 超声三维重建流程图Fig. 5. Workflow for the 3D ultrasound reconstruction

3 实验结果

我们用 MPFCP x结合xy VTKxp 分别实现了 DW、yyxpxpx2 SDW、PHzSDxW、ASDx2Wx 2插值算法。并且运用体模进行实y验验xx证px。x

图 6 为体模2及其实验环境。为了便于标识，xx体模上部y由y一个斜三角形和一个平行四边形组x成，体模的下部内嵌一个空心管道。扫描时，将体y模放置于水箱内，通过缓慢平滑移动获取一序列的 2D 超声数据图像，如图 7 所示。

针对基于距离加权的插值方法，通过实验发现：当半径较小时，如：R＝3，会产生空隙。经过实验分析，发现半径 R＝5 时，效果比较好，且没有了空隙。为了便于比较，后面实验设定插值半径大小值相同。对此采集的体模数据，分别用 SDW、HSDW(α＝2.0，α＝0.1)、ASDW(α＝1000，b＝2.0)算法进行重建。重建结果如图 8所示。

图 6 体模扫描实验环境Fig. 6. Snapshot for the phantom scanning

图 7 采集的 2D 超声图像序列Fig. 7. 2D ultrasound image slices

为了验证系统的可行性，对鸡肾进行了自由式三维超声扫描，相关的实验结果如图 9 所示。

图 8 实验体模及各种重建算法比较Fig. 8. Comparison for various reconstruction algorithms

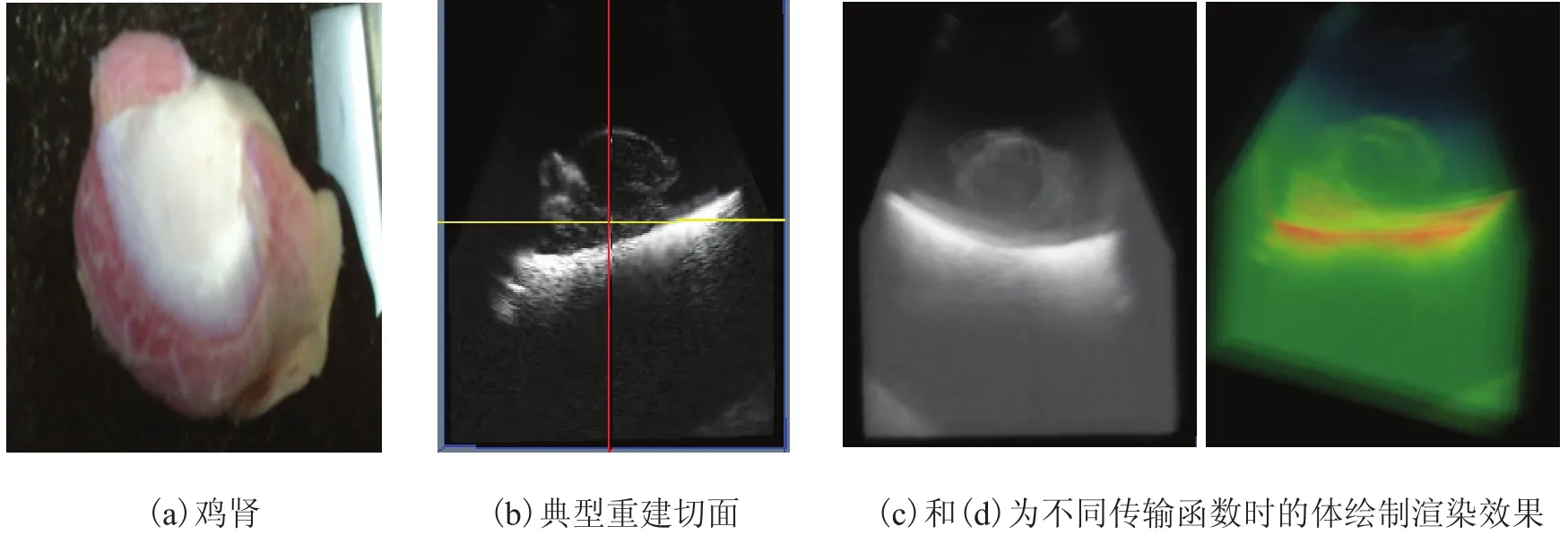
图 9 鸡肾的三维超声扫描Fig. 9. 3D ultrasound imaging for chicken kidney using the proposed systemDWD

4 实验分析

通过图 8 可以明显看出：(e)图重建的效果最好。与图(a)、(b)、(c)、(d)和(e)相比，图(b)较模糊，斑点噪声较多。对比图(d)和(e)，发现(d)图边缘和细节较(e)图模糊，(e)图比(d)斑点噪声大大降低。由此验证了在 HSDW 算法中，较小的 α 值能够较好地保持边缘，但仍然存在很多的斑点噪声；较大的 α 值虽然大大减少斑点噪声，但令边缘和细节变得模糊。图 8(e)很好的保持了这一平衡，使其能够在保持组织边缘的同时减少斑点噪声。

由于 ASDW 比 SDW 插值过程复杂，所以它的重建时间较 SDW 久，从程序运行的时间来看，ASDW 重建的时间差不多是 SDW 的 3 倍。通过对比，发现 DW 插值算法在斑点噪声和阴影减小方面表现得比较好。

表 1 重建时间比较Table 1. Comparison of the reconstruction time

5 结 论

本研究实现了一种基于光学定位的自由式三维超声成像系统，并在重建算法方面详细的介绍了几种基于距离加权的三维超声重建算法。通过在平方距离加权中引入自适应的调整参数 α，通过使每个体素的局部方差比和其球形邻域内的均值来控制权重分布。对于在其邻域内较高对比度的体素，参数 α 被分配为较小的值以保持图像边缘等特征；对于在其邻域内较低对比度的体素，参数 α 被设置成相对较大的值来减少均匀区域里的斑点噪声。在此基础上，ASDW 算法通过一个体素的领域统计，用指数函数来自动调节参数α。通过实验，结果成功的表明了这种方法的可行性。

在 ASDW 方法中，有两个积极的参数 α 和 b需要被实验者设置。参数 α 决定完整均匀区域的插值影响。参数 b 决定 σ2/μ 的影响。ASDW 能够很好的保持边缘细节和降低噪声，但是它的重建时间比较久。

通过重建效果图 8 和重建时间表 1，我们可以得出 ASDW 效果最好，但是速度最慢。为了保持重建时间和重建质量的平衡，我们选择HSDW 算法，通过控制 α 来保持边缘细节和降低噪声。

综上所述，我们的三维重建系统能很好的对体模和动物器官进行三维重建。接下来我们将重点研究重建的质量和速度，通过优化代码和提出新的重建算法来提高三维重建的效果。

[1] Solberg OV, Lindseth F, Torp HR, et al. Freehand 3D ultrasound reconstruction algorithm-a review [J]. Ultrasound in Medicine and Biology, 2007, 33(7): 991-1009.

[2] Rohling R, Gee A, Berman L. A comparison of freehand three-dimensional ultrasound reconstruction techniques [J]. Medical Image Analysis, 1999, 3(4): 339-359.

[3] Jose-Estepar RS, Martin-Fernandez M, Caballero-Martinez PP, et al. A theoretical framework to three dimensional ultrasound reconstruction from irregularly sampled data [J]. Ultrasound in Medicine and Biology, 2003, 29(2): 263-278.

[4] Penney GP, Joosten K, Letteboer MMJ, et al. Three dimensional reconstruction of tracked freehand ultrasound using non-rigid registration [J]. Biomedical Imaging, 2004, 1: 492-495.

[5] Coupe P, Hellier P, Azzabou N, et al. 3D freehand ultrasound reconstruction based on probe trajectory [C] // International Conference on Medical Image Computing and Computer-Assisted Intervention, 2005, 8(1): 597-604.

[6] Huang QH, Zheng YP. An adaptive squareddistance-weighted interpolation for volume reconstruction in 3D freehand ultrasound [J]. Ultrasonics, 2006, 44(Suppl 1): e73-e77.

[7] Fenster A, Downey DB. Three dimensional ultrasound imaging [J]. Annual Review of Biomedical Engineering, 2000, 2(1): 457-475.

[8] Dewi EO, Wilkinson MHF, Mengko TLR, et al. 3D ultrasound reconstruction of spinal images using an improved Olympic hole-filling method [C] // International Conference on Instrumentation, Communications, Information Technology, and Biomedical Engineering, 2009: 1-5.

[9] Sanches JM, Marques JS. A rayleigh reconstruction/interpolation algorithm for 3D ultrasound [J]. Pattern Recognition Letters, 2000, 21(10): 917-926.

[10] Welch JN, Johnson JA, Bax MR, et al. A real-time freehand 3D ultrasound system for image-guide surgery [C] // IEEE Ultrasonics Symposium, 2000, 2: 1601-1604.

[11] 耿俊卿. 三维超声成像系统体数据重建算法的应用研究 [D]. 济南: 山东大学, 2008.

[12] Luo X, Ding M, Zhou C. 3D ultrasound reconstruction based on rotational scanning coping with calibration uncertainty [C] // Proceedings of SPIE, Medical Imaging 2007: Visualization and Image-Guided Procedures, 2007.

[13] Gledhill D. Panoramic imaging-a review [J]. Computer and Graphics, 2003, 27(3): 435-445.

[14] Loupas T, McDicken W, Allan P. An adaptive weighted median filter for speckle suppression in medical ultrasonic images [J]. IEEE Transactions on Circuits and Systems. 1989, 36(1): 129-135.

Development of Freehand 3D Ultrasound Imaging System Based on
Optical Tracking Mechanism

WEN Tiexiang1,2QIN Wenjian1GU Jia1

1( Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055, China )
2( University of Chinese Academy of Science, Beijing 100049, China )

The freehand 3D ultrasound is a new imaging tool based on the ultrasonic imaging mechanism and spatial positioning apparatus. It can be used to image all kinds of samples and in-vivo human subjects freely by integrating the spatial positioning senor on the conventional 2D probe of the 2D ultrasound system. In this paper, a freehand 3D ultrasound with the application of minimally invasive surgery was developed. The popular distance-weighted interpolation method was well studied and applied in our imaging system. Experimental results on both phantom and chicken kidney demonstrate that the developed freehand 3D ultrasound system can produce satisfied images to prove the feasibility of the system.

ultrasound image; 3D reconstruction; distance-weighted interpolation; volume rendering

TP 391

A

2013-11-20

温铁祥，博士研究生，研究方向为医学图像处理和计算机视觉；秦文健，工程师，研究方向为模式识别和医学图像处理；辜嘉(通讯作者)，研究员，博士生导师，研究方向为计算机视觉和医学成像技术，E-mail：jia.gu@siat.ac.cn。