均值模型下满足对数级收敛速度的动态系统

宁 立

(中国科学院深圳先进技术研究院高性能计算技术研究中心 深圳 518055)

均值模型下满足对数级收敛速度的动态系统

宁 立

(中国科学院深圳先进技术研究院高性能计算技术研究中心 深圳 518055)

文章研究了在均值模型下，动态系统收敛至一致性状态所需的时间。在每一时间步内，节点计算其邻居的均值，并以计算结果作为自己的新值。我们考虑了当节点间的网络结构处于动态变化状态的情况。我们的分析证明了当节点的度在相邻时间点之间变化较小的情况下，即使仅满足微弱的连通性条件，动态变化的网络仍然可以保证动态系统会快速收敛到一致性状态。

对数级收敛； 一致性； 动态系统

1 Introduction

Many dynamic systems have been used to model the natural group behavior. Mathematically speaking, we consider the case when each individual or node in the set V maintains some real number, which can represent the opinion on some issue (e.g. preference in voting). In every time step, a node can collect the opinions of others and updates its opinion accordingly. Based on observations from many such systems[1-3], the values of all nodes converge to the consensus (a common opinion), after a small number of steps.

DeGroot[4]models the consensus of opinions using weighted averaging model. This model has been widely studied, where the interactions of the nodes in a step are modeled in a network Gt＝(V,Et). An edge {p, q} in Etindicates that node p and node q can collect each other’s number (opinion value) at time t. This weighed averaging model has applications in parallel computation[5], control theory[6-11]and ad-hoc networks[12].

Chan and Ning[13]studied what weighting strategies and what kind of networks can enable fast convergence to achieve consensus. They made a conjecture that in practical conditions, the averaging dynamic systems converged for the consensus logarithmically. In this paper, we consider a model which is essentially the same with the uniform averaging model[13], and the case when the underlying network topology is dynamic. Formally speaking, the networks Gts change over time. In general, we only assume the general structural properties of the networks, without specifying how they evolve.

In this paper, we prove that when degrees change mildly between two consecutive networks, the dynamic system converges logarithmically.

1.1 Related Work

Researchers have studied the special case of uniform averaging model with time-invariant topology[4].

If the underlying network is time-invariant and connected, Olshevsky and Tsitsiklis[14]showed that the convergence time for the uniform averaging model was O(n3), where n denoted the number of nodes.

Relatively, researchers know little about the convergence time in the cases of dynamic networks. Cao et al.[8]showed that the convergence time was nO(n)assuming some special structure in the networks. Olshevsky and Tsitsiklis[14]showed that the convergence time for the uniform averaging model was O(knkn), with the weak connectivity assumptions that the union of any k consecutive networks was connected. With the same weak connectivity assumption, Netic et al.[15]showed that the convergence time was O(kn2/α), for a class of averaging algorithms, where α is a lower bound of the non-zeros weights involved in the algorithms.

Chan and Ning considered the cases where the connectivity was characterized via the eigenvalue gap, and showed the polynomial convergence time with mild connectivity conditions[13]. In the same paper, they proved the logarithmic convergence for a special case named static weights model.

Vicsek et al.[16]studied the interaction between particles using the weighted averaging model. The particles influence each other when they are close enough, and the convergent state is achieved when all particles travel in the same direction. Jadbabaie et al.[6]gave an explanation theoretically to such convergent behavior. Chazelle[17]studied a discrete version and showed that the convergence time was the power tower of n.

Directed networks and asynchronous updates[7]were considered. Researchers have also studied the convergence under non-linear update rules[9-11].

1.2 Our Contribution

In this paper, we focus on the uniform averaging model, and the analysis between the convergence time and the topology of the evolving networks.

Following the idea proposed by Chan and Ning[13], we measured the connectivity of a network by the eigenvalue gap of its transition matrix. By an extension of Cheeger’s Inequality, it is shown that the constant eigenvalue gap implies the constant edge expansion of the network[13].

As the preparation for the main result, we firstly proved the logarithmical convergence for the specialcase which corresponds to the static weight model[13]. We harnessed an idea similar to the one used in the proof[13], and presented the proof under our model description.

For the uniform averaging model, we made an analysis of the conditions on the given network sequence such that the convergence was achieved fast. With the observation that the network in practice reflects the social situation of the individuals and evolves gradually, we are motivated to introduce the property of “mildly-changing” degrees, and finally, we proved that if the sequence of networks satisfied the property of “mildly-changing” degrees, and the network at any time point was well-connected (i.e. it had constant eigenvalue gap), then the dynamic system converged to the consensus in O(log n) time steps.

2 Preliminaries

2.1 Basic Notations

In this paper, we used ℝ to denote the set of real numbers. For a vector x with entries from ℝ, its i-th entry is referred to using x[i].

A simple undirected graph (or simply “network”) is usually denoted by G, and an edge between two nodes p, q in the graph is denoted by {p, q}.

2.2 Uniform Averaging Model

Since the model we will study is essentially the same with the uniform averaging model[13]introduced, we use the same model name.

Imagine we are given n individuals and each of them holds a quantity (velocity/opinion), which can be represented by a number from ℝ. A configuration at some time point is an n-dimensional vector fromℝnconsisting of each individual’s quantity. We denote the configuration at time t by vt.

At each time step, the individuals are supposed to form a network Gt, in which the nodes represent the individuals and the edges reflect the association between two nodes. It is obvious that all Gts have the same number of nodes.

Definition 1(Dynamic System: Uniform Averaging Model) Briefly speaking, a dynamic system indicates how to update the quantities associated with each member of a given group of individuals, according to some relation among these individuals.

In this paper, we consider the dynamic systems, in which the relations between individuals are reflected by the network Gt, and the updating process is represented by a product of a row stochastic matrix Ptand the vector consisting of the individuals’quantities, where Pt, is the transition matrix of Gt, is defined as,

In the equation, Inis the n×n identity matrix and Ltis the Laplacian of Gt:

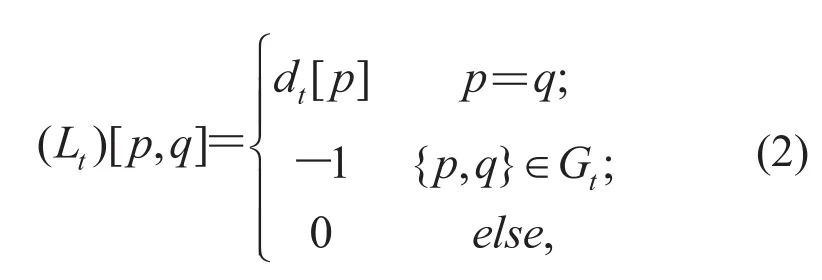
and Ctis a diagonal matrix, in which the i-th diagonal entry is denoted by ct[p], and satisfies

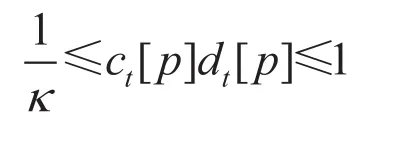
where κ1 is a constant and the notation dt[p] denotes the degree of node p in Gt.

When a dynamic system is given, it actually means that the strategy to calculate Ctfrom a given network Gtis valid. Then the process updating configuration vtto vt+1is defined as

Denote a sequence of networks as

Generally we have s＝0 and f＝∞, thus we use to simply denote

In the remaining argument, we always suppose the dynamic system was already given (including the networks , Cts and constant κ that defines the updating rules of vt). Then with an initial configuration v0and a given sequence of network G, we want to consider when the corresponding updating process converges and try to derive an upper bound of the converging rate.

2.3 Matrix notations

As there are a lot of matrix operations involved in our argument, we introduced some notations of matrix operations in this section.

For any matrix M from ℝn×n, the trace is defined as the sum of the diagonal entries, i.e.

where M[i, i] denotes the i-th diagonal entry of the matrix M.

Next we introduced the τ1and τ2measures which reflect the variance between row vectors in a matrix. The τ1-measure of M, is defined as

and the τ2-measure of M is defined as

In particular, when M is of dimension n×1, i.e., M is a vector, another measure τ which doubles τ1is also used a lot. That is:

Note that in such case (M is a vector), it holds that

There are some useful facts about the τ1and τ2measures. Fact 1 states an important relationship between the τ2-measure of the product of two matrices and product of the measures of the corresponding matrices, which is proved by Chazelle and Moreau[17,18], fact 2 relates the τ1-measure of a stochastic matrix with its smallest entry. Its proof is too trivial to be mentioned here.

The notation of stochastic matrix is needed for the introduction of facts. A matrix M is called stochastic if the entries sum up to 1, for every row vector in M.

Fact 1For any stochastic matrix A and any matrix B, whose dimensions are compatible with A such that AB is well-defined, we have

Based on fact 1, any stochastic matrix P has the property that τ1(P)1. Hence, it follows that for all ts,

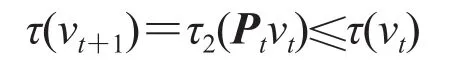
Fact 2Suppose P is a stochastic matrix so that in all its entries, there are at least some number α＞0. Then, it holds that

3 Convergence for Consensus

3.1 Simple Case: When CtRemains the Same

In this section, at first we consider a case which is similar to the static weight model introduced by Chan and Ning[13]. Specifically, we assume Ctremains the same while the underlying network Gtchanges.

Theorem 1Provide an initial configuration v0and a sequence of networks , if all Cts used for computing Pts are the same, denoted by C, and the second largest (magnitude) eigenvalue of any Ptis bounded by a positive number λ＜1, then for any ε＞0, there is

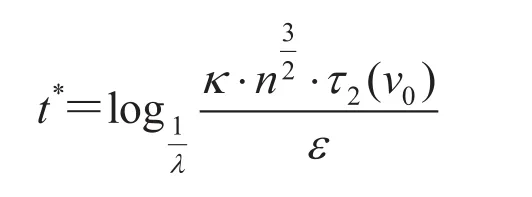
such that

as long as t＞t*, where cmaxdenotes the largest element of C1/2and κ appears in the constraints for Ct’s, i.e., for any p and t, it always holds that

ProofFirstly, recall the facts that Ptis in the form of In—CLt, and ct[p]＞0 for all p. Being a stochastic matrix, Pthas the dominant eigenvalue 1 with right eigenvector 1 and left eigenvector

Define a matrix Mtas

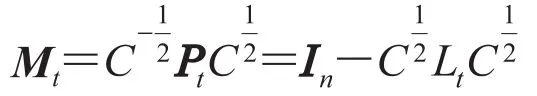
Then Mtis symmetric and consequently can be diagonalized as whereare orthonormal eigenvectors and the eigenvalues are real.

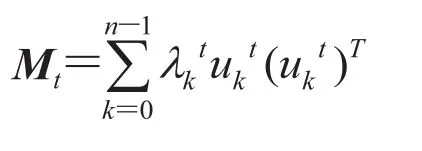
Remark 1Here the superscript t over the eigenvalue λ refers to the time point associated with the matrix Mt. To avoid confusing (with the “power”), we ignore this label t (or sometimes i) when it is clear from the context.

By the connectivity of Gt, stochasticity of Pt, and other properties according to the spectral graph theory, we have

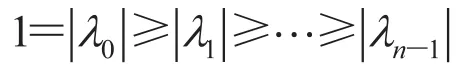
and

for every t. Because all s are the same, we simply write u0to avoid distinguishment.

Use e(i) to denote the n-dimensional vector in which the i-th coordinate is 1 while the others are all zeros. Then the production of the transition matrices from time 0 to time t—1 is

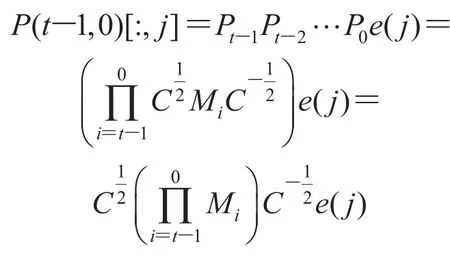
Focus on the product of Mis,

Each Mican be rewritten as

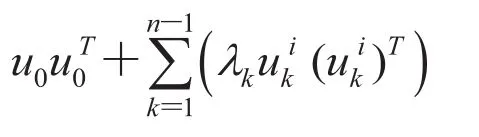
Because uk(i)s are orthonormal unit vectors, they form actually an orthonormal basis. Thus,

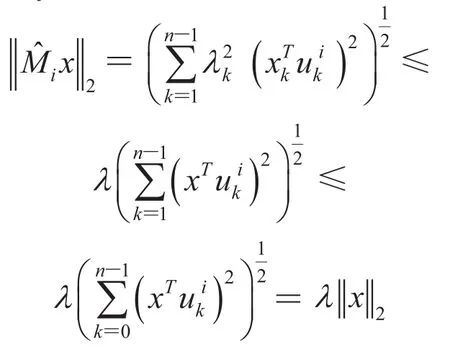
Then, we rewrite P (t—1, 0)[:, j] as

The last equality holds because u0is orthogonal to any uk(i) (k＞0), which impliesRecall that u0is an unit vector. Thus, we have

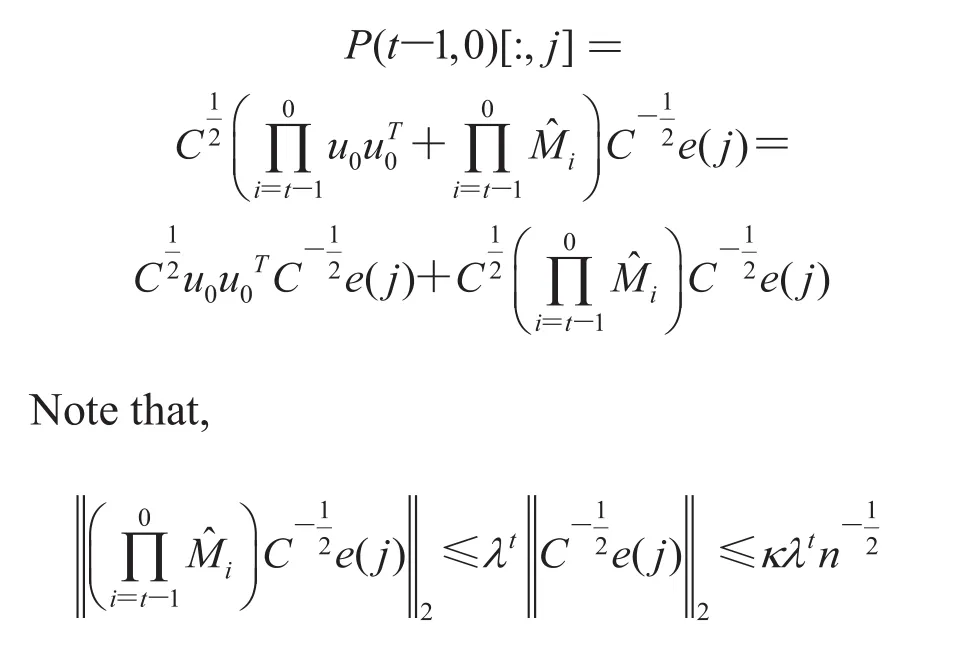
and any entry of C is upper bounded by 1. Then we get

3.2 General Case: When CtChanges

Chan and Ning[13]made a conjecture that in practical conditions, the averaging dynamic systems converged for the consensus logarithmically. In this section, we introduced a condition which was mild and appeared normally in practice, and then proved that under such a condition, the conjecture made by Chan and Ning[13]is true.

Condition 1(mildly changing degree) Provide a sequence of networks , if μ＞0, then for any time t and node p, it holds that

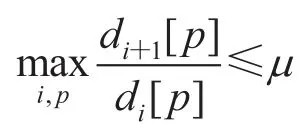
then we say that the given network sequence has“mildly-changing” degrees.

Theorem 2Provide an initial configuration v0and a sequence of networks which has“mildly-changing” degrees, and the second largest (magnitude) eigenvalue of Ptis bounded by a positive number λ＜1 for every t＞0, then the dynamic system converges for the consensus at a rate of order O(log n).

ProofAt first, recall that

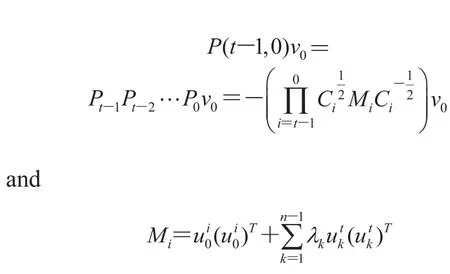
To simplify the presentation, use the notation

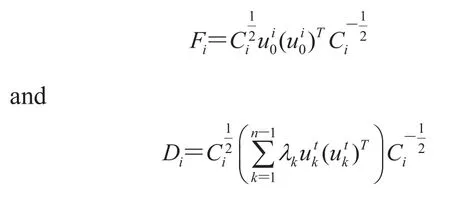
Note that for any i,

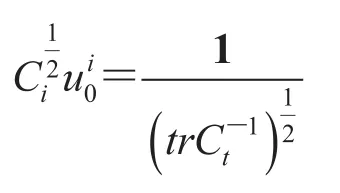
Note that the first part

is a vector along the direction 1, thus it decides the consensus which is finally achieved, if the remaining partconverges to 0. Note that

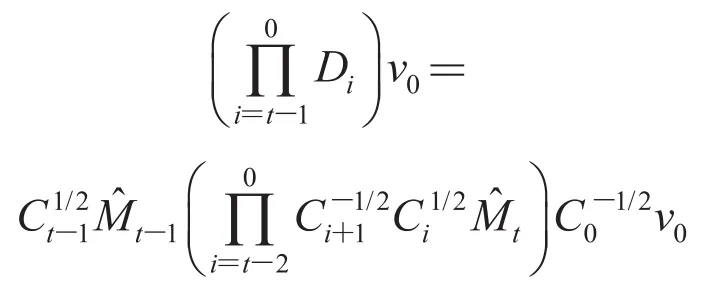
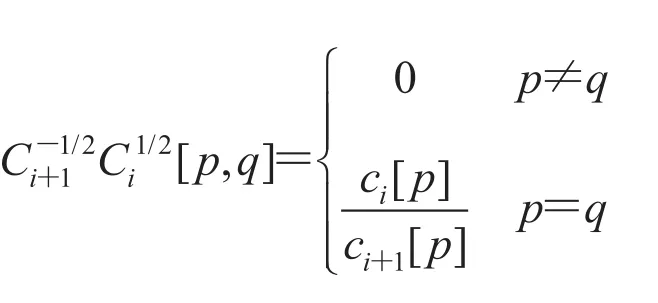
and recall that

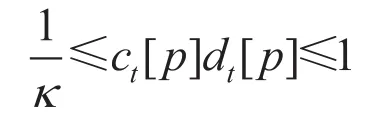
Thus we have

Recall the “mildly-changing” property of the degrees, i.e. there exists μ＞0, then

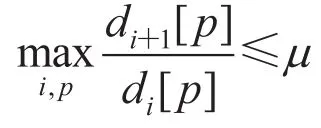
Hence we finally get

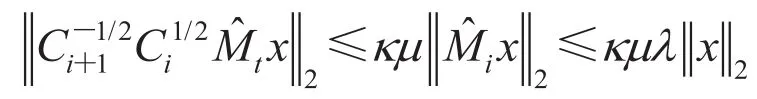
which implies that

for any ε＞0, and t＞t*, where t*＝O(log n). The detailed analysis of t*is ignored since it is similar to the proof of theorem 1.

4 Conclusions

In this paper, we confirmed the conjecture raised by Chan and Ning[13]that concluded the logarithmic convergence for consensus of dynamic systems, under the “mildly-changing” degree condition. As in practice, the degree of a node reflects the personal social situation, which usually evolves gradually, the property of “mild-changing” degree is easily satisfied. Hence, our results help people to understand the fast convergence of group behavior in natural world, like bird flocking.

[1] Reynolds CW. Flocks, herds, and schools: a distributed behavioral model [C] // Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, 1987: 25-34.

[2] Tanner HG, Jadbabaie A, Pappas GJ. Flocking in fixed and switching networks [J]. IEEE Transactions on Automatic Control, 2007, 52(5): 863-868.

[3] Cucker F, Smale S. Emergent behavior in blocks [J]. IEEE Transactions on Automatic Control, 2007, 52(5): 852-862.

[4] DeGroot MH. Reaching a consensus [J]. Journal of American Statistical Association, 1974, 69(345): 118-121.

[5] Bertsekas DP, Tsitsiklis JN. Parallel and Distributed Computation: Numerical Methods [M]. USA: Prentice Hall, 1989.

[6] Jadbabaie A, Lin J, Morse AS. Coordination of groups of mobile autonomous agents using nearest neighbor rules [J]. IEEE Transactions on Automatic Control, 2003, 48(6): 988-1001.

[7] Cao M, Morse AS, Anderson BDO. Coordination of an asynchronous, multi-agent system via averaging [C] // Proceedings of the 16th International Federation of Automatic Control World Congress, 2005: 1080, doi: 10.3182/20050703-6-CZ-1902.01081.

[8] Cao M, Spielman D, Morse AS. A lower bound on convergence of a distributed network consensus algorithm [C] // Proceedings of the 44th IEEE Conference on Decision and Control, 2005 and 2005 European Control Conference, 2005: 2356-2361.

[9] Fang L, Antsaklis PJ. On communication requirements for multi-agent consensus seeking [C] // Proceedings of the Workshop on Networked Embedded Sensing and Control, 2005: 53-67.

[10] Cortés J. Finite-time convergent gradient flows with applications to network consensus [J]. Automatica, 2006, 42(11): 1993-2000.

[11] Lorenz DA, Lorenz J. Convergence to consensus by general averaging [C] // Proceedings of the 3rd Multidisciplinary International Symposium on Positive Systems: Theory and Applications, 2009: 91-99.

[12] Liu YB, Yang YR. Reputation propagation and agreement in mobile ad hoc networks [C] // Proceedings of Wireless Communications and Networking Conference, 2003: 1510-1015.

[13] Chan TH, Ning L. Fast convergence for consensus in dynamic networks [C] // Proceedings of the 38th International Colloquium of Automata, Languages and Programming, 2011: 514-525.

[14] Olshevsky A, Tsitsiklis JN. Convergence speed in distributed consensus and averaging [J]. SIAM Journal on Control and Optimization, 2009, 48(1): 33-55.

[15] Nedic A, Olshevsky A, Ozdaglar A, et al. On distributed averaging algorithms and quantization effects [J]. IEEE Transactions on Automatic Control, 2009, 54(11): 2506-2517.

[16] Vicsek T, Czirok A, Ben-Jacob E, et al. Novel type of phase transition in a system of self-driven particles [J]. Physical Review Letters, 1995, 75(6): 1226-1229.

[17] Chazelle B. Natural algorithm [C] // Proceedings of 20th Annual ACM-SIAM Symposium on Discrete Algorithms, 2009: 422-431.

[18] Moreau L. Stability of multi-agent systems with time-dependent communication links [J]. IEEE Transactions on Automatic Control, 2005, 50(2): 169-182.

Logarithmic Convergence for Consensus of Dynamic Systems

NING Li
( Center for High Performance Computing, Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055, China )

In this paper, the convergence time required to achieve consensus of dynamic systems was studied under the uniform averaging model. In each time step, a node’s value was updated to some weighted average of its neighbors’ and its old values. The case was studied when the underlying network was dynamic. Our analysis results show that dynamic networks exhibit fast convergence behavior as long as the nodes’ degrees change gradually, even under very mild connectivity assumptions.

logarithmic convergence; consensus; dynamic system

TP 393 TP 301

A

2013-12-23

宁立，博士，研究方向为分布式算法和推荐系统，E-mail：li.ning@siat.ac.cn。