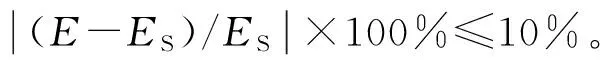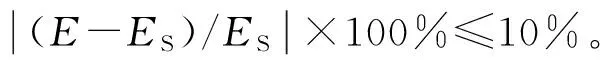硬涂层-薄板的阻尼特性、非线性振动与减振优化设计*
陈玉刚 翟敬宇 杨铮鑫 韩清凯
硬涂层-薄板的阻尼特性、非线性振动与减振优化设计*
陈玉刚 翟敬宇 杨铮鑫 韩清凯(通信作者)
陈玉刚 博士研究生 116024 辽宁省 大连市 大连理工大学 机械工程学院 chenyg@mail.dlut.edu.cn
翟敬宇 工学博士 讲师 116024 辽宁省 大连市 大连理工大学 机械工程学院 zhaijy@dlut.edu.cn
杨铮鑫 工学博士 讲师 110142 辽宁省 沈阳市 沈阳化工大学 能源与动力工程学院 zhengxin1021@sina.com
韩清凯 工学博士 教授 116024 辽宁省 大连市 大连理工大学 机械工程学院 hanqingkai@dlut.edu.cn
在中国国家重点基础发展计划(973计划)项目《高端压缩机组高效可靠及智能化基础研究》和《硬岩掘进装备的关键技术问题》,中国国家自然科学基金资助项目《薄壁构件硬涂层阻尼减振的多尺度模拟方法与主动设计》和《弹性支承多转子系统的不对中建模与振动分析》,中央高校基本科研业务费专项资金资助项目《硬涂层薄板复合结构的减振机理及振动疲劳特性研究》的共同资助下,针对硬涂层-薄板的阻尼特性、非线性振动与减振优化设计等问题,通过理论推导、模型建构、数值仿真,以及实验测试等方法,建立起由硬涂层材料力学特性参量的辨识以及硬涂层-薄板动力学建模、非线性振动、减振阻尼优化设计等组成的硬涂层-薄板阻尼特性、非线性振动与减振优化设计理论体系,报告学术研究成果。
采用电子束物理气相沉积(EB-PVD)在不锈钢梁上制备了NiCrAlY硬涂层。采用纳米压痕实验,结合压痕过程的有限元模拟,在各向同性弹性材料和各向异性弹性材料等2种本构关系简化假设下,辨识硬涂层力学特性参数(主要是弹性模量)。当硬涂层简化为各向同性弹性材料时,以压痕实验加载曲线为依据,通过无量纲分析和有限元模拟,求解出虑及基体效应的NiCrAlY硬涂层材料的弹性模量(E=168.44 GPa)。当硬涂层简化为各向异性弹性材料时,通过简化硬涂层本构模型,确定需要求解的独立横观各向同性材料力学特性参数是ET(横向弹性模量)和EL(纵向弹性模量);采用量纲分析和有限元模拟,得到了压痕实验响应过程中的最大加载力、加载曲线指数与硬涂层材料力学特性参数之间的无量纲方程,求解出ET=133.17 GPa和EL=181.21 GPa。
以涂敷NiCrAlY硬涂层的悬臂钛合金薄板为对象,将辨识得到的各向同性材料参数和各向异性材料参数分别代入,建立涂层-薄板复合结构(CP-Structure)有限元模型,对CP-Structure的固有特性和振动响应进行数值分析。通过对比采用辨识方法得到的各向同性材料参数,以及由横观各向同性材料参数计算得到的固有频率与实验测试结果的差异率,发现采用横观各向同性材料参数的固有频率计算结果在高阶部分(4~8阶)与实验测试得到的结果更为接近(差异均在2%以内)。这说明,硬涂层结构高阶振动特性分析,以及硬涂层对高周疲劳抑制研究,应当采用横观各向同性本构关系。
针对薄板高阶共振引起的疲劳破坏,基于薄板结构的减振指标(包括固有频率、阻尼比、振动幅值、振动应力、疲劳寿命等),选取悬臂钛板的典型模态,采用数值计算与实验测试对照分析等方法,综合评价硬涂层-薄板的减振效果。结果表明:涂敷NiCrAlY硬涂层后,悬臂钛合金板的前10阶固有频率都出现了上升(上升幅度为1.600%~1.972%);前10阶模态阻尼比大部分有所上升(15.79%~160%),但有例外(第3阶略有降低、第5阶基本不变);容易引起悬臂钛板疲劳破坏的第4阶及第10阶模态,共振状态下振动幅值及振动应力明显下降。
将硬涂层-薄板整体等效为特定非线性材料制成的薄板,基于非线性弹性板动力学理论,采用Galerkin法和小参数法,解析了虑及材料非线性的硬涂层-薄板的固有特性。虑及复合材料悬臂板几何关系线性、材料非线性弹性,建立了硬涂层-薄板非线性运动方程(NKEHCTP);采用Galerkin法将NKEHCTP转化为非线性常微分方程,采用小参数法将其展开成一系列线性微分方程进行求解,获得了悬臂硬涂层-薄板非线性振动特性的近似解析解;采用有限元法和实验测试法对近似解析解进行了比较和验证。通过对3个不同尺寸、不同涂层材料的悬臂硬涂层-薄板固有频率的计算,发现非线性解析方法和有限元方法求得的固有频率与实验测试的结果均贴近(最大差异9.47%),线性解析方法求得的固有频率在3阶以后相差比较大(最大差异17.59%)。证明采用非线性弹性板理论分析CP-Structure的高阶振动特性,可以得到比较精确的计算解。
基于von Karman理论和Reddy三阶剪切变形理论,采用Hamilton变分原理建立起硬涂层-薄板非线性动力学方程(NDEHCTP)。利用Galerkin法离散NDEHCTP,得到了硬涂层-薄板横向变形非线性振动方程。分别以悬臂薄板和悬臂硬涂层-薄板为研究对象,对其在横向谐波激励作用下的响应进行实验考察,得到了激振频率的变化对两类结构振动响应的影响。结果表明,悬臂硬涂层-薄板比悬臂薄板的振动行为更加复杂,但是发生混沌运动的区间要比悬臂薄板小;尤其是在高频率范围,硬涂层抑制了混沌运动的发生。
以提高复合结构强度和显著提高结构系统阻尼特性为目标,建立了以组合性能指标Etanδ最大化为核心的涂层阻尼减振优化设计体系,创立了硬涂层-薄板结构阻尼减振优化设计方法;建立了基于Reuss模型的复合结构力学特性计算模型(MMCSBRM),给出了硬涂层阻尼减振的优化设计流程(ODPBRM);以钛合金薄板为例,采用ODPBRM对硬涂层材料的弹性模量、损耗因子和涂敷厚度等参量进行寻优,讨论了它们对于CP-Structure整体动力学特性的贡献。采用有限元法,对硬涂层处理前后的薄板整体的固有特性、模态阻尼比和谐响应等减振指标进行阻尼减振效果对比验证。结果表明,在3 mm钛板上涂敷硬涂层后,其最优设计工况下,发生了频率偏移(增大2.49%~2.70%)、模态阻尼比显著增加(增加13.62%~16.82%)、谐响应共振峰显著降低(降低90%以上)等现象,证实减振优化设计具有明显效果。
通过研究,针对硬涂层-薄板的阻尼特性、非线性振动与阻尼优化设计建立起较为系统的分析架构,建立了硬涂层材料力学参数辨识的方法、CP-Structure的有限元模型及非线性动力学方程、硬涂层减振有效性的评估以及硬涂层阻尼减振的优化设计流程,得到了12项科学结论,提出了硬涂层在科学研究与工程应用中需要进一步研究的问题。
硬涂层-薄板 非线性振动 阻尼减振 阻尼减振优化设计 硬涂层材料力学参数辨识 各向同性弹性材料 各向异性弹性材料 减振有效性 非线性弹性复合层板 涂层-薄板复合结构有限元模型 硬涂层-薄板非线性动力学方程 基于Reuss模型的复合结构力学特性计算模型
1 引言
涂层技术(Coating Technology)是针对结构表面进行材料涂覆,以实现结构性能大幅提升的技术形式[1]。目前,涂层技术正在成为改善工程结构性能重要且有效的技术,甚至正在成为一项关键的技术,在航空、航天、制造等领域开始得到应用[2]。
薄板结构(Thin-Plate Structure)在工程中大量使用。在工程实践中,可以采用涂层技术提高薄板结构的强度或刚度,特别是改善其动力学性能。
在薄板结构的现有涂层中,金属基涂层(Metallic Coating)或陶瓷基涂层(Ceramic Coating) 被称为硬涂层(Hard Coating),以区别于有机高分子基软涂层(Organic Polymer Soft Coating)。由于硬涂层具有耐高温、耐摩擦、性能稳定等优势,可以应用硬涂层技术来改善机械结构件的表面强度,以及改善抗冲刷、抗磨损、抗腐蚀等性能。
应用硬涂层,一方面着力于提高传统材料的工程应用能力,另一方面着眼于创造新的复合功能结构。最近十余年来,面向航空航天结构件的热障保护,抗高温热障涂层正在得到广泛研究与应用[3]。
近期的研究表明,在关键结构件上涂覆硬涂层可以增加结构的阻尼能力。Blackwell[4]通过实验评价了镁铝晶体(MgO+Al2O3)的阻尼减振能力,证实较之未涂敷镁铝晶体涂层,涂敷了镁铝晶体的钛板,其阻尼系数显著提高。Movchan[5]等学者在钛合金叶片上涂敷Sn-Cr-MgO涂层后,叶片复合结构的耗散能量明显增大。上述工作引导了近年来国际上研发阻尼硬涂层(Damping Hard Coating),特别是研究硬涂层阻尼特性(Damping Characteristic of Hard Coating )的努力。
由于高周疲劳(High-Cycle Fatigue)导致航空发动机压气机叶片等典型薄壁结构件故障率居高不下,故而利用阻尼涂层提高薄壁构件的振动疲劳寿命具有重要意义。同时,考虑涂层的抗冲刷性能与阻尼性能的双功能或多功能涂层技术的研究,引起学界和工程界的高度重视[6]。
本研究团队开发的用于航空发动机薄壁构件的阻尼硬涂层,在具备抗冲刷能力的同时,更能够产生突出的阻尼减振作用,可以抑制高周疲劳失效(High-Cycle Fatigue Failure)。
1.1 硬涂层材料的特性
1.1.1 常见的硬涂层材料
目前,阻尼硬涂层材料主要有金属基涂层材料、陶瓷基涂层材料,以及上述两者混合制作的涂层材料。
金属类涂层有铁磁合金(XCrAlY)涂层,陶瓷类涂层有MgAl2O4涂层或YSZ涂层(钇稳定氧化锆,Yttria-Stabilized Zirconia)。
复合涂层一般是以NiCrAlY为过渡层,再在过渡层上面制备金属涂层或陶瓷涂层。硬涂层阻尼材料有MgO+Al2O3[1],Sn-Cr-MgO[2],TiN[7],NiCoCrAlY[8],等等。NiCrAlY涂层由于具有很好的抗高温氧化、抗热腐蚀能力,良好的塑性和热疲劳性能,以及与陶瓷、合金良好的结合性能而得到广泛应用[9]。在热障涂层中,NiCrAlY一般作为过渡涂层使用,其组分中,Al有助于促进形成氧化膜,提高涂层高温氧化性能;Cr有助于改善抗热腐蚀性能;Y不仅能促进Al氧化膜的形成,还能提高涂层表面氧化膜的黏附性,改善氧化膜力学性能。
1.1.2 制备工艺及其微观结构特点
除了确保硬涂层具有良好的阻尼特性,表面光洁度(Surface Finish)、与基体的界面结合强度(Interfacial Strength)、抗疲劳性能(Anti-fatigue Performance),以及热稳定性(Thermostability),都需要考虑。
常见的涂层制备技术(Coating Deposition Technology)包括电镀(Electroplating)、化学镀(Chemical Plating)、热喷涂(Thermal Spraying)、热浸镀(Hot Dipping)、物理气相沉积(Physical Vapor Deposition,PVD)、化学气相沉积(Chemical Vapor Deposition,CVD)、分子束外延(Molecular Beam Epitaxy,MBE)、离子束合成(Ion Beam Synthesis)。合金类涂层制备,PVD和等离子喷涂(Plasma Spraying,PS)目前较为常用[10-11]。
PVD是将原子或分子从气相中沉积到基体表面,主要以磁控溅射(Magnetron Sputtering)和电弧离子镀(Arc Ion Plating)为主。相对于PS制备的涂层,PVD涂层致密,质量较高,表面光洁度、抗氧化和热腐蚀等性能更好;对于涂层晶体结构、厚度等参数的控制相对精确,而且需要控制的涂层制备参量较少。目前,工作在恶劣环境下的热端部件(如航空发动机叶片),其热障涂层均采用电子束物理气相沉积(Electron Beam Physical Vapor Deposition,EB-PVD)。
PS效率较高,适合异形工件表面涂层,但涂层的表面粗糙度(Surface Roughness)和涂层结构的控制不如PVD。PS涂层的形貌结构与PVD涂层存在很大差别(见图1),PS涂层以层状结构为主,而PVD涂层则多是柱状晶结构(注:示意图来自文献[10])。

图1 PS和PVD得到的涂层典型微观结构Fig.1 Microstructure of coating prepared by PS and PVD
1.1.3 力学特性及其阻尼机制
硬涂层通常具有各向异性和非线性等特点,且受涂敷工艺影响明显。尺度效应、界面、微观结构等参数决定着涂层的力学性能。
(1)各向异性 由于涂层制备过程形成的特殊微观结构(如柱状或层状),以及存在大量孔洞、微裂纹等因素,导致硬涂层材料的力学特性表现出各向异性[10]。例如,采用PS制备的涂层,通常其垂直方向的弹性模量要小于平面方向的弹性模量[12]。
EB-PVD制备的热障涂层横截面[13],涂层厚度方向上的弹性模量与平面内的弹性模量明显不同,并且在靠近界面处与涂层表面处的模量值相差很大(见图2)。

图2 不同深度处涂层不同方向上的弹性模量[13]Fig.2 Elastic modulus of different directions near interface and surface[13]
(2)非线性 在实际结构系统中,硬涂层经常表现出应变依赖性(Strain Dependence)——力学特性参数[主要有弹性模量(Elastic Modulus)及损耗因子(Loss Factor)]随应变幅度的变化而变化[14];涂层复合结构通常表现出软式非线性(Softening Nonlinearity)——其刚度随着激励力幅的增大而减小,固有频率也随之降低[15]。Torvik[16]测试了涂敷MgO+Al2O3涂层的梁,扫频曲线表明,随着扫频能量增高,曲线峰值点向左侧发生明显偏移,当能量足够大时,出现了非线性跳跃现象。
(3)阻尼特性 硬涂层阻尼减振的机理源于涂层颗粒之间的内部摩擦[17]。与粘弹性阻尼材料(Viscoelastic Damping Material)相比,硬涂层的性能更稳定,且耐高温、耐腐蚀,等等[18]。Patsias[19]和Ivancic[20]等学者发现,硬涂层在很宽的频率范围和温度范围内降低了发动机叶片的振动响应,增加了叶片的疲劳寿命。
(4)力学特性和阻尼特性受涂敷工艺影响 从化学成分分析,硬涂层材料主要是合金材料和陶瓷材料的混合体,其力学特性与单一材料和块状材料有很大不同,主要表现为受涂层制备过程的影响较大。以PS为例,涂层弹性模量受给料颗粒的尺寸、物相组成、喷涂过程和后处理等因素的影响[21]。因此,即使同一材料的涂层,制备工艺参数不同,也会导致形成不同的力学特性。
1.2 硬涂层复合结构的振动特性及减振有效性分析
硬涂层-薄板振动特性分析,必须考虑硬涂层材料的各向异性,以及复合层材料的典型特征,特别是本构关系的材料非线性特征。因此,将硬涂层-薄板整体等效为具有材料非线性的板,基于等效非线性弹性板理论,研究其固有特性十分必要。
早期,悬臂板(Cantilever Plate)研究集中于求解方法。Leissa[22]等学者使用的Rayleigh-Ritz是一种有效的求解方法。为了获得更为精确的结果,许多学者将寻找一组合适的形函数(Shape Function)作为研究重点,根据梁的函数建立起悬臂板形函数。Gorman[23]使用叠加的傅里叶级数来处理各向同性悬臂板(Isotropic Cantilever Plate),并将其工作推广到各向异性材料等情况[24]。
硬涂层材料参数与空间坐标有关,其控制方程是变系数的,在数学上很难取得直接解析解。目前,对功能梯度材料(Functionally Graded Materials,FGM)常见的板壳结构(Plate and Shell Structure)力学分析,主要采用层合模型法(Laminated Model Method)[25]、渐进解法(Asymptotic Solution)[26]、三维分析法(Three Dimensional Analysis)[27],以及简化模型法(Simplified Model Method)[28],等等。由于数学分析获得的是数值解,能够取得完全解析解,主要还是特定几何形状与边界条件的线性问题。
对于硬涂层材料的减振有效性分析与评价,Blackwell[4]等学者从实验角度评价了采取PS在钛板(Ti-6Al-4V)上喷涂MgO+Al2O3涂层后对于板振动的抑制效果;测试结果表明,涂敷阻尼材料后,整个结构系统出现了固有频率偏移、振幅下降、涂层板的阻尼特性显著提高等现象。
Patsias[19]和Tassini[12]等学者,采用APS和EB-PVD在Fe-Cr-Ni合金梁上沉积ZrO2-Y2O3陶瓷涂层,研究了阻尼及刚度特性。结果表明,采用APS沉积的陶瓷涂层比采用EB-PVD沉积的陶瓷涂层具有更高的阻尼能力,但弹性刚度更低,振幅依赖性更强。
徐惠彬[18]等学者在不锈钢梁上制备了NiCrAlY,FeCrMo,ZrO2等涂层,采用动态力学热分析(Dynamic Mechanical Thermal Analysis,DMTA)和弯曲共振法(Bending Resonance Method,BRM)进行测试,发现涂层后质量因子(Quality Factor)的倒数(Q-1)明显增大,涂层梁的固有频率上升,共振峰值明显降低。
Yen[29]等学者以梁和真实叶片结构为对象,应用铁磁性涂层增强涡轮叶片的阻尼能力;通过创建涂层结构系统的解析模型及有限元模型,分析铁磁涂层对叶片弦向弯曲模态的振动抑制效果;结果显示,铁磁性涂层对条纹模态(Stripe Mode)的振动具有明显抑制作用并显著减小了交变应力。
1.3 硬涂层-薄板的非线性振动
工程系统中存在广泛的非线性因素,例如,作用力非线性(Mechanical Nonlinearity)(如电场力、磁场力、万有引力等)、运动学非线性(Kinematic Nonlinearity)(法向加速度、科氏加速度等)、材料非线性(Material Nonlinearity)(非线性本构关系等)、几何非线性(Geometric Nonlinearity)(弹性大变形等),等等。因此,工程中的实际振动系统大多为非线性系统(Nonlinear System)。
由于可求出精确解的非线性系统极少,对于大多数非线性系统来讲,只能采用近似解析方法。
解析方法包括定性分析法(Qualitative Analysis Method)和定量分析法(Quantitative Analysis Method)。根据微分方程本身的结构而不是解的表达式研究解的局部或全局形态,即直接研究由微分方程所确定的积分曲线的几何性质,属于微分方程的定性分析范畴;定量分析法是寻找微分方程的近似解。建立悬臂边界下硬涂层-薄板的非线性动力系统数学模型(Mathematical Model for Nonlinear Dynamic System of Cantilevered CP-Structure)是定量分析的基础。
Reddy[30-32]提出了三阶剪切变形层合板理论(Three-order Shear Deformation Theory of Laminated Plates)来简化位移场,并在此基础上提出了考虑压电效应的板壳理论方法(Plate and Shell Theory with the Piezoelectric Effect )。Shih[33]给出了任意弹性基础上简支和固支层合薄板的非线性振动分析及其响应。Han[34]等学者分析了同性固支矩形板的几何非线性自由振动,讨论了平面内膜力对几何非线性行为的平均影响。
Turkmen[35-37]等学者研究了受稳态冲击波作用的层合板动力学响应行为,并且对比讨论了解析分析、有限元数值计算与实验测试不同方法得到结果的异同。Zhang[38]和郝五零[39]等学者研究了参数激励下薄板的全局非线性动力学问题。Zhang[40-47]所在的研究团队把全局分叉(Global Bifurcations)和混沌动力学(Chaotic Dynamics)、规范形(Normal Form)的理论和应用、全局摄动法(Global Perturbation Method)、全局动力学(Global Dynamics)等现代非线性动力学理论(Modern Nonlinear Dynamics Theory)应用于梁的非线性振动分析,得到了一系列理论解析、数值与实验结果。
对于硬涂层薄板非线性振动,大部分研究集中于稳定性分析(Stability Analysis)、分叉(Bifurcations)、混沌(Chaos)等非线性动力学特性,实验研究相当欠缺。硬涂层薄板非线性振动的实验研究,对于掌握硬涂层薄板的固有特性和非线性振动行为有着十分重要的现实意义。
矩形板(Rectangular Plate)是最常见工程结构之一。迄今为止,许多国外学者以矩形板为对象(包括金属板和复合层板)进行了实验研究,发现了一系列非线性现象,并对板的非线性振动问题进行了综述[48-53]。
Yamaki[54-55]等学者针对夹持矩形板(Clamped Rectangular Plate)在均匀分布周期载荷(Uniform-distributed Tangential Load)下的非线性响应进行了实验分析,发现对于稳态对称周期响应(Steady Response of Symmetry Cycle),大部分实验值与理论值能够很好地吻合;而非对称、非周期响应(Asymmetric, aperiodic response)与内共振(Internal Resonance)、混合共振(Hybrid Resonance)、动力突跳现象(Dynamic Mutation Phenomenon)有一定关系。
Oh[56-57]等学者利用实验方法,研究了简谐激励(Harmonic Excitation)作用下的复合材料层合板非线性振动(Nonlinear Vibration of Composited Plate),利用实验分析了石墨纤维树脂悬臂板(Graphite-Epoxy Cantilever Plate)的复杂动力学行为。实验观测到了与弹性梁相似的从高频到低频模态的能量转换,还观测到对于一些激励在高频-低频模态相互作用时,同时伴随着2∶1的内共振。
Amabili[58]等学者研究了不锈钢矩形薄板在受到不同集中质量时的高振幅受迫振动;实验的边界条件与四边固支的矩形板接近,竖直或水平放置薄板,以研究重力的影响;实验发现,由于重力使水平薄板产生弯曲挠度,使得集中质量能够减小水平薄板的硬式非线性特征(“Hardening” Nonlinear Characteristics),而对竖直薄板的非线性振动趋势没有影响。
1.4 硬涂层减振优化设计
硬涂层薄板的阻尼优化设计,目前鲜有报道。对于薄板实施硬涂层阻尼减振优化设计,可以借鉴针对粘弹性自由层和约束层阻尼的优化设计方法。例如,Kim[59]等学者采用Golla-Hughes-McTavish(GHM)模型描述粘弹性涂层材料特性,以其感兴趣频率范围内的特征值作为目标函数,优化了涂层厚度以及涂层分布。Kumar[60]等学者采用模态应变能法(Modal Strain Energy Method)选择阻尼约束层的位点,获得了比较理想的宽频带阻尼减振特性。Zheng[61]等学者基于罚函数的遗传算法,计算了无源约束层减振块的最优位置和长度。
硬涂层阻尼减振(Vibration Damping of Hard Coating)是近年来发展起来的减振措施,硬涂层阻尼减振的优化设计理论及方法的研究还不够充分。
1.5 研究内容
硬涂层薄板的阻尼特性及其振动特性分析,是涂层复合材料(Coating Composite Materials)的重要科学研究课题。从已有文献看,对于涂层复合结构的阻尼特性及振动问题缺少系统深入的研究。
本研究团队认为,硬涂层薄板的阻尼特性及其振动特性分析,需要研究的问题有二,一是需要准确获得硬涂层复合结构的力学特性参数(包括弹性模量和损耗因子),这是动力学设计与分析的前提;二是分析方法需要考虑材料各向异性、几何非线性导致的振动复杂性和强非线性,掌握薄板理论、涂层复合层板的力学理论、非线性动力学特性和复杂振动行为。只有在充分掌握上述机理的基础上,才有可能进行硬涂层强度、刚度和阻尼等的合理优化设计,实现硬涂层结构件的最佳振动抑制、延长疲劳寿命。
面向硬涂层薄板结构减振优化设计,本文旨在报告硬涂层-薄板阻尼特性、固有特性与复杂振动行为的学术研究成果,其主要内容如下。
【研究内容之一 】 虑及压痕基体效应的硬涂层各向同性力学特性参数辨识方法和硬涂层材料的横观各向同性力学特性参数辨识方法,将辨识结果应用于硬涂层基体复合材料结构的振动特性分析,通过对比实验测试结果与数值计算结果,验证和确认适用于振动分析的、合理的硬涂层材料力学特性参数。
【The Research content of A 】 Isotropic and transversely isotropic mechanical parameters considering substrate effect are obtained and applied to the analysis for vibration characteristics of hard coating-substrate composite structure. By comparision between numerical and experimental results, these parameters are verified and confirmed to be reasonable and applicable to vibration analysis.
【研究内容之二】 基于复合层板力学理论、各向异性有限元数值计算、样件实测等方法,获得硬涂层薄板固有特性的精确解和数值解,分析参数影响规律。
【The Research content of B】 Based on the laminate plate theory, anisotropic finite element calculation and actual measurement of specimen, analytical and numerical solutions of natural characteristics of hard coating plate are obtained. Then the effect law of several parameters is studied further.
【研究内容之三】 针对工程实践中经常发生的高阶共振疲劳破坏,在提出固有频率、阻尼比、振动幅值、振动应力、疲劳寿命等减振指标的基础上,选取悬臂钛合金板典型模态,采用数值计算与实验测试方法,分析硬涂层减振效果。
【The Research content of C】 For the high-cycle resonance fatigue failure frequently occurred during engineering practices, natural frequency, damping ratio, vibration amplitude, vibration stress and fatigue life are presented as the evaluation indexes. Then two typical modes of cantilevered plate are selected for analyzing the damping effect by numerical calculation and experiment.
【研究内容之四】 基于等效非线性弹性薄板理论,建立硬涂层薄板的非线性振动方程,进行非线性摄动分析,寻找悬臂硬涂层薄板固有特性的近似解析解。
【The Research content of D】 Nonlinear vibration equations of hard coating-thin plate are deducted based on the theory of equivalent nonlinear elastic thin plate. The approximate analytical solutions of its natural frequencies are obtained by nonlinear perturbation analysis.
【研究内容之五】 虑及硬涂层薄板的几何大变形本构关系,基于Von Karman理论和Reddy三阶剪切变形理论,利用Hamilton变分原理建立硬涂层薄板的非线性动力学方程;利用Galerkin离散法对偏微分方程进行离散,建立硬涂层薄板横向变形的非线性控制方程;对横向谐波基础激励作用下的悬臂矩形钛合金薄板和悬臂硬涂层薄板非线性振动响应进行测试分析。
【The Research content of E】 Considering the geometrical large distortion constitutive relation, nonlinear vibration equations of hard coating-thin plate are deducted by Hamilton variational principle, based on Von Karman theory and three order distortion theory of Reddy. Then the partial differential equations are dispersed by Galerkin method to be the nonlinear governing equation of transverse deformation. The nonlinear vibration response under transverse harmonic base excitation of the bare and coated plate is measured.
【研究内容之六】 采用硬涂层对薄板结构阻尼减振的优化设计方法,将硬涂层薄板综合阻尼能力定义为优化设计目标,将涂层力学参数(弹性模量、损耗因子)和涂敷厚度等参数定义为设计变量,建构基于Reuss模型的优化设计流程,对硬涂层的弹性模量、损耗因子,以及涂敷厚度进行寻优,利用有限元法对最优参数进行减振效果的对比验证。
【The Research content of F】 By defining the comprehensive damping capacity as optimization target, mechanical parameters(elastic modulus and loss factors) and thickness as design variables,design optimization flow based on Reuss model is built, and consequently the optimal elastic modulus, loss factors and thickness are obtained. The optimal parameters are substituted into the dynamic model to verify the damping effect at last.
本文研究框架见图3。
2 硬涂层材料的力学特性参数辨识
2.1 基于纳米压痕实验的硬涂层各向同性力学特性参数辨识
由于制备工艺导致的不同微观结构,涂层材料的力学特性测试及表征,与块体材料相比,具有很大差异。
(1)对于无基体支撑的涂层,由于在取样和力学性能测试过程中容易发生破坏,导致独立涂层样品制备比较困难;
(2)对于有基体支撑的涂层,由于基体的存在以及基体与涂层之间界面的相互作用,测试结果难免会受到一定程度的影响;
(3)由于涂层的微小尺度,应用于块体材料的标准测试方法(如拉伸、压缩、弯曲,等等),已不再适用。

图3 硬涂层-薄板的阻尼特性、振动与优化设计研究架构Fig.3 Theoretical framework of the damping characteristics, vibration of hard-coating thin plate and optimization design
杨氏模量(Youngs Modulus)是一个描述材料弹性刚度的力学参数,表征了外部载荷(导致初始裂纹和微观断裂的产生)引起的弹性,对于接触应力场(Contact Stress Field)、涂层剥离、断裂和涂层内部残余应力状态有重要影响。一般认为,涂层对热冲击的抗力取决于杨氏模量。
本研究旨在将硬涂层简化为各向同性弹性材料,以弹性各向同性涂层-基体复合结构压痕过程的加载曲线为出发点,通过无量纲分析和有限元模拟,得到由加载曲线指数、最大加载力与材料力学参数、压痕深度组成的无量纲方程;在此基础上,结合纳米压痕实验得到的加载曲线,求解计及基体效应的涂层材料弹性力学参数,与Oliver和Pharr方法得到的等效模量值进行对比,验证采用有限元模拟与纳米压痕实验相结合辨识涂层材料力学参数的合理性和正确性。
2.1.1 涂层-基体复合结构的纳米压痕加载的无量纲方程
涂层-基体复合结构是由具有不同力学特性的两种材料组成,当压头压入涂层-基体复合结构时,压头附近涂层内的应力和应变的状态会因基体的存在而受到影响。
随着压痕深度的增加,压痕曲线中的信息实际上包含了涂层和基体等两种材料的特性。基体对压痕响应过程的影响称为基体效应(Substrate Effect)。
从有限元模拟的不同压入深度下压头附近及界面处的弹性应变分布(见图4)可以看出,当压痕深度超过一定范围之后,由压头压入涂层产生的应变已经扩展到了基体,并且在界面处不连续。
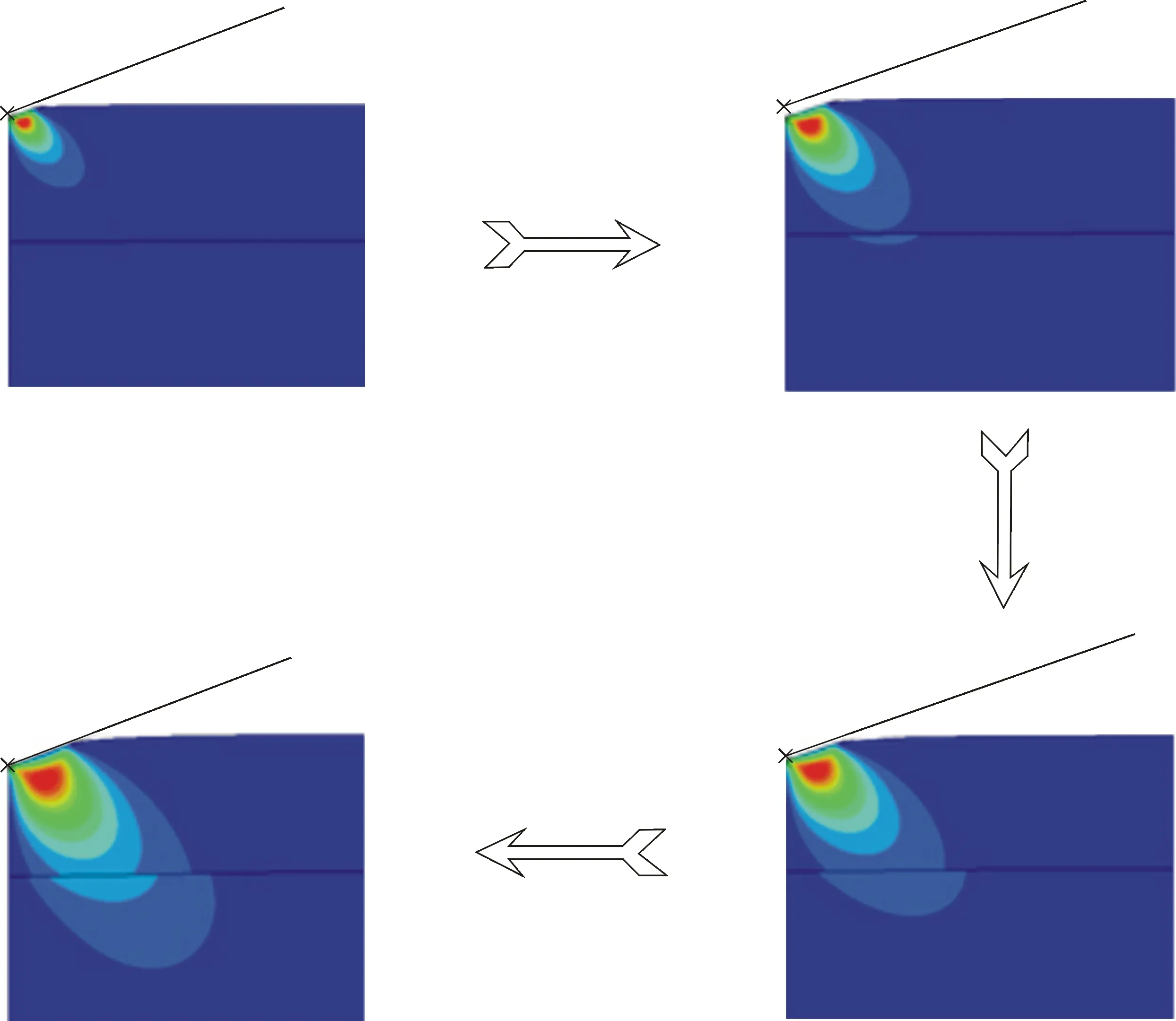
图4 不同压入深度下的弹性应变分布Fig.4 Distribution of elastic strains under different indention depths
由于基体效应的存在,在涂层-基体复合结构压痕的加载过程中,加载力与压痕深度的关系可以用幂指数函数模型进行修正[62]。
(1)
式中,F为加载力;Fmax为最大加载力;h为压痕深度;hmax为最大压入深度;χ为加载曲线指数。
加载曲线量化了压痕加载过程中基体对于涂层内应力状态的影响,即基体效应的大小。
涂层-基体复合结构的力学特性参数(ES,EC,νS,νC)、几何参数(主要是涂层厚度hC)、最大压痕深度hmax,都会对加载曲线产生影响。
基体和涂层材料的泊松比对压痕响应的影响比较小[63],常常被定为已知参数,在本文中,规定νC=νS=0.3。
Fmax可以写成如下形式:
Fmax=Φ*(ES,EC,hC,hmax)
(2)
式中,ES为基体杨氏模量;EC为涂层杨氏模量;hC为涂层厚度。
χ可以表示为如下形式:
χ=φ*(EC,ES,hC,hmax)
(3)
选用[L-M-T]作为基本量度单位。由于基体的杨氏模量ES和涂层厚度hC通常是已知的,故取ES和hC为基本量,则其余的量纲可用ES和hC的量纲表示为如下形式:
[Fmax]=[ES]1[hC]2
[χ]=[ES]0[hC]0
[EC]=[ES]1[hC]0
[hmax]=[ES]0[hC]1
(4)
式中,[ ]为参量量纲。
应用∏定理,可得
(5)
式中,ΠFmax为Fmax的无量纲化形式;其余依次类推。
则式(2)和式(3)可表示为以下无量纲形式。
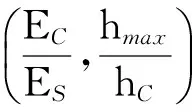
(6)
(7)
2.1.2 纳米压痕加载过程的有限元模拟
【step1】 使用弹性模量为1 140 GPa的Berkovich金刚石压头进行压痕实验,在建模时用半锥角为70.3°的圆锥压头来代替[64]。相对于被压试件材料,1 140 GPa的弹性模量,其量级已非常高,故将Berkovich金刚石压头等效为刚体,在ABAQUS中设置为Analytical rigid。
【step2】 圆锥压头压入试件的过程具有典型的轴对称特点,故采用轴对称的二维模型来模拟纳米压痕加载过程。
【step3】 采用四节点轴对称线性减缩积分单元(CAX4R)对涂层及基体进行网格划分,在ABAQUS中建立压头与涂层-基体复合结构有限元模型(见图5)。
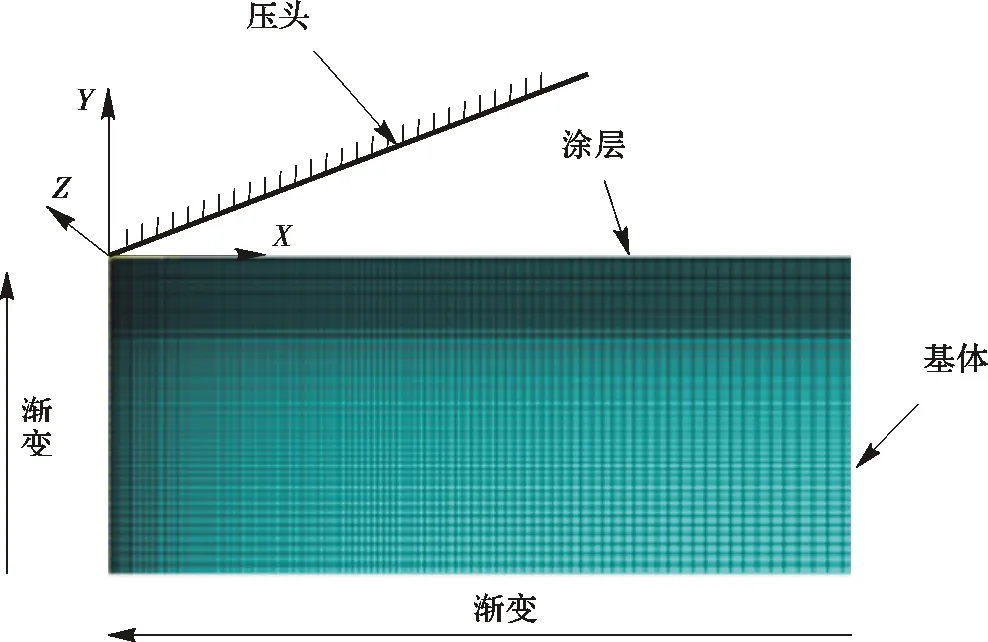
图5 涂层-基体复合结构压痕的有限元模型Fig.5 Finite element model of coating-substrate indentation composite structure
【step4】 约束基体下表面节点的所有自由度,压头只有向下的一个自由度,涂层的下边界和基体的上边界采用绑定约束(Tie)。创建压头和涂层材料之间的接触关系,设置刚性压头的压力面为主面,涂层的上表面为从面。


图6 模拟压痕加载过程中的压头位移和承受的反作用力Fig.6 Displacement and reaction force of the indenter in loading process
【step7】 提取每个载荷步对应的压头位移和作用在压头上的反作用力,即可绘制出有限元模拟的载荷-位移曲线。
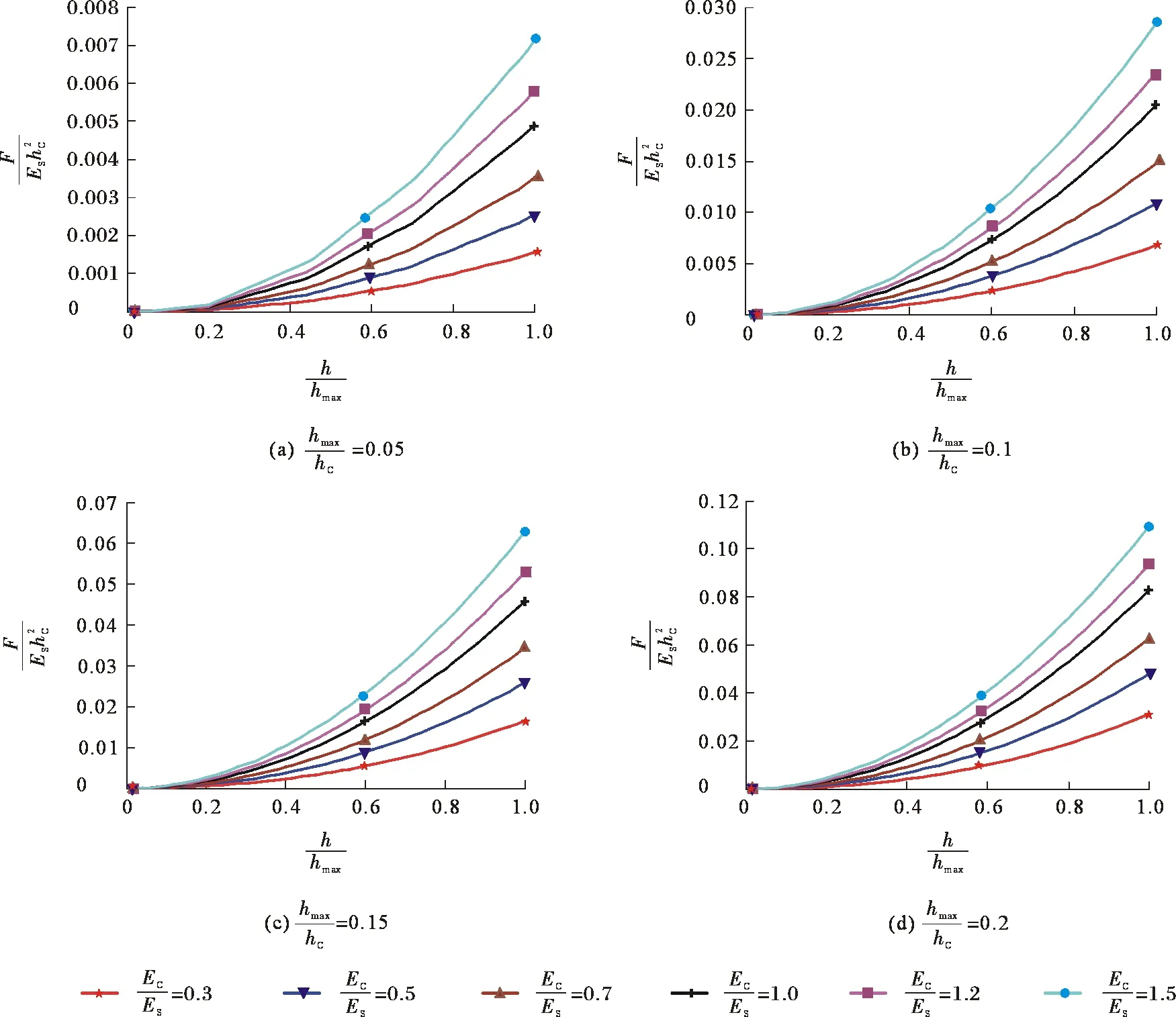
图7 不同的相对压入深度下得到的无量纲压痕加载曲线Fig.7 Dimensionless loading response curves under different penetration depths



(8)
式(8)涉及的相关系数值见表1。

表1 式(8)中的系数值Tab.1 The coefficients in Eq.(8)
由式(8)可知,在基体杨氏模量ES和涂层厚度hC已知的前提下,只要获得了最大压痕深度hmax和压痕响应的加载指数χ的值,就可以求出虑及基体效应的涂层杨氏模量EC。
(9)


(10a)
(10b)
式中,b1~b6为系数。
结合式(9)及式(10a)、式(10b),式(6)可以写成如下形式:
(11)
式(11)涉及的相关系数值见表2。

表2 式(11)中的系数值Tab.2 The coefficients in Eq.(11)
【step11】 根据式(11),在基体杨氏模量ES和涂层厚度hC已知的前提下,当确定了最大压入深度hmax和最大加载力Fmax,即可求出涂层的杨氏模量。
2.1.3 纳米压痕实验
基体材料:304不锈钢梁;
基体尺寸:60 mm×10 mm×1.8 mm;
材料参数:ρ=8×103kg/m3,E=193 GPa,ν=0.3;
处理工艺:钢梁表面抛光,保证具有良好的光洁度和导电性;
涂层靶材:NiCrAlY粉末;
有效成分:Ni75w%Cr19w%Al4w%Y2w%;
制备设备:FMA 90/80过滤电弧离子镀膜机;
制备工艺:EB-PVD;
涂层厚度:20 μm;
压痕仪器:CSM Nanoscratch Tester;
载荷范围:0~500 mN;
载荷分辨率:40 mN;
最大压入深度:200 μm;
位移分辨率:0.004 nm。
根据压痕实验过程记录的连续位移和载荷,绘制出5个测点的载荷-位移曲线(见图8)。
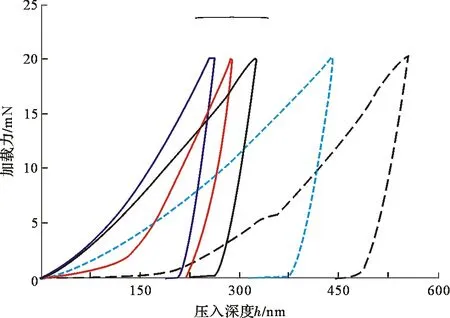
图8 NiCrAlY-不锈钢梁复合结构的压痕载荷-位移曲线Fig.8 The experimental load versus depth curves of coated beam
对较为相近的3次结果做平均处理,得到平均的位移-加载曲线(见图9)。

图9 平均载荷-位移曲线Fig.9 The average load versus depth curve
从图9可以读出,Fmax=20.02 mN,hmax=256.3 nm。对载荷-位移曲线的加载阶段进行拟合,得到χ=2.076。
根据Oliver[65]等学者的研究,被压试件的杨氏模量可以通过式(12)求解得到。
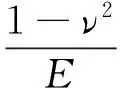
(12)
式中,Em为压痕模量(又称约化杨氏模量);E为样品的杨氏模量;ν为样品的泊松比;Ei为压头的杨氏模量,对于金刚石压头,Ei=1 141 GPa;νi为压头的泊松比,对于金刚石压头,νi=0.07。
式(12)中的压痕模量Em可以通过式(13)计算得到[66]。

(13)
式中,k为纳米压痕实验卸载曲线上部的斜率,即测得的刚度值;Em为压痕模量;A0为压头与样品弹性接触的投影面积。
当压头的几何形状已知时,投影接触面积是压痕接触深度的函数。对于理想情况下的Berkovich压头,接触投影面积A0由式(14)给出。
(14)
式中,hco为接触压痕深度。
一般地,可以认为

(15)
式中,ε为跟压头形状有关的参数,对于本实验使用的Berkovich金刚石压头,ε=0.76。

2.1.4 考虑基体效应的涂层材料力学特性参数确定
通过纳米压痕实验可以得到压痕加载曲线指数χ、最大加载力Fmax、最大压痕深度hmax,当基体杨氏模量ES已知时,将其代入式(8)和式(11),即可求得涂层的杨氏模量。
将Fmax=20.02 mN,χ=2.076,hmax=256.3 nm代入式(8)和式(11),求得涂层材料的杨氏模量,列入表3,同时,为了比较3种方法得到模量值,将Oliver方法[65]得到的经典模量值也列入表3。

表3 不同方法得到的涂层杨氏模量值Tab.3 Young’s modulus obtained by three methods
2.2 基于纳米压痕的硬涂层材料横观各向同性力学特性参数辨识
在许多工程分析场合,可以将涂层材料简化为各向同性线性材料。例如,美国材料协会(ASTM)提出的涂层材料力学特性标准测试方法[68],其测试前提就是假设涂层材料各向同性和线性。然而,硬涂层力学特性表现为各向异性,考虑其薄膜效应(Membrane Effect),可以将其视为横观各向同性,即在与基体平行的平面内具有相同的力学特性,在垂直于基体表面方向上的力学特性与各向同性面内的力学特性参数差异比较大[69]。
纳米压痕实验本身得不到任何关于涂层力学特性参数的各向异性特征。因此,在纳米压痕实验的基础上,将以NiCrAlY涂层为代表硬涂层,视为横观各向同性弹性体,通过模型简化,确定所要求解的独立力学特性参数(ET和EL),应用无量纲分析和有限元模拟,得到压痕响应过程中的最大加载力、加载曲线指数与硬涂层力学特性参数(ET和EL)之间的无量纲方程,通过与纳米压痕实验结合,对其横观各向同性材料参数进行求解。
2.2.1 硬涂层各向异性材料本构方程与横观各向同性模型
对于一般的各向异性弹性体,在小变形情况下,应力与应变成线性关系,可以表示为如下形式:
σ=cε
(16)
式中,σ为应力向量;ε为应变向量;c为弹性系数矩阵。
σ=[σ1,σ2,σ3,τ23,τ31,τ12]T
(17a)
ε=[ε1,ε2,ε3,γ23,γ31,γ12]T
(17b)
如果弹性体具有3个弹性对称面,则称其为正交各向异性弹性体,其弹性矩阵可以表述为如下形式:
(18)
从式(18)可以看出,正交各向异性弹性体的独立弹性常数只有9个。当坐标轴方向与弹性主方向一致时,正应力只与正应变有关,切应力只与对应的切应变有关,因此,拉压与剪切之间,以及不同平面内的切应力与切应变之间,不存在耦合作用。
【定义 横观各向同性弹性体】 在正交各向异性的基础上,如果物体内每一点都有一个弹性对称轴,也就是说,每一点都有一个各向同性平面,在这个平面内,沿各个方向具有相同的弹性。
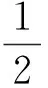
(19)
工程上常使用柔度矩阵形式[70]:
(20)
式中,L表示纵向(Longitudinal);T表示横向(Transverse);GL为横向面内的纵向剪切模量;GT为横向面内的横向剪切模量。
泊松比νLT和νTL满足如下形式:

(21)
式中,ET为横向杨氏模量;EL为纵向杨氏模量;νLT表示由横观各向同性面内应力导致的纵向应变与横观各向同性面内应变的比值;νTL表示由纵向应力导致的横观各向同性面内应变与纵向应变的比值。
横向面内的剪切模量可表示为如下形式:

(22)
式中,GT为横向面内剪切模量;νT为横向面内泊松比。
由于泊松比对计算结果影响较小,近似的取涂层材料各向同性面内的泊松比νT=0.3,另外的两个泊松比假设具有如下约束关系[43]:
νTL+νLT=2νT
(23)
根据文献[71],可以将纵向剪切模量近似地表示为如下形式:
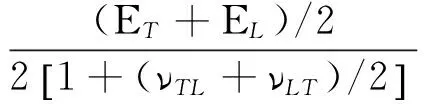
(24)
这样,所需求解的独立的弹性力学参数只剩下ET和EL两个。
根据Vlassaka[72-73]等学者的研究,各向异性材料的压痕模量为各个不同方向杨氏模量的加权平均,故而本文将压痕模量(Indentation Modulus)表示为如下形式:
Em=αET+βEL
(25)
式中,α和β为权系数,且α+β=1。
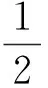
2.2.2 横观各向同性涂层-基体复合结构纳米压痕加载的无量纲方程
最大加载力可以表述为涂层-基体复合结构的弹性力学参数与几何参数的函数关系。
Fmax=φ(ET,EL,ES,hC,hmax)
(26)
与最大加载力的处理方式相同,加载曲线指数χ可以写成如下形式:
χ=φ(ET,EL,ES,hC,hmax)
(27)
选取基体材料的杨氏模量ES和最大压痕深度hmax作为基本量,应用Π定理对式(26)和式(27)进行无量纲化,可以得到如下算式:

(28)
(29)
在数值模拟中,取固定的与压痕实验相同的最大压入深度,故而式(28)和式(29)可以表述为如下形式:

(30)
(31)
由是可知,只要得到固定比例压痕深度下的最大加载力Fmax和加载曲线指数χ,就可以通过解算方程得到横观各向同性涂层的ET和EL。
2.2.3 有限元模拟的加载曲线
在ABAQUS中建立压头与涂层-基体复合结构的有限元模型,对压头压入涂层的过程进行模拟。
对于各向异性材料,在ABAQUS中需要定义局部材料坐标系,对于二维轴对称部件,ABAQUS中的材料坐标系见图10[74]。

图10 ABAQUS中各向异性材料的坐标系Fig.10 Coordinate of anisotropic material in ABAQUS
根据ABAQUS中的材料坐标系定义,对于横观各向同性的材料,在ABAQUS中进行如下设置:
(32)
式中,E1、E2、E3分别表示图10中材料坐标系x1、x2、x3等3个方向上的弹性模量;Nu12表示x2方向应力引起的x1方向应变与x2方向应变的比值;Nu13表示x3方向应力引起的x1方向应变与x3方向应变的比值;Nu23表示x3方向应力引起的x2方向应变与x3方向应变的比值;G12表示x1-x2面内的剪切模量;G13表示x1-x3面内的剪切模量;G23表示x2-x3面内的剪切模量。
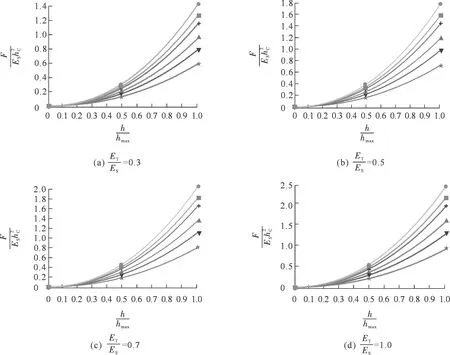




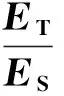
(33)
(34a)
(34b)
(34c)
为了表示方便,令
(35)
则无量纲最大加载力方程可表述为如下形式(系数见表4):
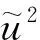
(36)
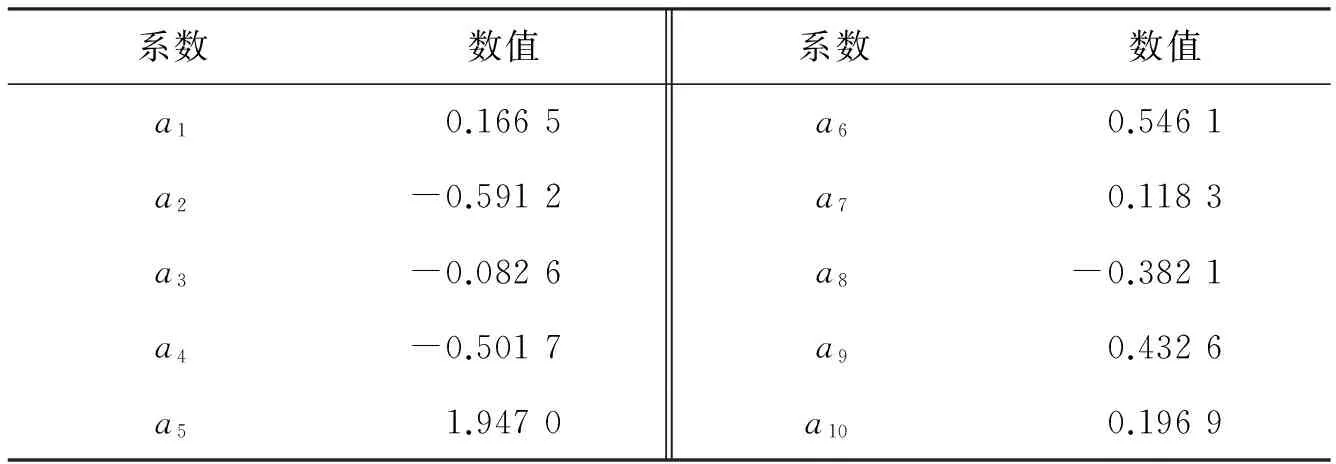
表4 式(36)中的系数Tab.4 The coefficients in Eq.(36)
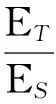
(37)
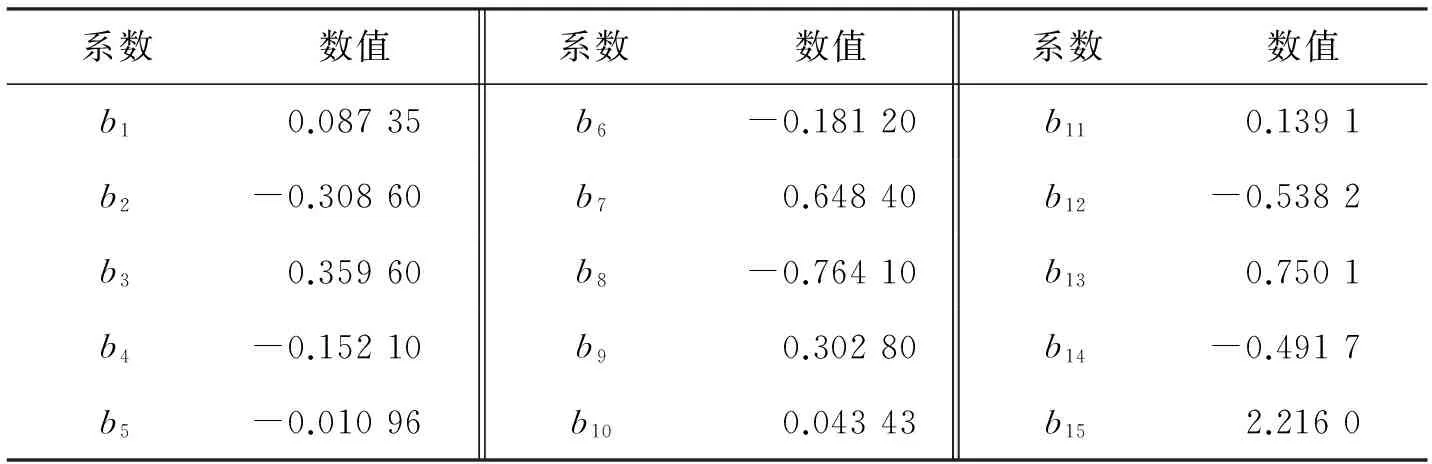
表5 式(37)中的系数Tab.5 The coefficients in Eq.(37)
2.2.4 基于纳米压痕实验的涂层材料横观各向同性力学参数的确定
将从纳米压痕实验中得到的压痕曲线提取的最大加载力Fmax、加载曲线指数χ和压痕模量Em,代入式(36)和式(37)进行求解。
由于对无量纲方程直接求解不便,采取定义目标函数的方法求其最优解。定义如下形式的目标函数:
(38)

表6 NiCrAlY涂层横观各向同性力学特性参数辨识结果Tab.6 Identification results of the transversly isotropic mechanical parameters of NiCrAlY coating
3 考虑各向异性的硬涂层-薄板复合结构的振动分析
在航空发动机压气机结构中,为应对叶片高周疲劳失效问题,硬涂层技术开始得到探索,其主要目标是在具备抗冲刷能力的同时,获得突出的阻尼减振功能。但是,支撑硬涂层技术实现的硬涂层-薄板复合结构(Hard Coating -Thin Plate Composite Structure)的振动动力学特性分析缺少深入研究。
硬涂层-薄板复合结构动力学特性分析方法(Analysis Method for Dynamic Characteristics of CP-Structure),必须考虑材料的各向异性及非线性因素;需要板理论、复合层板理论、各向异性弹性力学,以及非线性动力学等分析方法的共同支撑。只有掌握上述理论方法,才有可能进行硬涂层减振优化设计(Optimal Design of Hard Coating for Vibration Reduction),建构最佳的硬涂层-薄板结构件的功能和性能。
根据上述认识,拟以NiCrAlY涂层-钛合金薄板复合结构为对象,将辨识得到的各向同性与各向异性材料参数分别代入有限元模型,分析悬臂涂层板的固有特性和振动响应,对比两种力学特性参数得到的悬臂涂层板振动特性的异同;对涂层板的固有频率、模态阻尼比,以及第1阶(一弯)和第3阶(二弯)共振响应进行测试,对比计算和测试得到的固有频率值、共振响应值。
3.1 对象描述
选取TC4钛合金(Ti-6Al-4V)薄板作为基体[见图14(a)],采用EB-PVD在其表面单侧涂敷NiCrAlY涂层[见图14(b)],研究带有NiCrAlY涂层的钛合金薄板振动特性。结构的几何尺寸见表7,基体Ti-6Al-4V的材料参数见表8[75]。

图14 钛合金薄板以及涂层板Fig.14 Titanium alloy thin plate and coated plate

表7 薄板的尺寸及涂层厚度Tab.7 Dimensions and coating thickness of plate

表8 Ti-6Al-4V的材料参数[75]Tab.8 Material parameters of Ti-6Al-4V[75]
[注] 数据来自美国材料与试验协会(ASTM)的资料
通过用托盘天平称量涂层前后钛合金板的质量变化Δm,由涂层厚度、板的长和宽计算出涂层的体积,测得NiCrAlY涂层材料的密度为2 840.7 kg/m3。
3.2 基于有限元法的硬涂层-薄板复合结构振动分析
3.2.1 有限元模型
本研究采用Solid95单元模拟钛合金板,采用Shell 181单元模拟硬涂层。
对于各向异性弹性材料,ANSYS中有极端各向异性材料模型和正交各向异性材料模型,前者通过输入弹性系数矩阵来实现,后者通过定义不同方向的模量和泊松比来实现。
需要注意的是,各向异性材料参数的输入需要考虑单元坐标系的方向。对于Shell181单元,其默认的单元坐标系为X和Y轴在单元平面内,Z轴指向单元平面的法向。
对应本文中的横观各向同性材料,X-Y面为各向同性面。在ANSYS中NiCrAlY涂层材料参数进行如下设定:
(39)
式中,EX为X方向的杨氏模量;EY为Y方向的杨氏模量;EZ为Z方向的杨氏模量;GXZ为XZ面内的剪切模量;GYZ为YZ面内的剪切模量;GXY为XY面内的剪切模量;νXY为XY面内的泊松比;νXZ为XZ面内的泊松比;νYZ为YZ面内的泊松比。
涂层与基体的界面结合品质直接影响到涂层-基体复合结构的力学性能。Kerans[76]等学者将界面区域(Interface Area)分为突变型(Mutant Type)、化合物型(Compound Type)和扩散型(Diffuse Type)等3种。
采用EB-PVD制备涂层时,涂层靶材蒸发后作为带正电荷的高能离子,在高压阴极(基体)的吸引下,高速注射到基体表面,在基体上形成一种附着牢固的扩散镀层,而不是单纯的附着关系[77]。
因为EB-PVD制备的涂层与基体之间结合紧密,没有明显的界面层,并且涂层与基体界面之间有互熔现象,结合状态良好。所以本文不考虑涂层与基体薄板之间界面的影响,即假设涂层与基体界面处位移和应力是连续的,在ANSYS中采用合并重合单元、节点和关键点的方式将涂层绑定在基体上。
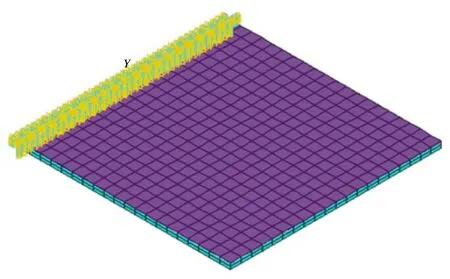
约束薄板底部全部方向的自由度,模拟悬臂条件,建立涂层-薄板复合结构有限元模型(见图15)。

图15 悬臂涂层-薄板复合结构的有限元模型Fig.15 Finite element model of cantilever coating-plate composite structure
3.2.2 硬涂层-薄板复合结构的固有特性分析
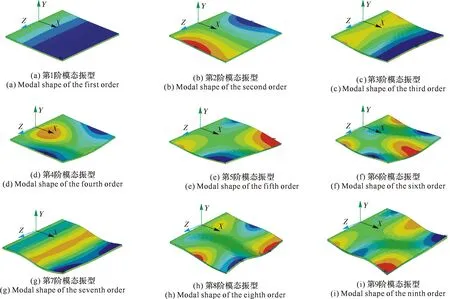
针对建立的涂层-薄板复合结构有限元模型,在ANSYS中采用Block Lanczos进行模态分析,提取涂层-薄板复合结构前10阶固有频率及模态振型。为了对比,采用辨识得到的两种材料力学参数进行计算分析,得到前10阶振型(见图16)。
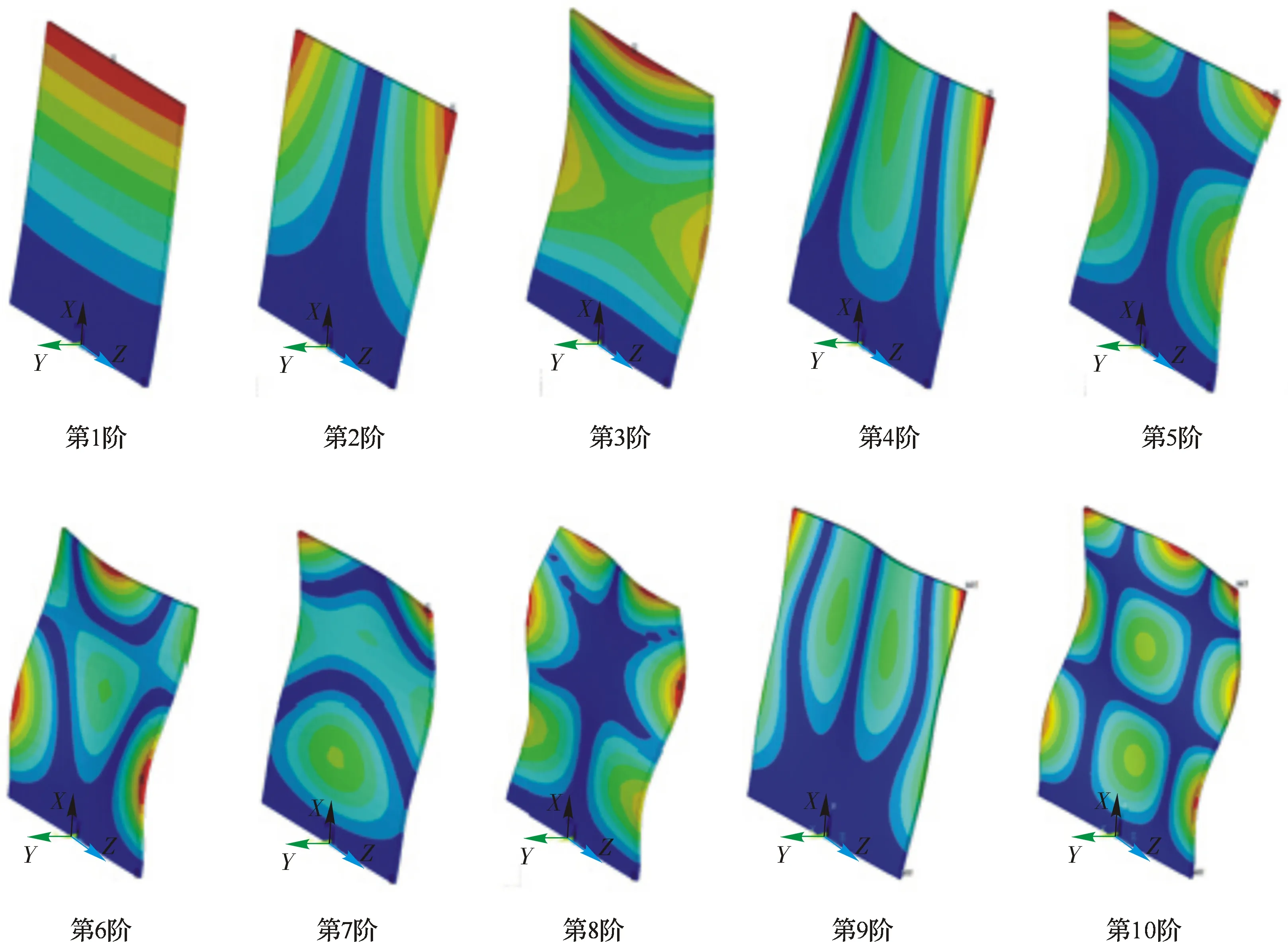
图16 有限元分析得到的前10阶模态振型Fig.16 The first 10 modal shapes obtained by finite element analysis
采用辨识得到的横观各向同性参数(Transversly Isotropic Mechanical Parameter)和采用各向同性材料参数(Isotropic Parameter)计算得到的涂层-薄板复合结构的前10阶固有频率(见表9),可以看出两种计算结果非常相近,但是采用辨识得到的各向同性材料参数比采用横观各向同性材料参数计算得到的结果普遍偏大。
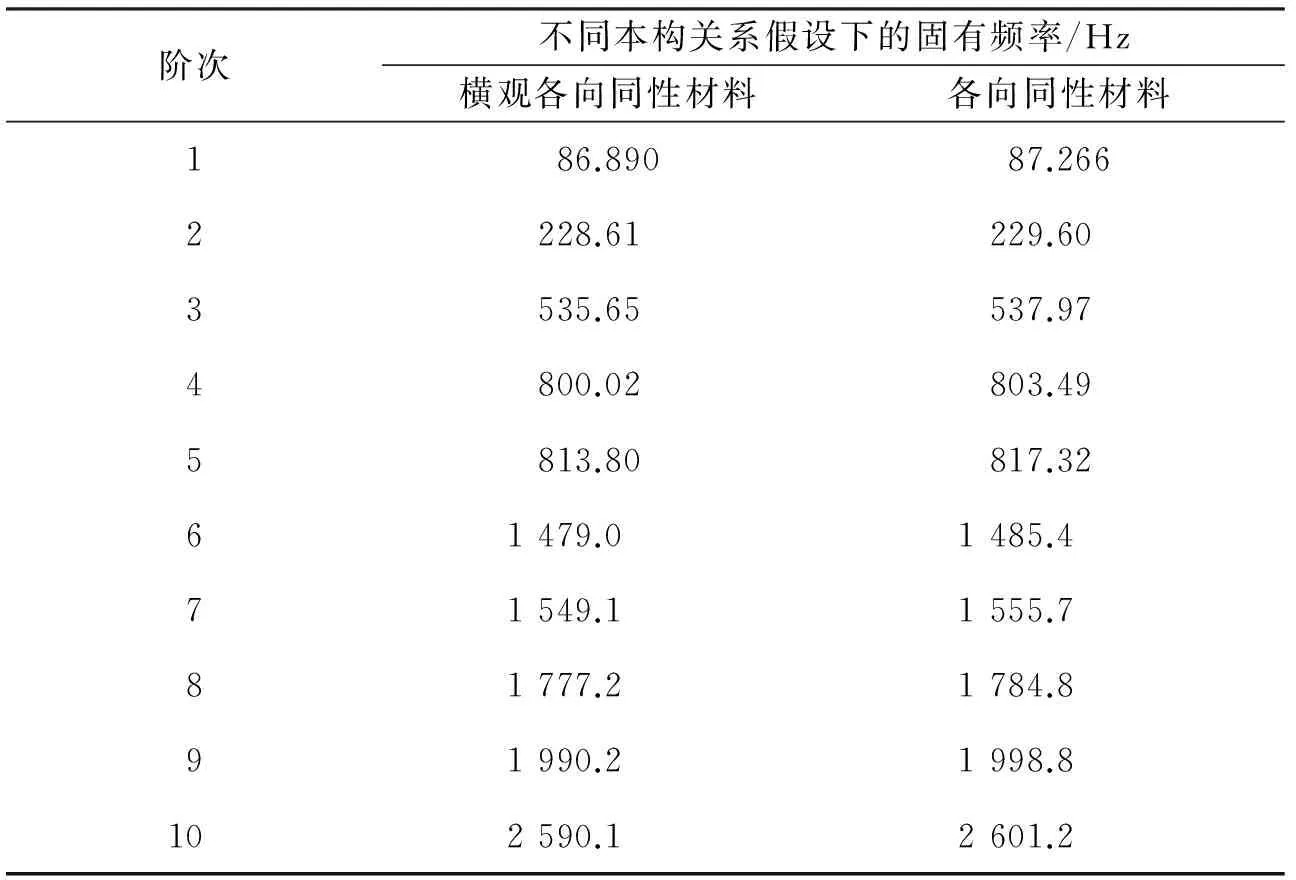
表9 有限元分析得到的涂层板前10阶固有频率Tab.9 The first 10 natural frequencies obtained by finite element analysis
3.2.3 硬涂层-薄板复合结构的响应分析
谐响应分析(Harmonic Response Analysis)用于确定线性结构在承受简谐载荷时的稳态响应,其目的是计算出结构在一定频率范围内的响应(包括位移、应力等),并得到响应对频率的曲线,从谐响应曲线上可以找到响应的“峰值”,并进一步得到峰值对应的位移和应力,可以帮助设计人员预测结构的持续动力学特性,验证结构能否成功地克服共振、疲劳,及其他受迫振动引起的有害效果,因而是计算结构动位移(Dynamic Displacement of the Structure)和动应力(Dynamic Stress)的一种有效方法[78]。
阻尼是动力学分析中非常重要的参数,影响着动力学响应的衰减,对于谐响应分析十分重要。本文采用实验测试得到模态阻尼比(Modal Damping Ratio),以恒定阻尼比的形式输入。
取模态振型表现为弯曲的第1阶和第3阶,采用模态叠加法进行谐响应分析。对结构整体施加Y方向上1g加速度,模拟基础激励的形式。将辨识得到的各向同性材料参数和横观各向同性材料参数分别代入有限元模型,计算响应点的Y方向的振动位移(见图17),计算结果见图18和图19。

图17 响应提取点Fig.17 Response point on thin plate

图18 第1阶谐响应曲线Fig.18 The harmonic response curves of the 1st mode

图19 第3阶谐响应曲线Fig.19 The harmonic response curves of the 3rd mode
从图18和图19可见,采用辨识出的横观各向同性材料参数与采用各向同性材料参数计算得到的响应值基本一致,后续的响应预估中采用辨识得到的横观各向同性结果。
3.3 基于实验测试的硬涂层-薄板复合结构的振动分析
3.3.1 硬涂层-薄板复合结构的固有频率测试
采用振动台基础激励方式对硬涂层-薄板复合结构的固有频率进行测试(见图20)。采用振动台激励时,激励频率和幅度均为闭环控制,所以对激励源的控制精度非常高。另外,基础激励的能量大,能够充分引起试件振动,获得系统没有激振设备附加质量影响下的固有特性。

图20 固有频率测试系统Fig.20 The measurement system of natural frequencies
扫频测试时,必须采用足够缓慢的扫频速度,以保证结构处于稳态振动中,对于小阻尼系统,尤其应该注意这一点。按照文献[15]中的扫频速率准则进行扫频激励。
响应信号在连续时间范围内的自功率谱(自相关函数的傅立叶变换)开根号之后按时间顺序排列,组成瀑布图(见图21)。从瀑布图中可以看出各种频率的组成与振幅是如何随时间变化的。通过寻找瀑布图中振幅最大处所对应的频率,可精确获得结构的固有频率。
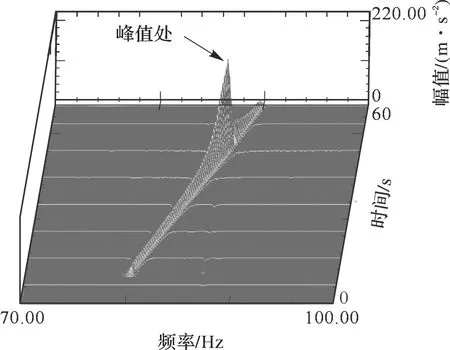
图21 扫频信号的瀑布图Fig.21 Waterfall plot of sweep frequency signal
由于硬涂层复合结构具有软式非线性特征,扫频时应采取从高到低的方式进行,以免无法得到固有频率处对应的峰值[15]。在扫频进行前,使用锤击法粗略获得结构的固有频率值,作为扫频频段的选择依据,最终得到NiCrAlY涂层板的前8阶固有频率(见表10)。

表10 NiCrAlY硬涂层-薄板的前8阶固有频率Tab.10 Natural frequencies of hard-coating thin plate
3.3.2 阻尼参数的辨识
由于实验观测到的硬涂层复合结构的非线性比较弱,本研究使用锤击法得到各阶频率响应函数曲线(见图22)。采用半功率带宽法(Half-Power Bandwidth Method)辨识各阶模态阻尼比,得到前10阶模态阻尼比(见表11)。
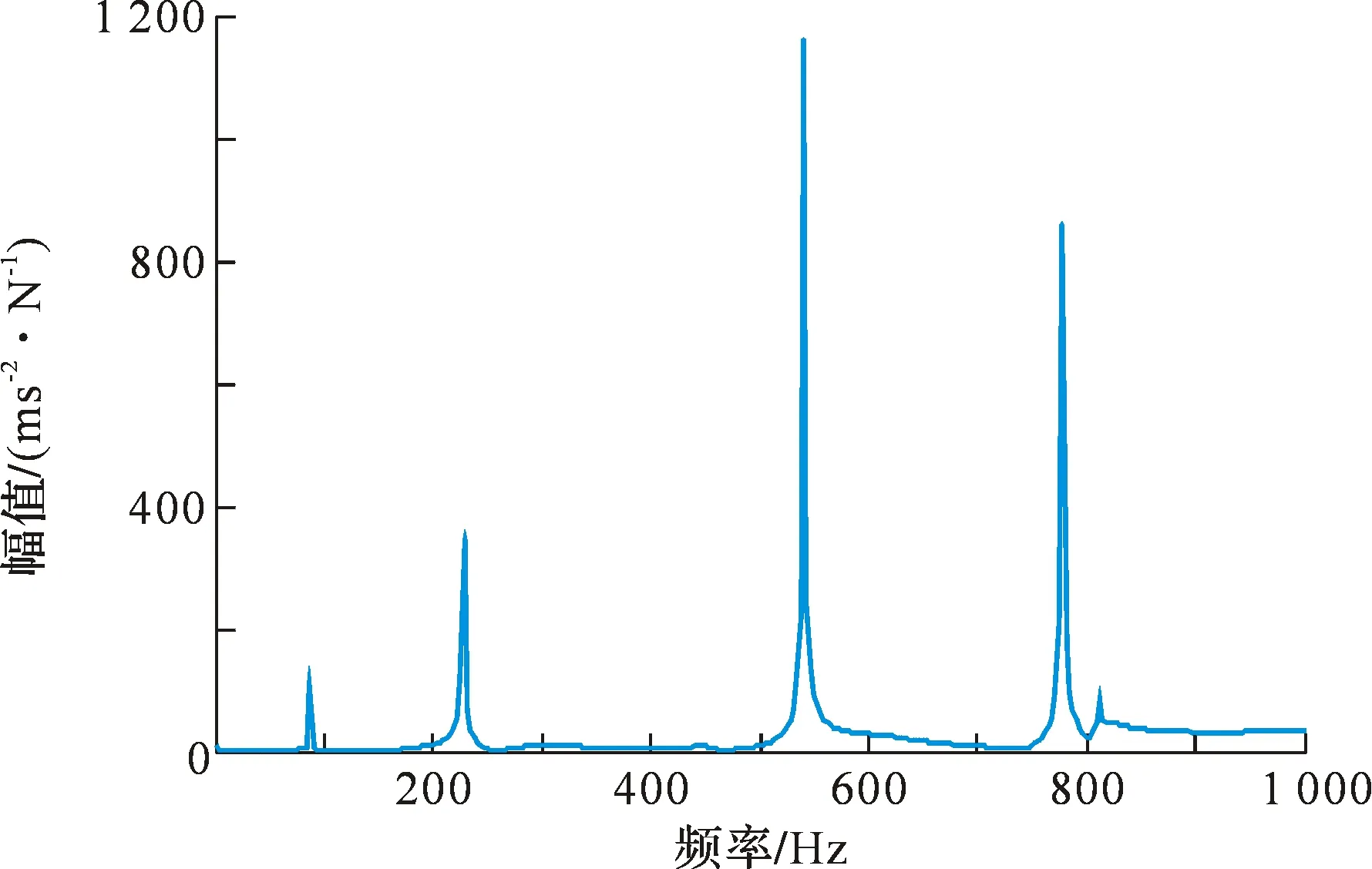
图22 锤击法得到的频响函数曲线Fig.22 FRF curves obtained by Hammering Method

表11 NiCrAlY硬涂层-薄板的前10阶阻尼比Tab.11 Damping ratio of the first 10 modes of hard-coating thin plate
3.3.3 振动响应的测试
以第1阶固有频率为激振频率,使用振动台以1g加速度幅值对悬臂涂层板进行定频激振,待其振动达到稳定状态时测试对应响应提取点(见图17)的加速度响应信号(见图23)。

图23 第1阶共振时域响应信号Fig.23 Time-domain response signal
从图23发现,第1阶共振测试得到的时域图形两侧不对称,正向信号出现了类似“削波”的情形。由于第1阶的模态振型为一弯,说明悬臂涂层钛板在涂层与未涂层两侧的弯曲振动加速度不同。
对时域信号做FFT,得到其频谱图(见图24),可以看出,频谱图中出现了激振力频率及其连续奇偶次高阶谐波分量,而且偶次倍频谐波分量相对奇次倍频谐波分量较小。
分析其原因,EB-PVD制备的涂层为柱状晶,当悬臂钛板向涂层侧弯曲时,柱状晶之间被压紧,刚度大;向未涂层侧弯曲时,柱状晶之间被拉开,刚度小;这造成了两侧的抗弯刚度不同。
由于实际观测常常是以位移的形式,经过两次积分,将加速度信号转换成位移信号(见图25)。

图24 第1阶固有频率激振得到的幅频特性曲线Fig.24 Frequency response curve of the 1st mode
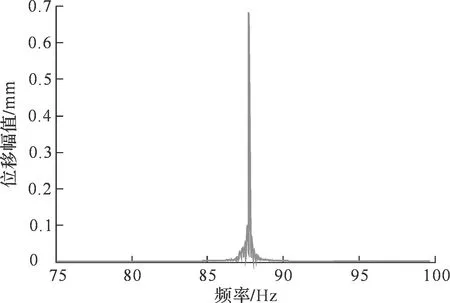
图25 1g加速度定频激励下第1阶共振响应Fig.25 Resonant response of the 1st mode at 1g dwell
3.4 有限元计算与实验结果对比分析
3.4.1 固有频率的对比及材料参数的验证
对比涂层-薄板复合结构的动力学测试与计算结果,验证材料参数与有限元模型的正确性,首先应保证基体钛合金板的计算和测试结果是正确一致的。测试得到钛合金板涂层前的前8阶固有频率与有限元计算结果(见表12),可以看出,除第7阶外,有限元计算和实验测试结果的差异率均小于2%,取得了很好的一致性,说明实验测试与有限元计算结果都是正确可信的。

表12 钛合金板的前8阶固有频率Tab.12 Natural frequencies of first 8 orders(bare plate)
通过实验测试与有限元计算得到的涂层板前8阶固有频率以及它们之间的差异率(见表13),为了更好地对比,将各阶固有频率的差异率绘制于图26。
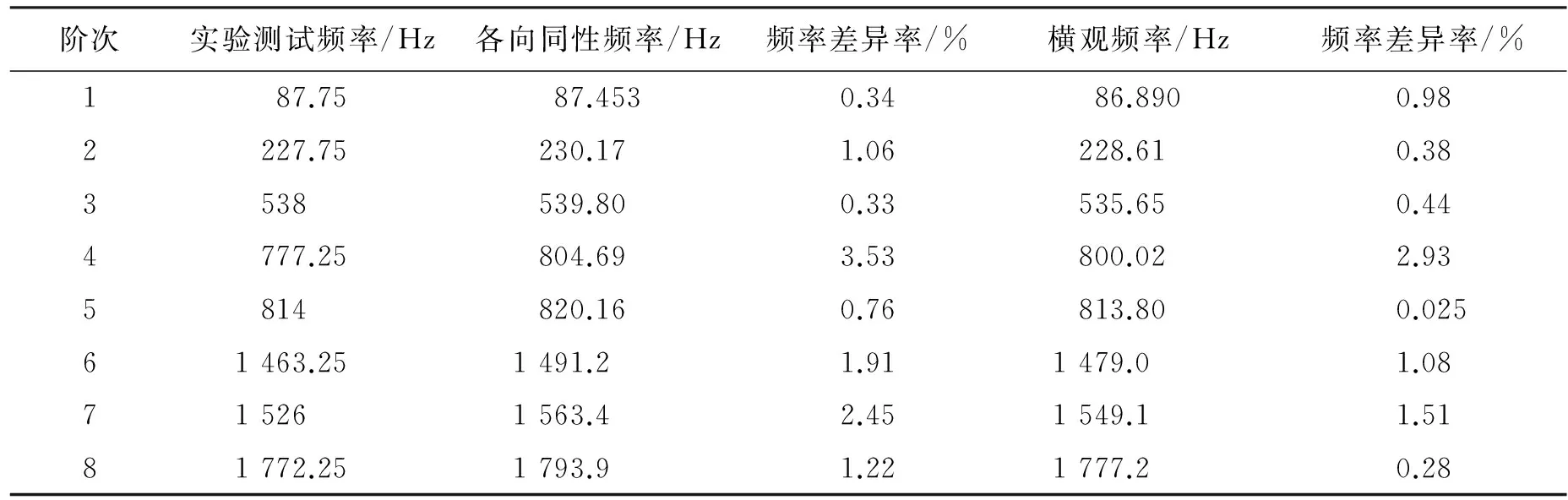
表13 涂层板的前8阶固有频率对比Tab.13 Natural frequencies of first 8 orders(coated plate)
从图26可以看出,采用辨识得到的各向同性材料参数与横观各向同性材料参数计算的固有频率结果与实验测试结果的差异率大部分在2%以下,而且采用横观各向同性材料参数计算的固有频率结果在高阶部分(图中4~8阶)与实验测试得到的结果更为接近。

图26 采用辨识得到的两种参数计算固有频率结果与实验结果差异率之对比Fig.26 Comparison of the difference ratio between the experimental results and FEM by two kinds of material parameter
3.4.2 共振响应的对比
由于实验测试时传感器的粘贴位置是一个区域,而不同于有限元计算中的一个节点,因此在计算时本研究取测点附近的9个点(见图27)拾取响应值,进行平均得到位移-频率曲线与实验测试得到的响应值。

图27 响应拾取点Fig.27 Nodes for extracting response
图28和图29分别为第1阶和第3阶通过有限元计算与实验测试得到的共振态位移响应。从结果对比来看,采用谐响应计算得到的响应值能够较好的预估涂层-薄板复合结构共振状态下的响应。

图28 第1阶共振响应测试结果与谐响应对比Fig.28 Comparison of 1st mode resonant responses between measurement and harmonic response analysis
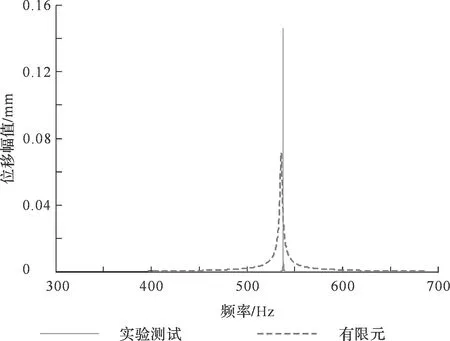
图29 第3阶共振响应测试结果与谐响应对比Fig.29 Comparison of 3rd mode resonant responses between measurement and harmonic response analysis
4 硬涂层减振有效性分析
在结构件上涂敷硬涂层,目的是降低结构件的振动响应,提高疲劳寿命。结构件振动响应、疲劳寿命与结构系统的动应力、振动幅值、阻尼参数、固有频率等因素相关,只有确定了上述因素的变化关系,才有可能有效地评价硬涂层的减振效果。
研究证实,引起悬臂钛板类结构件疲劳失效的一个重要来源模态是双条纹模态(two stripes mode)[4]。从悬臂钛板第4阶双条纹模态的振型与应力分布(见图30)可以看出,在第4阶模态振动下,悬臂钛板的最大应力值分布于远离固定端的自由端。相较根部而言,自由端采取加强措施比较困难。

图30 第4阶模态振型与应力Fig.30 Modal shape and stress distribution of the 4th modeIvancic
针对悬臂钛板的双条纹模态进行了研究,当采用电磁振动台对悬臂钛板在第4阶固有频率下进行1×106周激振后,用紫外线照射观测,发现悬臂钛板的自由端出现了裂纹(见图31);随后,再针对涂覆镁铝合金硬涂层后的悬臂钛板,采用第4阶固有频率进行激振,发现在5×106周时,悬臂钛板的自由端出现了类似裂纹,说明第4阶共振下的硬涂层-悬臂钛板疲劳寿命明显增大。
除第4阶双条纹模态之外,高阶振动在工程上带来的破坏也不容忽视[79-80]。从悬臂薄板第10阶模态振型与应力分布(见图32)可以看出,除了根部应力较大外,在远离固定端的一侧靠近叶尖处,对称地出现了两个应力较大区域,由于根部强化措施比较容易实现,该阶模态振动下的疲劳破坏往往会出现在顶端的两个应力较大区域。

图31 悬臂钛板发生疲劳破坏的位置[20]Fig.31 The location of fatigue failure on cantilever Titanium plate[20]
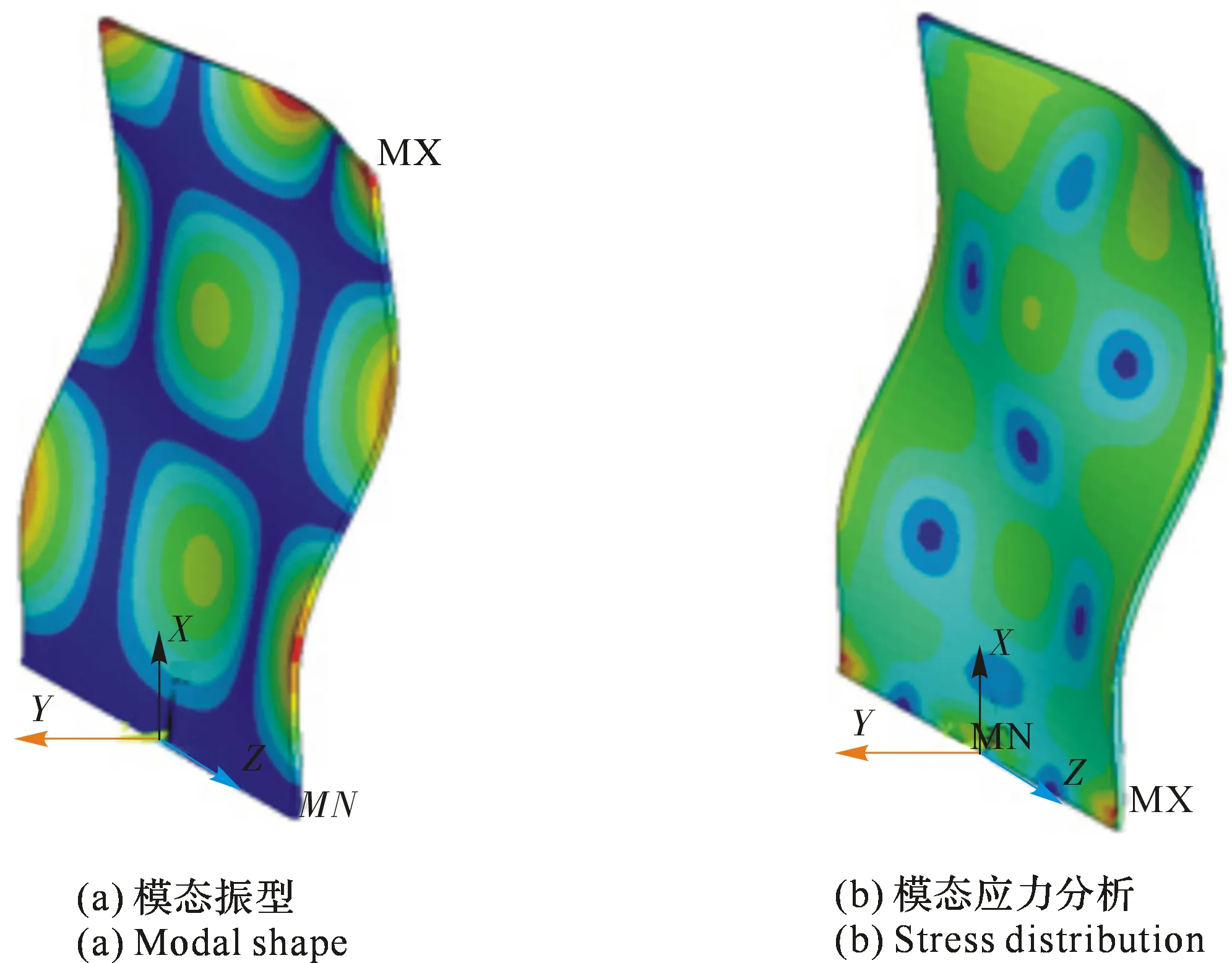
图32 第10阶模态振型与应力Fig.32 Modal shape and stress distribution of the 10th mode
针对工程中经常发生的高阶共振疲劳破坏,选取悬臂钛板的第4阶模态和第10阶模态,在建立减振指标的基础上,分析硬涂层的减振效果。
4.1 减振评价指标
为便于计算与测试,针对硬涂层-薄板结构与模型,选取以下参数作为硬涂层阻尼减振有效性评价指标(Effectiveness of Hard-Coating Damping,EH-CD)。
(1)固有频率变化(Variation of Natural Frequency) 涂敷硬涂层后,结构件的固有频率将可能发生变化,从而避开原始共振点。
(2)阻尼比(Damping Ratio) 从能量耗散的角度反映出硬涂层对于振动的抑制效果。
(3)振动幅值(Vibration Amplitude) 涂覆涂层前后,薄板在相同激励水平下的振动幅值若发生变化,将可以直观和有效地评价硬涂层的减振效果。
(4)振动应力(Vibration Stress) 结构件的疲劳寿命与应力、应变水平直接相关,通过计算涂层前后悬臂钛板应力分布,以及危险区域应力值等的变化,可以掌握其发生破坏的危险区域及应力水平,进而评估硬涂层的减振效果。
(5)疲劳寿命(Fatigue Life) 疲劳寿命的增大是抑制结构振动的最终目的,计算涂层前后悬臂钛板的振动疲劳寿命,是评价硬涂层减振效果的终极指标。
4.2 硬涂层对悬臂钛板固有特性的影响
观察有限元计算得到的涂层前后悬臂钛板的前10阶固有频率(见表14),可以看出,涂敷NiCrAlY涂层后,悬臂钛合金板的前10阶固有频率都有所上升。

表14 涂层前后悬臂钛合金板固有频率的变化Tab.14 The effect of coating on natural frequencies of NiCrAlY deposited on cantilever Titanium plate
采用半功率带宽法(Half-Power Bandwidth Method)得到了悬臂板涂覆涂层前后前8阶模态阻尼比(见表15)。

表15 悬臂钛板涂层前后的前8阶模态阻尼比Tab.15 Damping ratio of thin bare and coated Titanium plate
为了更清晰地观察阻尼比的变化,将涂层前后的模态阻尼比在图33中进行了对比,可以看出,涂层之后悬臂钛板的前8阶模态阻尼比除第3阶略有降低、第5阶基本不变外,其他各阶均有所上升。
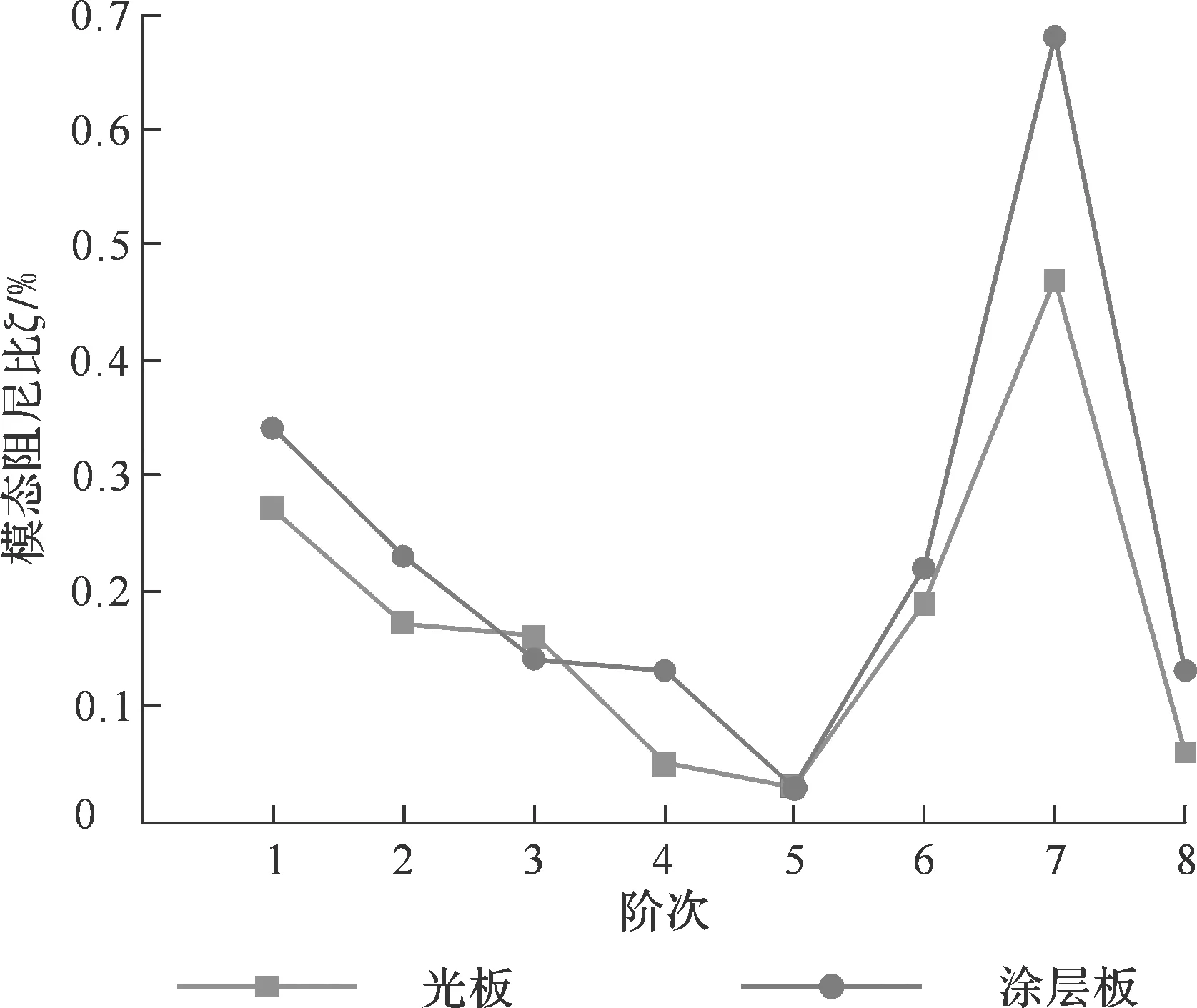
图33 涂层前后的前8阶模态阻尼比Fig.33 First 8 orders damping ratios of bare and coated plate
4.3 硬涂层对悬臂钛板振动位移与应力的影响
4.3.1 振动位移
采用模态叠加法(Mode Superposition Method,MSM)对悬臂钛板在第4阶和第10阶固有频率附近进行谐响应分析。采用基础激励,对薄板整体施加1g加速度激励。
根据悬臂钛板第4阶模态振型,在薄板的顶端(自由端)等距取11个节点(见图34),可以看出,该模态下振动位移最大点为节点No.11。

图34 第4阶模态振型及顶端节点编号Fig.34 The 4th order modal shape and node number on top side
提取节点No.11位移对频率的幅频特性曲线(见图35),可以看出,涂层后薄板的第4阶固有频率发生了偏移,该点振动位移明显下降。

图35 节点No.11拾取的涂层前后的谐响应曲线(第4阶)Fig.35 Harmonic response curves of node No.11(The 4th mode)
提取1g基础激励这11个节点的振动位移峰值(见图36)进行观察,可以发现,涂层后薄板自由端11个节点的振动位移均有下降。

图36 涂层前后第4阶谐响应计算得到的响应幅值Fig.36 Displacement amplitude of the 4th order resonance
同样地,采用基础激励,对悬臂钛板整体施加1g激励,在第10阶固有频率附近进行谐响应分析。根据悬臂钛板第10阶模态振型,可以看出,该模态下振动位移的最大点为节点No.11(见图37)。

图37 第10阶模态振型及顶端节点编号Fig.37 The 10th order modal shape and node number on top side
取该模态下最大振动位移点(节点No.11),提取该点位移对频率的幅频特性曲线(见图38)。可以看出,涂层后薄板的第10阶固有频率发生了偏移,该点振动位移明显下降。

图38 节点No.11拾取的涂层前后的谐响应曲线(第4阶)Fig.38 Harmonic response curves of the node No.11 corresponding to bare and coated plate
提取1g基础激励这11个节点的振动位移峰值(见图39),可以看出,谐响应计算得到的各节点振动位移能够反映悬臂钛板顶端的振动形式,涂覆涂层后,悬臂钛板自由端的这11个节点的振动位移均有下降。
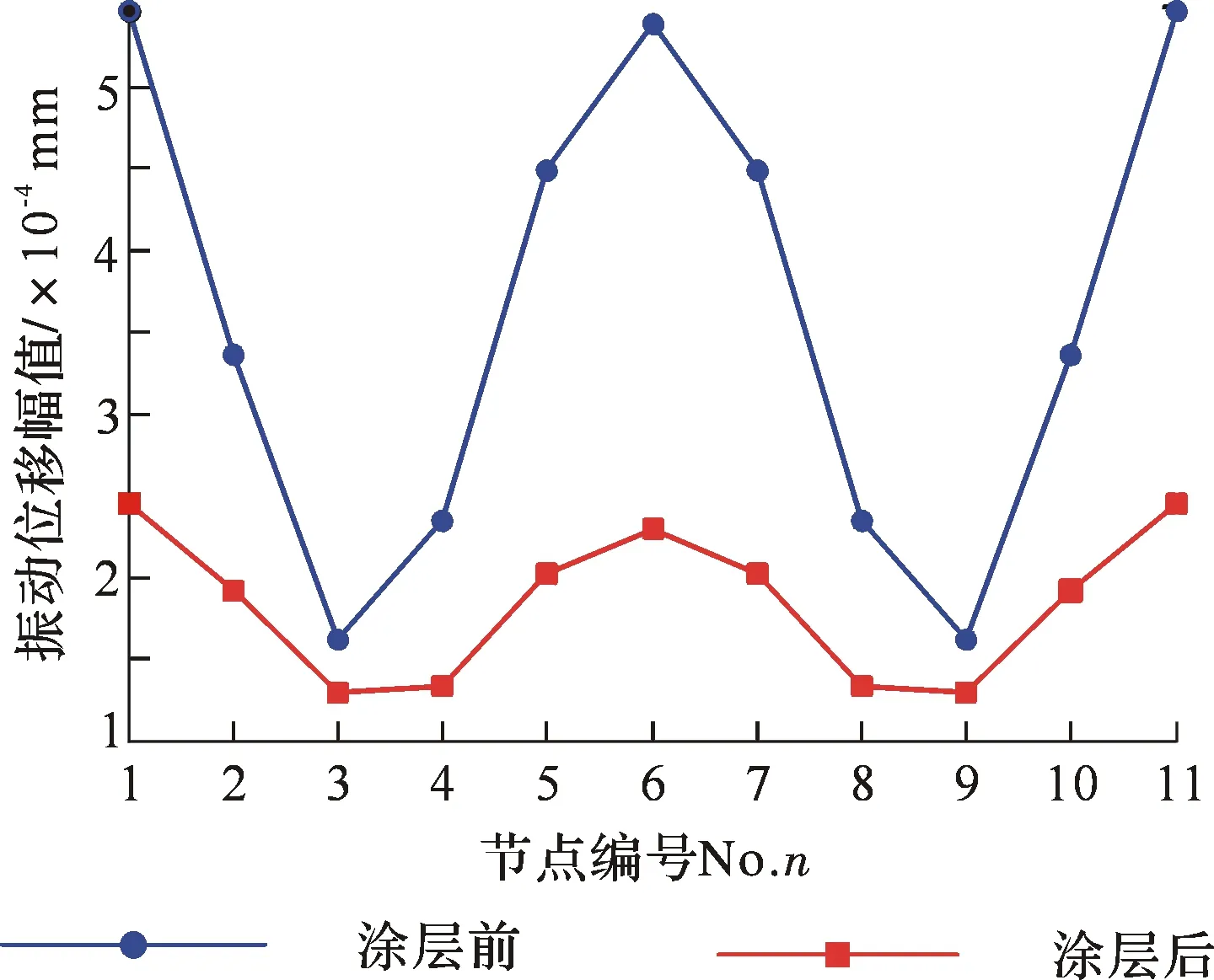
图39 薄板自由端各节点涂层前后的共振响应峰值Fig.39 Harmonic response curves of nodes on the free top edge corresponding to bare and coated plate
4.3.2 振动应力
疲劳破坏是机械零件失效的主要原因之一。据统计,大约有80%以上的机械零件失效属于疲劳破坏,而且疲劳破坏前没有明显的变形,因此,疲劳破坏经常造成重大事故[81]。
结构件疲劳与其应力有着直接相关性,疲劳破坏一般发生在应力较为集中的区域。因而,计算涂层前后结构件的振动应力,对评价硬涂层的减振效果具有十分重要的意义。
采用模态叠加法(MSM),对薄板整体施加1g基础激励,对悬臂钛板在第4阶固有频率和第10阶固有频率附近进行谐响应分析,计算其应力值。
根据悬臂钛板的模态应力的分布形式,取第4阶模态下振动应力的最大点(见图40节点No.6),提取该点等效应力对频率的幅频特性曲线(见图41),可以看出,涂层后该点应力值发生了大幅度下降。

图40 第4阶应力分布及顶端节点编号Fig.40 The 4th order stress distribution and node number on top side

图41 涂层前后节点No.6的等效应力Fig.41 Equivalent stress of node No.6 of bare and coated plate
进一步地,提取1g基础激励下这11个节点的振动位移峰值(见图42),可以看出,采用谐响应分析得到的各节点最大应力复合该阶次模态应力的分布形式,涂敷NiCrAlY涂层后,悬臂钛板顶端各节点的应力值均有大幅下降。

图42 涂层前后第4阶固有频率激振下的等效应力值Fig.42 Equivalent stress of the plate under excitation at the 4th natural frequency
根据悬臂钛板的第10阶模态应力的分布形式(见图43),取该模态下节点No.4,绘制其等效应力对频率的幅频特性曲线(见图44),可以看出其应力值发生了大幅度下降。

图43 第10阶应力分布及顶端节点编号Fig.43 The 10th order stress distribution and node number on top side
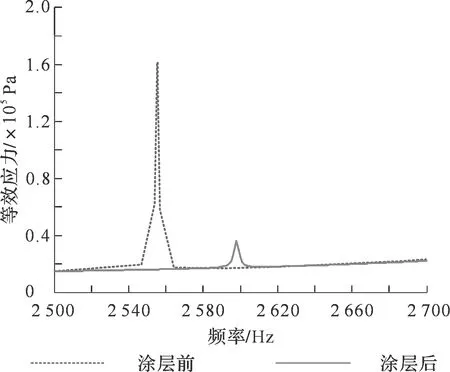
图44 谐响应分析得到的节点No.4的等效应力Fig.44 Equivalent stress of node No.4 obtained by harmonic response analysis
提取出悬臂钛板顶端各节点的最大等效应力值(见图45),可以看出,采用谐响应分析得到的各节点最大应力符合该阶次模态应力的分布形式,涂敷NiCrAlY涂层后,悬臂钛板顶端各节点的应力值均有大幅下降。

图45 第10阶固有频率激振下悬臂钛板上节点的最大等效应力Fig.45 The largest equivalent stress of different nodes on cantilever plate at the 10th natural frequency
4.4 硬涂层对悬臂钛板振动疲劳寿命的影响
结构件减振的最终目的是提高其疲劳寿命。疲劳破坏是一个累积损伤的过程,对于等幅交变应力,可用材料的S-N曲线来表示在不同用力水平下达到破坏所需要的循环次数。于是,对于给定的应力水平σ,就可利用材料或零部件的S-N曲线,确定该零件至破坏时的循环数N,估计出零件寿命。
对涂层前后的悬臂钛板进行30g基础激励,在第4阶固有频率附近进行谐响应分析,提取最大应力点的等效应力(见图46)。

图46 30g加速度基础激励下悬臂钛板第4阶共振的等效应力Fig.46 Equivalent stress of the cantilever plate under 30g acceleration
由于涂层的应力疲劳数据未知,在此仅报告钛合金板的疲劳,暂不考虑涂层的疲劳破坏。提取涂层前后悬臂钛板第4阶共振下的最大等效应力值,根据TC4在室温下的应力疲劳数据(见表16),采用线性插值法(Linear Interpolation Method)获得相应的对称循环应力下的循环寿命Ni(见表17)。

表16 TC4室温下的应力疲劳数据[82]Tab.16 Stress fatigue data of TC4 at room temperature[82]

表17 涂层前后第4阶固有频率30g激励下钛合金板的疲劳寿命Tab.17 Fatigue life of bare and coated plate at the level of 30g
对比涂层前后30g基础激励下悬臂钛板第4阶共振的疲劳寿命,涂层后钛板的疲劳寿命明显增大。
5 基于等效非线性弹性板理论的悬臂硬涂层-薄板固有特性分析
将硬涂层-薄板等效为非线性材料制作的弹性薄板,建立硬涂层-薄板非线性运动方程(Nonlinear Kinematic Equation of CP-struture);采用小参数法(Method of Small Parameter)求解其固有特性近似解;对照有限元计算、实验测试和固有特性近似解等相关结果,确认所建立的近似等效分析方法。
5.1 硬涂层-薄板等效为非线性弹性板的基本方程及其求解方法
5.1.1 基本方程
将材料梯度变化引起的弹性力学三维变系数方程组(Three-Dimensional Equations with Variable Coefficients)转化为二维各向异性常系数方程(Two-Dimensional Anisotropic Equations with Constant Coefficient)。若三维几何方程保持不变,根据薄板理论假定[83],得到各向同性弹性板(见图47)的位移分量。

(40)
式中,u为x方向的位移;v为y方向的位移;w为z方向的位移;t为时间。
应力分量可以表述为如下形式:

(41)
式中,εx为x方向正应变;εy为y方向正应变;γxy为剪切应变。

a为薄板长度;b为薄板宽度;h为薄板厚度;q(x,y,t)为面内横向外载。图47 各向同性弹性板Fig. 47 Isotropic elastic plate
根据材料非线性弹性薄板理论[84],由硬涂层-薄板等效的非线性弹性板应力-应变关系可表述为如下形式:
(42)
式中,σ为应力;ε为应变;E为初始弹性模量;B为材料非线性项系数,其值为正值;下标i可以取x,y和xy。
这样,等效非线性弹性板(The Equivalent Nonlinear Elastic Plate)的本构方程可表示为如下形式:
(43a)
(43b)
(43c)
式中,σx为x方向正应力;σy为y方向正应力;τxy为剪切应力。
相应的,等效非线性弹性板的内力分量可表述为如下形式:
(44a)
(44b)
(44c)
(44d)
(44e)

在板面横向外载q(x,y,t)作用下,由z方向的力平衡条件及x,y方向的力矩平衡条件,可得计入质量密度的三维动力平衡方程(Three-Dimensional Dynamic Balance Equations including Mass and Density)。

(45a)

(45b)
(45c)
(45d)
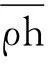
将式(45a)、(45b)代入式(45c),整理后代入式(44),可得等效非线性弹性板的非线性运动方程(Nonlinear Kinematic Equation of the Equivalent Nonlinear Elastic Plate)。
(46a)
(46b)

(46c)
5.1.2 方程求解
取式(46)的解为如下形式:
(47)
式中,w(x,y,t)为薄板中面任一点的挠度;w0(x,y)为满足等效非线性弹性板全部边界条件的挠度函数;S(t)为时间项。
根据Galerkin原理,结合式(46a),S(t)将满足如下形式:
(48)
式中,A为薄板面内的积分域。
从而得到求解S(t)的非线性常微分方程。
(49)
式中,ω0为相应线性问题用Galerkin法求得的固有频率;β为非线性参数;F(t)为外激励力。
(50a)

(50b)
(50c)
对于自由振动问题,式(49)可以改写为如下形式:
(51)
一般情况下,非线性参数β较小,可以用小参数项进行标记。
(52)
式中,E为小参数。
利用Lindstedt-Poincaré摄动法(Lindstedt-Poincaré Perturbation Method)进行求解。
(53)
式中,ωN为非线性振动频率;ω0为线性固有频率;bn为n次小参数项的系数。
式(51)的解可展开为E的多项式。
S(t)=s0(t)+Es1(t)+E2s2(t)+…+Ensn(t)
(54)
式中,sn为n次小参数项对应的位移,代表了不同的时间尺度。
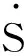
S(0)=s0(0)+Es1(0)+E2s2(0)+…=S0
(55a)

(55b)
将式(53)和式(54)代入式(52),式(52)的两端可分别表述为如下形式:
(56a)

比较式(56a)和(56b)两端E的同次幂系数,形成一系列线性常微分方程的初值问题。
(57a)
(57b)
(57c)
式中,T0为s0时间尺度下的位移初值。
依次对式(57)各式的初值进行求解。式(57a)表述的是一个线性无阻尼系统自由振动问题,其解析表现为如下形式:
(58)
式中,a0为位移幅值。
将式(58)代入式(57b),经过整理,可以得到关于s1的线性微分方程。
(59)

(60)
因此,式(59)的解可表述为如下形式:
(61)
将求得的s0和s1代入式(57c),经过与上面类似的求解及分析过程,可求出相关参数。
(62)
(63)
同样地,可以求取b3,b4,b5,…,以及s3,s4,s5,… ,等等。
将求出的系数b1,b2,b3,…,代入式(53),可得到
(64)
将s0,s1,s2,s3,…代入式(54),可得式(51)的解。
(65)
得到S(t)后,回代到式(47),即可得到等效非线性弹性板的非线性振动解。
5.1.3 边界条件
在等效非线性弹性板非线性运动方程的解[见式(47)]中,w0(x,y)为满足全部边界条件的挠度函数,可根据板的不同形状及边界条件确定。
对于悬臂薄板(见图48),其需满足的边界条件只有固支和自由等两种形式。

图48 悬臂薄板中面Fig.48 Cantilever thin plate mid-plane
(1)固支边 在x=0处,平板边界完全固定,其边缘上各点横向位移为零,且横向位移在截面位置坐标x=0处的斜率或横向位移对x的一阶导数为0。
(66)
(2)自由边 在x=a,y=0,y=b处,若平板边界完全不受力,则边缘上各点弯矩、扭矩、剪力为零。采用Kevin-Kirchhoof合力边界条件,可合并扭转和剪力。
(67)
5.1.4 固有特性求解
对于悬臂的等效非线性弹性板,可采用双向梁函数组合级数进行求解。
设板的挠度振型函数可以表示为如下形式:
(68)
式中,Amn为待定系数,用来调整不同阶次梁函数组合,以逼近板件振型真实解;Φm(x)为与x方向两端边界条件相对应的梁的第m阶振型函数;Ψn(y)为与y方向两端边界条件相对应的梁的第n阶振型函数。
(69a)
(69b)
coshλmacosλma+1=0,coshμnbcosμnb-1=0
(69c)

(69d)
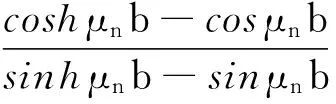
(69e)

(69f)
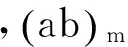

表18 不同边界条件单向板的频率系数Tab.18 Frequency coefficients of one-way plate under different boundary conditions
对于边界条件不以对角线为对称的板(包括方板、矩形板),以及边界条件以对角线为对称的矩形板(两邻边边长相差较大),其振型以Φm(x)Ψn(y)为主[85]。考虑到多项组合法解中均有一项为主的特点,对于梁函数组合法解上述边界条件板的振型,可以进一步简化,即可在式(69)中仅取单独一项。
(70)
式中,wmn(x,y)为简化的薄板振型函数。
将式(70)代入式(50a),可得
(71)
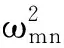
具体而言,根据式(65),非线性系统自由振动的一次近似解可表述为如下形式:
(72)
式中,ωN为固有频率。
(73)
等效非线性弹性板的振动解可表述为如下形式:
(74)
5.2 悬臂硬涂层-薄板固有特性分析算例
5.2.1 分析对象及其材料参数等效
以涂覆NiCrAlY和Mg-Al涂层材料的钛合金(Ti-6Al-4V)板(见图49)为例进行分析。

图49 硬涂层-薄板试件实物Fig.49 Hard coating-thin plate test piece schematic
钛合金板的几何尺寸以及涂层厚度见表19,涂层的材料参数见表20。

表19 薄板的尺寸及涂层厚度Tab.19 Dimensions and coating thickness of plates

表20 硬涂层材料参数Tab.20 Hard-coating material parameters
悬臂硬涂层-薄板的弹性模量E,剪切模量G和泊松比ν,可以用涂层材料与钛板的材料参数进行等效。

(75a)

(75b)
式中,EC为涂层的弹性模量;ES为基板的弹性模量;vC为涂层的体积分数;vS为基板的体积分数;νC为涂层的泊松比;νS为基板的泊松比。
计算得到的悬臂硬涂层-薄板的等效材料参数如下。
板ⅠC:E=119.68 GPa,G=45.91 GPa,ν=0.309 9;
板ⅡC:E=113.57 GPa,G=43.68 GPa,ν=0.309 9;
板ⅢC:E=113.57 GPa,G=43.68 GPa,ν=0.309 9。
对于非线性材料系数B,采用图形拟合方法来确定。图50中,直线ⅠL为硬涂层-薄板的线性弹性模量E,曲线ⅡL和曲线ⅢL分别为B取5 000和10 000时的非线性应力-应变关系曲线。可以看出,B取5 000时更符合物理非线性。
在获得所需的材料参数之后,运用Maple软件对有关算式进行编程和计算,求出硬涂层-薄板前5阶固有频率。

图50 硬涂层-薄板应力-应变曲线Fig.50 Stress-strain curves of hard-coating plate
5.2.2 有限元与实验验证方法
(1)有限元计算 依照所提供硬涂层-薄板的模型和材料,对硬涂层-薄板进行有限元建模。钛合金基板采用SOLID5实体单元,涂层选用SHELL181单元,边界条件设为悬臂,采用Block Lanczos方法进行模态分析。图51为建立的钛合金板ⅠC、ⅡC和涂层板ⅢC的模型。
可以通过各向同性材料的弹性模量E和泊松比ν得出材料的弹性常数C11和C12。经计算所得结果见表21,其余参数为测试所得。

图51 在ANSYS中建立的模型Fig.51 Models built in ANSYS

表21 硬涂层材料的弹性常数Tab.21 Elastic coefficients of hard-coating materials
(2)实验测试 将硬涂层-薄板装入夹具,夹紧使其处于悬臂状态(见图52)。首先使用锤击法初步获得硬涂层-薄板的固有频率,以此为参考,使用电磁振动台进行扫频激励,采集试件的响应信号,以精确获得硬涂层-薄板的固有频率。考虑到硬涂层具有软式非线性特征,扫频时采用从高频到低频的方式进行。扫频结束后,从等时间间隔的自功率谱组成的瀑布图中辨识出硬涂层-薄板的固有频率。

图52 悬臂硬涂层-薄板的固有频率测试Fig.52 Natural frequency test of cantilever hard-coating plate
5.2.3 结果对比与分析
Mg-Al合金涂层-薄板ⅠC、NiCrAlY涂层-薄板ⅡC和NiCrAlY涂层-薄板ⅢC的固有频率的线性解析解、非线性解析解以及有限元计算和实验测试的结果见表22、表23和表24。
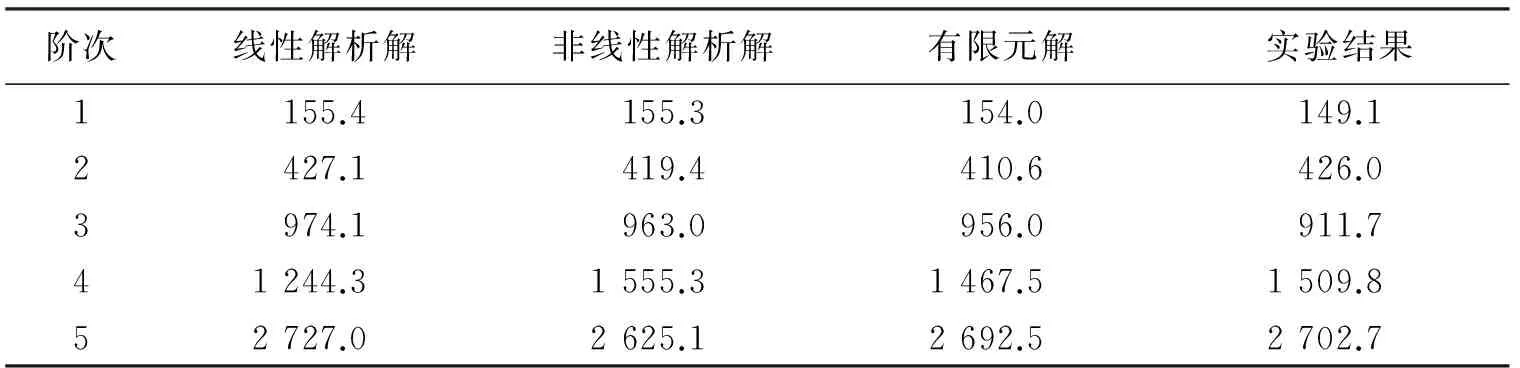
表22 Mg-Al合金涂层-薄板ⅠC的固有频率Tab.22 Natural frequencies of Mg-Al alloy coating plate ⅠC Unit:Hz

表23 NiCrAlY涂层-薄板ⅡC的固有频率Tab.23 Natural frequencies of NiCrAlY coating plate ⅡC Unit:Hz

表24 NiCrAlY涂层-薄板ⅢC的固有频率Tab.24 Natural frequencies of NiCrAlY coating plate ⅢC Unit:Hz
从表22~表24可以看出,近似解析方法求得的固有频率和有限元计算及实验测试所得的固有频率基本一致,差异非常小。
为了比较4种方法的准确程度,将其求解的固有频率进行了比较,结果见图53~图55。从图53可以看出,对于Mg-Al合金涂层-薄板,非线性解析方法和有限元方法所求得的固有频率以及实验测试的结果十分贴近,只有线性解析方法求得的固有频率在3阶以后相差的比较大。
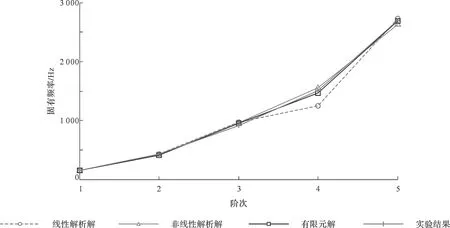
图53 Mg-Al合金涂层-薄板ⅠC的固有频率Fig.53 Natural frequencies of Mg-Al alloy coating plate ⅠC
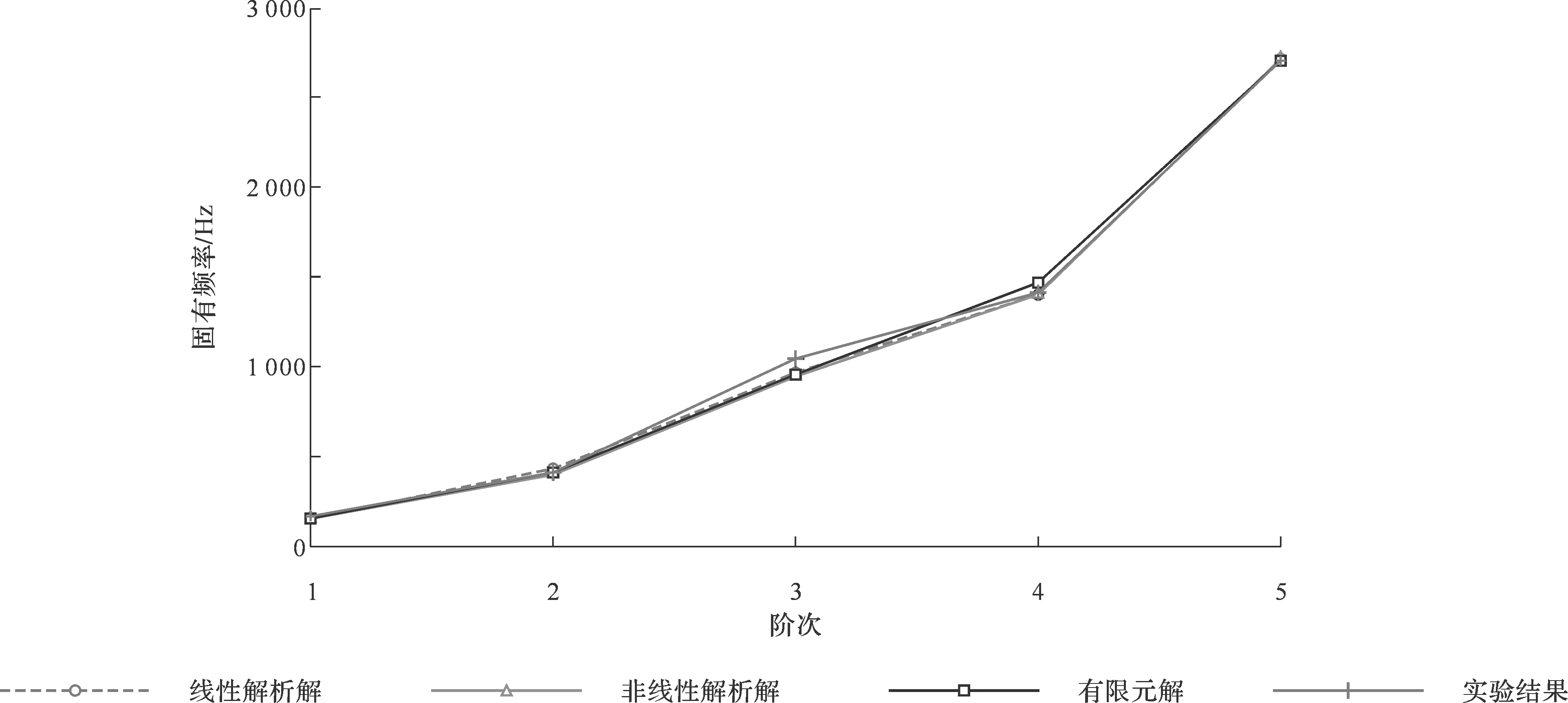
图54 NiCrAlY涂层-薄板ⅡC的固有频率Fig.54 Natural frequencies of NiCrAlY coating plate ⅡC
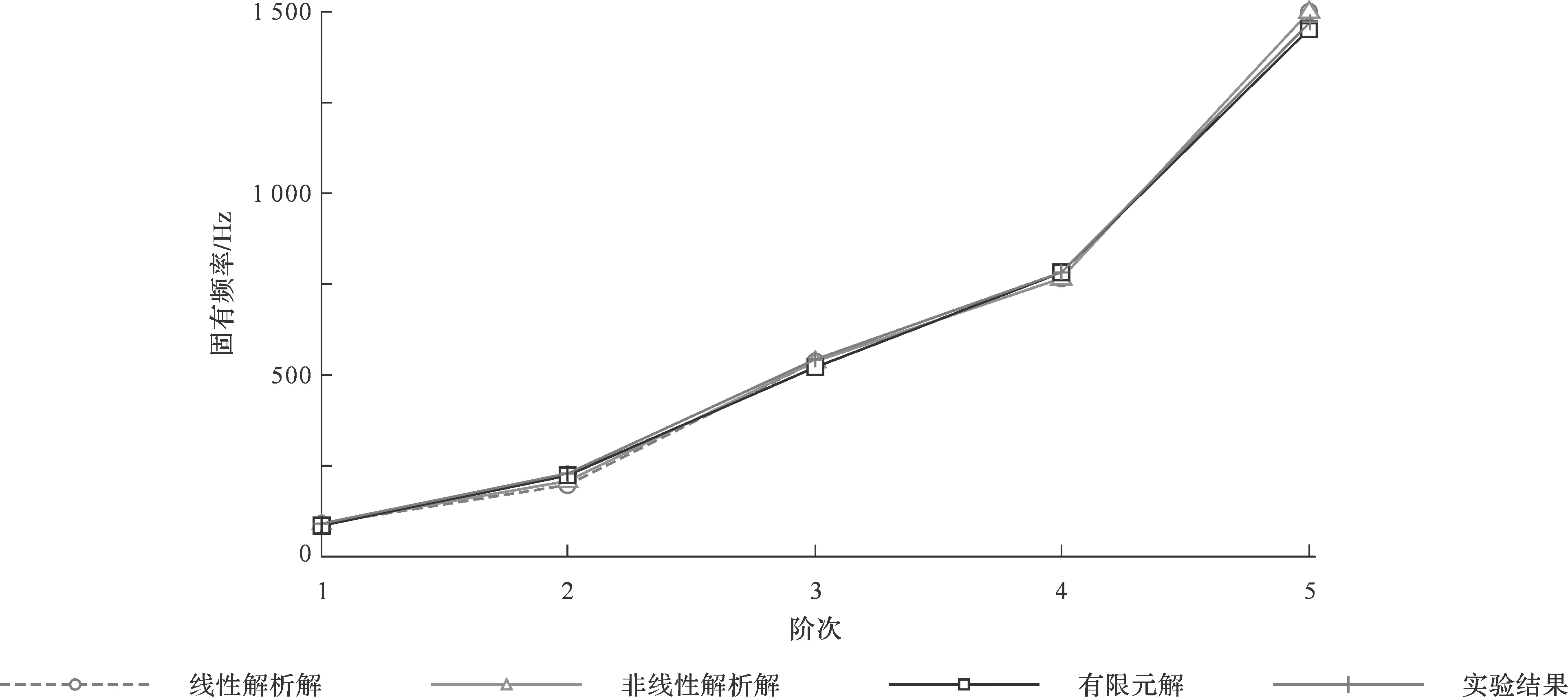
图55 NiCrAlY涂层-薄板ⅢC的固有频率Fig.55 Natural frequencies of NiCrAlY coating plate ⅢC
另外,从表25可以看出,近似解析计算的振型与有限元振型,以及实验测试所得的振型是一致的。

表25 硬涂层-薄板的振型Tab.25 Vibration modes figures of hard-coating plate
[注]m为长度方向上的半波数,n为宽度方向上的半波数。
6 硬涂层-薄板的非线性振动
横向载荷作用的悬臂硬涂层-薄板非线性振动响应可表述为如下步骤。
【step1】 基于von Karman理论(von Karman Thoery)和Reddy三阶剪切变形板理论(Reddy Third Order Shear Deformation Theory of Plate,RTOSDTP),采用Hamilton变分原理建立硬涂层-薄板非线性动力学方程(Nonlinear Dynamic Equations of the Hard-Coating Thin Plate,NDEHCTP);
【step2】 利用Galerkin离散法(Galerkin Discrete Calculation Method)对NDEHCTP进行离散,得到硬涂层-薄板横向变形非线性控制方程(Nonlinear Governing Equation of the Lateral Deformation,NGELD);
【step3】 对在横向谐波(horizontal harmonic wave)基础激励作用下的悬臂矩形钛合金薄板和悬臂硬涂层-薄板非线性振动响应进行测试分析。
6.1 硬涂层-薄板的非线性运动控制方程
对于硬涂层-薄板(见图56),作出如下规定。
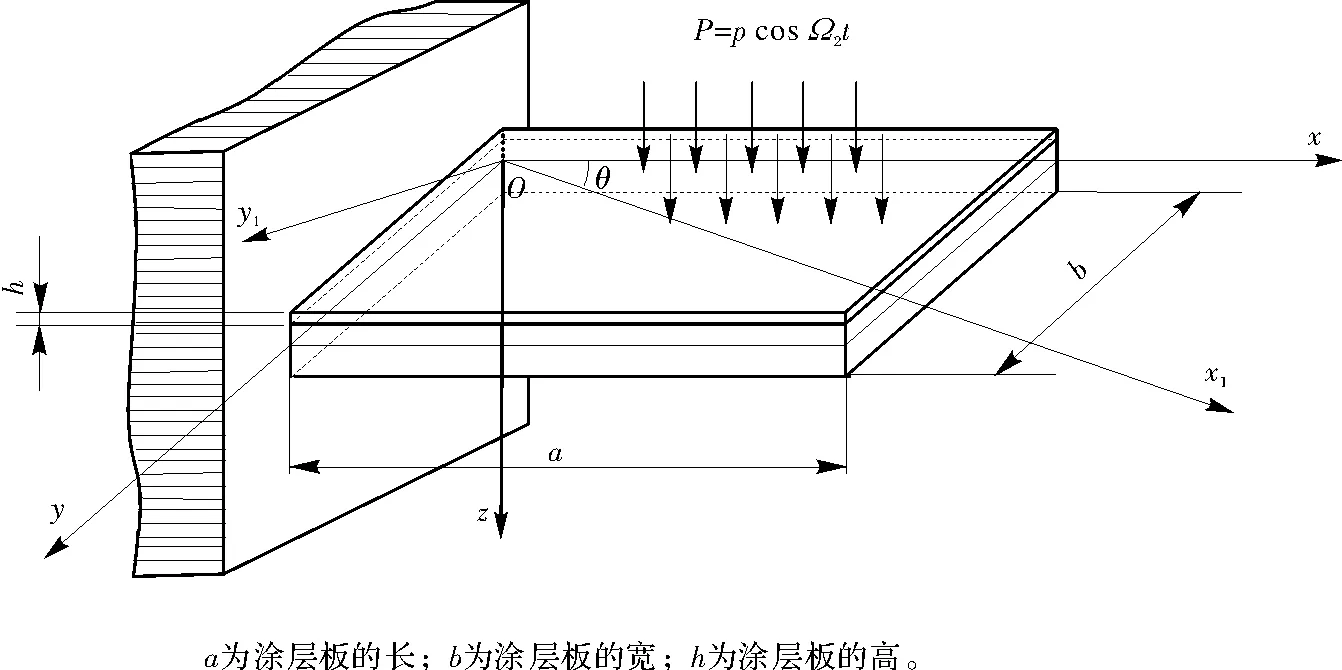
图56 横向载荷作用下的悬臂硬涂层-薄板模型Fig.56 Cantilever hard-coating thin plate model suffering transversal excitation
【规定1】 硬涂层材料为各向异性材料,基体为线弹性材料。
【规定2】 直角坐标oxy位于层合板的中性面内,z轴向下。
【规定3】 根部受到约束,即为悬臂状态。
【规定4】 假设受到的外载荷为横向载荷,即垂直于oxy面并沿z方向(见图56中的P)。
根据复合材料结构Voigt-Reuss预估方法,按照式(75)等效处理硬涂层-薄板材料参数。
根据Reddy三阶剪切变形板理论(RTOSDTP),板的位移场可以表述为如下形式。
(76a)
(76b)
(76c)
式中,u为板内任一点沿x方向的位移;v为板内任一点沿y方向的位移;w为板内任一点沿z方向的位移;u0,v0和w0为硬涂层-薄板的中面任一点沿x,y和z方向上的位移;φx为板变形后的中面法线对x的转角;φy为板变形后的中面法线对y轴的转角。
若硬涂层-薄板的应变-位移关系(几何关系)为非线性关系,则可以表述为如下形式。
(77a)

(77b)
式中,εxx为x方向正应变;εyy为y方向正应变;γxy为xy面内的剪切应变;γyz为yz面内的剪切应变;γxz为xz面内的剪切应变。
根据Hamilton原理,可以得到系统的动力学方程。
(78a)
(78b)
(78c)
(78d)
(78e)
(78f)
(78g)
(78h)
(78i)
(78j)
(78k)
c1=4h2/3,c2=2c1
(78l)
式中,γ为横向振动阻尼系数;p为外载荷的幅值;Ω2为外载荷的频率;Nxx,x为Nxx对x求偏导;Pxy,xy为Pxy依次对x,y求偏导;其余依次类推。
将式(78a)和式(78b)代入式(78c),可以得到如下形式:
(79)
这样,可以得到由w0,φx和φy表示的硬涂层-薄板非线性动力学方程。
(80a)
(80b)
(80c)
(81a)
(81b)
(81c)

(81d)
由于板是关于中面对称的,根据奇函数性质,可以得到以下形式。
Bij=0,Eij=0,I1=0,I3=0,J1=0
(82)
通过Hamilton原理所得到的式(80)为偏微分形式,为方便分析,可使用Galerkin方法将其离散为常微分方程组。
对于横向面外载荷作用下一边固支、三边自由的硬涂层-薄板,横向非线性振动是其主要振动形式,且远大于其面内振动,许多学者对悬臂板进行研究时只考虑其横向振动位移[86]。本文也采取这种处理方法,对横向非线性振动位移(Lateral Nonlinear Vibration Displacement)进行二阶离散。
由悬臂板的边界条件出发,其模态函数可以表述为如下形式:

(83a)

(83b)

(83c)

(83d)

(83e)
式中,u1,v1,w1分别为第1阶模态x,y,z方向的位移;φ1,φ3分别为第1阶模态变形后的板中面法线对x和y轴的转角;u2,v2,w2为第2阶模态x,y,z方向的位移;φ2,φ4分别为第2阶模态变形后的板中面法线对x和y轴的转角。
把式(83)带入无量纲化后的式(80),并在“=”两边分别乘以对应的模态函数,在整个板积分,利用三角函数的正交性,得到两自由度非线性动力学方程。
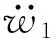
(84a)
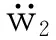
(84b)

6.2 基于实验测试的硬涂层-薄板非线性振动分析
6.2.1 实验设备
以151.9 mm×110 mm×1.5 mm的钛合金板ⅢC和带有NiCrAlY硬涂层的薄板为实验对象,夹持后的悬臂板尺寸为122 mm×110 mm×1.5 mm(见图57)。

图57 钛合金板ⅢC硬涂层-薄板实物Fig.57 Photo of titanium alloy plate ⅢC and hard-coating thin plate
在固有特性、振动响应及阻尼比的测试中,实验设备的选用见表26。针对振动响应测试,实验组配的测试系统见图58。

表26 测试内容及选用仪器Tab.26 Test items and chosen apparatus

图58 悬臂钛合金板振动测试系统Fig.58 The vibration measurement system of cantilever Titanium alloy plate
6.2.2 测试步骤
【step1】 根据有限元分析计算结果呈现的钛合金板各阶模态振型特点,分析各阶振型所对应的节点和节线分布,建立实验测点构成的线框模型(见图59);
【step2】 采用锤击法获得悬臂钛合金板的各阶固有频率值;
【step3】 变换敲击点,获取悬臂钛合金板的模态振型;
【step4】 以1g激振力幅,选取锤击法获得的各阶固有频率的75%~125%作为扫描频段,在此频段内以0.2 Hz/s或者更低的速度进行扫频测试,使用轻质加速度传感器获取响应信号;
【step5】 获得由等时间间隔的功率谱组成的三维瀑布图(见图60),从瀑布图准确辨识1g幅值扫频激励下悬臂钛合金板的固有频率;
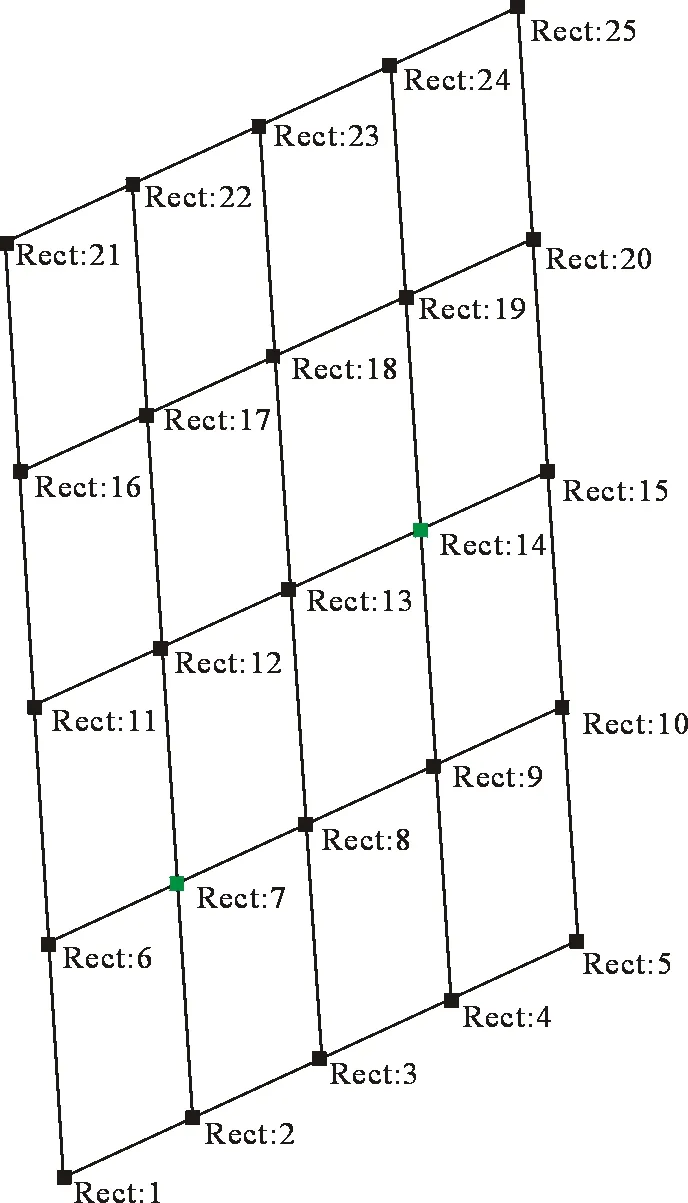
图59 钛合金板线框模型Fig.59 Wireframe model of titanium alloy plate

图60 扫频三维瀑布图Fig.60 3D Waterfall when sweeping
【step6】 以各阶固有频率作为激振频率对悬臂钛合金板进行激振,待达到稳定后停止激励让其自由振动直至衰减到静止,从衰减信号中辨识悬臂钛合金板的各阶模态阻尼比(见表27);
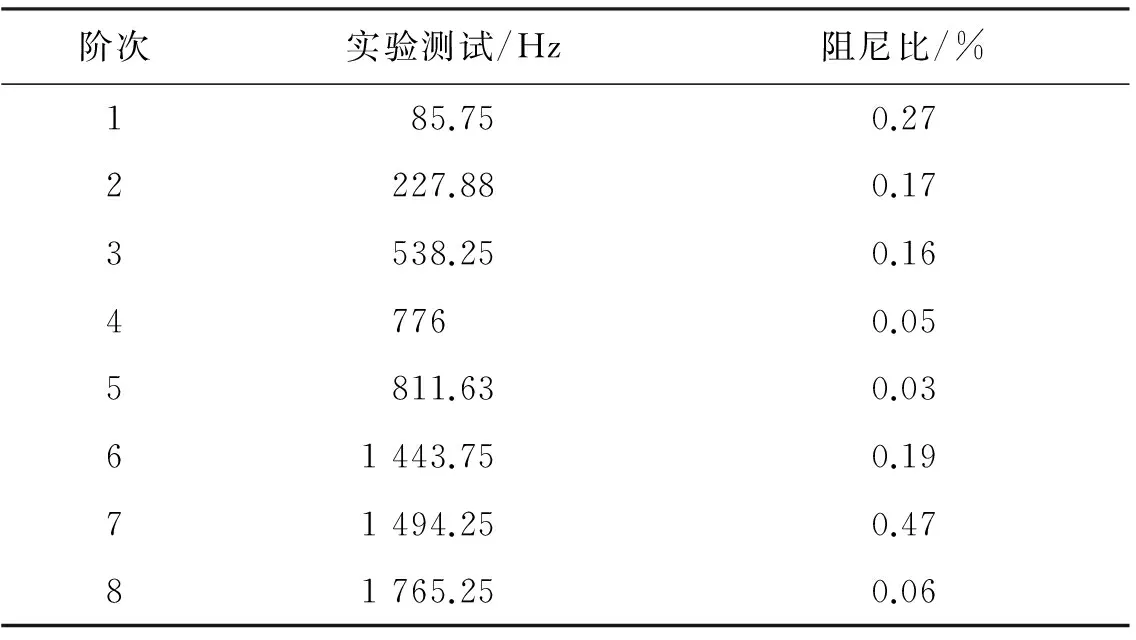
表27 钛合金板的前8阶固有频率及阻尼比Tab.27 Natural frequencies and damping ratio of titanium alloy plate
【step7】 在钛合金板ⅢC上使用物理气相沉积(PVD),涂敷NiCrAlY涂层20 μm,通过上述测试步骤得到涂层板的固有频率和阻尼比(见表28)。
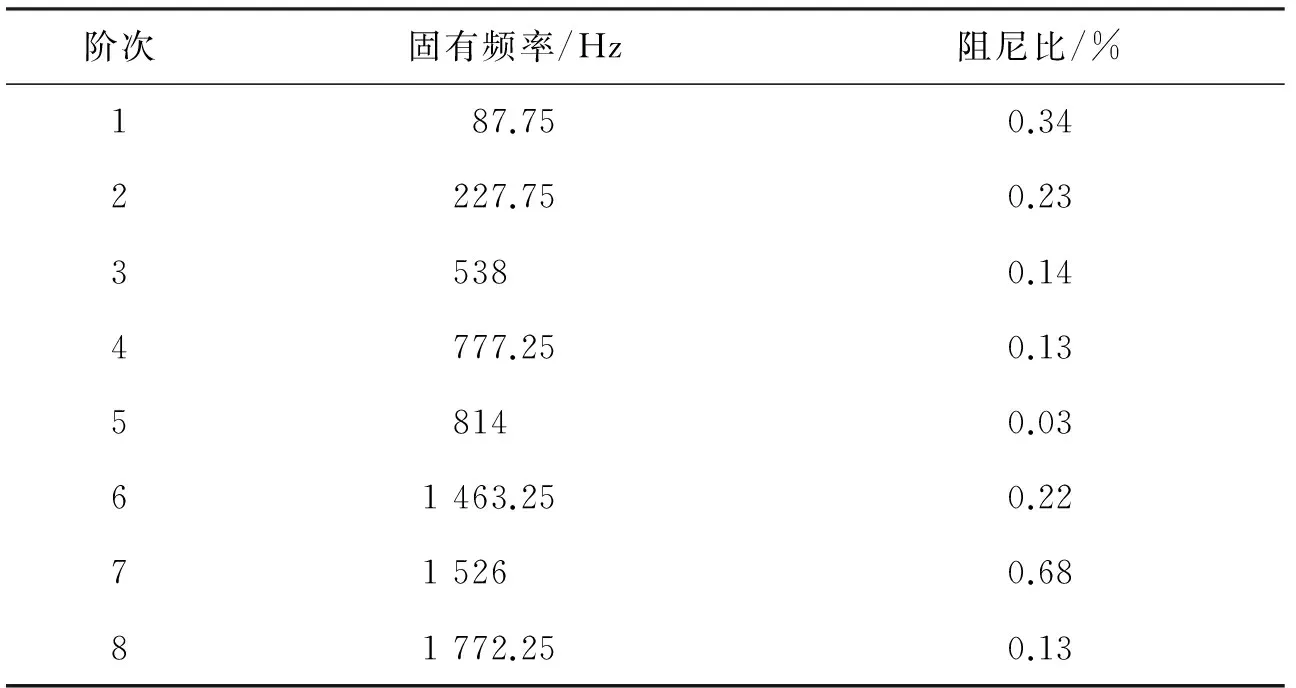
表28 硬涂层-薄板的前8阶固有频率及阻尼比Tab.28 Natural frequencies and damping ratio of hard-coating thin plate
6.2.3 激振频率对振动行为的影响
响应测试旨在研究1g激振力幅下,激振频率Ω的变化对板的振动行为的影响。使用振动台以0.4 Hz/s的速率在30~2 200 Hz之间进行连续扫频振动,实时观测悬臂板的响应信号特征,判断板具体的振动行为;根据振动行为的不同划分出不同的频率段;对钛合金板涂层前后的振动行为进行对比。
(1)钛合金板的振动响应特征 根据实时观测到的悬臂钛合金板不同激振频率Ω下的动响应特征,可以划分成如下频率段。
①当Ω为30~190 Hz时,板的振动响应表现多周期运动,此时的功率谱不仅包含有激振频率的成分,而且还出现了6阶和7阶固有频率[见图61(a)和图61(b)]。
②当Ω为210~439 Hz时,板的响应表现为四倍周期运动,功率谱除了包含有激振频率的成分外,还出现了3阶、6阶和7阶固有频率[见图61(c)]。
③当Ω为459~519 Hz时,板的响应表现为与激振力同频的简谐运动-单倍周期运动,其运动波形和正弦曲线的形状相类似,其功率谱以激振频率为其基本频率成分[见图61(d)]。
④当Ω为620~760 Hz时,板的响应表现为混沌运动,其功率谱为连续谱[见图61(e)和图61(f)]。
⑤当Ω为770~790 Hz时,板的响应表现为二倍周期运动,功率谱的成分为激振频率和激振频率的2倍频率。由于在这一区间的频率约为第7阶固有频率的1/2,所以认为这一区间的频率引发了板的1∶2内共振[见图61(g)]。
⑥当Ω继续增大,板的响应经历混沌运动[Ω=791~1 099 Hz,见图61(h)]→多周期运动[Ω=1 100~1 348 Hz,见图61(i)]→单倍周期运动[Ω=1 349~1 860 Hz,见图61(j)]→混沌运动[Ω=1 870~2 200 Hz,见图61(k)]。


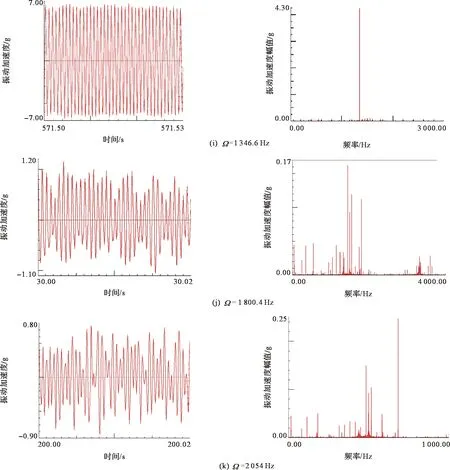
图61 各激振频率下悬臂涂层钛板的振动行为Fig.61 Vibration characteristics of the cantilevered hard-coating Titanium plate under different excitation frequencies
(2)硬涂层-薄板的振动响应特征 根据实时观测到的不同激振频率Ω下悬臂硬涂层-薄板的振动响应特征,可以划分成以下频率段。
①当Ω为30~175 Hz时,板的响应表现多周期运动,功率谱不仅包含有激振频率的成分,还出现了3阶、6阶和7阶固有频率[见图62(a)和图62(b)]。
②当Ω为140~440 Hz时,板的响应表现为四倍周期运动和三倍周期运动交替出现[见图62(c)和图62(d)]。
③当Ω为450~600 Hz时,板的响应表现为与激振力同频的简谐运动-周期运动,其运动波形和正弦曲线的形状类似,其功率谱以激振频率为基本频率成分[见图62(e)]。
④当Ω为600~716 Hz时,板的响应表现为混沌运动,功率谱表现为连续谱[见图62(f)]。
⑤当Ω为720~1 110 Hz时,板的响应表现为多周期和混沌运动交替出现[见图61(g)、图62(h)和图62(i)]。
⑥当Ω为1 110~1 718 Hz时,板的响应表现为周期运动[见图62(j)和图62(k)]。
⑦当Ω为1 806~2 200 Hz时,板的响应表现为准周期运动[见图62(l)和62(m)]。


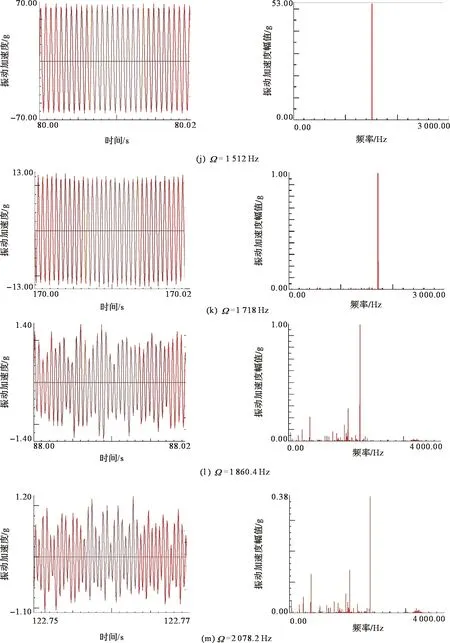
图62 硬涂层-薄板的振动行为Fig.62 Vibration behaviours of hard-coating thin plate
比较图61和图62,可以发现,硬涂层-薄板比钛合金薄板的振动行为要复杂,但是发生混沌运动的区间比钛合金薄板小,尤其是在高频率范围,硬涂层抑制了混沌运动的发生。
6.2.4 各阶共振区的振动响应特性
为了研究钛合金薄板涂层前后的稳态主共振幅频响应的变化规律,对钛合金板涂层前后的振动行为进行了研究和对比分析。
在各阶固有频率附近,以0.2 Hz/s的速率(保证薄板的振动为稳态)进行精细扫频,采集到其时域信号后进行FFT,观察各阶共振区的幅频响应。考虑到硬涂层的软式非线性特点,扫频时采用从高到低的方式。
图63为得到的前8阶固有频率附近的幅频响应曲线。



图63 稳态主共振的幅频响应比较Fig.63 Amplitude-frequency response comparison of steady-state primary resonance
当激振频率Ω=84.5 Hz时(一弯),实验中观察到钛合金板的1阶共振突然停止,几秒后又突然开始,并比开始时剧烈。通过观察幅频曲线发现产生了跳跃现象[见图63(a1)]。
分析悬臂钛合金薄板和悬臂硬涂层-薄板的主共振的响应,响应的幅频曲线见图63,硬涂层-薄板响应的振幅明显小于钛合金薄板。比较共振区钛合金薄板和硬涂层-薄板的实测幅频响应振幅,1~5阶的振幅都比较相近,第5阶以及更高阶次的钛合金薄板的振幅是硬涂层-薄板的3~15倍这个结论与振动形态的差异相吻合,都证明了硬涂层优秀的减振效果。
7 硬涂层-薄板的阻尼优化设计
针对采用硬涂层对薄板结构进行阻尼减振的需求,采用优化设计,合理确定硬涂层的力学参数(弹性模量、损耗因子)和几何参数(涂敷厚度等),可有效地实现硬涂层阻尼减振。硬涂层-薄板阻尼优化设计步骤如下。
【step1】 建立硬涂层-薄板力学特性表征规则,定义基于Reuss模型的复合结构力学特性计算模型(Mathematical Model of Composite Structures Based on Reuss Model,MMCSBRM)。
【step2】 定义硬涂层-薄板阻尼优化设计的目标函数和约束条件,建立基于Reuss模型的优化设计流程(Optimizational Design Process Based on the Reuss Model,ODPBRM)。
【step3】 以钛合金薄板为实例,采用ODPBRM对硬涂层的弹性模量、损耗因子,以及涂敷厚度进行寻优,评判其对于硬涂层-薄板结构系统力学特性的贡献。
【step4】 利用有限元法,采用优化设计得到的涂层力学特性参数及几何参数,求解涂敷硬涂层前后薄板结构的固有特性、模态阻尼比和谐响应,对优化设计得到的参数进行硬涂层阻尼减振效果的对比验证。
7.1 硬涂层-薄板结构力学特性表征及计算模型
7.1.1 硬涂层-薄板结构力学特性的表征
硬涂层-薄板结构由硬涂层和基体等两部分组成(见图64)。

图64 涂层阻尼复合结构Fig.64 The coating damp of composite structure
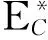
(85a)
(85b)

ηC和ηS可以表达为如下形式:

(86a)

(86b)
式中,δC为涂层应力-应变的相位差角;δS为基体涂层应力-应变的相位差角。
硬涂层-薄板的力学特性可以用复模量E*来表征,其具体数值由硬涂层和基体的复模量、厚度等因素综合确定。
E*=E′+iE″=E′(1+iη)
(87)
式中,E′为薄板复合结构的储能弹性模量;E″为薄板复合结构的耗能弹性模量;η为复合结构的损耗因子。
为了便于设计与分析,规定硬涂层-薄板的力学特性用复模量E*的模,及其结构的损耗因子来描述。
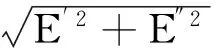
(88a)
η=tanδ
(88b)
式中,E为复模量E*的模;η为复合结构的损耗因子;δ为复合结构应力-应变的相位差角。
7.1.2 硬涂层-薄板结构力学特性计算模型
Reuss公式被广泛用于预测层合复合材料和结构的力学特性。按照图64,硬涂层-薄板非常接近Reuss复合结构。
(89a)
∑Vi=1
(89b)
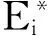
对于涂层结构,假设涂层整体覆盖基体,Reuss公式可以简化为如下形式:
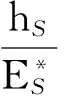
(90a)
hC+hS=1
(90b)
式中,hS为基体所占份额;hC为涂层厚度所占份额。
若将式(87)代入式(90),分离E*的实部及虚部,将可以获得涂层复合结构系统模量E和损耗因子tanδ[87]。
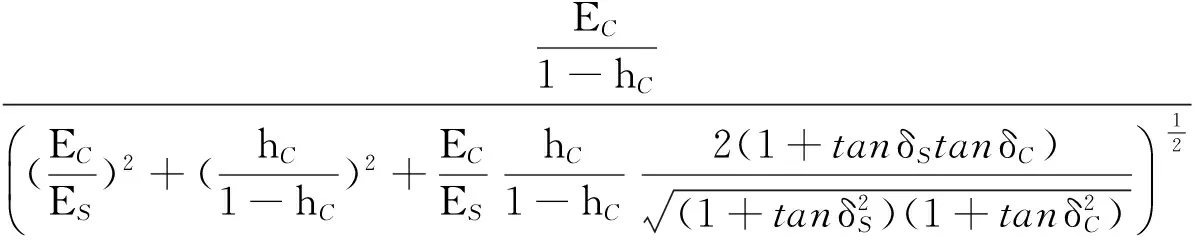
(91)

(92)
7.2 硬涂层-薄板结构的阻尼优化设计方法
7.2.1 优化设计目标函数
Lakes[87]提出了如下形式的涂层复合结构系统阻尼近似计算模型:

(93)
式(93)表明,涂层系统总的损耗因子与涂层及基体的储能弹性模量、厚度、涂层的损耗因子相关。如若仅追求复合结构损耗因子最大化,只要相应地增加涂层的厚度。实际应用上,无限制地增大涂层厚度并不可行,这是因为涂层增厚容易出现涂层剥落,而且结构限制也不允许涂层过厚。
涂层阻尼减振终极目的是降低振动的响应幅度,进而提高结构的综合强度和服役寿命。Brodt[88]提出将Etanδ作为考核复合结构系统性能的指标。如果Etanδ大,表明复合结构性能优越。对于常用金属结构材料,Etanδ<0.6GPa[18],而通过优化选取涂层材料的性能参数,可使复合材料结构的组合性能大于此值。对于硬涂层-薄板结构阻尼优化设计,本文以Etanδ最大化为设计目标。目标函数可以表示为如下形式。
minf(X)=-Etanδ
(94)
式中,X为设计变量。
参照式(88)和式(89)求解E和tanδ,可以构建薄板结构阻尼优化设计的目标函数。
7.2.2 硬涂层阻尼减振设计约束条件
硬涂层-薄板结构阻尼减振设计,通常是针对特定的金属基体,寻求具有最佳力学性能参数、厚度参数的硬涂层材料。
对于本文的优化设计问题,规定金属基体的材料特性参数和厚度为常值。对应于式(95),设计变量包括硬涂层的厚度,弹性模量和损耗因子ηC。
【硬涂层阻尼减振设计原则】 不破坏原结构功能特性,涂层厚度不能过大。
根据硬涂层阻尼减振设计原则,对于薄板结构,涂层厚度(以μm为单位)占总厚度的百分比必须达到如下要求:
×100%<10%
(95)
式中,hC为硬涂层厚度;hS为基体厚度。
从化学成分来讲,硬涂层材料主要是阻尼合金、陶瓷材料,以及两者的混合体,其弹性模量及损耗因子与单一结构材料相比有很大不同。
硬涂层的弹性模量受制备过程影响较大。以等离子喷涂为例,涂层弹性模量受给料颗粒的尺寸、物相组成、喷涂过程和后处理等众多因素的影响。因而,硬涂层的弹性模量EC有较大的取值范围。
硬涂层材料的内阻尼不如有机粘弹性阻尼材料高,但远大于铁、铝等金属材料[89]。对于有机粘弹性材料,其损耗因子通常大于0.1;对于普通金属,损耗因子通常小于0.01。由此,可以大致确定硬涂层材料损耗因子的约束条件。
考虑到结构自身性能的约束以及工艺条件,涂层厚度hC的变动范围为0.01%~10%;考虑到单一的陶瓷虽然能满足硬度要求但易碎,因此取陶瓷与金属的混合体作为涂层材料,弹性模量EC的变动范围为1~200 GPa;考虑到硬涂层的损耗因子比普通金属大,而比聚合物弹性阻尼材料小,损耗因子ηC(ηC=tanδC)的变动范围为0.001~0.1,故而约束条件可表达为如下形式:
(96)
式中,EC为弹性模量。
由式(96)可见,硬涂层材料的机械特性参数取值范围较大,这给硬涂层减振优化设计提供了较大的选择空间。
【硬涂层涂敷原则】 不降低基体结构的强度。
通常期望涂层复合结构的弹性模量值E大于基体的弹性模量ES。但有些情况下,涂敷硬涂层后,会出现E (97) 7.2.3 寻优方法及优化设计流程 硬涂层-薄板结构优化设计为有约束优化设计问题,相关优化设计理论提供了多种方法(例如,随机方向法、可行方向法、复合形法、罚函数法,等等)可以用于求解该问题。 若该优化问题的设计变量可以表述为如下形式: (98) 则优化设计规则可表达为如下形式: (99) 若采用随机方向法(Method of Random Direction)进行求解,求解流程可概括为如下形式: 【step1】 选择一个满足约束条件[式(93)]的可行初始点X(0)。 【step2】 产生k个n维随机单位向量,这里n=3,k>n,随机向量的产生方法可参照下式。 (100) 【step 3】 计算出k个随机点X(j)(j=1,2,…,k)。 X(j)=X(0)+α0e(j)(j=1,2,…,k) (101) 式中,α0为试验步长。 【step 4】 在所产生随机点中,找出最佳随机点XL,产生可行的搜索方向S=XL-X(0),XL应满足约束条件,而且具有如下形式: (102) 【step 5】 从初始点X(0)出发,沿可行搜索方向S以加速步长α=cα0进行迭代计算,直到搜索到一个满足全部约束条件, 且目标函数值不再下降的新点X。 【step 6】 检验是否满足收敛条件。 (103) 若满足式(103),迭代终止,最优解为X*=X,f(X*)=f(X);若不满足式(103),令X(0)←X,转到step 2,重新搜索。 7.3 阻尼优化实例 7.3.1 钛合金薄板设计参数优化 【step1】 取钛合金(Ti-6Al-4V)薄板进行硬涂层减振设计参数优化。 Ti-6Al-4V力学性能参数[4]如下。 ES=1.103 2×1011Pa,νS= 0.31,ρS=4 420 kg/m3,tanδS=0.000 7 (104) 【step2】 按照优化设计流程,优化确定涂层厚度、涂层材料弹性模量、损耗因子等设计参数。 设起始点参数值如下。 (105) 将初始值代入到式(88),可得涂层钛合金薄板弹性模量E=1.06×1011Pa,E 采用Matlab.进行编程运算,获得最优值。 (106) 根据选定的最优设计参数,钛合金薄板涂层前后力学性能对比见表29。 表29 涂敷前后钛合金薄板力学特性的变化Tab.29 Mechanical character difference between the bare and titanium-substrate coated thin plate 对比上述数据,可以看到,通过涂敷选定参数的硬涂层材料,钛基薄板的损耗因子tanδ及组合性能指标Etanδ分别提高了26.7倍和24.2倍,而复合结构的总体弹性模量降低,降幅为12.75%。 需要特别指出的是,硬涂层材料的力学特性参数与涂敷工艺、颗粒大小等直接相关,具有很大的不确定性,优化流程确定的涂层最优设计参数只能作为选择和制备硬涂层材料的参考;实际的硬涂层材料,其性能还需要通过实验进行测试。 7.3.2 涂层设计参数对硬涂层薄板复合结构力学性能的贡献 为了进行硬涂层阻尼减振设计,需要明确涂层弹性模量、损耗因子和涂层厚度等参数对硬涂层薄板复合结构力学性能的贡献规模。 7.3.2.1 涂层弹性模量 取涂层的厚度、损耗因子为优化设计所确定的最优值,考核涂层弹性模量EC对于薄板复合结构组合性能指标Etanδ、减振能力指标tanδ和薄板强度指标E的贡献。图65为基于Reuss模型绘制的涂层弹性模量贡献曲线,黑点为最优值。 图65 涂层弹性模量对薄板复合结构力学性能参数的贡献Fig.65 Contribution of elastic modulus of hard coating to mechanical property parameters of composite structure of thin plate 由图65可以得出如下结果。 【结果之一】 当涂层的弹性模量小于钛合金的弹性模量(EC 【结果之二】 当涂层弹性模量等于12.4 GPa时,组合性能指标Etanδ存在最大值,其值为3.08 GPa[见图65(a)],但是此时薄板复合结构的弹性模量E<60 GPa[见图65(c)],下降幅度超过了10%,不满足约束条件。 【结果之三】 薄板复合结构的损耗因子tanδ随着涂层弹性模量EC值的减少而增加[见图65(b)],约为<60 GPa以后,损耗因子tanδ增幅明显,表明涂层弹性模量小对于提高薄板复合结构的减振能力是有利的,但受薄板复合结构的强度所约束,涂层的弹性模量值不能太小。 【结果之四】 薄板复合结构的弹性模量E随着涂层弹性模量EC值的减少而减小,大约在<60 GPa以后,复合结构的弹性模量降幅明显。 7.3.2.2 涂层损耗因子 取涂层的弹性模量、厚度为优化设计所确定的最优值,考核涂层损耗因子tanδC对薄板复合结构组合性能指标Etanδ、减振能力指标tanδ和强度指标E的贡献。图66为基于Reuss模型绘制的涂层损耗因子贡献曲线,黑点为最优值。 从图66可以得出如下结果。 【结果之五】 涂层损耗因子tanδC越大,越有助于提高组合性能指标Etanδ及减振能力指标tanδ,而且增长的幅度可近似为一种线性关系[见图66(a)和图66(b)],因而在涂层材料选取时应该尽量选择具有大阻尼特性的材料。 图66 涂层损耗因子对薄板复合结构力学性能参数的贡献Fig.66 Contribution of dissipation factor of hard coating to mechanical property parameters of composite structure of thin plate 【结果之六】 涂层损耗因子tanδC对薄板复合结构的强度指标E的贡献很小,随着涂层的损耗因子从0.001增长到0.1时,薄板复合结构的强度指标E仅从99.21增为99.29[见图66(c)],可视为没有改变。因而,可以得出涂层损耗因子tanδC对薄板复合结构的强度指标E几乎没有影响的结论。 7.3.2.3 涂层厚度 取涂层的弹性模量、损耗因子为优化设计所确定的最优值,考核涂层厚度hC对薄板复合结构组合性能指标Etanδ、减振能力指标tanδ和强度指标E的贡献。图67为基于Reuss模型绘制涂层厚度的贡献曲线,黑点为最优值。 图67 涂层厚度对薄板复合结构力学性能参数的影响Fig.67 Contribution of coating thickness of hard coating to mechanical property parameters of composite structure of thin plate 从图67可以得出如下结果。 【结果之七】 薄板复合结构的组合性能指标Etanδ、减振能力指标tanδ,都是随着涂层厚度hC的增加而增加,而且增长的幅度可近似为一种线性关系[见图67(a)和图67(b)]。可见,涂层涂的越厚对于提升结构的组合性能和减振能力是有利的,但是受结构功能的限制,涂层又不能过厚,而且过厚的涂层容易剥落,从而影响减振效果。 【结果之八】 在涂层弹性模量为52.05 GPa的状态下,随着涂层厚度的增加,薄板复合结构的弹性模量明显降低,降幅也呈现出一种线性关系[见图67(c)],这也进一步说明在减振设计时涂层不能过厚。 7.4 硬涂层薄板结构阻尼优化减振效果验证 硬涂层阻尼减振效果需要进行有效地验证。这种验证,在方案设计阶段,主要基于理论分析或数值模型实施;对于施工完成后的涂层结构,主要以实验验证为主。 通过对比分析涂敷涂层前后的钛合金薄板,可以验证以下问题。 (1)固有频率有无偏移现象; (2)涂层后的复合结构振动响应有无降低; (3)涂层后的复合结构阻尼有无增加。 在此,拟采用有限元法检验涂层设计参数对钛合金薄板的减振效果。 7.4.1 计算条件与有限元模型 取110 mm×110 mm×3 mm的钛合金薄板。若薄板的一面被全部涂敷硬涂层材料,涂层的弹性模量、损耗因子和厚度为优化设计所确定的参数值,按照优化获得涂层厚度百分比,涂层厚度近似为3×10%=300 μm,参照相关硬涂层测试结果[4],假定涂层泊松比νC=0.3,涂层密度ρC=3.3×103kg/m3 用ANSYS软件进行分析,选择Solid95单元创建钛基体模型,Shell181单元创建涂层模型。Solid95是高阶的3D固体单元,有20个节点,每个节点有3个自由度。Shell181是中等厚度的壳单元,有4节点单元,每个节点有6个自由度。 以悬臂边界状态为例,创建涂层钛基薄板有限元模型(见图68),共 4 725个节点,800个实体单元,400个壳单元。 图68 涂层钛基薄板有限元模型Fig.68 Finite element analysis model of thin plate with titanium coating 7.4.2 固有频率与振型的对比 对涂敷硬涂层材料前后的钛合金薄板分别进行模态分析,采用分块兰索斯法(Lanczos),求取前9阶固有频率(见表30)。 表30 涂层前后钛基薄板固有频率Tab.30 The change of natural frequency of thin plate after titanium coating Unit /Hz 从表30可以看出,当涂敷硬涂层后,钛合金薄板的各阶固有频率值有所增加,发生了固有频率偏移现象,而且随着阶数的增加,固有频率差值越来越大。图69为对应的钛合金薄板前9阶模态振型,经过对比验证,发现在涂敷硬涂层后,钛合金薄板前9阶模态振型基本没有变化。 图69 钛合金薄板的前9阶模态振型Fig.69 The nine orders of modal shape of thin plate with hard coating 7.4.3 模态阻尼比的对比 假设待分析的系统中仅有材料阻尼耗能,分别求取涂层前后钛合金薄板的模态阻尼比。在ANSYS中用MP,DAMP命令定义材料阻尼。设定材料阻尼后,可采用无阻尼模态分析方法(例如Lanczos法)求解固有频率,进一步在后处理中利用*GET, , mode, ,DAMP命令来提取模态阻尼比。表31为涂层前后,钛基薄板的前9阶模态阻尼比。 表31 涂层前后钛基薄板模态阻尼比Tab.31 Difference of modal damping ratio of thin plate with titanium coating 从分析结果可以看出,涂敷硬涂层后,对应于各阶的模态阻尼比显著提高,总体上比未涂层结构大两个数量级,阻尼比的增大意味着薄板抗振能力的增强。 7.4.4 谐响应的对比 假设激励点与拾振点均在薄板的左下部(见图70)。设定激振力幅为100 N,同样假定仅有材料阻尼耗能,用ANSYS的模态叠加法进行谐响应分析。对比涂层前后薄板y方向响应的变化情况(见图71)。 从图71可以看出,钛板涂敷硬涂层阻尼材料后,对应共振峰的响应幅度明显下降,说明硬涂层阻尼材料具有明显的减振作用。钛合金薄板涂层前后,对应于各阶共振频率的谐响应峰值以及两者的对比见表32。 图70 谐响应激振力与拾振点的布置Fig.70 Location of knock and measurement points with resonance response 图71 涂层前后钛合金薄板谐响应对比Fig.71 Resonance response difference between the bare and coated titanium-substrate thin plate 表32 涂层前后钛合金薄板谐响应峰值的对比Tab.32 Resonance peak difference between the bare and coated titanium-substrate thin plate 8.1 结论 针对硬涂层-薄板结构的阻尼特性、固有特性与复杂振动行为、减振优化设计等问题,基于各向异性弹性理论、层合板理论、非线性弹性板理论、von Karman理论和Reddy三阶剪切变形理论,采用解析推导、数值仿真与实验测试相结合的方法,面向工程中薄板结构的减振需求,进行系统的学理研究,其主要研究工作与相关科学结论如下。 【研究1】 基于纳米压痕实验,以电子束物理气相沉积(EB-PVD)制备的NiCrAlY硬涂层为代表,通过各向同性弹性体(Isotropic Elastic Body)和各向异性弹性体(Anisotropic Elastic Body)设定,结合有限元模拟,辨识其力学特性参数。 将硬涂层简化为各向同性弹性材料,以弹性各向同性涂层-基体复合结构压痕过程的加载曲线为出发点,通过无量纲分析和有限元模拟,结合纳米压痕实验得到的加载曲线,求解了虑及基体效应的涂层材料弹性模量。 针对各向异性的硬涂层-基体复合结构,通过简化硬涂层本构关系模型,确定了独立力学特性参数ET和EL;应用无量纲分析和有限元模拟,得到了压痕响应过程中的最大加载力、加载曲线指数与硬涂层力学特性参数ET和EL之间的无量纲方程;结合纳米压痕实验,得到了横观各向同性材料参数。 【结论1】 辨识出EB-PVD制备的NiCrAlY涂层的等效各向同性弹性模量,以及各向异性的力学特性参数(见表33)。 【Conclusion 1】 Equivalent isotropic and anisotropic elastic modulus of NiCrAlY coating deposited by EB-PVD obtained in this paper are listed in Tab.33. 表33 辨识到的EB-PVD制备NiCrAlY涂层的材料参数Tab.33 Material parameters of NiCrAlY coating prepared by EB-PVD 【研究2】 虑及涂层的各向异性力学特性,采用数值方法和实验测试,分析了涂层-薄板复合结构的振动特性;建立了涂层-薄板复合结构有限元模型,通过代入涂层各向异性材料参数,分析了涂敷NiCrAlY涂层的悬臂钛板的固有特性;通过施加加速度基础激励计算了共振状态下的响应;采用振动台对悬臂涂层板进行基础激励,从瀑布图中辨识出了前8阶固有频率;采用半功率带宽法计算出前8阶模态阻尼比,测试了基础激励下的振动响应。 【结论2】 通过对比采用辨识方法得到的各向同性材料参数,以及由横观各向同性材料参数计算,得到固有频率与实验测试结果的差异率,发现横观各向同性材料参数的结果在高阶部分(4~8阶)与实验测试得到的结果更为接近(差异均在2%以内)。说明:在进行硬涂层结构的高阶振动特性分析以及硬涂层对高周疲劳抑制研究时,应当采用横观各向同性的本构关系。 【Conclusion 2】 Comparision between the natural frequencies calculated by using of isotropic and transversely isotropic material parameters and experimental results reveals that, at high-order modes, results of transversely isotropic material parameters are closer to experimental results with a difference ratio of 2%. This demonstrated that transversely isotropic constitutive relation should be adopted when studying high-order vibration characteristics and high-cycle fatigue suppression of hard coating structure. 【研究3】 采用数值计算方法与实验测试方法,通过对比涂层前后悬臂钛板减振指标(固有频率、阻尼比、共振位移响应、最大应力值和疲劳寿命等)的变化,综合评价了悬臂钛板涂敷NiCrAlY涂层的减振有效性。 【结论3】 硬涂层具有良好的阻尼减振能力。涂敷NiCrAlY涂层后,悬臂钛合金板的前10阶固有频率增大1.600%~1.972%;前8阶模态阻尼比,除第3阶略有降低、第5阶基本不变外,其他各阶上升15.79%~160%,表明:涂敷NiCrAlY涂层之后,能量耗散增大;容易引起悬臂钛板疲劳破坏的第4阶及第10阶模态,共振状态下振动幅值及振动应力明显下降;第4阶共振态下悬臂钛板的共振疲劳寿命明显上升。 【Conclusion 3】 Hard coating has sound damping capacity. After depositing NiCrAlY coating, the first 10 natural frequencies increase by 1.600%~1.972%, while the first 8 order damping ratios increase by 15.79%~160% except the 3rdand 5thorder. It reveals that energy disspation is promoted after depositing NiCrAlY coating. For the 4thand 10thmodes which are more likely to induce fatigue failure of cantilivered plate, vibration amplitude and stress reduce evidently. Fatigue life under the 4thorder resonace is improved significantly. 【研究4】 基于非线性薄板理论,采用Galerkin法及小参数法,计算了由各向异性硬涂层材料和各向同性金属材料组成的硬涂层-薄板复合结构(CP-Structure)非线性动力特性;虑及复合材料悬臂板的几何关系非线性和材料非线性,建立了硬涂层-薄板非线性运动方程(NDEHCTP);采用Galerkin法将NDEHCTP转化为非线性常微分方程,采用小参数法将其展成为线性微分方程进行求解,获得了悬臂硬涂层-薄板非线性动力特性的近似解析解;运用有限元法和实验测试法比较和验证了解析解。 【结论4】 通过对3个不同尺寸,不同涂层材料的悬臂硬涂层-薄板固有频率的计算,发现非线性解析方法和有限元方法所求得的固有频率以及实验测试的结果都十分贴近(最大差异9.47%),而线性解析方法求得的固有频率在3阶以后相差的比较大(最大差异17.59%)。说明:CP-Structure的高阶振动特性分析,采用非线性弹性板理论更能比较精确的计算。 【Conclusion 4】 Natural frequencies obtained by nonlinear analytical method and finite element method are close to the experimental results with the maximum difference ratio of 9.47%. However, results obtained by linear analytical method differ from the experimental results by the maximum difference ratio of 17.59% after the 3rdmode.So we can make a conclusion that nonlinear elastic plate theory can get more precise results of analysis in high-order vibration of CP-Structure. 【研究5】 建立了在受横向载荷作用下悬臂硬涂层-薄板的动力学方程;基于板的von Karman理论以及Reddy三阶剪切变形理论(RTOSDTP),虑及横向外阻尼的影响,运用Haimilton原理推导出悬臂硬涂层-薄板非线性动力学方程(NDEHCTP);运用Galerkin法对悬臂硬涂层-薄板偏微分方程进行离散,得到硬涂层-薄板横向变形非线性控制方程(NGELD);以悬臂钛合金薄板和悬臂硬涂层-薄板为研究对象,实验研究了其在横向谐波激励作用下的动态响应。 【结论5】 非共振区间激振频率的变化对于钛合金薄板振动响应形态有以下影响:当激振频率Ω在30~2 200 Hz作正向激励时,随着Ω的增大,薄板将出现“多周期运动→四倍周期运动→单倍周期运动→混沌运动→二倍周期运动→混沌运动→多周期运动→单倍周期运动→混沌运动”,并在Ω=770~790 Hz区间,引发板的1∶2内共振。 【Conclusion 5】 When the off-resonance frequencies vary among the range from 30Hz to 2200Hz, the vibration behavior of thin plate changes by multicycle motion→quadruple period motion→haplotype period motion→chaos motion→double period motion→ chaos motion→multicycle motion→haplotype period motion→chaos motion. 【结论6】 非共振区间激振频率的变化对于硬涂层-薄板的振动响应形态有以下影响:激振频率Ω在30~2 200 Hz作正向激励时,随着Ω的增大,薄板将出现“多周期运动→四倍周期运动和三倍周期运动交替→单倍周期运动→混沌运动→多周期运动和混沌运动交替→多周期运动”。 【Conclusion 6】 When the off-resonance frequencies vary among the range from 30 Hz to 2200Hz, the vibration behavior of CP-Structure changes by multicycle motion→alternation of quadruple and triple period motion→haplotype period motion→chaos motion→ alternation of multicycle motion and chaos motion→multicycle motion. 【结论7】 硬涂层-薄板比钛合金薄板的振动形态要复杂:140~440 Hz和720~1 110 Hz时,硬涂层-薄板的响应表现为多种振动形态的交替出现。但是,硬涂层-薄板发生混沌运动的区间要比钛合金薄板小,尤其是在高频率范围(1 770~2 200 Hz),硬涂层抑制了混沌运动的发生。 【Conclusion 7】 Vibration behavior of CP- Structure are more complex than what of thin plate because alternation of two motion kinds appears at 140~440 Hz and 720~1 110 Hz. However, chaos motion is suppressed by hard coating at high frequency range(1 770~2 200 Hz). 【结论8】 悬臂钛合金薄板和悬臂硬涂层-薄板的主共振响应表明:硬涂层-薄板响应的振幅明显小于钛合金薄板;钛合金薄板和硬涂层-薄板的共振区实测幅频响应振幅表明,第5阶以及更高阶次的钛合金薄板的振幅是硬涂层-薄板的3~15倍。硬涂层具有优秀的减振效果。 【Conclusion 8】 Principal resonance response of cantilevered thin plate and CP-Structure shows that response amplitudes of CP-Structure are obviously lower than that of thin plate. The 5thand higher order resonance amplitude of thin plate are 3~15 times of the counterpart. All these demonstrate the good damping effect of hard coating. 【研究6】 以提高复合结构强度和显著提高结构系统阻尼特性为目标,建立了以Etanδ最大化为核心的涂层阻尼减振优化设计组合性能指标体系,创立了硬涂层-薄板结构阻尼减振的优化设计方法;建立了基于Reuss模型的复合结构力学特性计算模型(MMCSBRM),规划出包括硬涂层厚度hC,硬涂层弹性模量EC和硬涂层损耗因子ηC的设计变量体系;确定了上述参数的约束条件,给出了硬涂层阻尼减振的优化设计流程(ODPBRM);以钛合金薄板为例进行了硬涂层阻尼减振优化设计实例验证。 以某钛合金薄板为实例,采用优化流程对硬涂层的弹性模量、损耗因子以及涂敷厚度进行了寻优,讨论了上述参数对复合结构系统力学特性的贡献,得出了以下结论。 【结论10】 涂层损耗因子tanδC越大,越有助于提高组合性能指标Etanδ及减振能力指标tanδ,而且在所研究的0~0.1范围内,增长幅度可近似为一种线性关系。因而在涂层材料选取时应该尽量选择具有较大阻尼特性的材料,在制备过程中通过工艺优化形成较强阻尼能力的涂层。 【Conclusion 10】 The higher loss factor of coating tanδC, the more beneficial toEtanδand tanδ. Besides, the increasing amplification shows a linear relationship betweenEtanδand tanδCin the range of 0~0.1. So material with large damping capacity should be selected and the deposition process should be optimized in order to get the hard coating with high damping capacity. 【结论12】 在基体厚度为3 mm的钛板上涂敷300 μm涂层后,发生了频率偏移(增加2.49%~2.70%)、模态阻尼比显著增加(增加13.62%~16.82%)、谐响应共振峰显著降低(降低90%以上)等现象,证实了减振优化设计的明显效果。 【Conclusion 12】 After depositing hard coating with thickness of 300 μm, the natural frequency of Titanium plate is enlarged by 2.49%~2.70%, the modal damping ratio is enlarged by 13.62%~16.82% and the resonance peak decreases 90%. All these demonstrate the beneficial effect of damping optimazation. 8.2 展望 由于硬涂层减振属于新兴研究方向,其力学特性的准确表征和测试、减振机理与有效性、合理动力学模型的建立,以及基于合理动力学模型的计算、非线性振动行为等尚处于探索阶段,在今后工作中,可以考虑从以下方面继续开展工作: (1)将硬涂层考虑为更一般的各向异性材料,得出其全部弹性系数矩阵,更准确地表达其各向异性的力学特性。 (2)涂层与基体的界面关系对于涂层复合结构振动特性以及涂层减振效果的影响,还需要进一步研究。 (3)由于涂层特别薄,涂层材料力学参数的各向异性特征以及非线性特征对涂层-基体复合结构振动特性的影响在本文中并不明显,今后还需要进行进一步研究与探索硬涂层的这些特征对于涂层复合结构振动特性以及涂层减振效果的影响规律,以便进行主动优化设计。 (4)本文中计算的涂层前后悬臂钛板的振动疲劳寿命,只能从直观上比较硬涂层的减振效果,其具体数值会受到其他诸多因素的影响,因而数据的可信性还有待于进一步实验验证。 (5)从目前研究来看,尽管硬涂层的阻尼能力比常见的有机高分子涂层相对较低,但硬涂层还同时具有能够承受高温环境、改善表面质量、抵抗外物磨损等特性。所以,进一步开展多功能硬涂层技术研究对于高端旋转机械中的关键结构件更具有特殊意义。 (6)硬涂层减振机理特别是其阻尼机制十分复杂,如果能够从微观、介观以及宏观等不同层次对硬涂层复合结构进行多尺度研究,将有可能实现硬涂层结构的阻尼和强度等多目标优化,并能保证实现复合结构预期的力学、机械性能与动力学特征。 [1] 徐滨士,朱绍华,刘世参,等.表面工程.北京:机械工业出版社,2000,35-37. Xu Binshi,Zhu Shaohua,Liu Shican,etal.Surface Engineering.Beijing:China Machine Press,2000,35-37. [2] 夏光明,周建桥,闵小兵,等.涂层技术概述及工程应用.金属材料与冶金工程,2012,40(1):53-59. Xia Guangming,Zhou Jianqiao,Min Xiaobing,etal.Overview on Coating Technology and its Engineering Application. Metal Materials and Metallurgy Engineering,2012,40(1):53-59. [3] Pawlowski L.The Science and Engineering of Thermal Spray Coatings.England,UK:John Wiley & Sons Ltd.,1995. [4] Blackwell C,Palazotto A,George T J,etal.The Evaluation of the Damping Characteristics of a hard Coating on Titanium.Shock and Vibration,2007,14(1):37-51. [5] Movchan B A,Ustinov A I.Highly Damping hard Coatings for Protection of Titanium Blades//In Evaluation, Control and Prevention of high Cycle Fatigue in Gas Turbine Engines for Land,Sea and Air Vehicles//Meeting Proceedings RTO-MP-AVT-121,2005,Paper 11:1-16. [6] Janet McGovern.Advanced Blade-Damping Coatings.Navy SBIR,2006(2):Topic N06-118. [7] Kolkman H.Effect of TiN/Ti Gas Turbine Compressor Coatings on the Fatigue Strength of Ti-6Al-4V Base Metal.Surface and Coatings Technology,1995,72(1):30-36. [8] Chia C,Khor K,Gu Y,etal.Viscoelastic Properties of Plasma Sprayed NiCoCrAlY Coatings.Thin Solid Films,2002,405(1):146-152. [9] Wang B,Gong J,Wang A Y,etal.Oxidation Behaviour of NiCrAlY Coatings on Ni-Based Superalloy.Surface and Coatings Technology,2002,149(1):70-75. [10] Easterday O T.An Experimental Characterization of Damping Properties of Thermal Barrier Coatings at Elevated Temperatures[Ph.D Thesis].USA,Ohio:Air Force Institute of Technology,2011. [11] Jang B-K,Matsubara H.Influence of Porosity on Hardness and Young's Modulus of Nanoporous EB-PVD TBCs by Nanoindentation.Materials Letters,2005,59(27):3462-3466. [12] Tassini N,Lambrinou K,Mircea I,etal.Study of the Amplitude-Dependent Mechanical Behaviour of Yttria-Stabilised Zirconia Thermal Barrier Coatings.Journal of the European Ceramic Society,2007,27(2): 1487-1491. [13] Locatelli M R,Fuller Jr E R.Using OOF to Model Mechanical Behavior of Thermal Barrier Coatings//Proceedings of the Symposium on Advanced Ceramic Coatings International,Conference on Advanced Ceramic and Composites,2002. [14] Torvik P J.Determination of Mechanical Properties of non-Linear Coatings from Measurements with Coated Beams.International Journal of Solids and Structures,2009,46(5):1066-1077. [15] Torvik P J.On Estimating System Damping from Frequency Response Bandwidths.Journal of Sound and Vibration,2011,330(25):6088-6097. [16] Torvik P,Patsias S,Tomlinson G.Characterising the Damping Behaviour of hard Coatings:Comparisons from two Methodologies//Proceedings of the 6th National Turbine Engine High Cycle Fatigue (HCF) Conference,2002. [17] Green J,Patsias S.A Preliminary Approach for the Modeling of a hard Damping Coating Using Friction Elements//7th National Turbine Engine high Cycle Fatigue Conference,2002. [18] Yu L,Ma Y,Zhou C,etal.Damping Capacity and Dynamic Mechanical Characteristics of the Plasma-Sprayed Coatings.Materials Science and Engineering(A),2005,407(1):174-179. [19] Patsias S,Tomlinson G R,Jones M A.Initial Studies into hard Coatings for Fan Blade Damping//Rolls Royce PLC-REPORT-PNR,2001. [20] Ivancic F T.The Effect of a hard Coating of the Damping and Fatigue Life of Titanium[Ph.D Thesis].Ohio:Air Force Institute of Technology,2003. [21] 李行志.等离子喷涂涂层的工艺、组织与性能研究[博士学位论文].武汉:武汉科技大学,2004. Li Xingzhi.Study on the Process,Microstructure and Property of Plasma Sprayed Coatings[Ph.D Thesis].Wuhan:Wuhan University of Science and Technology,2004. [22] Leissa A W.The free Vibration of Rectangular Plates.Journal of Sound and Vibration,1973,31(3):257-293. [23] Gorman D J.Free Vibration Analysis of Cantilever Plates by the Method of Superposition.Journal of Sound and Vibration,1976,49(4):453-467. [24] Gorman D J.Accurate free Vibration Analysis of the Orthotropic Cantilever Plate.Journal of Sound and Vibration,1995,181(4):605-618. [25] Hirai T,Chen L.Recent and Prospective Development of Functionally Graded Materials in Japan.Master Sci. Forum,1999,308:509-514. [26] Chen W Q,Ding H J.Bending of Functionally Graded Piezoelectric Rectangular Plates.Acta Mech Solida Sinica,2000,13(4):312-319. [27] Cheng Z Q,Lim C W,Kitipornchai S.Three-Dimensional Asymptotic Approach to Inhomogeneous and Laminated Piezoelectric Plates.International Journal of Solids and Structures,2000,37:3153-3175. [28] Lim C W,He L H.Exact Solution of a Compositionally Graded Piezoelectric Layer under Uniform Stretch, Bending and Twisting.Int. J. Mech. Sci.,2001,43:2479-2492. [29] Yen H Y,Herman Shen M H.Passive Vibration Suppression of Beams and Blades Using Magnetomechanical Coating.Journal of Sound and Vibration,2001,245(4):701-714. [30] Reddy J N.An Overview of the Relationships Between Solutions of the Classical and Shear Deformationplate Theories.Composites Science and Technology,2000,60:2327-2335. [31] Reddy J N.Mechanics of Laminated Composite Plates and Shells:Theory and Analysis.Boca Raton:CRC Press,2004. [32] Reddy J N.Analysis of Laminated Adaptive Plate Structures Using Layerwise Finite Element Models.Computers and Structures,2004,82(23):1939-1959. [33] Shih Y S,Blotter P T.Non-Linear Vibration Analysis of Arbitrarily Laminated thin Rectangular Plates on the Elastic Foundation.Journal of Sound and Vibration,1993,167(3):433-459. [34] Han W,Petyt M.Geometrically Nonlinear Vibration Analysis of Thin,Rectangular Plates Using the Hierarchical Finite Element Method I:the Fundamental Mode of Isotropic Plates.Computers & Structures,1997,63(2):295-308. [35] Turkmen H S,Mecitoglu Z.Nonlinear Structural Response of Laminated Composite Plates Subjected to Blast Loading.AIAA J,1999 37(12):1639-1647. [36] Turkmen H S.Structural Response of Cylindrically Curved Laminated Composite Shells Subjected to Blast Loading. Int. J. Phys. Eng. Sci.(ARI),1999 51(3):175-180. [37] Turkmen H S.Structural Response of Laminated Composite Shells Subjected to Blast Loading:Lomparison of Experimental and Theoretical Methods.Journal of Sound and Vibration,2002,249(4):663-678. [38] Zhang W.Global and Chaotic Dynamics for a Parametrically Excited thin Plate.Journal of Sound and Vibration,2001,239(5):1013-1036. [39] 郝五零,张 伟.参数激励和外激励联合作用下薄板的非线性动力学.动力学与控制学报,2014 (2):139-146. Hao Wuling,Zhang Wei.Nonlinear Dynamics of a Parametrically and Externally Excited Thin Plate.Journal of Dynamics and Control,2014(2):139-146. [40] Yu P,Zhang W,Bi Q S.Vibration Analysis on a thin Plate with the Aid of Computation of Normal Forms.International Journal of Non-Linear Mechanics,2001,36(4):597-627. [41] 姚明辉,张 伟.含参数激励的薄板的多脉冲轨道和混沌动力学分析//首届航空航天力学会议论文集,成都,2004:299-301. Yao Minghui,Zhang Wei.Many Pulses Heteroclinic Orbits and Chaotic Dynamics Analysis of a Parametrically and Externally Excited thin Plate//The First Conference on Mechanics of Aeronautics and Astronautics,Chengdu,2004:299-301. [42] Yao M H,Zhang W,Fan J H.Many Pulses Heteroclinic Orbits with a Melnikov Method and Chaotic Dynamics of a Parametrically and Externally Excited thin Plate//The Second International Conference on Dynamics,Vibration and Control,Beijing,China,2006. [43] Zhang J H,Zhang W.Global Bifurcation and Chaotic Dynamics for a non-Autonomous Buckled thin Plate.Journal of Dalian University of Technology,2006,46:1-6. [44] Zhang J H,Zhang W,Yao M H.Global Dynamics for a non-Autonomous Buckled Thin Plate with Parametrically and Externally Excitations//Proceedings of the Fifth International Conference on nonlinear Mechanics,Shanghai,China,2007. [45] Yao M H,Zhang W.Multi-Pulse Shilnikov Orbits and Chaotic Dynamics of a Parametrically and Externally Excited thin Plate.International Journal of Bifurcations and Chaos,2007,17:1-25. [46] Zhang W,Zhang J H,Yao M H.Multi-Pulse Chaotic Motion for a Non-Autonomous Buckled Plate by Using the Extended Melnikov Method//Proceedings of the ASME 2007 International Mechanical Engineering Conferences and Exposition,Seattle,Washington,USA,2007,11-15. [47] 姚明辉,张 伟.利用广义Melnikov方法研究薄板的多脉冲混沌运动//第八届全国非线性动力学和运动稳定性学术会议论文集,石家庄,2007:1-5. Yao Minghui,Zhang Wei.Analysis with a Generalized Melnikov Method for Multi-pulse Chaotic Movement of thin Plate//The 8th Chinese Conference on Nonlinear Dynamics and Kinetic Stability,Shijiazhuang,2007:1-5. [48] Cole S R.Effects of Spoiler Surfaces on the Aero Elastic Behavior of a low-Aspect-Ratio Rectangular Wing.AIAA Paper 90-0981. [49] Kung G C,Pao Y H.Nonlinear Flexural Vibrations of a Clamped Circular Plate.Journal of Applied Mechanics,1972,39(4):1050-1054. [50] Nayfeh A H,Mook D T.Nonlinear Oscillations.New York:John Wiley & Sons,1979. [51] Chia C Y.Nonlinear Analysis of Plates.New York:McGraw-Hill,1980. [52] Sathyamoorthy M.Nonlinear Analysis of Structures.New York:CRC Press,1997. [53] Nayfeh A H.Nonlinear Interactions.New York:John Wiley & Sons,2000. [54] Yamaki N,Chiba M.Nonlinear Vibrations of a Clamped Rectangular Plate with Initial Deflection and Initial Edge Displacement V Part I:Theory.Thin-Walled Structures,1983,1:3-29. [55] Yamaki N,Otomo K,Chiba M.Nonlinear Vibrations of a Clamped Rectangular Plate with Initial Deflection and Initial Edge Displacement V Part II:Experiment,Thin-Walled Structures.1983,1:101-119. [56] Oh K.A Theoretical and Experimental Study of Modal Interactions in Metallic and Laminated Composite Plates[Ph.D Thesis].Blacksburg,Virginia:Virginia Polytechnic Institute and State University,1994. [57] Oh K,Nayfeh A H.High-to low-Frequency Modal Interactions in a Cantilever Composite Plate.Journal of Vibration and Acoustics,1998,120:579-587. [58] Amabili M,Carra S.Experiments and Simulations for Large-Amplitude Vibrations of Rectangular Plates Carrying Concentrated Masses.Journal of Sound and Vibration,2012,331:155-166. [59] Kim T,Kim J.Eigensensitivity Based Optimal Distribution of a Viscoelastic Damping Layer for a Flexible Beam.Journal of Sound and Vibration,2004,273(1):201-218. [60] Kumar N,Singh S P.Experimental Study on Vibration and Aamping of Curved Panel Treated with Constrained Viscoelastic Layer.Composite Structures,2010,92(2):233-243. [61] Zheng H,Cai C,Tan X M.Optimization of Partial Constrained Layer Damping Treatment for Vibrational Energy Minimization of Vibrating Beams.Computers and Structures,2004,82 (29):2493-2507. [62] Zhao M,Chen X,Xiang Y,etal.Measuring Elastoplastic Properties of thin Films on an Elastic Substrate Using Sharp Indentation.Acta Materialia,2007,55(18):6260-6274. [63] Tunvisut K,O'Dowd N P,Busso E P.Use of Scaling Functions to Determine Mechanical Properties of thin Coatings from Microindentation Tests.International Journal of Solids and Structures,2001,38(2):335-351. [64] Bolshakov A,Pharr G.Influences of Pileup on the Measurement of Mechanical Properties by Load and Depth Sensing Indentation Techniques.Journal of Materials Research,1998,13(4):1049-1058. [65] Oliver W C,Pharr G M.Improved Technique for Determining Hardness and Elastic Modulus Using Load and Displacement Sensing Indentation Experiments.Journal of Materials Research,1992,7(6):1564-1583. [66] Sneddon I N.The Relation Between Load and Penetration in the Axisymmetric Boussinesq Problem for a Punch of Arbitrary Profile.International Journal of Engineering Science,1965,3(1):47-57. [67] 周益春.材料固体力学.北京:科学出版社,2006. Zhou Yichun.Solid Mechanics in Materials.Beijing:Science Press,2006. [68] Standard ASTM.Standard Test Method for Determination of Reference Temperature for Ferritic Steels in the Transition Range.Annual Book of ASTM Standards,1921. [69] Lima R,Kruger S,Marple B.Towards Engineering Isotropic Behaviour of Mechanical Properties in Thermally Sprayed Ceramic Coatings.Surface and Coatings Technology,2008,202(15):3643-3652. [70] Wang J,Zheng X,Zheng H,etal.Identification of Elastic Parameters of Transversely Isotropic thin Films by Combining Nanoindentation and FEM Analysis.Computational Materials Science,2010,49(2):378-385. [71] Nakamura T,Gu Y.Identification of Elastic-Plastic Anisotropic Parameters Using Instrumented Indentation and Inverse Analysis.Mechanics of Materials,2007,39(4):340-356. [72] Vlass J J,Ciavarella M,Barber J,etal.The Indentation Modulus of Elastically Anisotropic Materials for Indenters of Arbitrary Shape.Journal of the Mechanics and Physics of Solids,2003,51(9):1701-1721. [73] Vlass J J,Nix W.Measuring the Elastic Properties of Anisotropic Materials by Means of Indentation Experiments.Journal of the Mechanics and Physics of Solids,1994,42(8):1223-1245. [74] Hibbitt Karlsson & Sorensen Inc..Abaqus/CAE User's Manual.America:HKS Inc.,2002. [75] Jablokov V R,Murray N G,Rack H J,etal.Influence of Oxygen Content on the Mechanical Properties of Titanium-35 Niobium-7 Zirconium-5 Tantalum Beta Titanium Alloy.Titanium,Niobium,Zirconium,and Tantalum for Medical and Surgical Applications,2006,2(1471):40. [76] Kerans R,Hay R,Pagano N,etal.The Role of the Fiber-Matrix Interface in Ceramic Composites.American Ceramic Society Bulletin,1989,68:429-442. [77] 张建华,张勤俭,张勤河,等.沉积偏压对电弧离子镀TiN涂层质量的影响//2001 年中国机械工程学会年会暨第九届全国特种加工学术年会论文集,苏州,2001:380-382. Zhang Jianhua,Zhang Qinjian,Zhang Qinhe,etal.Effect of Deposition Bias Voltage on Quality of Arc Ion Plating TiN Coating//2001 Mechanical Engineering Society Annual Meeting of China & the 9thAcademic Annual Conference on Non-traditional Machining,Suzhou,2001:380-382. [78] 柴 山,吕凤军,孙义冈,等.计算汽轮机叶片动应力的谐响应分析法.汽轮机技术,2002,44(5):267-268. Chai Shan,Lv Fengjun,Sun Yigang,etal.Computation for Dynamic Stress of Steam Turbine Blade by Using the Method of Harmonic Response Analysis.Turbine Technology,2002,44(5):267-268. [79] 王 婧,王德友,韩清凯.压气机叶片掉角故障的机理分析及其治理.中国机械工程,2008,19(9): 1048-1050. Wang Jing,Wang Deyou,Han Qingkai.Mechanism Analysis and Treatment on Loss Corner Faults of Compressor Blades.Chinese Journal of Mechanical Engineering,2008,19(9):1048-1050. [80] 可成河,巩孟祥,赵 鑫.某型发动机高压压气机第 6 级静子叶片掉角故障分析.航空发动机,2012,38(2):55-58. Ke Chenghe,Gong Mengxiang,Zhao Xin.Fracture Failure Analysis of Six-Stage Stator Blade for an Areoengine HP Compressor.Aeroengine,2012,38(2):55-58. [81] 胡晓阳.浅谈金属材料疲劳断裂现象及在生产中的应用.机械管理开发,2011(5):93-94. Hu Xiaoyang.On the Fatigue Fracture of Metal and its Application in Production.Mechanical Management and Development,2011(5):93-94. [82] 尹泽勇,主编.航空发动机设计手册(第18册).北京:航空工业出版社,2001. Yin Zeyong,editor-in-chief.Design Manual for Aircraft Engine(18th vol.).Beijing:Aviation Industry Press,2001. [83] Yang J,Chen H S.Dynamic Response of Initially Stressed Functionally Graded Rectanglar thin Plates.Composite Struct,2001,54:497-508. [84] 何福保,沈亚鹏.板壳理论.西安:西安交通大学出版社,1993. He Fubao,Shen Yapeng.Theory of Plates and Shells.Xi’an:Xi'an Jiaotong University Press,1993. [85] 曹志远.功能梯度板的非线性动力分析,固体力学学报,2006,27(1):21-25. Cao Zhiyuan.Nonlinear Dynamic Analysis of Functionally Graded Material Plates.Acta Mechanica Solida Sinica,2006,27(1):21-25. [86] Pai P F,Nayfeh A H.A Refined Nonlinear Model of Composite Plates with Integrated Piezoelectric Actuators and Sensors.International Journal of Solids and Structures,1993,30(12):1603-1630. [87] Lakes R S.High Damping Composite Materials:Effect of Structural Hierarchy.Journal of Composite Materials,2002,36(3):287-297. [88] Brodt M,Lakes R S.Composite Materials which Exhibit high Stiffness and high Viscoelastic Damping.J. Composite Materials,1995,29:1823-1833. [89] Patsias S,Saxton C,Shipton M.Hard Damping Coatings:an Experimental Procedure for Extraction of Damping Characteristics and Modulus of Elasticity.Materials Science and Engineering,2004,370(1):412-416. * 中国国家重点基础发展计划(973计划)项目《高端压缩机组高效可靠及智能化基础研究》(No.2012CB026000)和《硬岩掘进装备的关键技术问题》(No.2013CB035402),中国国家自然科学基金资助项目《薄壁构件硬涂层阻尼减振的多尺度模拟方法与主动设计》(No.11472068)和《弹性支承多转子系统的不对中建模与振动分析》(No.51175070),中央高校基本科研业务费专项资金资助项目《硬涂层薄板复合结构的减振机理及振动疲劳特性研究》(No.858029)







8 结论与总结